좌익수

컴퓨터 과학에서 좌익 트리 또는 좌익 힙은 이진 힙의 변형으로 구현되는 우선 순위 대기열이다.모든 노드 x에는 x에 뿌리를 둔 하위 트리에서 가장 가까운 리프까지의 거리인 s-값이 있다.^[1]이항 힙과는 대조적으로 좌익 트리는 매우 불균형을 시도한다.힙 속성 외에도 좌익 트리가 유지되기 때문에 각 노드의 오른쪽 후예가 더 낮은 s-값을 갖는다.

높이 편향된 좌익 나무는 클라크 알란 크레인에 의해 발명되었다.^[2]그 이름은 왼쪽 하위 트리가 보통 오른쪽 하위 트리보다 키가 크다는 사실에서 유래되었다.

왼쪽 나무는 병합할 수 있는 더미다.트리에 새 노드를 삽입하면 새로운 1노드 트리가 생성되어 기존 트리에 병합된다.항목을 삭제하려면 왼쪽과 오른쪽 하위 트리의 병합으로 대체한다.이 두 작업 모두 O(log n) 시간이 걸린다.삽입의 경우 이는 O(1) 상각 시간(정수) 및 O(log n) 최악의 경우 삽입을 지원하는 피보나치 힙보다 느리다.

좌익수들은 Ⅱ(n)가 걸리는 2진 무더기에 비해 빠르게 융합할 수 있는 능력이 뛰어나기 때문에 유리하다.거의 모든 경우에서, 꼬치잡이의 합치는 성능이 더 좋다.그러나 좌익 힙합을 합병하면 O(log n) 복잡성이 가장 심하고, 꼬치 힙을 합병하면 O(log n) 복잡성이 상각된다.

바이어스

흔히 볼 수 있는 좌파 나무는 키에 치우친 좌파 나무다.^[2]그러나 무게 편향 좌익 나무에서와 같이 다른 편견이 존재할 수 있다.^[3]

S-값

좌익수 S-값

노드의 s-값(또는 순위)은 해당 노드에서 해당 노드에 뿌리를 둔 하위 트리에서 가장 가까운 리프까지의 거리를 의미한다.다른 방법으로, a의 s-값null아이는 암묵적으로 0이다.다른 노드의 s-값은 자식 값의 최소 하나 이상과 동일하다.따라서 오른쪽 예제에서 하나 이상의 누락된 자식을 가진 모든 노드의 s-값은 1인 반면, 노드 4의 s-값은 2인 반면, 오른쪽 자식(8)의 s-값은 1이므로(일부 설명에서 null childs의 s-값은 -1인 것으로 가정한다.)^[4]

x에 뿌리를 둔 하위 트리에서 가장 가까운 누락된 잎에 대한 최단 경로를 아는 것은 정확히 s(x)이며, s(x)-1 이하의 모든 노드는 s(x)가 그렇지 않았다면 더 적을 것이기 때문에 정확히 2명의 자식을 가지고 있다.x에 뿌리를 둔 트리의 크기가 최소 ${\displaystyle {2초(x}^{}}$)${\displaystyle {}^{}}$- ${\displaystyle 1}$ ${\displaystyle$ 2$^{s(x)}-1$ 따라서 s(x)는 최대 log${\displaystyle \log }$ (${\displaystyle \mathrm{m}}$+${\displaystyle 1}$ )${\$)},$$m은 x에 뿌리를 둔 하위 트리의 노드 수입니다.^[1]

높이 편향 좌익수^[1] 작업

높이 편향 좌익 나무의 대부분의 작업은 병합 작업을 사용하여 이루어진다.

두 개의 최소 HBLT 병합

병합 작업은 두 개의 Min HBLT를 입력으로 사용하고 원래 Min HBLT에 있는 모든 노드를 포함하는 Min HBLT를 반환한다.

A 또는 B 중 하나가 비어 있으면 병합이 다른 하나를 반환한다.

Min HBLTs의 경우, A.key $\le {\displaystyle }$ ${\displaystyle \leq$}B$$.key가 있는 A와 B.key에 두 개의 나무가 뿌리를 두고 있다고 가정해 보십시오.그렇지 않으면 위의 조건이 유지되도록 A와 B를 교환할 수 있다.

병합은 A의 오른쪽 하위 트리와 B를 병합하여 재귀적으로 이루어진다.이것은 A의 오른쪽 하위 트리의 S-값을 변화시킬 수 있다.왼쪽 트리 속성을 유지하기 위해 각 병합이 완료된 후 재귀적 병합 호출 시 오른쪽 하위 트리의 S-값이 왼쪽 하위 트리의 S-값보다 커졌는지를 확인한다.그렇다면 오른쪽과 왼쪽 하위 트리를 교환한다(한 명의 아이가 없어지면 오른쪽이 되어야 한다).

A의 뿌리가 B의 뿌리보다 크다고 가정했기 때문에 힙 속성도 유지된다.

2분 높이의 편향 좌익수 합성을 위한 유사점

MERGE(A, B)만약 A=null반환 B만약 B)null 돌아온 만약 A.key >, B.key 반환 MERGE(B, A)A.right:)MERGE(A.right, B)// 그 결과가 될 수 없다가 null이 이후 B가 null이 아닌 만약 A.left) 빈 다음 SWAP(A.left, A.right)A.s_value:=1을 끓여이후 오른쪽 종속 트리가 null가장 짧은 경로에 서브 잎으로부터 노드 A 는1 A가 맞으면 A를 반환한다.s_value > A.left.s_value 다음에 SWAP(A.right, A.left) A.s_value := A.right.s_값 + 1 리턴 A

Java 코드: 2분 높이의 편향된 좌익 트리 병합

공중의 노드 합병하다(노드 x, 노드 y) {     만일 (x == 무효의)         돌아오다 y;     만일 (y == 무효의)          돌아오다 x;      // 만약 이것이 최대치였다면,     // 다음 행은 다음과 같다: (x.csv < y.csv)     만일 (x.요소.비교(y.요소) > 0)         // x.198 > y.1987         돌아오다 합병하다 (y, x);      x.우차일드 = 합병하다(x.우차일드, y);      만일 (x.좌차일드 == 무효의) {         // 왼쪽 아이가 없으므로 오른쪽 아이를 왼쪽으로 이동하십시오.         x.좌차일드 = x.우차일드;         x.우차일드 = 무효의;         // x.s는 1이었다.     } 다른 {         // 왼쪽 아이가 존재하기 때문에 s-multi를 비교하십시오.         만일 (x.좌차일드.s < x.우차일드.s) {             노드 임시 변통하다 = x.좌차일드;             x.좌차일드 = x.우차일드;             x.우차일드 = 임시 변통하다;         }         // 우리는 적절한 아이가 낮은 s-값을 가지고 있다는 것을 알기 때문에, 우리는 단지         // s-값에 하나를 추가         x.s = x.우차일드.s + 1;     }     돌아오다 x; } 

해스켈 코드: 2분 높이의 편향된 좌익 나무 병합

자료 LHeap a   = 잎     노드 a (LHeap a) (LHeap a)  등수를 매기다 :: LHeap a -> 정수 등수를 매기다 잎 = 0 등수를 매기다 (노드 _ _ r) = 등수를 매기다 r + 1  합병하다 :: 서드 a => LHeap a -> LHeap a -> LHeap a 합병하다 잎 h = h 합병하다 h 잎 = h 합병하다 h@(노드 a l r) h'@(노드 a의 _ _)     a > a의           = 합병하다 h' h     등수를 매기다 r' > 등수를 매기다 l = 노드 a r' l     그렇지 않으면        = 노드 a l r'   어디에 r' = 합병하다 r h' 

예

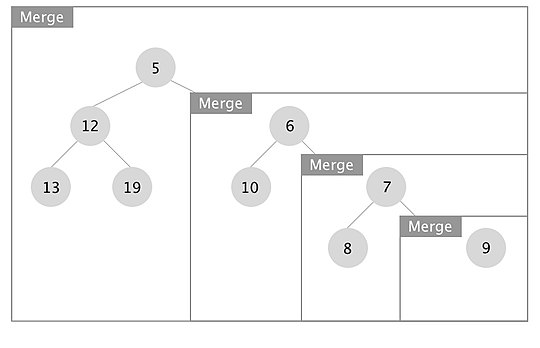
좌파 나무의 병합 작전이 어떻게 이루어지는지를 보여주는 예가 묘사되어 있다.상자는 각 병합 호출을 나타낸다.

재귀가 풀릴 때 x.right이면 좌, 우 아이들을 교환한다.s_value > x.left.s_value 모든 노드 x에 대한 값.이 경우 노드에서 루트된 하위 트리를 키 7과 10으로 교환했다.

최소 HBLT에 삽입

병합 작업을 사용하여 삽입한다.기존 노드에 노드 삽입

최소 HBLT는 크기가 1인 HBLT 트리를 해당 노드와 함께 생성하고 이를 기존 트리와 병합한다.

삽입 (A, x) B := CREATE_TREE(x) 반환 MERGE(A, B)

Min HBLT에서 Min 요소 삭제

Min HBLT의 Min 요소는 루트다.따라서 Min을 삭제하기 위해 루트를 삭제하고 그 하위 트리를 병합하여 새로운 Min HBLT를 형성한다.

DELETE_MIN(A) x := A.key A := MERGE (A.오른쪽, A.왼쪽) 리턴 x

높이 편향 좌익 트리 초기화

최소 HBLT 초기화 - 1부

키에 치우친 좌익 나무를 초기화하는 것은 주로 두 가지 방법 중 하나로 이루어진다.첫 번째는 각 노드를 한 번에 하나씩 HBLT로 병합하는 것이다.이 과정은 비효율적이고 시간이 걸린다.또 다른 방법은 각 노드와 결과 트리를 저장하는 데 큐를 사용하는 것이다.대기열의 처음 두 항목은 제거, 병합 및 다시 대기열에 배치된다.이것은 O(n) 시간에 HBLT를 초기화할 수 있다.이 접근방식은 제공된 3개의 도표에 자세히 설명되어 있다.작은 키에 치우친 좌익수 나무가 보인다.

최소 HBLT를 초기화하려면 트리에 추가할 각 요소를 대기열에 넣으십시오.예(왼쪽 1부 참조)에서 숫자 집합 [4, 8, 10, 9, 1, 3, 5, 6, 11]이 초기화된다.다이어그램의 각 선은 알고리즘의 또 다른 주기를 나타내며, 큐의 내용을 묘사한다.처음 다섯 단계는 따라 하기 쉽다.새로 만든 HBLT가 큐 끝에 추가된다는 점에 유의하십시오.다섯 번째 단계에서 1보다 큰 s-값이 처음 발생한다.여섯 번째 단계는 두 개의 나무가 서로 합쳐지는 것을 보여주며, 예측 가능한 결과를 보여준다.

최소 HBLT 초기화 - 2부

2부에서는 조금 더 복잡한 합병이 일어난다.값이 낮은 나무(나무 x)는 올바른 자식을 가지므로 나무 x의 오른쪽 아이와 다른 나무에 의해 뿌리내린 하위 트리에서 다시 합병을 호출해야 한다.하위 트리와 병합한 후 결과 트리는 다시 트리 x에 넣는다.오른쪽 아이의 s-값(s=2)이 이제 왼쪽 아이의 s-값(s=1)보다 크므로 반드시 교환해야 한다.루트 노드 4의 s-값도 현재 2이다.

최소 HBLT 초기화 - 3부

3부는 가장 복잡하다.여기서는 두 번 반복적으로 병합을 호출한다(각각 회색으로 비활성화되지 않은 오른쪽 아이의 하위 트리로).이것은 파트 2에 대해 설명한 것과 동일한 프로세스를 사용한다.

최소 HBLT에서 임의 요소 삭제

Min HBLT에 노드 x에 대한 포인터가 있으면 다음과 같이 삭제할 수 있다.노드 x를 두 하위 트리를 병합한 결과로 교체하고 x에서 루트로 경로에 있는 노드의 s 값을 업데이트하여 왼쪽 트리 속성을 유지하기 위해 필요한 경우 오른쪽 및 왼쪽 하위 트리를 스와핑하십시오.

우리가 뿌리를 내리거나 s-값이 변하지 않을 때까지 상승 횡단은 계속된다.요소를 삭제하기 때문에 통과된 경로의 S-값은 늘릴 수 없다.이미 부모의 올바른 자식이고 부모의 s-값이 감소하게 하는 모든 노드는 오른쪽에 남게 된다.부모의 왼쪽 자식이고 부모의 s-값이 감소하게 하는 모든 노드는 s-값이 오른쪽 자녀의 현재 s-값보다 낮아지면 오른쪽 형제와 교환해야 한다.

각 노드에는 상위 노드에 대한 포인터가 있어야 s-값을 업데이트하는 루트의 경로를 통과할 수 있다.

어떤 노드 y에서 트래버설이 끝나면, 노드는 모두 노드 y에 뿌리를 둔 가장 오른쪽 경로에 놓여 있다.예는 아래와 같다.따라서 통과된 노드 수는 최대 log(m)이며 m은 y에 뿌리를 둔 하위 트리의 크기가 된다.따라서 이 수술은 O(lg m)도 수행해야 한다.

무게 편향 좌익수^[5]

좌익수 역시 무게 편중될 수 있다.이 경우 s-값을 노드 x에 저장하는 대신, w(x)에 루트인 하위 트리에 노드 수를 나타내는 속성을 저장한다.x:

w(x) = w(x.오른쪽) + w(x.왼쪽) + 1

WBLT는 모든 내부 노드 x에 대해 w(x.왼쪽) w w(x.오른쪽)를 보장한다. WBLT 작업에서와 마찬가지로 오른쪽 하위 트리가 왼쪽 노드보다 클 때 노드의 하위 트리를 스와핑하여 이 불변성을 보장한다.

두 개의 최소 WBLT 병합

WBLT의 병합 작업은 하위 트리의 노드 수를 병합 재귀 호출 전에 알 수 있기 때문에 단일 상하 횡단보도를 사용하여 수행할 수 있다.따라서 오른쪽 하위 트리의 총 노드 수와 병합할 트리 수가 왼쪽 하위 트리의 노드 수보다 클 경우 왼쪽 하위 트리와 오른쪽 하위 트리를 교환할 수 있다.이를 통해 단일 경로로 작업을 완료할 수 있으므로 일정 인자에 의한 운영의 시간 복잡성을 개선할 수 있다.

병합 작업은 아래 그래프에 설명되어 있다.

WBLT의 기타 작업

최소 요소의 삽입 및 삭제는 병합 작업을 사용하는 HBLT와 동일하게 수행될 수 있다.

MIN 키의 병합, 삽입 및 삭제에서 WBLT가 HBLT를 상수 인수로 능가하지만, WBLT에서 임의 요소를 삭제할 때 O(log n) 바운드는 not(n) 노드를 통과해야 하기 때문에 보장되지 않는다.

만약 이것이 HBLT였다면, 키 60으로 리프 노드를 삭제하는 것은 O(1) 시간이 걸릴 것이고, 모든 노드에 대한 가장 오른쪽 경로의 길이는 변하지 않기 때문에 s-값을 업데이트할 필요가 없다.

그러나 WBLT 트리에서 우리는 각 노드의 무게를 다시 루트로 업데이트해야 하는데, 이것은 O(n) 최악의 경우를 가져온다.

변형

기본 좌익수에는 몇 가지 변형이 존재하며, 이는 기본 알고리즘을 약간 변경할 뿐이다.

• 키 큰 아이에 대한 왼쪽 아이의 선택은 자의적이다; "우파주의 나무"도 역시 효과가 있을 것이다.
• 아이를 교환하지 않고 대신 키가 가장 큰 아이(예: s-값 중 가장 유의하지 않은 비트)를 기록하고 병합 작업에서 이를 사용할 수 있다.
• 병합할 측면을 결정하는 데 사용되는 s-값은 높이 이외의 메트릭을 사용할 수 있다.예를 들어 무게(노드 수)를 사용할 수 있다.

참조

추가 읽기

• Robert E. Tarjan (1983). Data Structures and Network Algorithms. SIAM. pp. 38–42. ISBN 978-0-89871-187-5.
• Dinesh P. Mehta; Sartaj Sahni (28 October 2004). "Chapter 5: Leftist trees". Handbook of Data Structures and Applications. CRC Press. ISBN 978-1-4200-3517-9.

외부 링크

• 좌익수, 사르타즈 사니