이진 힙

이진(최소) 힙
유형	바이너리 트리 / 바이너리
발명된	1964
발명자	J. W. J. 윌리엄스
빅 O 표기의 시간 복잡도
알고리즘. 평균 최악의 경우 공간 O(n) O(n) 서치 O(n) O(n) 삽입 O(1) O(log n) 검색 최소값 O(1) O(1) 삭제 최소값 O(log n) O(log n)

이진 힙은 이진 트리 형식을 취하는 힙 데이터 구조입니다.바이너리 힙은 priority ^{[1]: 162–163} 큐를 구현하는 일반적인 방법입니다.이진 힙은 힙소트의 ^[2]데이터 구조로서 1964년에 J. W. J. 윌리엄스에 의해 도입되었습니다.

이진 힙은 다음 두 가지 추가 제약 조건이 ^[3]있는 이진 트리로 정의됩니다.

• 쉐이프 속성: 바이너리 힙은 완전한 바이너리 트리입니다.즉, 트리의 마지막 레벨(가장 깊은 레벨)을 제외한 모든 레벨이 가득 차 있습니다.트리의 마지막 레벨이 완전하지 않으면 해당 레벨의 노드가 왼쪽에서 오른쪽으로 채워집니다.
• 히프 속성: 각 노드에 저장되어 있는 키는 일부 전체 순서에 따라 노드 자녀 키보다 크거나 같거나 작습니다.

부모 키가 자녀 키보다 크거나 같은 힙을 max-heaps라고 하며, 부모 키가 자녀 키보다 작거나 같은 힙을 min-heaps라고 합니다.효율적인(로그 타임) 알고리즘은 바이너리 힙에 priority 큐를 실장하기 위해 필요한2가지 조작에 대해 알려져 있습니다.각각 요소를 삽입하고 최소 또는 최대 요소를 최소 또는 최대 힙에서 제거합니다.또한 이진 힙은 힙소트 정렬 알고리즘에 일반적으로 사용됩니다. 왜냐하면 이진 힙은 암묵적인 데이터 구조로서 구현될 수 있기 때문에 자식-부모 관계를 나타내기 위해 배열에 키를 저장하고 배열 내의 상대 위치를 사용할 수 있기 때문입니다.

히프 조작

삽입 및 제거 작업 모두 힙의 끝에 추가하거나 제거하여 먼저 모양 속성에 맞게 힙을 수정합니다.그런 다음 힙 위로 또는 아래로 이동하여 힙 속성을 복원합니다.두 작업 모두 O(log n) 시간이 걸립니다.

삽입

요소를 힙에 추가하려면 다음 알고리즘을 수행합니다.

1. 요소를 맨 왼쪽 빈 공간에 있는 힙의 맨 아래 레벨에 추가합니다.
2. 추가된 요소와 상위 요소를 비교합니다. 순서가 올바른 경우 중지하십시오.
3. 그렇지 않은 경우 요소를 부모 요소와 스왑하고 이전 단계로 돌아갑니다.

노드를 부모 노드와 비교 및 스왑하여 힙 속성을 복원하는 스텝2 및 3은 업히프 조작(버블업, 퍼콜레이트업, 시프트업, 트리클업, 수영, 힙파이업 또는 캐스케이드업이라고도 불립니다)이라고 불립니다.

필요한 작업 수는 힙 속성을 충족하기 위해 새 요소가 상승해야 하는 수준 수에 따라 달라집니다.따라서 삽입 조작은 최악의 경우 O(log n)의 시간 복잡도를 가집니다.랜덤 힙 및 반복 삽입의 경우 삽입 동작의 평균 대소문자 복잡도는 O(1)입니다.^[4][5]

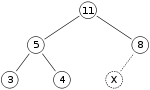
바이너리 힙 삽입의 예로서 max-heap이 있다고 합시다.

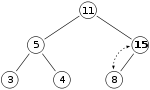
힙에 숫자 15를 추가하고 싶습니다.먼저 X 표시가 있는 위치에 15를 배치합니다.단, 15 >8부터 힙속성을 위반하고 있기 때문에 15와 8을 교환해야 합니다.첫 번째 스왑 후 힙은 다음과 같습니다.

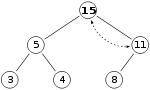
단, 15 > 11 이후 히프속성은 아직 위반되어 있기 때문에 다시 스왑해야 합니다.

유효한 최대값입니다.There is no need to check the left child after this final step: at the start, the max-heap was valid, meaning the root was already greater than its left child, so replacing the root with an even greater value will maintain the property that each node is greater than its children (11 > 5; if 15 > 11, and 11 > 5, then 15 > 5, because of t그는 transitive 관계).

압축풀기

히프 속성을 유지한 채 루트를 힙에서 삭제하는 절차는 다음과 같습니다(max-heap의 최대 요소 또는 min-heap의 최소 요소를 효과적으로 추출합니다).

1. 힙의 루트를 마지막 레벨의 마지막 요소로 바꿉니다.
2. 새 루트와 하위 루트를 비교합니다. 순서가 올바르면 중지합니다.
3. 그렇지 않은 경우 요소를 하위 항목 중 하나와 스왑하고 이전 단계로 돌아갑니다(작은 항목과 최대 항목에서 하위 항목과 스왑).

노드를 하위 노드 중 하나와 비교 및 스왑하여 힙 속성을 복원하는 스텝2와 3은 다운히프(버블다운, 퍼콜레이트다운, 시프다운, 싱크다운, 트리클다운, 힙파이다운, 캐스케이드다운, extract-min, extract-max 또는 단순히 힙파이프라고도 불립니다) 연산이라고 불립니다.

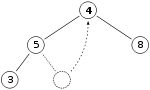
그럼, 만약 우리가 전과 같은 최대 히프를 가지고 있다면

11을 제거하고 4로 교체합니다.

8이 4보다 크기 때문에 힙 속성을 위반했습니다.이 경우 4와 8의 두 요소를 스왑하면 힙 속성을 복원할 수 있으므로 요소를 더 이상 스왑할 필요가 없습니다.

하향 이동 노드는 새 위치의 힙 속성을 충족할 때까지 최대 힙(min-heap에서는 더 작은 자식과 스왑됨)에서 더 큰 자식 노드와 스왑됩니다.이 기능은 길이(A)의 어레이 백업히프 A의 의사 코드로 정의된 Max-Heapify 함수에 의해 실현됩니다.A는 1부터 색인화 됩니다.

                 // max-heapify(A, i): 1부터 시작하는 히프를 나타내는 배열 // i: Max-Heapify(A, i): 왼쪽 ← 2×i + 1 가장 큰 ← if left left length(A) 및 왼쪽 > 왼쪽 > 왼쪽 >
                    if right a length(A) 및 A[right] > A[mough] 그렇다면: 가장 큰 ← 오른쪽 가장 큰 it hen hen hen swapA[i] 및 A[mough] Max-Heapifify(A, 최대)

위의 알고리즘이 어레이를 올바르게 재히핑하기 위해서는 인덱스 i의 노드 및 그 2개의 직계 하위 노드 이외의 노드가 힙 속성을 위반할 수 없습니다.요소가 삭제되지 않은 경우에도 (앞의 스왑을 사용하지 않고) 다운히프 조작을 사용하여 루트의 값을 변경할 수 있습니다.

최악의 경우, 새로운 뿌리까지, delete작업을 시간 복잡도는 나무의 키, 또는 O(로그 n)에 비례되어 그 체제의 바닥 수준에 도달하면 그 아이와 함께 각 층마다 바뀌어야 한다.

삽입 후 추출

요소는 더미에서 추출해 입력하 더 효율적으로 간단히 둘 다 upheap과downheap 작업을 수반하는 것은 삽입과 추출물 기능 위에 정의한, 전화를 할 수 있다.다음과 같이 대신에, 우리는,:몇 downheap 작업을 할 수 있다.

1. 우리가 추진하고 있는 품목을 제작하거나 체제의peeked 꼭대기가 더 큰(최대 더미로)을 비교해 보자.
2. 만약 그 체제의 뿌리:더 크다.
   1. 새로운 아이템이 가진 뿌리를 교체한다.
   2. Down-heapify의 뿌리를 뽑아 시작된다.
3. 그렇지 않을 경우, 우리가 추진하고 있는 물품을 반품하다.

파이선 삽입을 위한 기능 그 추출 그 아래 paraphrased은"heappushpop",를 제공합니다.[6][7]그 더미 배열 인덱스 1에 그것의 1번째 요소가 있는 것으로 추정된다.

//(맥스)힙엔 다음 표시되는 체제의 뿌리 추출한 신제품을 누른다. 끓여더미:배열 그 체제를 대표하는 1을 끓여항목:요소를 끓여 넣는 것에서 인덱스 처리는 그 두 사이에 품목과 체제의 뿌리의 더 큰를 반환합니다.Push-Pop(더미:List<.T>, 항목:T=->&T:힙 및 heap[1]을 빈 것은 아니다;항목://<>;만약분 힙 스왑 heap[1]과 item _downheap(더미 지수 1일부터 시작하는)수익 품목이다.

비슷한 기능과 그때를 삽입하는 Python으로"heapreplace"라고 불린다 먹기:정의될 수 있다.

//, 그리고 새로운 항목//더미를 밀다:배열 그 체제를 대표하는 1을 끓여항목:요소에서 인덱스 처리를 끓여삽입할 더미를 바꾸기(더미:List&lt의 현재 루트 반환합니다. 그 체제의 근을 구하다.T>, 항목:T=->. T:스왑 heap[1]과 _downheap(더미 지수 1일부터 시작하는)수익 항목 item.

서치

임의의 요소를 찾으려면 O(n) 시간이 걸립니다.

삭제

다음과 같이 임의의 요소를 삭제할 수 있습니다.

1. 삭제할 요소의 $i$를 찾습니다$.$
2. 이 요소를 마지막 요소와 스왑합니다.
3. 힙 속성을 복원하려면 다운히파이 또는 업히파이.max-heap(min-heap)에서는 상위 요소의 힙 속성만 위반될 수 있으므로 요소$i$의$$새 키가 이전 키보다 큰(작은) 경우에만 $up-heapify$가 필요합니다.요소가 스왑되기 $전$에 요소$i$와 $요소$i의 자식 간에 힙 속성이 유효하다고 가정하면 현재 더 큰(작은) 키 값으로 위반될 수 없습니다.새로운 키가 이전 키보다 작을 경우(크게 할 경우)에는 하위 요소에서만 힙 속성을 위반할 수 있으므로 다운히파이만 필요합니다.

감소 또는 증가 키

감소 키 조작은 지정된 값을 가진 노드의 값을 낮은 값으로 대체하고 증가 키 조작은 동일한 값을 더 높은 값으로 대체합니다.여기에는 지정된 값을 가진 노드를 찾아 값을 변경한 다음 힙 속성을 복원하기 위해 다운히핑 또는 업히핑이 포함됩니다.

감소 키는 다음과 같이 수행할 수 있습니다.

1. 수정할 요소의 인덱스를 찾습니다.
2. 노드 값 감소
3. 힙 속성을 복원하기 위한 다운히파이(최대 힙으로 가정)

증가 키는 다음과 같이 수행할 수 있습니다.

1. 수정할 요소의 인덱스를 찾습니다.
2. 노드 값 증가
3. 힙 속성을 복원하기 위한 업히파이(최대 힙으로 가정)

히프를 쌓다

n개의 입력 요소 배열에서 힙을 구축하는 방법은 빈 힙에서 시작하여 각 요소를 순차적으로 삽입하는 것입니다.바이너리 힙의 발명자의 이름을 따서 Williams의 방법이라고 불리는 이 접근법은 O(n log n) 시간에 실행되는 것으로 쉽게 볼 수 있습니다. ^[a]각 O(log n) 비용으로 n개의 삽입을 수행합니다.

그러나 윌리엄스의 방식은 차선책이다.Floyd에 의한^[8] 보다 빠른 메서드는 쉐이프 속성을 고려하여 요소를 바이너리 트리에 임의로 배치하는 것으로 시작합니다(트리는 배열로 나타낼 수 있습니다).그런 다음 가장 낮은 수준에서 시작하여 위로 이동하면 삭제 알고리즘에서처럼 각 하위 트리의 루트를 아래로 체로 쳐서 힙 속성이 복원됩니다.좀 더 구체적으로 말하면, 어떤$높이$에서 시작하는$$ $모든$ 하위 트리가 이미 "증명"(h$= 0$에 $해당$하는 최하위 수준)$$된 경우, $높이{\displaystyle }$h + $(\displaystyle$ h$+1)$의 트리는 건물을 지을 때 최대 가치 어린이 경로를 따라 뿌리를 내려감으로써 수북이 쌓일 수 있습니다.max-min-min-min-min-min-min-min-min-min-min이 프로세스에는 노드당 O$)\style$ O($h)\display$ O(h)}의$$ 조작(스왑)이 $필요$합니다.이 방법에서는 힙화의 대부분은 하위 수준에서 수행됩니다.히프의 높이는${\displaystyle \log }$ n${\$ { \ $displaystyle$ \$lfloor$ \ $rfloor$이므로$높이h$의 노드 수는${\displaystyle }$2 ${\displaystyle \frac{{\log }^{}}{}}$log${\displaystyle \frac{{}^{}}{{\mathrm{}}^{}}}$2 ${\displaystyle \frac{h^{}}{}\frac{{\mathrm{}}^{}}{}}$ ${\displaystyle \frac{2^{}}{}}$ h$$nn { $displaystyle$\$frac${ $2$^ { \ $lfloor$ \ $loor$} { h$$} { h } } $。$따라서 모든 서브트리를 히프화하는 비용은 다음과 같습니다.

$({displaystyle {argined}\sum _{h=0}^{\lfloor \lfloor \lfloor _{h=0})O(h)&=O\left(n\sum _{h=0}^{\lfloor \loor }{\frac {2^{h}\}\lfloor =\loor }\loor}\fright)$

이는 주어진 무한 급수$\underset{\mathrm{i}}{\overset{}{}}$ i $\underset{}{\overset{}{=}}$ 0$\underset{}{\overset{}{}}i{\mathrm{}}^{}$ / $2^{}$i { $textstyle \sum$ _ ${i=0}^{\infty }i/2^{i}}$가 수렴한다는 사실을 이용한다.

위의 정확한 값(히프 구축 중 최악의 경우 비교 횟수)은 다음과 같습니다.

${\displaystyle 2}$n - ${\displaystyle {}_{}}$ ${\displaystyle {s\mathrm{}}_{}}$2 (${\displaystyle n}$) - ${\displaystyle {e\mathrm{}}_{}}$2 (${\displaystyle n}$ $){$ $displaystyle 2n-2s_{2}(n)-e_{2}(n$^[9][b]

여기서₂ s(n)는 n의 2진수 표현의 모든 자릿수의 합이고₂ e(n)는 n의 소인수 분해에서 2의 지수이다.

평균 사례는 분석하기가 더 복잡하지만 1.8814 n - 2 logn₂ + O(1) 비교에 점근적으로 ^[10][11]접근하는 것으로 나타날 수 있습니다.

이어지는 빌드-맥스-히프 함수는 Max-Heapify(Max-Heap의 경우 다운-히프)를 반복적으로 사용함으로써 n개의 노드를 가진 완전한 바이너리 트리를 저장하는 어레이 A를 Max-Heap으로 변환합니다.floor(n/2) + 1, floor(n/2) + 2, ..., n에 의해 인덱스된 배열 요소는 모두 트리의 리프입니다(인덱스가 1에서 시작된다고 가정합니다).따라서 각 요소는 1개의 엘리먼트히프이므로 다운히프할 필요가 없습니다.Build-Max-Heap은 나머지 각 트리 노드에서 Max-Heapify를 실행합니다.

빌드-최대-히프(A): 바닥(길이(A)/2)에서 1도까지의 각 인덱스 i: Max-Heapify(A, i)

히프 실장

힙은 일반적으로 어레이와 함께 구현됩니다.모든 이진 트리를 배열에 저장할 수 있지만 이진 힙은 항상 완전한 이진 트리이기 때문에 콤팩트하게 저장할 수 있습니다.포인터에는 공백이 필요 없습니다.대신 각 노드의 부모 및 자녀는 배열 인덱스에서 산술적으로 찾을 수 있습니다.이러한 속성을 통해 이 힙 구현은 암묵적인 데이터 구조 또는 Anentafel 목록의 단순한 예가 됩니다.자세한 내용은 루트 위치에 따라 달라지며, 루트 위치는 구현에 사용되는 프로그래밍 언어의 제약 조건 또는 프로그래머 선호도에 따라 달라질 수 있습니다.구체적으로는 산술을 단순화하기 위해 루트를 인덱스1에 배치하는 경우가 있습니다.

n은 힙 내의 요소 수이고 i는 힙을 저장하는 어레이의 임의의 유효한 인덱스입니다.트리 루트가 인덱스 0에 있고 유효한 인덱스가 0 ~n - 1인 경우 각 요소 a at 인덱스 i는

• 지수 2i + 1 및 2i + 2의 하위 항목
• 인덱스 플로어((i - 1) / 2)의 부모.

또는 트리 루트가 인덱스 1에 있고 유효한 인덱스 1~n이 있는 경우 각 요소 a at 인덱스 i는

• 지수 2i 및 2i +1의 하위 항목
• 인덱스 플로어(i / 2)에 있는 부모.

이 실장은 입력 배열에 할당된 공간을 힙을 저장하기 위해 재사용하는 힙소트 알고리즘에서 사용됩니다(즉, 알고리즘이 인플레이스 처리됨).이 실장은 priority 큐로도 도움이 됩니다.동적 배열을 사용하면 무제한 수의 항목을 삽입할 수 있습니다.

그런 다음 upheap/downheap 연산은 다음과 같이 배열로 나타낼 수 있습니다. b, b+1, ..., e 인덱스에 대해 힙 속성이 유지된다고 가정합니다. sifter-down 함수는 힙 속성을 b-1, b, b+1, ..., e로 확장합니다. i = b-1만 힙 속성을 위반할 수 있습니다.j를 b, …의 범위 내(max-heap의 경우 또는 min-heap의 경우 가장 작은 아이)의 인덱스로 합니다(2i > e로 인해 이러한 인덱스가 존재하지 않는 경우 힙 속성은 새로 확장된 범위를 유지하므로 수행할 필요가 없습니다).값 a[i]와 a[j]를 교환함으로써 위치 i의 힙 속성을 확립한다.이 시점에서 유일한 문제는 히프속성이 인덱스j에 대해 유지되지 않을 수 있다는 것입니다.모든 요소에 대해 힙 속성이 확립될 때까지 시프다운 함수는 인덱스 j에 테일 리커버리 방식으로 적용됩니다.

체를 거르는 기능이 빠릅니다.각 단계에서 2개의 비교와 1개의 스왑만 필요합니다.동작하고 있는 인덱스 값은 반복할 때마다 2배가 되기 때문에 로그 스텝이 많이 필요합니다₂.

큰 힙이나 가상 메모리를 사용하는 경우, 위의 스킴에 따라 요소를 어레이에 저장하는 것은 비효율적입니다. (거의) 모든 레벨이 다른 페이지에 있습니다.B히프는 하위 트리를 한 페이지에 유지하는 이진 힙으로, 액세스되는 페이지 수를 최대 ^[12]10배까지 줄입니다.

두 개의 이진 힙을 병합하는 작업은 동일한 크기의 힙에 대해 δ(n)가 필요합니다.최선의 방법은 (어레이 구현의 경우) 2개의 히프 어레이를 연결하고 그 ^[13]결과 히프를 구축하는 것입니다.n개 요소의 힙은 O(log n log k) 키 비교를 사용하여 k개 요소의 힙과 병합할 수 있으며, 포인터 기반의 구현의 경우 O(log n log k) ^[14]시간 내에 병합할 수 있다.서브히프의 순서집합으로서의 힙의 새로운 뷰에 근거해, n요소상의 힙을 k요소상의 2개의 힙으로 분할하는 알고리즘이 ^[15]에 제시되었다.이 알고리즘에서는 O(log n * log n)의 비교가 필요합니다.또한 뷰는 힙을 병합하기 위한 개념적으로 단순한 새로운 알고리즘을 제공합니다.병합이 일반적인 작업인 경우 O(log n)에서 병합할 수 있는 이항 힙과 같은 다른 힙 구현을 권장합니다.

또, 바이너리 힙은 기존의 바이너리 트리 데이터 구조로 실장할 수 있지만, 요소를 추가할 때 바이너리 힙의 마지막 레벨에서 인접 요소를 찾는 문제가 있습니다.이 요소는 알고리즘적으로 결정하거나 트리에 "스레딩"이라고 불리는 추가 데이터를 노드에 추가하여 결정할 수 있습니다. 단순히 하위 항목에 대한 참조를 저장하는 것이 아니라 노드의 순서도 순서대로 저장합니다.

히프 구조를 변경하여 O$($${\displaystyle \log n}$n$)\$displaystyle(\log n$)$ 시간$$ ^[16]내에 $가능$한 최소 및 최대 요소를 추출할 수 있습니다.이를 위해 행은 min 힙과 max-heap을 번갈아 사용합니다.알고리즘은 거의 동일하지만 각 단계에서 번갈아 비교되는 행을 고려해야 합니다.퍼포먼스는 일반 단방향 힙과 거의 동일합니다.이 아이디어는 min-max-median 힙으로 일반화할 수 있습니다.

지수 방정식의 도출

어레이 기반 힙에서는 노드의 자식과 부모를 노드 인덱스의 간단한 산술로 찾을 수 있습니다.이 절에서는 근이 지수 0인 힙에 대한 관련 방정식을 도출하고, 근이 지수 1인 힙에 대한 추가 참고 사항을 도출한다.

혼란을 피하기 위해 노드의 레벨을 루트로부터의 거리로 정의하여 루트 자체가 레벨0을 차지하도록 하겠습니다

자노드

인덱스 i(0부터 시작)에 있는 일반 노드의 경우 오른쪽 $=$ ${\displaystyle 2}$i +$$2 (\$displaystyle$\text${right$}=$2i$+2$)$의$$${\displaystyle \text{인덱스}}$를 먼저 도출합니다$.$

노드 i를 레벨 L에 배치하고 레벨 L에는 $정확히{\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {2개}^{}}$의$$노드(\$displaystyle$ 2$^{l})$가 포함되어 있습니다.또한 l층과 l층을 포함하는 층에는 $정확히{\displaystyle {\mathrm{}}^{}}$ 2${\displaystyle l^{}}$ +${\displaystyle {}^{}{1}^{}}$ -$$ { $displaystyle$ 2$^{l+1$}-1$}개$의 노드가 포함되어 있습니다(이진 산술; 0111...displays = 1000...).000 - 1).루트는 0에 저장되기 때문에 k번째 노드는 ${\displaystyle \mathrm{인덱스}}($$k$-$$1$$)에 $저장$됩니다.이러한 관찰을 종합하면 레이어 L의 마지막 노드의 인덱스에 대해 다음과 같은 식을 얻을 수 있습니다.

${\displaystyle\text{last}(l)=(2^{l+1}-1)-1=2^{l+1}-2)$

레이어 L의 노드 i 뒤에 j개의 노드가 존재하도록 합니다.

$({displaystyle {alignedat}{2}i=&\squad {text{last}}(L)-j\=&\quad(2^{L+1}-2)-j\end{alignedat}}})$

각 j 노드에는 정확히 2개의 하위 노드가 있어야 합니다.따라서 레이어 끝에서 i의 오른쪽 하위 노드(${\displaystyle }$+$$ \$displaystyle$ $L$$+1)$를 분리하는 ${\displaystyle \mathrm{2개}}$의$$j노드가 있어야 $합니다{\displaystyle \mathrm{}}$.

${\displaystyle {\text{right}=&\text{last(L + 1)}}-2j\=&\display (2^{L+2}-2)-2j\=&\quad 2(2^{L+1}-2-j)+2\=&quad 2\ad+2} 정렬$

필요에 따라서.

$노드$의 왼쪽 자식은 항상 오른쪽 자식보다 한 자리 앞에 있으므로 왼쪽 $=$ 2 ${\displaystyle i}$ +$style${left$}}=$2 i + 1)이$됩니다$

루트가 0이 아닌 인덱스 1에 위치하는 경우 각 레벨의 마지막 노드는 ${\displaystyle {인덱스2}^{}}$ l${\displaystyle {}^{}}$+ 1 -$$({$display style$$2^{l+1$}-1$)$입니다. 이를 사용하면 루트가 1개 있는 경우 왼쪽 $=$${\displaystyle 2}$ i + 1$({$displaystyle {$left$}}=${\displaystyle \text{2i<img alt="text{left} = 2i" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/cbc36e0d7f83009322861ddecd75efee1bce3def" style="vertical-align: -0.338ex; width:8.359ex; height:2.176ex;">}}$$)$ 및 ${\displaystyle \mathrm{오른쪽}}$ $=$2 ${\displaystyle \mathrm{i}}$+ 1$({displaystyleft}=2i+$1)이 ${\displaystyle \text{됩니다}}$.

부모 노드

모든 노드는 부모의 왼쪽 또는 오른쪽 자식이므로 다음 중 하나에 해당함을 알 수 있습니다.

1. ${\displaystyle i=2\times({\text{parent}})+1}$
2. ${\displaystyle i=2\times({\text{parent}})+2}$

이런 이유로,

${\displaystyle {\text{parent}}=parentfrac {i-1}{2}\;{\textrm {or}\;{\frac {i-2}{2}}$

이제 표현 ${\displaystyle {\displaystyle \frac{\text{'}}{}}i{\displaystyle \frac{}{}}}$ - ${\displaystyle {\displaystyle \frac{\mathrm{}}{}}}$ 2$'$ ({$displaystyle \ left$ \ $lfloor$\$dfrac${ i - $1 }$ {2} ) \$right$ \ $rfloor$ $\}$ )에 대해 생각해 보겠습니다.

$노드{\displaystyle }$ i$(\displaystyle$ i$)$가 왼쪽 아이일 경우 즉시 결과가 나타나지만 $노드{\displaystyle }$ i$(\displaystyle$ i$)$가 오른쪽 아이일 경우 올바른 결과도 나타납니다.이 경우${\displaystyle }$(${\displaystyle i}$ ${\displaystyle -}$ ${\displaystyle 2}$)$${$displaystyle (i-2)}$은 짝수여야 하며$,{\displaystyle }$ 따라서 (${\displaystyle i}$-${\displaystyle 1}$)$${$displaystyle (i-1)}$은(는) 홀수여야 합니다.

$(\displaystyle {argentat} {2} \ lfloor = & \ dfrac { i - 1 } { 2 } + { \ dfrac { i - 2 } \ lfloor \ = \ dfrac { i - 2 } { \ text } )$

따라서 노드가 왼쪽 자식인지 오른쪽 자식인지에 관계없이 다음 식으로 부모를 찾을 수 있습니다.

$(\displaystyle\text{parent}=\lfloor {dfrac {i-1}{2}}\right\loor)$

관련 구조

힙 내의 형제자매의 순서는 힙 속성에 의해 지정되지 않기 때문에 단일 노드의 두 자녀는 쉐이프 속성을 위반하지 않는 한 자유롭게 교환할 수 있습니다(treap과 비교).다만, 공통 어레이 베이스의 힙에서는, 단순히 아이를 스왑 하는 것만으로, 아이의 서브 트리 노드를 이동해 힙 속성을 유지할 필요가 있는 경우가 있습니다.

이진 힙은 d= 2인 d-ary 힙의 특수한 경우입니다.

실행 시간 요약

다음은 다양한 힙 데이터 구조의 시간^[17] 복잡성입니다.함수명은 min-heap을 전제로 합니다."O(f)" 및 "δ(f)"의 의미는 빅 O 표기법을 참조하십시오.

작동	find-min	삭제 최소값	삽입하다	감소 키	혼재
바이너리[17]	θ(1)	δ(로그 n)	O(log n)	O(log n)	θ(n)
좌파	θ(1)	δ(로그 n)	δ(로그 n)	O(log n)	δ(로그 n)
이항[17][18]	θ(1)	δ(로그 n)	θ(1)[c]	δ(로그 n)	O(log n)[d]
피보나치[17][19]	θ(1)	O(log n)[c]	θ(1)	θ(1)[c]	θ(1)
페어링[20]	θ(1)	O(log n)[c]	θ(1)	o(로그 n)[c][e]	θ(1)
브로달[23][f]	θ(1)	O(log n)	θ(1)	θ(1)	θ(1)
랭크 페어링[25]	θ(1)	O(log n)[c]	θ(1)	θ(1)[c]	θ(1)
엄밀한 피보나치[26]	θ(1)	O(log n)	θ(1)	θ(1)	θ(1)
2 ~ 3 히프[27]	O(log n)	O(log n)[c]	O(log n)[c]	θ(1)	?

「 」를 참조해 주세요.

• 히프
• 힙소트

레퍼런스

외부 링크

• 개방형 데이터 구조 - 섹션 10.1 - 이진힙: 암묵적인 이진 트리, Pat Morin
• Robin Thomas에 의한 C의 바이너리 최대 힙 구현
• Robin Thomas에 의한 C의 바이너리 최소 힙 구현