인터벌 트리
Interval tree컴퓨터 과학에서 인터벌 트리는 간격을 유지하기 위한 트리 데이터 구조다.구체적으로는 주어진 간격이나 점과 겹치는 모든 간격을 효율적으로 찾을 수 있도록 한다.예를 들어,[1] 직사각형 뷰포트 내의 컴퓨터화된 지도에서 모든 도로를 찾거나, 3차원 장면 내에서 모든 가시적 요소를 찾기 위해 쿼리를 윈도우로 설정하는 데 종종 사용된다.유사한 데이터 구조가 세그먼트 트리 입니다.
사소한 해결책은 각 구간을 방문하여 주어진 점이나 구간을 교차하는지 시험하는 것인데, 에는 O( ) 시간이 필요하며, 서 n 은 집합의 구간 수입니다.쿼리는 모든 간격을 반환할 수 있으므로, 예를 들어 쿼리가 수집의 모든 간격을 교차하는 큰 간격인 경우 이는 점증적으로 최적이지만, 런타임이 쿼리에 의해 생성되는 간격의 m{\ 단위로 표현되는 출력 민감 알고리즘을 고려함으로써 더 나은 결과를 얻을 수 있다.y. Interval trees have a query time of and an initial creation time of , while limiting memory consumption to . After creation, interval trees may be dynamic, allowing efficient insertion and deletion of an interval in ) O n시간.만약 간격의 끝점 작은 정수 범위(예를 들어, 범위에서,[1,…, O(nx]{\displaystyle[1,\ldots ,O(nx]})내에, 더 빠르게 그리고 사실로 최적화 데이터 구조'연속 예비 처리'시간 O(n){O(n)\displaystyle}과 함께 exist[2][3]이 질문 응답 시간 O(1+m)m{\displa를 신고하면{O(1+m)\displaystyle}.ystyl 쿼리 지점을 포함하는 m 간격(매우 간단한 쿼리 점은 참조[2]).
순진한 접근법
간단한 경우 간격이 겹치지 않고 단순한 이진 검색 트리에 삽입하여 ) 시간 내에 쿼리할 수 있다.다만 임의로 겹치는 구간이 있는 경우 시작점별로 정렬된 순서나 끝점별로 정렬된 순서가 다를 수 있으므로 트리에 삽입하기 위한 두 구간을 비교할 방법이 없다.순진한 접근법은 두 개의 평행 트리를 만드는 것일 수도 있는데, 하나는 시작점에 의해, 그리고 하나는 각 간격의 끝점에 의해 주문된 것이다.이렇게 하면 각 트리의 절반을 ) n시간 내에 폐기할 수 있지만, 결과는 병합되어야 하므로 시간이 필요하다.이것은 에게 (+ n)= O( ) n의 질의를 주는데, 이것은 무차별적인 힘보다 나을 것이 없다
인터벌 트리가 이 문제를 해결한다.이 글에서는 중심 구간 트리와 증강 트리로 불리는 구간 트리의 두 가지 대체 설계를 설명한다.
중심 간격 트리
쿼리는 O + ) 시간이 필요하며, 은(는) 총 간격 수입니다. 은 보고된 결과 수입니다.시공에는 ) n시간이 필요하고, 저장에는 공간이 필요하다.
건설
숫자 라인에 개의 구간이 설정된 경우, 다른 구간이나 점이 겹치는 모든 구간을 효율적으로 검색할 수 있도록 데이터 구조를 구성하고자 한다.
우리는 모든 구간의 전체 범위를 취하여 x 에서 반으로 나누는 것으로 시작한다(실제적으로 x 이렇게 하면 세 가지 세 가지 구간이 주어지는데, 이 은 x 의 왼쪽에 완전히 있고 이 구간은 x 의 오른쪽에 완전히 있는 구간이며, 이 구간은 s }이라고 한다.및 겹치는 x 과(와) 함께 S 라고 부르겠다
S 과(와) 의 간격은 남은 간격이 없을 때까지 같은 방식으로 재귀적으로 나뉜다.
중앙점과 겹치는 의 구간은 구간 트리의 노드에 연결된 별도의 데이터 구조에 저장된다.이 데이터 구조는 시작점에 따라 정렬된 모든 구간을 포함하는 목록과 끝점에 따라 정렬된 모든 구간을 포함하는 목록 두 개로 구성된다.
그 결과 각 노드가 저장되는 이진 트리가 생성:
- 중심점
- 중앙점 왼쪽의 모든 구간을 포함하는 다른 노드에 대한 포인터
- 중앙점 오른쪽에 있는 모든 구간을 포함하는 다른 노드에 대한 포인터
- 시작점별로 정렬된 중앙점과 겹치는 모든 구간
- 끝점별로 정렬된 중앙점과 겹치는 모든 구간
교차
위에서 구축된 데이터 구조를 감안하여 범위나 포인트로 구성된 쿼리를 받고, 이 입력과 겹치는 원래 세트의 모든 범위를 반환한다.
포인트로
이 작업은 지정된 점 과(와) 겹치는 트리의 모든 간격을 찾는 것이다트리는 전통적인 2진수 트리를 횡단하는 데 사용되는 것과 유사한 재귀 알고리즘을 사용하여 걷지만, 각 노드의 "중앙" 지점과 겹치는 간격 검색을 지원하는 추가적인 논리로 걷는다.
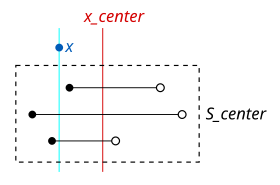
각 트리 노드에 대해 을(를) 위의 노드 구성에 사용되는 중간점인x {과(와) 비교한다. 이가) x 보다 작은 경우, S 이(가) 고려된다. 이가) x 보다 크면 S 이가) 고려된다.
루트부터 리프까지 트리를 가로지르면서 각 노드가 처리됨에 따라 S 의 범위가 처리된다. 이(가) x 보다 작으면 우리는 S {\의 모든 이 x 중심 이후에 끝나거나 또는 x {\}과 겹칠 수 것을 알고 있다 따라서 o. 이전에 시작하는 S 에서 이러한 간격을 찾을 수 있으며 이미 구성된 S 의 목록을 참조할 수 있다.우리는 이 시나리오의 시작 간격에만 신경을 쓰기 때문에 시작별로 정렬된 리스트를 참조할 수 있다.이 목록에서 보다 작은 가장 가까운 숫자를 찾았다고 가정합시다.목록의 처음에서 발견된 지점까지의 모든 범위는 보다 큰 x x}보다 먼저 시작하고 이(가) 이후에 끝나기 에 {\ 과 겹친다.따라서 시작점 값이 을(를) 초과할 때까지 간단히 목록의 간격을 열거할 수 있다
마찬가지로 이가) x 중심 x_{\ {보다크면 S 의 모든 이 x{\보다 먼저 시작되어야 한다는 것을 알 수 있으므로, 정렬된 b 목록을 하여 x diskn 후에 끝나는 구간을 찾을 수 있다.y 간격 끝.
이(가) x 과(와) 정확히 일치하는 경우, 추가 없이S 센터 {\S_{\{center}의 모든 간격을 결과에 추가할 수 있으며 트리 통과를 중지할 수 있다
간격을 두고
결과 간격 이(가) 쿼리 간격 과(와) 교차하려면 다음 중 하나가 유지되어야 한다.
- 의 시작점 및/또는 끝점이 ; 또는
- 은 q {\displaystyle q을(를 완전히 감싸고
이 글은 독자들에게 혼란스럽거나 불명확할 수 있다.(2020년 2월)(이를 과 시기 |
먼저 별도로 된트리를 사용하여 q {\displaystyle 내에서 시작점 및/또는 끝점이 있는 모든 간격을 찾는다.1차원 사례에서, 우리는 각각 해당하는 간격으로 포인터를 가지고 설정된 간격의 모든 시작점과 끝점을 포함하는 검색 트리를 사용할 수 있다. 의 시작과 끝에 대해 로그) O n시간 내에 이진 검색하면 고려해야 할 최소 및 최대 포인트가 나타난다.이 범위 내의 각 점은 과(와) 겹치고 결과 목록에 추가된 간격을 참조한다.간격은 내에서 시작하고 끝날 수 있으므로 중복이 발생하지 않도록 주의해야 한다 이는 각 간격마다 이진 플래그를 사용하여 결과 집합에 추가되었는지 여부를 표시할 수 있다.
마지막으로 을(를) 둘러싸는 간격을 찾아야 한다 이를 찾기 위해 내부의 어떤 점을 선택하고 위의 알고리즘을 사용하여 해당 점을 교차하는 모든 간격을 찾는다(again, 중복 제거를 주의).
상위 치수
구간 트리 데이터 구조는 조회 및 시공 시간이 동일한 상위 N 과) {\ n 공간으로 일반화할 수 있다.
먼저, 차원의 범위 트리는 쿼리 R 내부의 시작점과 끝점에 있는 모든 구간을 효율적으로 검색할 수 있도록 구성된다 일단 해당 범위가 발견되면, 남은 것은 일부 차원으로 영역을 둘러싸는 범위뿐이다.이러한 중첩을 찾기 위해 N 간격 트리가 생성되고 R을 교차하는 하나의 축이 각각 쿼리된다.예를 들어, 2차원에서는 R R R R과 교차하는 다른 수평선의 하단을 수평축에 대해 구성된 구간 트리에 대해 쿼리한다.마찬가지로 왼쪽( R R을를) 교차하는 다른 수직선도 수직 축에 구성된 구간 트리에 대해 쿼리할 수 있다.
각 구간 트리는 더 높은 치수를 위해 추가가 필요하다.트리에서 이동하는 각 노드에서 을(를) S 과(와) 비교하여 중복된 부분을 찾는다.1차원 사례에서 사용된 것과 같이 두 개의 점의 정렬된 리스트 대신 범위 트리가 구성된다.이를 통해 영역 과(와) 겹치는 S 의 모든 포인트를 효율적으로 검색할 수 있다
삭제
트리에서 간격을 삭제한 후, 해당 간격을 포함하는 노드에 더 이상의 간격이 없는 경우, 해당 노드는 트리에서 삭제될 수 있다.이것은 일반적인 바이너리 트리 삭제 작업보다 더 복잡하다.
간격은 트리에 있는 여러 노드의 중심점과 겹칠 수 있다.각 노드는 모든 구간을 왼쪽 하위 트리에 완전히 왼쪽의 중앙점 구간으로 저장하기 때문에, 마찬가지로 오른쪽 하위 트리에서도 각 구간이 중복되는 노드 집합에서 루트에 가장 가까운 노드에 저장된다.
바이너리 트리의 정상적인 삭제 작업(삭제되는 노드의 경우 두 개의 하위 트리의 경우)은 삭제되는 노드의 위치(대개 오른쪽 하위 트리의 가장 왼쪽 하위 트리 또는 왼쪽 하위 트리의 가장 오른쪽 하위 트리)로 노드를 승격하는 것을 포함한다.
이 프로모션의 결과, 승격 노드 위에 있던 일부 노드가 그 하위 노드가 된다. 승격 노드에도 겹치는 간격을 검색하여 승격 노드로 이 간격을 이동시킬 필요가 있다.결과적으로, 이 경우 삭제해야 하는 새로운 빈 노드가 동일한 알고리즘을 다시 따를 수 있다.
밸런싱
삭제에 영향을 미치는 동일한 문제는 회전 작업에도 영향을 미친다. 회전은 노드가 가능한 한 루트에 가깝게 저장되는 불변성을 보존해야 한다.
증강나무

간격을 나타내는 또 다른 방법은 코멘 외 에 설명되어 있다. (2009, 섹션 14.3: Interval tree, 페이지 348–354).
삽입과 삭제 모두 ) 시간이 필요하며, 은 삽입 또는 삭제 작업 전 트리의 총 간격 수입니다.
증강 트리는 단순 순서 트리(예: 바이너리 검색 트리 또는 자가 균형 바이너리 검색 트리)에서 만들 수 있으며, 간격의 '낮은' 값으로 정렬된다.그런 다음 모든 노드에 주석을 추가로 추가하여 이 노드의 하향된 모든 간격 중 최대 상한 값을 기록한다.이 속성을 유지하려면 노드를 추가하거나 삭제할 때마다 노드의 모든 상위 항목을 아래에서 위로 업데이트해야 한다.이 작업은 노드 추가 또는 제거당 O(h) 단계만 수행되며, 여기서 h는 트리에서 추가 또는 제거된 노드의 높이입니다.삽입 및 삭제 중에 트리가 회전하는 경우 영향을 받는 노드도 업데이트해야 할 수 있다.
Now, it is known that two intervals and overlap only when both and . When searching the trees for nodes overlap지정된 간격으로 ping을 수행하면 즉시 건너뛸 수 있음:
- 낮은 값이 지정된 간격의 끝을 초과한 노드의 오른쪽에 있는 모든 노드.
- 지정된 간격의 시작보다 낮은 최대 고값을 갖는 모든 노드
구성원 자격 쿼리
트리가 불필요한 횡단을 피하면 어느 정도 성과를 얻을 수 있다.이는 이미 존재하는 간격을 추가하거나 존재하지 않는 간격을 제거할 때 발생할 수 있다.
총 순서는 간격에 대해 하한으로 먼저 정렬하고 상한으로 정렬하여 정의할 수 있다. 다음 K 간격이 삽입 또는 제거될 간격과 겹칠 경우 중복 항목을 찾는 데 필요한 + )와 비교하여 O + log 시간대 O로 멤버십 검사를 수행할 수 있다.이 솔루션은 추가 구조가 필요하지 않다는 장점이 있다.그 변화는 완전히 알고리즘적이다.단점은 멤버십 쿼리가 ) O n시간이 걸린다는 점이다.
또는 () 메모리의 비율로 예상 상수 시간에 있는 멤버쉽 쿼리를 해시 테이블로 구현하여 간격 트리와 함께 lockstep으로 업데이트할 수 있다.간격이 값이 아닌 참조에 의해 저장되는 경우, 이것은 반드시 총 메모리 요구량의 두 배가 아닐 수 있다.
Java 예제:트리에 새 간격 추가
각 노드의 키는 구간 자체로서, 노드는 낮은 값으로 먼저 정렬되고 마지막으로 높은 값으로 정렬되며, 각 노드의 값은 구간의 끝점이다.
공중의 공허하게 하다 덧셈을(간격 i) { 놓다(i, i.getEnd()); } Java 예제: 트리에서 점 또는 간격 검색
간격을 검색하려면 키를 사용하여 트리를 걷는다.n.getKey()) 및 높은 값(n.getValue()쿼리를 겹칠 수 없는 분기를 생략한다.가장 간단한 경우는 포인트 쿼리:
// "p"를 포함하는 모든 간격 검색(부터) // 노드 "n" 및 일치 구간을 목록 "interval"에 추가 공중의 공허하게 하다 샅샅이 뒤지다(IntervalNode n, 포인트 p, 리스트<간격> 결과) { // 존재하지 않는 노드 검색 안 함 만일 (n == 무효의) 돌아오다; // p가 임의 구간의 가장 오른쪽 점의 오른쪽에 있는 경우 // 이 노드와 모든 어린이의 경우 일치하는 항목이 없을 것이다. 만일 (p.비교(n.getValue()) > 0) 돌아오다; // 왼쪽 자녀 검색 샅샅이 뒤지다(n.get Left(), p, 결과); // 이 노드 확인 만일 (n.getKey().포함하다(p)) 결과.덧셈을(n.getKey()); // p가 이 간격 시작의 왼쪽에 있는 경우, // 그러면 오른쪽의 어떤 아이에게도 있을 수 없다. 만일 (p.비교(n.getKey().getStart()) < 0) 돌아오다; // 그렇지 않으면 오른쪽 아이를 검색하십시오. 샅샅이 뒤지다(n.겟라이트(), p, 결과); } 어디에
a.compareTo(b)< b>일 경우 음의 값을 반환한다.a.compareTo(b)a = b인 경우 0을 반환함a.compareTo(b)a > b일 경우 양의 값을 반환한다.
중간에서 체크하는 것을 제외하고 간격을 검색하는 코드는 유사하다.
// 이 노드 확인 만일 (n.getKey().겹치다와 함께(i)) 결과.덧셈을 (n.getKey()); overlapsWith()다음과 같이 정의된다.
공중의 부울 겹치다와 함께(간격 타사의) { 돌아오다 출발하다.비교(타사의.getEnd()) <= 0 && 종지부를 찍다.비교(타사의.getStart()) >= 0; } 상위 치수
증강 나무는 나무의 각 레벨에서 치수를 순환함으로써 더 높은 차원으로 확장될 수 있다.예를 들어, 2차원의 경우 트리의 홀수 수준은 x 좌표에 대한 범위를 포함하고 짝수 수준은 y 좌표에 대한 범위를 포함할 수 있다.이 접근방식은 데이터 구조를 증강 바이너리 트리에서 증강 kd 트리로 효과적으로 변환하여 삽입 및 삭제에 대한 밸런싱 알고리즘을 상당히 복잡하게 한다.
더 간단한 해결책은 내포된 간격 트리를 사용하는 것이다.먼저 y 좌표 범위를 사용하여 트리를 생성하십시오.이제 트리의 각 노드에 대해 y 범위가 해당 노드의 y 범위와 동일한 모든 요소에 대해 x 범위 위에 다른 간격 트리를 추가하십시오.
이 솔루션의 장점은 동일한 코드베이스를 사용하여 임의의 치수까지 확장할 수 있다는 것이다.
처음에는, 중첩된 나무의 추가 비용이 엄청나게 들 것 같지만, 이것은 보통 그렇지 않다.앞의 비중첩 솔루션과 마찬가지로 x-코디네이트당 하나의 노드가 필요하며, 두 솔루션에 대해 동일한 수의 노드를 산출한다.유일한 추가 오버헤드는 중첩된 트리 구조의 오버헤드(수직 간격당 1개)이다.이 구조는 대개 무시할 수 있는 크기로, 루트 노드에 대한 포인터로만 구성되며, 아마도 노드의 수와 트리의 깊이로 구성된다.
내부 또는 길이 지향 트리
내선 또는 길이 지향 트리는 증원 트리와 유사하지만 대칭이며, 간격의 내선 점에 의해 순서가 정렬된다.간격의 길이(또는 길이의 절반)로 정렬된 모든 노드에는 최대 지향의 이진 힙이 있다.또한 각 노드(대칭)에 하위 트리의 최소값과 최대값을 저장한다.
오버랩 테스트
= 1 {\ i}에 대해두 간격의 시작 및 끝 값만 사용하여 다음과 같이 중복 테스트를 수행할 수 있다
< 및 > 0
이 값은 총액과 차액을 사용하여 단순화할 수 있다.
오버랩 테스트를 다음과 같이 줄인다.
간격 추가
트리에 새 간격을 추가하는 것은 내부 값을 키로 사용하는 이진 검색 트리의 경우와 동일하다. 를 노드와 연결된 이진 힙에 푸시하고, 모든 상위 노드와 관련된 가능한 최소값과 최대값을 업데이트한다.
겹치는 모든 구간 검색
쿼리 간격에는 d 을 사용하고 노드의 키( 과)에는 M displaystystylem M_을 사용합시다.
루트 노드부터 시작하여 각 노드에서 먼저 노드의 최소 및 최대 값을 사용하여 노드 하위 트리와 쿼리 간격이 중복될 수 있는지 확인하십시오(그렇지 않으면 이 노드에 대해 계속 진행하지 않음).
그런 다음 이 노드(자녀가 아님) 내부 간격이 간격과 겹치도록 { 을(를) 계산한다( i = M{\
d 보다 큰 { i에 대한 이진 힙에 대한 쿼리를 수행하십시오.
그리고 나서 우리는 같은 일을 하면서 그 노드의 왼쪽과 오른쪽 아이들을 통과한다.
최악의 경우 바이너리 검색 트리의 모든 노드를 검색해야 하지만 바이너리 힙 쿼리가 최적이기 때문에 허용된다(2차원 문제는 두 차원 모두에서 최적일 수 없음)
이 알고리즘은 검색 작업을 위한 기존 인터벌 트리(증강 트리)보다 빠를 것으로 예상된다.성장의 순서는 같지만 원소를 추가하는 것은 실제로는 조금 더딘 편이다.
참조
- ^ https://personal.us.es/almar/cg/08windowing.pdf[bare URL PDF]
- ^ a b 젠스 M. 슈미트작은 정수 범위의 간격 찌르기 문제.DOI. IACH09, 2009
- ^ 범위 쿼리#세미그룹 운영자
- 마크 드 버그, 마크 판 크레벨드, 마크 오버마르스, 오트프리드 슈바르츠코프.Computing Geometric, 2차 개정판.스프링거-베를라그 2000.제10.1절: 간격 나무, 페이지 212–217.
- Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009), Introduction to Algorithms (3rd ed.), MIT Press and McGraw-Hill, ISBN 978-0-262-03384-8
- 프랑코 P. 프리파타와 마이클 이안 샤모스.Computing Geometry: 소개.스프링거-베를라크, 1985년
외부 링크
- CGAL : C++의 연산지오메트리 알고리즘 라이브러리(Computer Geometry Algorithm Library)는 레인지 트리의 강력한 구현을 포함하고 있다
- Boost.Icl은 Interval 세트와 맵의 C++ 구현을 제공한다.
- IntervalTree(Python) - AVL 밸런싱이 있는 중앙 간격 트리, 태그 지정된 간격과 호환 가능
- Interval Tree(C#) - AVL 밸런싱이 있는 증강된 Interval Tree
- Interval Tree(Rubby) - 중심 구간 트리, 불변성, 태그 지정된 구간과 호환 가능
- IntervalTree(Java) - AVL 밸런싱, 중첩, 찾기, 수집 인터페이스, ID 관련 간격 지원, 증강 간격 트리

 집합의 구간 수입니다.쿼리는 모든 간격을 반환할 수 있으므로, 예를 들어 쿼리가 수집의 모든 간격을 교차하는 큰 간격인 경우 이는
집합의 구간 수입니다.쿼리는 모든 간격을 반환할 수 있으므로, 예를 들어 쿼리가 수집의 모든 간격을 교차하는 큰 간격인 경우 이는 





























 )에는 M
)에는 M 




