라딕스 트리

Radix tree
라딕스 트리의 예

컴퓨터 과학에서 라딕스 트리(Radix trie 또는 콤팩트한 접두사 트리)는 유일한 자식인 각 노드가 부모와 병합되는 공간에 최적화된 트리(prefix tree)를 나타내는 데이터 구조다.그 결과, 모든 내부 노드의 자식 수가 기껏해야 라딕스 트리의 라딕스 r이며, 여기서 r은 양의 정수이고, 힘 x는 2이고, x ≥ 1이다.일반 나무와 달리 가장자리에는 단일 원소뿐 아니라 원소 순서도 표기할 수 있다.이것은 라딕스 트리를 작은 집합(특히 문자열이 긴 경우)과 긴 접두사를 공유하는 문자열 집합에 훨씬 더 효율적이게 만든다.

일반 트리(전체 키를 처음부터 불평등 지점까지 일괄적으로 비교하는 경우)와는 달리, 각 노드의 키는 그 노드의 해당 청크에 있는 비트의 양이 라딕스 3의 라딕스 r이 되는 비트 단위로 비트 청크를 비교한다.r이 2일 때, radix trie는 이진수(즉, 그 노드의 키의 1비트 부분을 비교)로, trie 깊이를 최대화하는 비용(즉, 키에서 전달되지 않는 비트 스트링의 최대값)으로 스패시성을 최소화한다.r이 r ≥ 4를 갖는 2의 정수인 경우, r ix 3e는 r-arry 3e로, 잠재적인 sparsity를 희생시키면서 r ix 3e의 깊이를 감소시킨다.

최적화로서 엣지 라벨은 문자열(첫 번째 요소와 마지막 요소의 경우)에 대한 두 개의 포인터를 사용하여 일정한 크기로 저장할 수 있다.[1]

이 글의 예는 문자열을 문자의 시퀀스로 나타내지만, 문자열 요소의 유형은 임의로 선택할 수 있다는 점에 유의하십시오. 예를 들어 멀티바이트 문자 인코딩이나 유니코드를 사용할 때 문자열 표현의 비트 또는 바이트로 선택할 수 있다.

적용들

라딕스 트리는 문자열로 표현할 수 있는 키와 연관 배열을 구성하는 데 유용하다.그들은 몇 가지 예외를 가진 많은 범위의 값을 포함하는 능력이 특히 IP 주소의 계층적 구성에 적합한 IP 라우팅 영역에서 특별한 응용 프로그램을 찾는다.[2][3][4][5]정보 검색 시 텍스트 문서의 반전 색인에도 사용된다.

운영

Radix 트리는 삽입, 삭제, 검색 작업을 지원한다.삽입은 저장된 데이터 양을 최소화하면서 트라이에 새 문자열을 추가한다.삭제하면 트라이에서 문자열이 제거된다.검색 작업에는 정확한 검색, 전임자 찾기, 후임자 찾기, 접두사가 있는 모든 문자열이 포함된다(그러나 반드시 이에 국한되지는 않는다).이 모든 연산은 O(k)이며 여기서 k는 집합에 있는 모든 문자열의 최대 길이이며, 길이는 라디ix 3의 라디스와 동일한 비트 양으로 측정된다.

찾다

Patricia 3에서 문자열 찾기

조회 연산은 3진수에 문자열이 존재하는지 여부를 결정한다.대부분의 운영은 특정 업무를 처리하기 위해 어떤 방식으로든 이 접근방식을 수정한다.예를 들어, 문자열이 종료되는 노드가 중요할 수 있다.이 연산은 일부 에지가 여러 원소를 소비한다는 점을 제외하면 시도와 유사하다.

다음의 사이비 코드는 이러한 클래스가 존재한다고 가정한다.

가장자리

  • 노드 대상노드
  • 끈 레이블

노드

  • 모서리 모서리 배열
  • 함수 isLeaf()
기능{을 끓여뿌리에 없는 요소 노드 traverseNode:=뿌리 발견한 것과 시작하세요;elementsFound:=0int, 트래버스//까지 잎 또는는 동안(traverseNode!)null&&.!traverseNode.isLeaf()및 계속할 수 없다 발견된다;&elementsFound<>x.length){을 끓여lookup(문자열))연극에 가는 다음 가장자리다.plore에 따라x Edge nextEdge에서 아직 찾을 수 없는 요소:= traversNode.edge에서 edge 선택 여기서 edge.label이 x.suffix(elementsFound) // x.suffix(elementsFound)의 접두사인 x //의 마지막(x.length - elementsFound) 요소를 반환하는지 여부(다음 노드에서 탐색하도록 설정seNode := nextEdge.targetNode; // 에지 요소에 저장된 레이블을 기반으로 검색된 증가 요소Found += nextEdge.label.length; } 다른 { // 루프 트래버스 노드 종료 :=null; } // 잎 노드에 도착하여 u가 있으면 일치 항목이 발견됨정확히 x.length 요소 return (traversNode != null &&&traversNode.isLeaf() &&gt; found == x.length); }

삽입

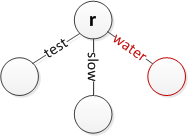
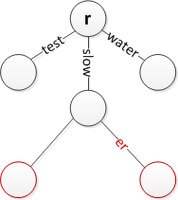
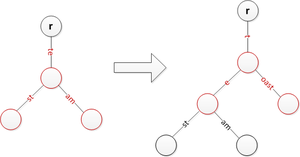
줄을 삽입하기 위해, 우리는 더 이상 진전되지 않을 때까지 나무를 뒤진다.이때 입력 문자열에 남아 있는 모든 요소가 레이블로 표시된 새 송신 에지를 추가하거나, 나머지 입력 문자열과 접두사를 공유하는 송신 에지가 이미 있는 경우, 이를 두 에지(공통 접두사로 레이블이 지정된 첫 번째)로 나누고 계속 진행하십시오.이 분할 단계를 통해 노드가 가능한 문자열 요소보다 더 많은 하위 요소를 가지지 않도록 보장한다.

더 많은 삽입 사례가 있을 수 있지만, 아래에 몇 가지 사례가 나와 있다.r은 단순히 루트를 나타낸다는 점에 유의하십시오.필요한 경우 문자열을 종료하기 위해 가장자리에 빈 문자열을 표시할 수 있으며 루트에 들어오는 가장자리가 없다고 가정한다.(빈 문자열 에지를 사용할 경우 위에서 설명한 조회 알고리즘이 작동하지 않음)

  • 뿌리에 '물' 삽입

  • '저속'을 유지하면서 '저속'을 삽입하십시오.

  • '테스터'의 접두사인 'test' 삽입

  • '테스트'를 분할하고 새 가장자리 레이블 'st'를 만드는 동안 '팀'을 삽입하십시오.

  • 'te'를 분할하고 이전 문자열을 한 수준 아래로 이동하면서 'toast'를 삽입하십시오.

삭제

나무에서 문자열 x를 삭제하려면 먼저 x를 나타내는 잎을 찾는다.그런 다음 x가 존재한다고 가정하면 해당 리프 노드를 제거한다.만약 우리의 잎 노드의 부모에게 다른 아이가 하나만 있다면, 그 아이의 수신 라벨은 부모의 수신 라벨에 추가되고 아이는 제거된다.

추가 작업

  • 공통 접두사가 있는 모든 문자열 찾기: 동일한 접두사로 시작하는 문자열 배열을 반환하십시오.
  • 이전 버전 찾기:주어진 문자열보다 작은 문자열의 가장 큰 문자열의 위치를 사전순으로 지정하십시오.
  • 후임자 찾기:주어진 문자열보다 큰 문자열의 가장 작은 문자열의 위치를 사전순으로 지정하십시오.

역사

데이터 구조는 1968년에 Donald R에 의해 발명되었다.주로 관련된 모리슨,[6] 그리고 제르노트 그웬버거에 의해.[7]

The Art of Computer Programming의 제3권 498-500쪽에 있는 도널드 크누스는 모리슨의 논문 제목인 "PATRICIA - Alphanumeric로 암호화된 정보를 검색하는 실용적인 알고리즘"의 약자 뒤에 이러한 것들을 "Patricia's trees"라고 부른다.오늘날 패트리샤는 라디ix 트리가 2와 같은 것으로 보여지는데, 이는 키의 각 비트가 개별적으로 비교되고 각 노드가 양방향(즉, 왼쪽 대 오른쪽) 분기라는 것을 의미한다.

다른 데이터 구조와의 비교

(다음 비교에서 키의 길이는 k이고 데이터 구조에는 n 멤버가 포함된다고 가정한다.)

균형이 잡힌 나무와 달리 라딕스 트리는 O(log n)가 아닌 O(k) 시간에 조회, 삽입, 삭제를 허용한다.이는 일반적으로 k log log n이므로 장점으로 보이지는 않지만, 균형 잡힌 트리에서 모든 비교는 O(k) 최악의 시간을 요구하는 문자열 비교로, 많은 비교는 긴 공통 접두사 때문에 실행 속도가 느리다(스트링 시작에서 비교가 시작되는 경우).3분의 1에서, 모든 비교는 일정한 시간을 필요로 하지만, 길이 m의 줄을 찾는 데는 m 비교가 필요하다.Radix 트리는 이러한 작업을 더 적은 비교로 수행할 수 있으며, 더 적은 수의 노드를 필요로 한다.

그러나 라딕스 트리는 시도에서 단점을 공유한다. 즉, 문자열의 효율적인 되돌릴 수 있는 매핑을 통해 요소나 요소의 문자열에만 적용할 수 있기 때문에 전체 순서가 있는 모든 데이터 유형에 적용되는 균형 잡힌 검색 트리의 전체 일반성이 결여되어 있다.문자열의 가역적 매핑은 균형 잡힌 검색 트리에 필요한 전체 순서를 생성하는 데 사용될 수 있지만, 다른 방법은 사용할 수 없다.이는 데이터 형식이 비교 연산만 제공할 뿐 (삭제)시리얼화 연산은 제공하지 않는 경우에도 문제가 될 수 있다.

해시 테이블은 일반적으로 예상 O(1) 삽입 및 삭제 시간을 가졌다고 하지만, 이는 키의 해시 연산을 상수 시간 연산으로 고려할 때에만 해당된다.키 해싱을 고려할 때 해시 테이블은 O(k) 삽입 및 삭제 시간이 예상되지만 최악의 경우 충돌 처리 방법에 따라 시간이 더 걸릴 수 있다.라딕스 트리는 최악의 경우 O(k) 삽입과 삭제가 가능하다.라딕스 트리의 후속/프로세서 운영도 해시 테이블에 의해 구현되지 않는다.

변형

라딕스 트리의 공통 확장에는 '검은색'과 '흰색'이라는 두 가지 색상의 노드가 사용된다.지정된 문자열이 트리에 저장되어 있는지 확인하기 위해 검색은 위에서 시작하여 더 이상 진행되지 않을 때까지 입력 문자열의 가장자리를 따른다.검색 문자열이 소비되고 최종 노드가 검은색 노드인 경우 검색이 실패하고 흰색 노드가 있으면 검색이 성공한 것이다.이를 통해 흰색 노드를 사용하여 트리에 공통 접두사가 있는 광범위한 문자열을 추가한 다음, 블랙 노드를 사용하여 작은 세트의 "예외"를 삽입하여 공간 효율적으로 제거할 수 있다.

HAT 트리(HAT-trie)는 효율적인 문자열 저장 및 검색과 순서 반복을 제공하는 라딕스 트리를 기반으로 한 캐시 의식 데이터 구조다.시간과 공간 모두에서 성능은 캐쉬를 의식한 해시테이블과 비교해도 손색이 없다.[8][9][1]의 HAT 3e 구현 참고 사항 참조

PATRICIA trie는 모든 키의 모든 비트를 명시적으로 저장하기 보다는 노드가 두 개의 하위 트리를 구분하는 첫 번째 비트의 위치만 저장하는 라딕스 2 (이진) 트리의 특별한 변형이다.순회하는 동안 알고리즘은 검색 키의 인덱싱된 비트를 검사하고 적절하게 왼쪽 또는 오른쪽 하위 트리를 선택한다.PATRICIA trie의 주목할 만한 특징으로는 저장되는 모든 고유 키에 대해 trie가 한 개의 노드만 삽입하면 PATRICIA가 표준 이진 trie보다 훨씬 콤팩트해진다는 점이 있다.또한 실제 키는 더 이상 명시적으로 저장되지 않기 때문에 일치 여부를 확인하기 위해 인덱싱된 레코드에서 전체 키 비교를 한 번 수행해야 한다.이 점에서 PATRICIA는 해시 테이블을 사용한 인덱싱과 어느 정도 유사하다.[10]

적응형 라딕스 트리는 적응형 노드 크기를 라딕스 트리에 통합한 라딕스 트리 변형이다.일반적인 라딕스 트리의 주요한 단점은 모든 레벨에서 일정한 노드 크기를 사용하기 때문에 공간의 사용이다.라딕스 트리와 적응형 라딕스 트리의 주요 차이점은 새로운 항목을 추가하면서 증가하는 하위 요소의 수에 따른 각 노드의 가변 크기다.따라서 적응형 라딕스 트리는 속도를 줄이지 않고 공간을 더 잘 사용하도록 이끈다.[11][12][13]

일반적인 관행은 부모가 데이터 집합에서 유효한 키를 나타내는 상황에서 자녀가 한 명인 부모를 허용하지 않는 기준을 완화하는 것이다.이 라딕스 트리의 변형은 최소 두 개의 자식 노드가 있는 내부 노드만 허용하는 것보다 높은 공간 효율을 달성한다.[14]

참고 항목

참조

  1. ^ Morin, Patrick. "Data Structures for Strings" (PDF). Retrieved 15 April 2012.
  2. ^ "rtfree(9)". www.freebsd.org. Retrieved 2016-10-23.
  3. ^ The Regents of the University of California (1993). "/sys/net/radix.c". BSD Cross Reference. NetBSD. Retrieved 2019-07-25. Routines to build and maintain radix trees for routing lookups.
  4. ^ "Lockless, atomic and generic Radix/Patricia trees". NetBSD. 2011.
  5. ^ 크니즈니크, 콘스탄틴.2008년 6월 Dobb's Journal, "Patricia Trys: A Better Index For Prefix Searchs".
  6. ^ 모리슨, 도널드 R. PATRICIA - 영숫자로 코딩된 정보를 검색하는 실용적인 알고리즘
  7. ^ G. Gweenberger, Anwendung einer bineren Verweisketenmethode beim Aufbau von Listen.엘렉트로니셰 레케난라겐 10(1968), 페이지 223–226
  8. ^ Askitis, Nikolas; Sinha, Ranjan (2007). HAT-trie: A Cache-conscious Trie-based Data Structure for Strings. Proceedings of the 30th Australasian Conference on Computer science. Vol. 62. pp. 97–105. ISBN 1-920682-43-0.
  9. ^ Askitis, Nikolas; Sinha, Ranjan (October 2010). "Engineering scalable, cache and space efficient tries for strings". The VLDB Journal. 19 (5): 633–660. doi:10.1007/s00778-010-0183-9.
  10. ^ 모리슨, 도널드 R.영숫자로 코딩된 정보를 검색하기 위한 실제 알고리즘
  11. ^ Kemper, Alfons; Eickler, André (2013). Datenbanksysteme, Eine Einführung. Vol. 9. pp. 604–605. ISBN 978-3-486-72139-3.
  12. ^ "armon/libart: Adaptive Radix Trees implemented in C". GitHub. Retrieved 17 September 2014.
  13. ^ http://www-db.in.tum.de/~leis/paper/ART.pdf
  14. ^ 유효한 키를 나타내는 Radix 트리의 노드가 하나의 자식을 가질 수 있는가?

외부 링크

구현