델타 시그마 변조

사인파(빨간색)의 1비트 델타 변조(파란색).

델타 시그마 변조는 델타 시그마 아날로그-디지털 변환기(ADC) 및 디지털-아날로그 변환기(DAC) 프로세스의 일부로 매우 높은 샘플 주파수에서 낮은 비트 깊이의 디지털 신호로 신호를 인코딩하기 위한 오버샘플링 방법입니다.델타-시그마 변조는 양자화 중에 음의 피드백 루프를 이용하여 낮은 비트 깊이까지 지속적으로 양자화 오류를 수정하고 양자화 노이즈를 원래 신호의 대역폭보다 훨씬 높은 주파수로 이동시킴으로써 고품질을 달성합니다.복조를 위한 후속 저역 통과 필터링은 이러한 고주파 노이즈와 시간 평균을 쉽게 제거하여 진폭의 높은 정확도를 달성합니다.

ADC와 DAC 모두 델타 시그마 변조를 사용할 수 있습니다.델타 시그마 ADC(예: 그림 1 상단)는 고주파 델타 시그마 변조를 사용하여 아날로그 신호를 인코딩한 다음 디지털 필터를 적용하여 더 낮은 샘플링 주파수의 높은 비트 디지털 출력에 복조합니다.델타 시그마 DAC(예: 그림 1 하단)는 고해상도 디지털 입력 신호를 저해상도이지만 더 높은 샘플 주파수 신호로 인코딩하여 전압에 매핑하고 복조를 위해 아날로그 필터로 평활화할 수 있습니다.두 경우 모두 높은 샘플링 주파수에서 낮은 비트 깊이 신호를 일시적으로 사용하면 회로 설계가 단순화되고 디지털 전자 장치의 시간 효율과 높은 정확도를 활용할 수 있습니다.

주로 비용 효율성과 감소된 회로 복잡성 때문에 이 기술은 DAC, ADC, 주파수 신시사이저, 스위치 모드 전원 공급 장치 및 모터 ^[1]제어기와 같은 현대 전자 부품에서 점점 더 많이 사용되고 있습니다.델타 시그마 ADC의 대략적으로 양자화된 출력은 때때로 신호 처리에 직접 사용되거나 신호 저장을 위한 표현으로 사용됩니다(예: 슈퍼 오디오 CD는 1비트 델타 시그마 변조기의 원시 출력을 저장합니다).

동기

아날로그 신호를 직접 전송할 때 시스템 및 전송의 모든 노이즈가 아날로그 신호에 추가되어 품질이 저하됩니다.디지털화하면 노이즈가 없는 전송, 저장 및 처리가 가능합니다.디지털화에는 여러 가지 방법이 있습니다.

나이키스트 레이트 ADC에서 아날로그 신호는 나이키스트 레이트 바로 위의 상대적으로 낮은 샘플링 주파수(신호의 가장 높은 주파수의 두 배)에서 샘플링되고 멀티 레벨 양자화기에 의해 양자화되어 멀티비트 디지털 신호를 생성합니다.이러한 고비트 방법은 직접 진폭의 정확도를 추구하지만 매우 정밀한 구성 요소가 필요하므로 선형성이 저하될 수 있습니다.

오버샘플링의 장점

오버샘플링 변환기는 훨씬 높은 샘플링 주파수에서 낮은 비트 깊이 결과를 생성합니다.이는 다음과 같은 이점을 활용하여 비슷한 품질을 달성할 수 있습니다.

더 높은 정확도의 시간(고속 디지털 회로 및 매우 정확한 시계 제공)
저비트 ADC 및 DAC에 의해 제공되는 더 높은 선형성(예: 정밀한 고전압과 정밀한 저전압의 두 값만 출력하는 1비트 DAC는 원칙적으로 완벽하게 선형입니다).
노이즈 쉐이핑: 관심 신호보다 높은 주파수로 노이즈를 이동하여 로우패스 필터링으로 쉽게 제거할 수 있습니다.
아날로그 로우패스 앤티앨리어싱 필터의 경사도 요구사항 감소.평평한 통과 대역이 있는 고차 필터는 디지털 도메인보다 아날로그 도메인에서 만드는 데 더 많은 비용이 듭니다.

주파수/해상도 트레이드오프

오버샘플링이 제공하는 또 다른 주요 측면은 주파수/해상도 트레이드오프입니다.변조기 뒤에 배치되는 소멸 필터는 전체 샘플링 신호를 관심 대역에서 필터링할 뿐만 아니라(높은 주파수에서 노이즈를 차단함), 샘플링 속도와 신호의 대표적인 주파수 범위를 감소시키는 동시에 샘플 진폭 분해능을 높입니다.이러한 진폭 분해능 향상은 데이터 속도가 더 높은 비트 스트림의 평균화를 통해 얻을 수 있습니다.

델타 변조 대비 개선

델타 시그마 변조는 저비트 오버샘플링 방법의 한 유형입니다.음의 피드백도 사용하는 이전의 관련 방법을 델타 변조라고 합니다.델타 변조는 진폭이 아닌 신호의 변화(델타)만 인코딩합니다.결과는 펄스 코드 변조(PCM)의 경우와 같은 진폭 숫자의 스트림과 반대로 위 또는 아래를 나타내는 펄스 스트림입니다.

델타 변조는 미분을 나타내기 때문에 DC 성분을 전달할 수 없으며 동적 범위와 SNR은 신호 주파수에 반비례하며, 누적 오류를 초래하는 전송 방해에 취약합니다.델타 시그마 변조는 적분기와 양자화기의 위치를 재정렬하여 출력이 단순히 도함수가 ^[2]아닌 입력 신호의 진폭에 해당하는 정보를 전달하도록 합니다.이는 또한 변환 프로세스에 바람직한 노이즈 쉐이핑을 통합하여 의도적으로 양자화 노이즈를 신호보다 높은 주파수로 이동시키는 이점이 있습니다.

1비트 델타 변조는 펄스 밀도 변조입니다.

단일 비트 델타 시그마 ADC의 경우 아날로그 전압 신호는 펄스 주파수 또는 펄스 밀도로 효과적으로 변환되며, 이는 PDM(pulse-density modulation)으로 이해될 수 있습니다. 알려진 고정 속도로 비트를 나타내는 일련의 양 및 음의 펄스는 생성, 전송 및 정확한 재생이 매우 쉽습니다.펄스의 타이밍과 신호를 복구할 수 있는 경우에만 수신기에서.델타 시그마 변조기에서 이러한 일련의 펄스가 발생하면 원래 파형을 적절한 정밀도로 재구성할 수 있습니다.

신호 표현으로 PDM을 사용하는 것은 펄스 코드 변조(PCM)의 대안입니다. 또는 고주파 PDM은 나중에 decimation이라고 하는 처리를 통해 다운샘플링되고 관심 주파수 대역의 Nyquist 속도에 가까운 낮은 샘플링 주파수에서 멀티비트 PCM 코드로 변환되도록 재할당될 수 있습니다.

역사와 변주곡

델타 변조를 달성하기 위해 피드백과 오버샘플링을 결합한 중요한^[3] 논문은 1952년 ^[4]Philips Research Laboratory의 F. de Jager에 의해 작성되었습니다.

델타-시그마 변환의 기본 원리인 피드백을 사용하여 거친 양자화기의 해상도를 향상시키는 원리는 C에 의해 1954년에 출원된 특허에서 처음 설명되었습니다. 벨 ^[5]연구소의 채핀 커틀러입니다.1962년^[6] 도쿄 대학의 이노세 등이 델타 ^[7]^{[note 1]}변조기의 전진 경로에 필터를 추가하는 아이디어를 생각해 내기 전까지는 그렇게 명명되지 않았습니다.

Woley의 "Oversampling Analog-to-Digital Converters"^[3]는 더 많은 역사와 관련 특허에 대한 참조를 제공합니다.변조기의 순서, 양자화기의 비트 깊이, 소멸 방법, 오버샘플링 비율 등 다양한 변동 방법이 있습니다(여러 조합으로 적용될 수 있음).

고차 변조기

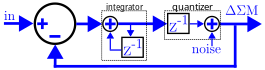
노이즈 쉐이핑은 Δ 변조기의 순서를 나타내는 여러 통합기 단계를 계단식으로 연결함으로써 개선됩니다(예: 그림 2는 2차^nd 변조기).

1차^st 변조기는 무조건 안정적이지만, 고차 노이즈 제거 변조기에 대해서는 안정성 분석을 수행해야 합니다.또는 노이즈 피드포워드 구성은 항상 안정적이며 ^[8]^§6.1분석이 단순합니다.

멀티비트 양자화기

변조기는 양자화기의 비트 깊이로 분류할 수도 있습니다.N-수준을 구분하는 양자화기를 logN₂ 비트 양자화기라고 합니다.예를 들어, 단순 비교기에는 레벨이 2개 있고 1비트 양자화기도 마찬가지입니다. 3레벨 양자화기는 "1.5"비트 양자화기, 4레벨 양자화기는 2비트 양자화기,^[9] 5레벨 양자화기는 2.5비트 양자화기라고 합니다.비트 양자화기가 높을수록 본질적으로 양자화 노이즈가 줄어듭니다.

1비트 양자화에 대한 한 가지 비판은 피드백 루프에서 적절한 양의 디터를 사용할 수 없으므로 일부 조건에서 왜곡이 들릴 수 있다는 것입니다(Direct Stream Digital § DSD vs. PCM에서 ^[10]^[11]더 많은 논의).

후속 소멸

소멸은 델타-시그마 변조와 강하게 관련되어 있지만, 구별되고 이 기사의 범위 밖입니다.1962년 원본 논문은 멸종에 대해 설명하지 않았습니다.초기에 오버샘플한 데이터는 그대로 보냈습니다.과도하게 샘플링된 델타 시그마 데이터를 PCM 오디오로 변환하기 전에 디지털 필터링을 사용하여 소멸시키자는 제안은 ^[12]1969년 Bell Labs의 D. J. Goodman이 높은 샘플링 속도에서 Δ 신호를 줄이고 비트 깊이를 증가시키기 위해 제안했습니다.소멸은 델타 시그마 비트 스트림의 수신단에 있는 별도의 칩에서 수행될 수 있으며, 많은 Δ ADC 집적 회로가 소멸을 포함하지만 PDM MEMS ^[14]마이크와의 인터페이스에 유용한 마이크로컨트롤러 ^[13]내부의 전용 모듈에 의해 수행될 수 있습니다.일부 마이크로컨트롤러에는 변조기와 소멸기가 ^[15]모두 포함되어 있습니다.

Δ ADC에 가장 일반적으로 사용되는 소멸 필터는 복잡성과 품질을 증가시키는 순서로 다음과 같습니다.

Boxcar 이동 평균 필터(단순 이동 평균 또는 동기 주파수 필터)는 더 큰 샘플링 간격 동안 얼마나 많은 샘플이 높은지 간단히 계산하여 구현할 수 있습니다.이것은 매우 조잡하지만 단순하지만, 상호 변조 왜곡을 겪고 고주파 노이즈를 감쇠시키는 데는 보통 수준의 작업만 수행합니다.또 다른 Bell Labs 연구원인 J. Candy의 1974년 논문 "강력한 아날로그-디지털 ^[16]변환기를 얻기 위한 제한 주기 진동 사용"은 이것의 초기 예 중 하나였습니다.
계단식 적분기-콤브 필터.이러한 필터를 sinc 필터라고 하며^N, 위의 sinc-in-frequency 필터(sinc¹ 필터로 간주될 수 있음)를 n번 계단식으로 연결하는 것과 같습니다.N 필터가 낮을수록 간단하고 빠르게 안착하며 기본 대역의 감쇠가 적은 반면 N 필터가 낮을수록 약간 더 복잡하고 느리게 안착하지만 원하지 않는 고주파 노이즈를 더 잘 감쇠시킵니다.
- 많은 Δ ADC는 2차^nd 5단계 동기³ 델타 시그마 구조를 사용합니다.2차^nd 변조기의 경우 동기³ 필터가 ^[17]^[18]최적에 가깝습니다.
동기식(주파수의 벽돌벽) 필터입니다.이것은 최고 품질의 변환기(현재는 고해상도 디지털 오디오의 사실상 표준)에서 사용됩니다.낮은 주파수 관심 대역의 감쇠 없이 거의 모든 원하지 않는 고주파 노이즈를 제거하지만, 동기 함수는 고유한 지연으로 인해 어려움을 겪습니다.sinc 함수가 음의 무한대에서 양의 무한대로 확장되므로 물리적으로 유한한 시간 내에 가능하지 않기 때문에 sinc-in-time 필터는 근사치만 계산할 수 있습니다.

오버샘플링 비율 및 ΔM 순서를 높여 베이스밴드 노이즈 감소

신호가 양자화될 때, 결과 신호는 전체 스펙트럼에 걸쳐 거의 동일한 강도를 갖는 백색 노이즈를 추가하여 근사할 수 있습니다.실제로 양자화 노이즈는 물론 신호와 독립적이지 않으며 이러한 의존성은 한계 주기를 초래하며 델타 시그마 변환기에서 유휴 톤과 패턴 노이즈의 원인입니다.그러나 디더링 노이즈(그림 3)를 추가하면 양자화 노이즈가 더 랜덤하게 되어 이러한 왜곡이 줄어듭니다.

Δ ADC는 기저 대역에서 노이즈를 분산시키고 대부분 높은 주파수로 형성함으로써 노이즈의 양을 줄입니다.그런 다음 나이키스트 ADC에 필요한 고정밀 아날로그 회로 없이 저렴한 디지털 필터로 쉽게 필터링할 수 있습니다.

양자화 노이즈 확산을 위한 오버샘플링

베이스밴드 주파수 범위( $2f_{0}$ 에서 $({$ 의 양자화 노이즈는 다음과 같이 정의된 오버샘플링 비율(OSR)을 증가시켜 감소시킬 수 있습니다.

\mathrm {OSR} \,=\,{\frac {f_{0}}{2f_{0}}=2^{d}

$f_{\mathrm {s} }$ 서 $fs{$ displaystyle $f_{\mathrm {s}}$ 는 $f_{{\mathrm {s}}}$ 샘플링 $2f_{0}$ 이고 $($ 은 $2f_{0}$ 나이키스트 속도(원래 신호의 최대 $f_{0}$ $({$ 의 두 배)입니다.오버샘플링은 일반적으로 2의 거듭제곱으로 수행되므로 d ${displaystyled}$ 는 $d$ OSR이 두 배가 되는 횟수를 나타냅니다.

그림 4: 1, 2^nd, 3차^rd Ω 변조기의 노이즈^st 쉐이핑 곡선 및 노이즈 스펙트럼.

그림 4에 표시된 것처럼, 양자화 노이즈의 총 양은 Nyquist 컨버터(노란색 + 녹색 영역)와 오버샘플링 컨버터(파란색 + 녹색 영역) 모두에서 동일합니다.그러나 오버샘플링 변환기는 훨씬 더 넓은 주파수 범위에 노이즈를 분산시킵니다.이점은 관심 주파수 대역의 총 노이즈 양이 오버샘플링 변환기(작은 녹색 영역만)의 경우 나이키스트 변환기(노란색 + 녹색 영역)의 경우보다 훨씬 적다는 것입니다.

노이즈 셰이핑

그림 4는 Δ 변조가 어떻게 노이즈를 형성하여 더 높은 주파수(쉽게 걸러질 수 있는 주파수)에서 노이즈를 증가시키는 대신 베이스 밴드에서 양자화 노이즈의 양을 더욱 감소시키는지 보여줍니다.고차 Δ 변조기의 곡선은 기저 대역에서 훨씬 더 큰 노이즈 감소를 달성합니다.

이러한 곡선은 라플라스 변환(연속 시간 신호(예: ADC의 변조 루프) 또는 Z 변환(예: DAC의 변조 루프)이라고 하는 수학적 도구를 사용하여 도출됩니다.이러한 변환은 복잡한 ${\text{s}}=\sigma +j\omega$ ${\text{z}}=Ae^{j\phi }$ ${\text{s}}=\sigma +j\omega$ ${\text{z}}=Ae^{j\phi }$ + ${\text{s}}=\sigma +j\omega$ $디스플레이$ 스타일 $({texts}=\$ displaystyle + $j\omega}$ ${\text{z}}=Ae^{j\phi }$ z = ${\text{z}}=Ae^{j\phi }$ z}})의 복잡한 주파수 ${\text{z}}=Ae^{j\phi }$ 영역에서 시간 영역에서 더 어려운 수학을 더 간단한 수학으로 변환하는 데 유용합니다. $=Ae^{j\phi }}($ z-도메인에 있음).이러한 표기법은 디지털 신호 처리의 언어 단위이지만 일반인은 이해할 수 없습니다.

라플라스 영역에서의 Δ ADC 변조 루프 해석

그림 5는 라플라스 도메인에서 연속 시간 선형 시간 불변 시스템으로서의 ADC Δ 변조 루프(그림 1 참조)를 나타냅니다.시간 함수 통합의 라플라스 변환은 단순히 1s( $디스플레이$ 스타일 {\ $tfrac {1}{\text{s}}})$ 의 ${\tfrac {1}{\text{s}}}$ 곱셈이 되며 양자화 과정은 양자화 오류 노이즈 소스를 추가하여 근사화됩니다.양자화(신호 처리) § 가법적 노이즈 모델은 (특히 저비트 양자화의 경우) 항상 유효한 가정은 아님을 설명하지만 노이즈는 종종 신호와 무관하다고 가정합니다.그림 5의 라플라스 표기법에서의 변조 루프는 다음과 같습니다.

표시 스타일 [{\text{in}}({\text{s})-\Delta \Sigma {\text{M}({\text{s})}+{\text{noise}({\text{s})}=\Delta \Sigma \text{M}({\text{s})\text{\text}}\text{\text{\text}}}\text{\text}}\text{\text}}\text}\text}\text}\text

시스템과 라플라스 변환은 선형이므로 입력에 영향을 미치는 방식과 ^[8]^§6노이즈에 영향을 미치는 방식을 분리하여 이 시스템의 전체 동작을 분석할 수 있습니다.

디스플레이 스타일 \Delta \Sigma \텍스트M}_{\text{total}}({\text{s}})=\Delta \Sigma{text{M}_{\text{in}}({\text{s}})+\Delta \Sigma({text})M}_{\text{noise}}({\text{s}})\baem}

입력 시 로우패스 필터

시스템이 입력 신호에만 어떤 영향을 미치는지 이해하기 위해 노이즈는 일시적으로 0으로 추정됩니다.

{\text{in}}({\text{s})--\Delta \Sigma \text{M}_{\text{in}}({\text{s})]\cdot{frac{1}{\text}}}}+0=\Delta \Sigma \text{M}}_{\text{in}}({\text{s})\....}

다음과 같은 전송 기능을 제공하도록 재배열할 수 있습니다.

display style(*frac\Delta \Sigma 텍스트)M}_{\text{in}}({\text{s}})}{{\text{in}}({\text{s}})}={\textfrac{1}{\text{s}}}}={textfrac{1}{\text{s}}}}}{\{\textfrac{1}}{\text{\text{s}}}}}}}}\textfrac{\textfrac}}}}}

이 전송 함수는 s ${\text{s}}={\text{-1}}$ 에 ${\text{s}}={\text{-1}}$ 극을 갖습니다. { $displaystyle}{text$ $}}=$ 복잡한 평면에서 텍스트 ${-1}}$ 을 ${\text{s}}={\text{-1}}$ (를) 입력 신호에서 1차 로우패스^st 필터로 효과적으로 작용합니다.(참고: 루프에 상수에 의한 곱셈을 포함하여 컷오프 주파수를 원하는 대로 조정할 수 있습니다.)

하이패스 필터 온 노이즈

시스템이 소음에만 영향을 미치는 방식을 이해하기 위해 입력을 일시적으로 0으로 가정합니다.

표시 스타일 [0-\Delta \Sigma \text}M}_{\text{noise}}({\text{s})]\cdot{frac{1}{\text{s}}+{\text{noise}}({\text{s})=\Delta \Sigma{text{text}M}_{\text{noise}}({\text{s})\....}

다음과 같은 전송 기능을 제공하도록 재배열할 수 있습니다.

display style(*frac\Delta \Sigma 텍스트)M}_{\text{noise}}({\text{s}})}{{\text{noise}}({\text{s}})}={textfrac{1}{\text{s}}}}={\textfrac{s}}}{\textfrac{s}}}{\text{\text{\text{s}}}}}}}}}\timfrac{{\text}}}}}}}}}}\timeflamb}}}}\timfrac{

이 전송 함수는 s ${\text{s}}=0$ 에서 0이 하나입니다. {\ $displaystyle\texts$ $}}=0}$ 과 ${\text{s}}=0$ (와) s = ${\text{s}}={\text{-1}},$ 의 ${\text{s}}={\text{-1}},$ 극, ${\displaystyle\texts$ $}}=$ 임시 $텍스트{-1}},}$ 를 ${\text{s}}={\text{-1}},$ 사용하면 시스템이 DC에서 0에서 시작하여 차단 주파수에 도달할 때까지 점진적으로 상승한 다음 레벨 오프되는 노이즈에 대해 하이패스 필터 역할을 효과적으로 수행할 수 있습니다.

z-도메인에서의 Δ 변조 루프 해석

한편, Δ DAC의 변조 루프(그림 6)는 이산 시간에 있으므로 분석은 z 영역에 있습니다.이는 라플라스 영역의 위 분석과 매우 유사하며 유사한 곡선을 생성합니다.참고: 많은 소스는^[8]^§6.1^[19]^[20] 또한 z-도메인에서 Δ ADC의 변조 루프를 분석하며, 이는 지속적인 아날로그 입력을 이산 시간 신호로 암시적으로 처리합니다.입력 신호가 이미 대역 제한되어 있고 샘플링 속도보다 높은 시간 척도에서 변경되지 않는다고 가정할 수 있는 경우 이는 유효한 근사치일 수 있습니다.모듈레이터가 스위치형 캐패시터 회로로 구현되어 있는 경우 특히 적합하며, 이 회로는 클럭 시간 단계에서 캐패시터 간에 전하를 전송하여 작동합니다.

이산 시간의 적분은 입력 $x[n]$ [ $y[n]=x[n]+y[n-1].$ $]$ {{ $displaystyle$ x[ $n]}$ 를 $x[n]$ [ $y[n]=x[n]+y[n-1].$ $=$ [ $y[n]=x[n]+y[n-1].$ + $y[n]=x[n]+y[n-1].$ [ $y[n]=x[n]+y[n-1].$ - $y[n]=x[n]+y[n-1].$ ] $y[n]=x[n]+y[n-1].$ {\ $displaystyle y$ [n] = $x[$ n] + $y[$ . .} 이는 1클럭 사이클 지연 단계(z-1{text{z}^{\text{1}}로 표기)를 통해 summing 노드의 출력 y(z)({displaystyle y\text{z}})를 summing 노드의 다른 입력에 피드백하여 y(z) = x(z) + y(z) z-1{displaysty\text{z}}}{z}}}를 생성함으로써 z-displaysty 영역에 표현된다\ $cdot{text{z}}^{\$ $text$ ${-1$ 전송 ${\tfrac {1}{1-{\text{z}}^{\text{-1}}}}$ ${\tfrac {1}{1-{\text{z}}^{\text{-1}}}}$ - ${\tfrac {1}{1-{\text{z}}^{\text{-1}}}}$ - ${\tfrac {1}{1-{\text{z}}^{\text{-1}}}}$ 1 { $displaystyle{{text{z}}^{\$ text ${-1}}}$ 는 ${\tfrac {1}{1-{\text{z}}^{\text{-1}}}}$ 블록 다이어그램에서 적분기에 레이블을 지정하는 데 자주 사용됩니다 $.$

ΔDAC에서 양자화기는 이미 디지털 및 양자화된 입력이지만 단순히 더 높은 비트 깊이에서 더 낮은 비트 깊이의 디지털 신호로 감소하기 때문에 재양자화기 또는 DDC(Digital-to-Digital Converter)라고 불릴 수 있습니다.이것은 양자화 노이즈를 추가하는 일련의 또 ${\text{z}}^{\text{-1}}$ $({$ 지연 ${\text{z}}^{\text{-1}}$ 단계로 z-영역에서 나타납니다.(참고: 일부 소스는 $({$ 과 ${\text{z}}^{\text{-1}}$ 가법 노이즈 단계의 순서를 바꾸었을 수 있습니다.)

그림 6과 같이 배열된 변조기의 z-도메인 방정식은 다음과 같습니다.

표시 스타일 [{\text{in}}({\text{z})]-\Delta \Sigma \text{M}({\text{z})]\cdot {frac{1}{\text{z}}^{\text{-1}}}+{\text{noise}}=\Delta \Sigma {\text{M}(\text}}}}}...

출력을 입력 및 노이즈 측면에서 표현하도록 재배열할 수 있습니다.

\displaystyle \Delta \Sigma \Sigma \text{M}({\text{z})={text{in}({\text{z})\cdot{\text{z}}^{\text{noise}}+\cdot(1-{\text{z}})^{\text{\text{\text{1}}}}}\text{\text{\text{\text{\text{}}}}}}}}}}}}\text}}

입력은 단순히 하나의 클럭 사이클로 지연된 시스템에서 나옵니다.노이즈 용어의 (

(1-{\text{z}}^{\text{-1}})

-

(1-{\text{z}}^{\text{-1}})

-

(1-{\text{z}}^{\text{-1}})

1

){displaystyle (1-{\text

{z

}}^{\text{-1

{\text{z}}{=}1

에 의한

(1-{\text{z}}^{\text{-1}})

곱은 첫 번째 차이 역방향 필터(원점에 단일 극이 있고 z

= 1

에서

{\text{z}}{=}1

0이 있음)를

(1-{\text{z}}^{\text{-1}})

나타내므로 하이패스는 노이즈를 필터링합니다.

고차 변조기

수학적 ^[19]^{(equations 8-11)}세부 사항에 들어가지 않고 $\Theta ^{\text{th}}$ ${\displaystyle$ \ $Theta$ 적분기를 계단식으로 연결하여 $Δth{\$ displaystyle \ $Theta ^{\text{$ th}} - 순서 $\Theta ^{\text{th}}$ 변조기를 생성하면 다음과 같은 결과를 얻을 수 있습니다.

디스플레이 스타일 \Delta \Sigma \텍스트M}}_{\Theta}({\text{z})={text{in}}({\text{z}})\cdot{\text{z}}^{\text{z}}+{\text{noise}}\cdot(1-{\text{z}})^{\text{\text{\text{-1}}}})})^{\\\\\\\세타 }\bearn}

이 첫 번째 차이 역방향 필터는 이제

\displaystyle \Theta}

의

\Theta

검정력으로 상승하기 때문에 기저 대역에서 더 큰 감쇠의 특성을 개선하기 위해 더 가파른 노이즈 쉐이핑 곡선을 가질 것이며, 따라서 노이즈의 상당 부분이 기저 대역 위에 있으며 이상적인 저역 필터로 쉽게 필터링할 수 있습니다.

이론적 유효 비트 수

$(이상적$ 인 로우패스 디시메이션 필터를 사용하여 $2^{d}$ ) $\Theta ^{\text{th}}$ 이 있는 ${\$ $displaystyle$ $\Theta$ $^{\$ $text{$ $th$ $}}$ - 순서 $\Theta ^{\text{th}}$ 변조기를 통해 이동하는 정현파 입력에 대한 이론적 신호 대 잡음비(dB)는 대략 다음과 ^[19]^{(equations 12-21)}같이 수학적으로 도출될 수 있습니다.

스타일 표시({text})SNR}_{\text{dB}}\approx 3.01\cdot (2\cdot \Theta +1)\cdot d-9.36\cdot \Theta -2.76\baem}

따라서 이론적 유효 비트 수(ENOB) 분해능은 OSR을 두 배로 늘릴 때

{\textstyle \Theta +{\tfrac {1}{2}}}

{\textstyle \Theta +{\tfrac {1}{2}}}

({\textstyle

\

d

Theta +{\tfrac {1}{2}}

비트

{\textstyle \Theta +{\tfrac {1}{2}}}

, 순서를 늘릴 때

{\textstyle d-{\tfrac {3}{2}}}

-

({\

비트씩

{\textstyle d-{\tfrac {3}{2}}}

향상됩니다.비교를 위해 (노이즈 쉐이핑 없이) 나이키스트 ADC를 오버샘플링하면 OSR을 ^[21]두 배로 늘릴 때마다 ENOB가

{\tfrac {1}{2}}

향상됩니다

.

1차^st ΔM의 ENOB 증가율의 1⁄3.

이론적 SNR 및 ENOB 대 ΔM 순서 및 오버샘플링 비율(OSR)
	오버샘플링 비율					각 OSR 두 배로
	OSR 2개⁴	OSR 2개⁵	OSR 2개⁶	OSR 2개⁷	OSR 2개⁸	각 OSR 두 배로
1차^st:	24dB 3+3/4비트	33dB 5+1⁄4 비트	42dB 6+3/4비트	51dB 8+1⁄4 비트	60dB 9+3/4비트	+1+1⁄2 비트
2차^nd:	39dB 6+1⁄4 비트	54dB 8+3/4비트	69dB 11+1⁄4 비트	84dB 13+3/4비트	99dB 16+1⁄4 비트	+2+1⁄2 비트
3차^rd:	53dB 8+3/4비트	75dB 12+1⁄4 비트	96dB 15+3/4비트	117dB 19+1⁄4 비트	138dB 22+3/4비트	+3+1⁄2 비트
4차^th:	68dB 11+1⁄4 비트	95dB 15+3/4비트	112dB 20+1⁄4 비트	149dB 24+3/4비트	177dB 29+1⁄2 비트	+4+1⁄2 비트
5차^th:	83dB 13+1⁄2 비트	116dB 19비트	149dB 24+1⁄2 비트	182dB 30비트	215dB 35+1⁄2 비트	+5+1⁄2 비트
6차^th:	99dB 16비트	137dB 22+1⁄2 비트	176dB 29비트	215dB 35+1⁄2 비트	254dB 42비트	+6+1⁄2 비트
각 추가 주문:	+2+1⁄2 비트	+3+1⁄2 비트	+4+1⁄2 비트	+5+1⁄2 비트	+6+1⁄2 비트

이러한 데이터 포인트는 이론적입니다.실제로, 회로는 불가피하게 해상도를 제한하는 다른 노이즈 소스를 경험하여 녹색 셀을 비실용적으로 만듭니다.

델타 변조와의 관계

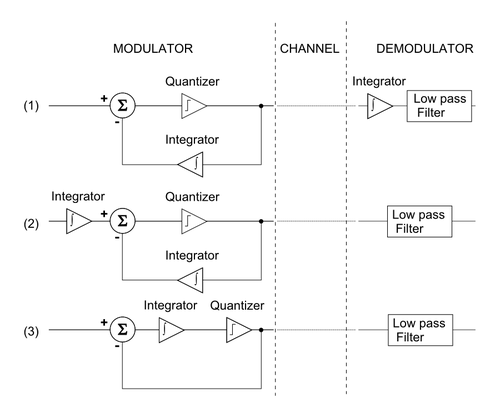
델타 시그마 변조는 다음 단계에 따라 델타 변조와 관련이 있습니다(그림 7).^[8]^§6

델타 변조기/복조기의 블록 다이어그램으로 시작합니다.
적분의 선형성 ${\textstyle \int a+\int b=\int (a+b)}$ 인 ${\textstyle \int a+\int b=\int (a+b)}$ a + ${\textstyle \int a+\int b=\int (a+b)}$ $=$ ${\textstyle \int a+\int b=\int (a+b)}$ ( ${\textstyle \int a+\int b=\int (a+b)}$ a + ${\textstyle \int a+\int b=\int (a+b)}$ ) {{ $textstyle$ \ $int a$ +\ $int$ b $=\int ($ a + b ${\textstyle \int a+\int b=\int (a+b)}$ 를 사용하면 델타 변조기 앞에서 아날로그 신호를 재구성하는 적분기를 이동할 수 있습니다.
다시, 통합의 선형성 특성을 통해 두 적분기를 결합하고 델타 시그마 변조기/복조기 블록 다이어그램을 얻을 수 있습니다.

양자화가 균질한 경우(예: 선형인 경우) 위의 것은 가상의 등가성을 충분히 도출한 것입니다.그러나 양자화기가 균일하지 않기 때문에 델타 시그마는 델타 변조에서 영감을 얻지만 두 가지는 작동에서 구별됩니다.

그림 7의 첫 번째 블록 다이어그램에서, 피드백이 로우패스 필터의 입력으로부터 직접 획득되는 경우 피드백 경로의 적분기를 제거할 수 있습니다.따라서 입력 $신호 in$ v의 델타 변조의 경우 로우패스 필터가 신호를 확인합니다.

\"표시 스타일 \int \operatorname {Quantize} \left({\text{v}}_{\text{v}}-{\text{v}}_{\text{피드백}}_{\Delta }}\right)dt.\,}

그러나 동일한 입력 신호의 델타 시그마 변조가 로우패스 필터에 배치됩니다.

\"표시 스타일 \operatorname {Quantize} \left(\int \left({\text{v}}_{\text{v}}-{\text{v}}_{\Delta \Sigma }}\right)dt\right)\,},

즉, 델타 변조 대신 델타 시그마 변조를 수행하면 적분기 및 양자화기 작업의 순서가 효과적으로 바뀌었습니다.순 효과는 양자화 노이즈를 대부분 관심 신호보다 높은 주파수로 형성하는 심오한 추가 이점을 가진 더 간단한 구현입니다.이러한 효과는 오버샘플링이 증가함에 따라 더욱 극적으로 나타나 양자화 노이즈를 어느 정도 프로그래밍할 수 있습니다.반면에 델타 변조는 노이즈와 신호를 모두 동일하게 형성합니다.

또한 델타 변조에 사용되는 양자화기(예: 비교기)는 입력의 양자화된 근사치를 작은 단계로 표시하는 출력을 가지고 있지만 델타 시그마에 사용되는 양자화기는 입력 신호의 범위를 벗어나는 값을 취해야 합니다.

일반적으로 델타 시그마는 델타 변조에 비해 몇 가지 이점이 있습니다.

구조는 다음과 같이 단순화됩니다.
- 하나의 통합기만 필요합니다.
- 복조기는 신호를 재구성하기 위한 간단한 선형 필터(예: RC 또는 LC 필터)일 수 있습니다.
- 양자화기(예: 비교기)는 풀 스케일 출력을 가질 수 있습니다.
양자화된 값은 차분 신호의 적분이며, 다음은
- 신호의 변화 속도에 덜 민감하게 만듭니다.
- 저주파 및 DC 구성 요소를 캡처하는 데 도움이 됩니다.

아날로그-디지털 변환 예제

그림 8a: 간단한 델타 시그마 변환기의 개략도

그림 8b: 시간 경과에 따른 주요 전압 신호의 스코프 화면각 작은 수직 눈금은 1μs이며, 이는 1MHz 클럭의 샘플링 이벤트에 해당합니다.

델타 시그마 ADC는 복잡도가 다양합니다.아래 회로는 소멸이 없는 간단한 1차 2단계 양자화 델타 시그마 ADC에 초점을 맞춥니다.

단순화 회로 예제

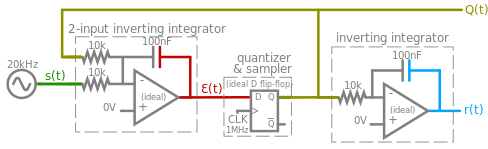
이해하기 쉽게 하기 위해 이상적인 요소를 사용하는 간단한 회로 다이어그램(그림 8a)을 시뮬레이션합니다(그림 8b 전압).이것은 그림 1의 아날로그-디지털 Δ 변조 루프와 동일한 기능입니다(참고: 2입력 반전 통합기는 합산 접합과 적분기를 결합하여 음의 피드백 결과를 생성하며, 플립 플랍은 샘플링된 양자화기를 결합하여 편리하게 1비트 DAC로도 기능합니다).

20kHz 입력 사인파(t)는 1비트 PDM 디지털 결과 Q(t)로 변환됩니다. 20kHz는 인간 청각의 상한으로 간주되기 때문에 예로 사용됩니다.

이 회로는 저렴한 개별 구성 요소로 빵판에 배치할 수 있습니다(일부 변형에서는 서로 다른 바이어스를 사용하고,^[22]^[23] 램프 대신 더 간단한 RC 로우패스 필터를 사용합니다).

간단히 말해, D 플립플랍은 V = +1 V 및_SS V = -1 V의 이중_DD 공급 전압으로 구동되므로, 이진 출력 Q(t)는 +1 V 또는 -1 V입니다.

2입력 반전 통합기

2입력 반전 앰프 통합기는 s(t)와 Q(t)를 결합하여 Δ(t)를 생성합니다.

\varepsilon (t)=-{\frac {1}{RC}}\int (s(t)+Q(t)dt.

그리스 문자 엡실론은 Δ(t)에 피드백 메커니즘에 의해 반복적으로 수정되는 누적 오류가 포함되어 있기 때문에 사용됩니다.입력 s(t)와 Q(t)가 모두 -1~1V 사이에서 변화하는 반면, Δ(t)는 약 0V에서 몇 밀리볼트만 변화합니다.

적분기의 음의 부호 때문에, Q(t)를 생성하기 위해 Δ(t) 다음을 샘플링할 때, 이 적분의 +Q(t)는 실제로 이전 클럭 사이클의 음의 피드백을 나타냅니다.

양자화기 및 샘플러 플립플랍

이상적인 D 플립플랍은 1MHz의 클럭 속도로 Δ(t)를 샘플링합니다.스코프 보기(그림 6b)는 1μs의 샘플링 주기와 동일한 작은 분할을 가지고 있으므로, 모든 작은 분할은 샘플링 이벤트에 해당합니다.플립플롭은 이상적인 것으로 간주되기 때문에 입력 전압이 0V에 아무리 가깝더라도 0V보다 큰 경우에는 논리적 높음으로, 0V보다 작은 경우에는 논리적 낮음으로 처리합니다(샘플 및 홀드 시간 위반 및 전이성 문제 무시).

샘플링 이벤트가 발생할 때마다:

Δ(t)가 0V 임계값을 초과하면 Q(t)가 하이(+1V)로 이동하거나,
Δ(t)가 0V 임계값 미만이면 Q(t)가 로우(-1V)가 됩니다.

Q(t)는 결과 PDM 출력으로 전송되고 2입력 반전 통합기로 피드백됩니다.

복조

가장 오른쪽에 있는 적분기는 Q(t)에서 디지털-아날로그 변환을 수행하여 원래 사인파 입력을 조각별 선형 대각 세그먼트로 재구성하는 복조 아날로그 출력 r(t)을 생성합니다.이 50배 초과 샘플링 속도에서 r(t)이 거칠어 보이지만, 원래 신호를 격리하기 위해 r(t)을 로우패스 필터링할 수 있습니다.샘플링 속도가 입력 신호의 최대 주파수에 비해 증가하면 r(t)이 원래 입력 s(t)에 더 가깝게 됩니다.

디지털-아날로그 변환

소멸이 발생하지 않은 경우 1비트 델타 시그마 변조기의 디지털 표현은 PDM 신호에 불과하며 저항기와 캐패시터처럼 ^[23]간단한 로우패스 필터를 사용하여 쉽게 아날로그로 변환할 수 있습니다.

그러나 일반적으로 델타 시그마 DAC는 높은 비트 깊이에서 디지털 샘플의 이산 시계열 신호를 낮은 비트 깊이(종종 1비트) 신호로 변환하며, 일반적으로 훨씬 높은 샘플링 속도로 변환합니다.그런 다음 델타 변조 신호를 아날로그로 정확하게 변환할 수 있습니다(비트 깊이가 낮은 DAC는 고선형화하기 쉬우므로). 그런 다음 델타 시그마 변조 프로세스에 고유한 고주파 양자화 노이즈를 제거하기 위해 아날로그 도메인에서 저렴한 저역 통과 필터링을 거칩니다.

업샘플링

이산 푸리에 변환 및 이산 시간 푸리에 변환 기사가 설명하듯이, 주기적으로 샘플링된 신호는 본질적으로 신호의 여러 더 높은 주파수 복사본 또는 "이미지"를 포함합니다.실제 델타 시그마 변조 단계를 수행하기 전에 이러한 고주파 이미지를 제거하여 최종 아날로그 로우패스 필터에 대한 요구 사항을 완화하는 것이 종종 바람직합니다.이는 보간 필터를 사용하여 업샘플링을 통해 수행할 수 있으며 DAC에서 델타 시그마 변조를 수행하기 전의 첫 번째 단계입니다.업샘플링은 델타 시그마 DAC와 강력하게 연관되어 있지만 실제 델타 시그마 변조 단계의 일부는 아닙니다(델타 시그마 ADC와 소멸이 강하게 연관되어 있는 방식과 유사하지만 델타 시그마 변조의 일부도 아닙니다). 자세한 내용은 이 기사의 범위에서 벗어납니다.

디지털-디지털 델타-시그마 변조

§ 노이즈 쉐이핑의 그림 6에 있는 변조 루프는 차이에 대한 감산기의 기본 디지털 요소, 적분기에 대한 축약기 및 양자화에 대한 하위 비트 레지스터를 사용하여 쉽게 배치될 수 있으며, 이는 다음 사이클에 대한 피드백이 될 적분기로부터 가장 중요한 비트를 전달합니다.

다단계 노이즈 쉐이핑

이 간단한 1차^st 변조는 각각 1차^st 델타 시그마 변조기와 동일한 두 개 이상의 오버플로우 어큐뮬레이터를 계단식으로 연결하여 개선할 수 있습니다.결과적으로 발생하는 다단계 노이즈 쉐이핑(MASH)^[24] 구조는 더 가파른 노이즈 쉐이핑 특성을 가지고 있으므로 디지털 오디오에서 일반적으로 사용됩니다.캐리 출력은 합산과 지연을 통해 결합되어 2진수 출력을 생성합니다. 이 출력의 폭은 MASH의 스테이지(순서) 수에 따라 달라집니다. 노이즈 쉐이핑 기능 외에도 다음과 같은 두 가지 매력적인 특성이 있습니다.

하드웨어에 구현하기 간단하며, 축전지, 가산기 및 D 플립플롭과 같은 공통 디지털 블록만 필요합니다.
무조건 안정적(축적기 외부에는 피드백 루프가 없음)

명명

이 기술은 1960년대 초 야스히코 교수가 ^[25]^[8]도쿄 대학 학생이었을 때 처음으로 제시했습니다.델타 시그마라는 이름은 이노세 등이 특허^{[clarification needed]} ^[6]출원에서 처음 도입한 것처럼 델타 변조기와 통합기의 존재에서 직접 유래했습니다.즉, 이 이름은 수학에서 일반적으로 각각 그리스 문자 시그마와 델타와 관련된 연산인 차이를 통합하거나 합산하여 얻은 것입니다.

1970년대에 벨 연구소 엔지니어들은 델타 변조에 대한 변형을 델타 앞에 형용사로 명명하는 선례가 있었기 때문에 "sigma-delta"라는 용어를 사용했고, 1990년 아날로그 장치 잡지 편집자는 함수 계층이 ^[26]차이의 적분을 계산하기 때문에 "sigma-delta"라고 정당화했습니다.

시그마-델타와 델타-시그마는 둘 다 자주 사용됩니다.

참고 항목

펄스 폭 변조
연속 가변 기울기 델타 변조
클래스 D 증폭기(때로는^[9] 델타 시그마 변조 사용)

메모들

^ 1962년 Inose 등이 설명한 델타 시그마 구성은 아날로그 신호의 정확한 전송 문제를 해결하기 위해 고안되었습니다.이 애플리케이션에서 전송된 것은 펄스 스트림이며 수신된 펄스가 재구성된 후 로우패스 필터로 원래 아날로그 신호가 복구되었습니다.이 로우패스 필터는 Δ와 관련된 합산 기능을 수행했습니다.전송 오류에 대한 고도의 수학적 처리는 그들에 의해 도입되었으며 펄스 스트림에 적용될 때 적절하지만 이러한 오류는 Δ와 관련된 축적 과정에서 손실됩니다.

레퍼런스

^ Sangil Park, Principles of Sigma-Delta Modulation for Analog-to-Digital Converters (PDF), Motorola, retrieved 2017-09-01
^ Inose, H.; Yasuda, Y. (1963-11-01). "A unity bit coding method by negative feedback". Proceedings of the IEEE. 51 (11): 1524–1535. doi:10.1109/PROC.1963.2622. ISSN 1558-2256 – via IEEE Xplore.
^ ^a ^b Wooley, Bruce A. (2012-03-22). "The Evolution of Oversampling Analog-to-Digital Converters" (PDF). IEEE. Archived (PDF) from the original on 2023-06-28. Retrieved 2023-06-28.
^ F. de Jager, "Delta 변조, 1단위 코드를 사용한 PCM 전송 방법", Philips Res. Rep., vol. 7, pp. 442–466, 1952.
^ 미국 특허 2967962, Cutler, Cassius C., "양자화를 이용한 전송 시스템", 1960년 3월 8일 발행.
^ ^a ^b Inose, H.; Yasuda, Y.; Murakami, J. (1962-05-06). "A Telemetering System by Code Modulation - Δ- ΣModulation". IRE Transactions on Space Electronics and Telemetry (published 1962-09-01). SET-8 (3): 204–209. doi:10.1109/IRET-SET.1962.5008839. ISSN 2331-1657. S2CID 51647729 – via IEEE Xplore.
^ Continuous-Time Sigma-Delta Modulation for A/D Conversion in Radio Receivers: Chapter 4: Continuous-time sigma-delta modulation. Springer Publishing. 2001. p. 29. doi:10.1007/0-306-48004-2_3. ISBN 9780306480041. Archived from the original on 2023-06-29. Retrieved 2023-06-28.
^ ^a ^b ^c ^d ^e Sangil Park, Principles of sigma-delta modulation for analog-to-digital converters (PDF), Motorola, archived from the original (PDF) on 2006-06-21
^ ^a ^b Jwin-Yen Guo 및 Teng-Hung Chang에 의한 시그마 델타 클래스 D 증폭기의 시그마 델타 클래스 D 증폭기 및 제어 방법
^ Lipschitz, Stanley P.; Vanderkooy, John (2000-09-22). "Why Professional 1-Bit Sigma-Delta Conversion is a Bad Idea" (PDF). Archived from the original (PDF) on 2022-11-02.
^ Lipshitz, Stanley P.; Vanderkooy, John (2001-05-12). "Why 1-Bit Sigma-Delta Conversion is Unsuitable for High-Quality Applications" (PDF). Archived (PDF) from the original on 2023-04-30. Retrieved 2023-08-28.
^ "Data Converter Architectures: Chapter 3" (PDF). Retrieved October 27, 2018.
^ "AN4990: Getting started with sigma-delta digital interface on applicable STM32 microcontrollers" (PDF). STMicroelectronics. March 2018. Archived (PDF) from the original on 2022-01-20. Retrieved 2023-09-03.
^ Kite, Thomas (2012). "Understanding PDM Digital Audio" (PDF). Archived (PDF) from the original on 2023-06-30. Retrieved 2023-08-24.
^ "MSP430i2xx Family" (PDF). Texas Instruments. 2014. Archived (PDF) from the original on 2022-10-15. Retrieved 2023-09-03.
^ Candy, J. (1974). "A Use of Limit Cycle Oscillations to Obtain Robust Analog-to-Digital Converters". IEEE Transactions on Communications. 22 (3): 298–305. doi:10.1109/TCOM.1974.1092194. ISSN 1558-0857.
^ S사의 다채널 대용량 롱 드리프트 액체 아르곤 TPC에서의 DAQ를 위한 새로운 아키텍처센트로, G. 멍, F.피에트로파올라, S. 벤추라 2006
^ Lombardi, A.; Bonizzoni, E.; Malcovati, P.; Maloberti, F. (2007). "A Low Power Sinc³ Filter for ΣΔ Modulators". 2007 IEEE International Symposium on Circuits and Systems. pp. 4008–4011. doi:10.1109/ISCAS.2007.378797. ISBN 978-1-4244-0920-4. S2CID 18354732.
^ ^a ^b ^c Van Ess, Dave. "Signals From Noise: Calculating Delta-Sigma SNRs" (PDF). Archived (PDF) from the original on 2023-08-06. Retrieved 2023-08-22.
^ Reiss, Joshua D. (2008). "UNDERSTANDING SIGMA–DELTA MODULATION: The Solved and Unsolved Issues" (PDF). J. Audio Eng. Soc., Vol. 56, No. 1/2, 2008 January/February. Archived (PDF) from the original on 2023-09-01. Retrieved 2023-09-01.
^ Brown, Ryan; Singh, Sameer (2016). "Application Report: General Oversampling of MSP ADCs for Higher Resolution" (PDF). Texas Instruments. Archived (PDF) from the original on 2022-09-01. Retrieved 2023-09-01.
^ "Activity: Delta - Sigma Modulator [Analog Devices Wiki]". Analog Devices. 2021-01-09. Archived from the original on 2023-04-01. Retrieved 2023-07-01.
^ ^a ^b Ellsworth, Jeri (2012-11-05). "One Bit ADC - Short Circuits". YouTube. Retrieved 2023-06-29.{{cite web}}CS1 유지보수: url-status(링크)
^ "15-25 MHZ Fractional-N Synthesizer".
^ "発見と発明のデジタル博物館卓越研究データベース・電気・情報通信関連・研究情報（登録番号671)". Archived from the original on 2022-04-08.
^ Sheingold, Dan (1990). "Editor's Notes: Σ-∆ or ∆-Σ?" (PDF). Analog Devices. Archived (PDF) from the original on 2023-06-29. Retrieved 2023-06-28.

진일보한 내용

Walt Kester (October 2008). "ADC Architectures III: Sigma-Delta ADC Basics" (PDF). Analog Devices. Retrieved 2010-11-02.
R. Jacob Baker (2009). CMOS Mixed-Signal Circuit Design (2nd ed.). Wiley-IEEE. ISBN 978-0-470-29026-2.
R. Schreier; G. Temes (2005). Understanding Delta-Sigma Data Converters. Wiley. ISBN 978-0-471-46585-0.
S. Norsworthy; R. Schreier; G. Temes (1997). Delta-Sigma Data Converters. Wiley. ISBN 978-0-7803-1045-2.
J. Candy; G. Temes (1992). Oversampling Delta-sigma Data Converters. ISBN 978-0-87942-285-1.

외부 링크

1비트 A/D 및 D/A 변환기
Sigma-Delta 기술은 Tim Wescott의 DAC 해결 기사를 확장합니다. 2004-06-23.
Delta-Sigma Modulator 설계 튜토리얼: Mingliang(Michael) Liu의 Part I 및 Part II
가보르 테메스의 출판물
Sigma-Delta Modulation Primer Part II 블록 다이어그램, 코드 및 간단한 설명 포함
연속 시간 시그마 델타 ADC를 위한 시뮬레이션 링크 모델 및 스크립트 예제 matlab 코드 및 시뮬레이션 링크 모델 포함
브루스 울리의 델타 시그마 변환기 프로젝트
델타 시그마 변환기 소개(ADC와 DAC 시그마 델타 모두 포함)
Sigma-Delta ADC를 해독하는 중입니다.이 심층 기사는 델타 시그마 아날로그-디지털 변환기 뒤의 이론을 다룹니다.
원비트 델타 시그마 D/A 변환 파트 I: 2004 comp.dsp 컨퍼런스에서 발표된 랜디 예이츠의 이론 기사
MASH(Multi-Stage Noise Shaping) 구조와 MASH의 블록 레벨 구현
연속 시간 시그마 델타 ADC 노이즈 쉐이핑 필터 회로 아키텍처는 연속 시간 시그마 델타 노이즈 쉐이핑 필터에 대한 구조적 트레이드오프를 논의합니다.
델타 시그마 변환기: 변조 – 델타 시그마 변조기가 작동하는 이유에 대한 직관적인 동기 부여
시그마 델타 변조를 이용한 피드백 제어 기능이 있는 디지털 가속도계
아날로그 장치 Sigma-Delta ADC 튜토리얼(대화형)

[8] 1962년 Inose 등이 설명한 델타 시그마 구성은 아날로그 신호의 정확한 전송 문제를 해결하기 위해 고안되었습니다.이 애플리케이션에서 전송된 것은 펄스 스트림이며 수신된 펄스가 재구성된 후 로우패스 필터로 원래 아날로그 신호가 복구되었습니다.이 로우패스 필터는 Δ와 관련된 합산 기능을 수행했습니다.전송 오류에 대한 고도의 수학적 처리는 그들에 의해 도입되었으며 펄스 스트림에 적용될 때 적절하지만 이러한 오류는 Δ와 관련된 축적 과정에서 손실됩니다.

[1] Sangil Park, Principles of Sigma-Delta Modulation for Analog-to-Digital Converters (PDF), Motorola, retrieved 2017-09-01

[2] Inose, H.; Yasuda, Y. (1963-11-01). "A unity bit coding method by negative feedback". Proceedings of the IEEE. 51 (11): 1524–1535. doi:10.1109/PROC.1963.2622. ISSN 1558-2256 – via IEEE Xplore.

[:0-3] Wooley, Bruce A. (2012-03-22). "The Evolution of Oversampling Analog-to-Digital Converters" (PDF). IEEE. Archived (PDF) from the original on 2023-06-28. Retrieved 2023-06-28.

[4] F. de Jager, "Delta 변조, 1단위 코드를 사용한 PCM 전송 방법", Philips Res. Rep., vol. 7, pp. 442–466, 1952.

[5] 미국 특허 2967962, Cutler, Cassius C., "양자화를 이용한 전송 시스템", 1960년 3월 8일 발행.

[Inose-6] Inose, H.; Yasuda, Y.; Murakami, J. (1962-05-06). "A Telemetering System by Code Modulation - Δ- ΣModulation". IRE Transactions on Space Electronics and Telemetry (published 1962-09-01). SET-8 (3): 204–209. doi:10.1109/IRET-SET.1962.5008839. ISSN 2331-1657. S2CID 51647729 – via IEEE Xplore.

[7] Continuous-Time Sigma-Delta Modulation for A/D Conversion in Radio Receivers: Chapter 4: Continuous-time sigma-delta modulation. Springer Publishing. 2001. p. 29. doi:10.1007/0-306-48004-2_3. ISBN 9780306480041. Archived from the original on 2023-06-29. Retrieved 2023-06-28.

[:3-9] Sangil Park, Principles of sigma-delta modulation for analog-to-digital converters (PDF), Motorola, archived from the original (PDF) on 2006-06-21

[:2-10] Jwin-Yen Guo 및 Teng-Hung Chang에 의한 시그마 델타 클래스 D 증폭기의 시그마 델타 클래스 D 증폭기 및 제어 방법

[11] Lipschitz, Stanley P.; Vanderkooy, John (2000-09-22). "Why Professional 1-Bit Sigma-Delta Conversion is a Bad Idea" (PDF). Archived from the original (PDF) on 2022-11-02.

[12] Lipshitz, Stanley P.; Vanderkooy, John (2001-05-12). "Why 1-Bit Sigma-Delta Conversion is Unsuitable for High-Quality Applications" (PDF). Archived (PDF) from the original on 2023-04-30. Retrieved 2023-08-28.

[analog-13] "Data Converter Architectures: Chapter 3" (PDF). Retrieved October 27, 2018.

[14] "AN4990: Getting started with sigma-delta digital interface on applicable STM32 microcontrollers" (PDF). STMicroelectronics. March 2018. Archived (PDF) from the original on 2022-01-20. Retrieved 2023-09-03.

[15] Kite, Thomas (2012). "Understanding PDM Digital Audio" (PDF). Archived (PDF) from the original on 2023-06-30. Retrieved 2023-08-24.

[16] "MSP430i2xx Family" (PDF). Texas Instruments. 2014. Archived (PDF) from the original on 2022-10-15. Retrieved 2023-09-03.

[17] Candy, J. (1974). "A Use of Limit Cycle Oscillations to Obtain Robust Analog-to-Digital Converters". IEEE Transactions on Communications. 22 (3): 298–305. doi:10.1109/TCOM.1974.1092194. ISSN 1558-0857.

[18] S사의 다채널 대용량 롱 드리프트 액체 아르곤 TPC에서의 DAQ를 위한 새로운 아키텍처센트로, G. 멍, F.피에트로파올라, S. 벤추라 2006

[19] Lombardi, A.; Bonizzoni, E.; Malcovati, P.; Maloberti, F. (2007). "A Low Power Sinc³ Filter for ΣΔ Modulators". 2007 IEEE International Symposium on Circuits and Systems. pp. 4008–4011. doi:10.1109/ISCAS.2007.378797. ISBN 978-1-4244-0920-4. S2CID 18354732.

[:4-20] Van Ess, Dave. "Signals From Noise: Calculating Delta-Sigma SNRs" (PDF). Archived (PDF) from the original on 2023-08-06. Retrieved 2023-08-22.

[21] Reiss, Joshua D. (2008). "UNDERSTANDING SIGMA–DELTA MODULATION: The Solved and Unsolved Issues" (PDF). J. Audio Eng. Soc., Vol. 56, No. 1/2, 2008 January/February. Archived (PDF) from the original on 2023-09-01. Retrieved 2023-09-01.

[22] Brown, Ryan; Singh, Sameer (2016). "Application Report: General Oversampling of MSP ADCs for Higher Resolution" (PDF). Texas Instruments. Archived (PDF) from the original on 2022-09-01. Retrieved 2023-09-01.

[23] "Activity: Delta - Sigma Modulator [Analog Devices Wiki]". Analog Devices. 2021-01-09. Archived from the original on 2023-04-01. Retrieved 2023-07-01.

[:1-24] Ellsworth, Jeri (2012-11-05). "One Bit ADC - Short Circuits". YouTube. Retrieved 2023-06-29.{{cite web}}CS1 유지보수: url-status(링크)

[25] "15-25 MHZ Fractional-N Synthesizer".

[26] "発見と発明のデジタル博物館卓越研究データベース・電気・情報通信関連・研究情報（登録番号671)". Archived from the original on 2022-04-08.

[27] Sheingold, Dan (1990). "Editor's Notes: Σ-∆ or ∆-Σ?" (PDF). Analog Devices. Archived (PDF) from the original on 2023-06-29. Retrieved 2023-06-28.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[note 1]

[8]

[9]

[10]

[11]

[12]

[14]

[13]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

Search

델타 시그마 변조

네임스페이스

더

목차

동기

오버샘플링의 장점

주파수/해상도 트레이드오프

델타 변조 대비 개선

1비트 델타 변조는 펄스 밀도 변조입니다.

역사와 변주곡

고차 변조기

멀티비트 양자화기

후속 소멸

오버샘플링 비율 및 ΔM 순서를 높여 베이스밴드 노이즈 감소

양자화 노이즈 확산을 위한 오버샘플링

노이즈 셰이핑

라플라스 영역에서의 Δ ADC 변조 루프 해석

입력 시 로우패스 필터

하이패스 필터 온 노이즈

z-도메인에서의 Δ 변조 루프 해석

고차 변조기

이론적 유효 비트 수

델타 변조와의 관계

아날로그-디지털 변환 예제

단순화 회로 예제

2입력 반전 통합기

양자화기 및 샘플러 플립플랍

복조

디지털-아날로그 변환

업샘플링

디지털-디지털 델타-시그마 변조

다단계 노이즈 쉐이핑

명명

참고 항목

메모들

레퍼런스

진일보한 내용

외부 링크