생일문제

확률 이론에서 생일 문제는 임의로 선택된 n명의 사람들로 구성된 집합에서 적어도 두 명이 생일을 공유할 확률을 요구합니다.생일 역설이란 그 확률이 50%를 넘으려면 23명만 필요하다는 반직관적인 사실을 말합니다.

생일 역설은 처음에는 틀린 것처럼 보이지만 사실은 사실입니다.생일을 공유할 확률이 50%에 도달하는 데 23명만 필요한 것은 놀랄 수 있지만, 이 결과는 가능한 모든 사람들 간의 생일 비교가 이루어질 것이라는 점을 고려함으로써 더 직관적으로 만들어 졌습니다.23명의 사람들과 함께,23 × 22/2 = 253 쌍을 고려해야 하며, 이는 1년 중 일수의 절반을 훨씬 초과합니다.

생일 문제에 대한 실제 응용 프로그램에는 생일 공격이라는 암호 공격이 포함되어 있는데, 이는 해시 함수에 대한 충돌을 찾는 복잡성을 줄이기 위해 이 확률적 모델을 사용할 뿐만 아니라 주어진 인구 규모의 해시 내에 존재하는 해시 충돌의 대략적인 위험을 계산합니다.

이 문제는 일반적으로 1927년쯤에 해럴드 대븐포트가 그 당시에는 출판하지 않았지만, 그 때문이라고 추정됩니다.대븐포트는 "이전에 언급되지 않았다고 믿을 수 없었기 때문에" 발견자라고 주장하지 않았습니다.^[1][2]생일 문제의 첫번째 버전은 1939년에 Richard von Mises에 의해서 출판되었습니다.^[3]

확률 계산

순열의 관점에서, 사건 A를 반복되는 생일이 없는 23명의 그룹을 발견할 확률이라고 가정합니다.여기서 이벤트 B가 적어도 두 사람이 같은 생일을 공유하는 23명의 그룹을 발견할 확률인 P(B) = 1 - P(A)입니다. P(A$)$는 반복 및 순서 문제 없이 총 생일 수 Vnr {\$displaystyle V_{nr}$의 비율입니다(예: 2명의 그룹, mm/dd 생일 형식). ${\displaystyle \mathrm{하나}}$의 가능한 결과는 ${\displaystyle \{01}$ ${\displaystyle /}$ ${\displaystyle 02,}$ 0${\$$\right\}}$를 반복 및 순서 문제가 있는 생일의 총 개수로$$ ${\displaystyle {나눈}_{}}$ Vt$${\$displaystyle$V_${t$}, 실험 결과의 총 공간이므로$($예: 2명, 가능한 결과는${\displaystyle \{\{}$ ${\displaystyle 01}$/ ${\displaystyle 02,}$ ${\displaystyle 01}$/ ${\displaystyle 02}$ ${\displaystyle \},}${ ${\displaystyle 10}$/ ${\displaystyle 02,}$ ${\displaystyle 08}$/ ${\displaystyle 04}$ ${\displaystyle \},}$ ${\$$\right$따라서 ${\displaystyle {\mathrm{Vnr}}_{}}$ ${\$와 ${\displaystyle {Vt}_{}}$ ${\$가 순열입니다.

${\displaystyle {\begin{aligned}V_{nr}&={\frac {n!}{(n-k)!}}={\frac {365!}{(365-23)!}}\V_{t}&=n^{k}=365^{23}\P(A)&={\frac {V_{nr}{V_{t}}\근 0.492703\P(B)&=1-P(A)\근 1-0.492703\approx 0.507297(50.7297\%)\end{aligned}}$

생일 문제를 해결할 수 있는 또 다른 방법은 n명으로 이루어진 그룹에서 적어도 두 명의 생일이 같은 확률을 대략적으로 묻는 것입니다.단순화를 위해 윤년, 쌍둥이, 선택 편향, 출생률의^[4] 계절적, 주간적 변동은 일반적으로 무시되며 대신 365명의 가능한 생일이 있다고 가정하고, 각 사람의 생일은 그룹의 다른 사람들과 관계없이 동일하게 이 날 중 어느 날이 될 가능성이 있다고 가정합니다.독립적인 생일의 경우 생일에 대한 균일 분포는 생일이 같은 두 사람의 확률을 최소화하는 분포입니다. 불규칙성이 있으면 이 확률이 증가합니다.^[5][6]1년 중 매일 발생하는 출생의 수가 일정하지 않은 문제는 1967년 머레이 클램킨에 의해 처음으로 다루어졌다.^{[7][failed verification]}실제 분포에서 임계 크기는 23에서 50%^[8]에 이릅니다.

목표는 P(A)를 계산하는 것입니다. P(A)는 방에 있는 최소 두 사람의 생일이 같을 확률입니다.그러나 P(A')를 계산하는 것이 더 간단합니다. 즉, 방에 있는 두 사람의 생일이 같지 않을 확률입니다.그렇다면, A와 A'는 유일한 두 가지 가능성이며, 또한 상호 배타적이기 때문에, P(A) = 1 - P(A').

여기 23명에 대한 P(A) 계산이 있습니다.23명에게 1부터 23까지 번호를 매기게 해주세요.23명의 생일이 모두 다른 경우는 2명의 생일이 1명과 같지 않고, 3명의 생일이 1명과 2명 중 어느 한 명의 생일도 같지 않고, 마지막으로 23명의 생일이 1명부터 22명 중 어느 한 명과 같지 않은 경우와 같습니다.이러한 이벤트를 이벤트 2, 이벤트 3 등이라고 합니다.이벤트 1은 확률 1로 발생하는 생일 이벤트입니다.이 이벤트의 연결은 조건부 확률을 사용하여 계산될 수 있습니다. 이벤트 2의 확률은 364/365입니다. 사람 2는 사람 1의 생일 외에 다른 생일을 가질 수 있기 때문입니다.마찬가지로, 이벤트 2가 발생했을 때 이벤트 3의 확률은 363/365이며, 이벤트 3은 1과 2가 아직 촬영하지 않은 생일 중 하나를 가질 수 있기 때문입니다.이는 모든 이전 이벤트가 343/365임을 고려할 때 이벤트 23의 확률이 최종적으로 유지될 때까지 계속됩니다.마지막으로 조건부 확률의 원리는 P(A')가 다음과 같은 개별 확률의 곱과 같다는 것을 의미합니다.

${\displaystyle P(A')={\frac {365}{365}}\time {\frac {364}{365}}\time {\frac {362}{365}}\time \cdots \time {\frac {343}{365}}$

(1)

식 (1)의 조건을 수집하면 다음과 같은 값을 얻을 수 있습니다.

${\displaystyle P(A')=\left({\frac {1}{365}}\right)^{23}\times(365\times 364\times 363\times \cdots \times 343)}$

(2)

식 (2)를 평가하면 P(A') ≈이 0.492703이 됩니다.

따라서 P(A) ≈ 1 - 0.492703 = 0.507297 (50.7297%).

이 과정은 n명으로 이루어진 그룹으로 일반화될 수 있으며, 여기서 p(n)은 적어도 두 명의 사람들이 생일을 공유할 확률입니다.먼저 모든 n개의 생일이 다를 확률 p(n)을 계산하는 것이 더 쉽습니다.p(n)은 비둘기 구멍 원리에 따라 n > 365일 때 0입니다.n ≤ 365인 경우:

${\displaystyle {\begin{aligned}{\bar {p}}(n)&=1\times \left(1-{\frac {1}{365}}\right)\times \cdots \left(1-{\frac {2}{365}\right)\times \left(1-{\frac {n-1}{365}\right)\times \times \left(1-{\frac {n-1}{365})\right)\times \times \left(1-{\frac {1})\times\[6pt]&={\frac {365\times 364\times \cdots \times (365-n+1)}{365^{n}}\[6pt]&={\frac {365!} {365^{n}(365-n)!}}={\frac {n!\cdot {\binom {365}{n}}{365^{n}}={\frac {_{365}P_{n}}{365^{n}}}\end{aligned}}$

여기서!는 요인 연산자이고,³⁶⁵
_n ()는 이항 계수이고_r, P는 순열을 나타냅니다.

이 방정식은 첫 번째 사람은 생일을 공유할 사람이 없고, 두 번째 사람은 첫 번째 사람과 같은 생일을 가질 수 없으며(364/365), 세 번째 사람은 첫 번째 두 사람 중 하나와 같은 생일을 가질 수 없으며(363/365), 일반적으로 n번째 생일은 n - 1 이전 생일 중 하나와 같을 수 없다는 사실을 나타냅니다.

n명 중 최소 2명의 생일이 같은 경우는 모든 n명의 생일이 다른 것과 보완적입니다.따라서 확률 p(n)은

${\displaystyle p(n)=1-{\bar {p}}(n).}$

다음 표는 n의 다른 값에 대한 확률을 보여줍니다(이 표의 경우 윤년의 존재는 무시되며 각 생일은 동일한 가능성이 있는 것으로 가정됩니다).

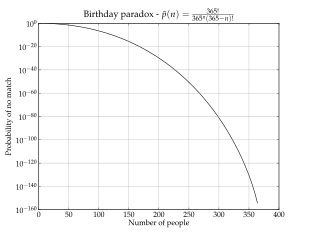
n	p(n)
1	00.0%
5	02.7%
10	11.7%
20	41.1%
23	50.7%
30	70.6%
40	89.1%
50	97.0%
60	99.4%
70	99.9%
75	99.97%
100	99.99997%
200	99.9999999999999999999999999998%
300	(100 - 6x10−80)%
350	(100 - 3x10−129)%
365	(100 - 1.45x10−155)%
≥ 366	100%

근사치

지수 함수의 테일러 급수 확장(상수 e ≈ 2.718281828)

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots }$

${\displaystyle x}$ ≪ ${\displaystyle 1}$ ${\displaystyle$x \$ll 1}$에 대한 e의 1차 근사치를 제공합니다$.$

${\displaystyle e^{x}\approx 1+x.}$

p(n)에 대해 도출된 첫 번째 식에 이 근사치를 적용하려면 x = -a/365를 설정합니다.따라서,

${\displaystyle e^{-{\frac {a}{365}}\approx 1-{\frac {a}{365}}.$

그런 다음 a = n - 1이 될 때까지 p(n) 공식의 각 항에 대해 a를 음이 아닌 정수로 대체합니다. 예를 들어 a = 1일 때,

${\displaystyle e^{-{\frac {1}{365}}\approx 1-{\frac {1}{365}}}$

p(n)에 대해 도출된 첫 번째 식을 다음과 같이 근사화할 수 있습니다.

${\displaystyle {\begin{aligned}{\bar {p}}(n)&\cdot e^{-{\frac {1}{365}}\cdot e^{-{\frac {2}{365}}\cdot e^{-{\frac {n-1}{365}}\[6pt]&=e^{-{\frac {1+2+\,\cdots \,+(n-1)}{365}}\[6pt]&=e^{-{\frac {n(n-1)/2}{365}=e^{-{\frac {n(n-1)}{730}}.\end{aligned}}$

그러므로,

${\displaystyle p(n)=1-{\bar {p}}(n)\approx 1-e^{-{\frac {n(n-1)}{730}}}}$

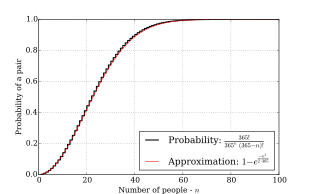
더 대략적인 근사치는 다음과 같습니다.

${\displaystyle p(n)\approx 1-e^{-{\frac {n^{2}}{730}},}$

그래프가 보여주듯이, 여전히 꽤 정확합니다.

근사치에 따르면, 동일한 접근 방식이 "사람"과 "날"의 수에 상관없이 적용될 수 있습니다.365일이 아니라 d이고, n명이 있고, n명이 ≪일 경우 위와 같은 접근법을 사용하면 p(n, d)가 d일의 집합으로부터 n명 중 적어도 2명이 같은 생일을 공유할 확률이 된다는 결과를 얻을 수 있습니다.

${\displaystyle {\begin{aligned}p(n,d)&\approx 1-e^{-{\frac {n(n-1)}{2d}}\[6pt]&\approx 1-e^{-{\frac {n^{2}}{2d}}}.\end{aligned}}$

단순 지수화

어느 두 사람이라도 같은 생일이 아닐 확률은 364/365입니다.n명이 있는 방에는 () = n(n - 1)/2쌍의 사람, 즉 () 이벤트가 있습니다.같은 생일을 함께 보내는 두 사람이 없을 확률은 이 사건들이 독립적이라고 가정하고 그들의 확률을 곱함으로써 근사화될 수 있습니다.독립적인 것은 방에만 있는 것이 아니라, 세상의 어떤 한 쌍의 사람이라도 대신에 선택하는 것과 같습니다.간단히 말해서 364/365는 그 자체로 ()ⁿ
₂ 곱해질 수 있고, 이것은 우리에게 다음을 줍니다.

${\displaystyle {\bar {p}}(n)\approx \left ({\frac {364}{365}\right)^{\binom {n}{2}}}$

이것은 같은 생일을 가진 사람이 없을 확률이기 때문에, 누군가가 생일을 공유할 확률은

${\displaystyle p(n)\approx 1-\left ({\frac {364}{365}}\right)^{\binom {n}{2}}}$

그리고 23명으로 이루어진 그룹의 경우, 공유할 확률은

${\displaystyle p(23)\approx 1-\left ({\frac {364}{365}}\right)^{\binom {23}{2}}=1-\left ({\frac {364}{365}\right)^{253}\approx 0.500477.}$

포아송 근사치

23명으로 구성된 그룹에서 이항에 대한 포아송 근사치를 적용하면,

${\displaystyle \operatorname {Poi} \left ({\frac {\binom {23}{2}}{365}\right)=\operatorname {Poi} \left ({\frac {253}{365}\right)\approx \operatorname {Poi} (0.6932)}$

그렇게

${\displaystyle \Pr(X>0)=1-\Pr(X=0)\약 1-e^{-0.6932}\approx 1-0.49998=0.500002.}$

결과는 앞에서 설명한 것과 같이 50% 이상입니다.이 근사치는 e ≈ 1 + x를 사용하는 Taylor 확장을 기반으로 한 위의 근사치와 동일합니다.

제곱근사

정신적 계산에 사용될 수 있는 좋은 경험의 법칙은 관계입니다.

${\displaystyle p(n)\approx {\frac {n^{2}}{2m}}$

다음과 같이 적을 수도 있습니다.

${\displaystyle n\approx {\sqrt {2m\times p(n)}}$

1/2 이하의 확률에 적합한 값입니다.이들 방정식에서 m은 1년 동안의 일수입니다.

예를 들어, 공유 생일의 1/2 확률에 필요한 사람들의 수를 추정하기 위해, 우리는

${\displaystyle n\approx {\sqrt {2\times 365\times {\tfrac {1}{2}}}}={\sqrt {365}\approx 19}$

그것은 23의 정답에서 그리 멀지 않은 것입니다.

인원추계

이는 또한 최소 1/2의 일치 가능성을 갖는 데 필요한 사람의 수에 대해 다음 공식을 사용하여 근사화할 수 있습니다.

${\displaystyle n\geq {\tfrac {1}{2}}+{\sqrt {\tfrac {1}{4}}+2\times \ln(2)\times 365}}=22.99943.}$

이는 knn을 2번 반복할 경우 1/k 확률의 사건이 적어도 1회 발생할 확률이 1/2이라는 좋은 근사치의 결과입니다.^[9]

확률표

의 길이 육각 끈	의 조각조각 (b)	해시 공간 크기 (2b)	적어도 하나의 해시 충돌 확률이 ≥ p인 해시 요소의 수
			p = 10	p = 10	p = 10	p = 10	p = 10	p = 0.001	p = 0.01	p = 0.25	p = 0.50	p = 0.75
8	32	4.3x109	2	2	2	2.9	93	2.9x103	9.3x103	5.0x104	7.7x104	1.1x105
(10)	(40)	(1.1x1012)	2	2	2	47	1.5x103	4.7x104	1.5x105	8.0x105	1.2x106	1.7x106
(12)	(48)	(2.8x1014)	2	2	24	7.5x102	2.4x104	7.5x105	2.4x106	1.3x107	2.0x107	2.8x107
16	64	1.8x1019	6.1	1.9x102	6.1x103	1.9x105	6.1x106	1.9x108	6.1x108	3.3x109	5.1x109	7.2x109
(24)	(96)	(7.9x1028)	4.0x105	1.3x107	4.0x108	1.3x1010	4.0x1011	1.3x1013	4.0x1013	2.1x1014	3.3x1014	4.7x1014
32	128	3.4x1038	2.6x1010	8.2x1011	2.6x1013	8.2x1014	2.6x1016	8.3x1017	2.6x1018	1.4x1019	2.2x1019	3.1x1019
(48)	(192)	(6.3x1057)	1.1x1020	3.5x1021	1.1x1023	3.5x1024	1.1x1026	3.5x1027	1.1x1028	6.0x1028	9.3x1028	1.3x1029
64	256	1.2x1077	4.8x1029	1.5x1031	4.8x1032	1.5x1034	4.8x1035	1.5x1037	4.8x1037	2.6x1038	4.0x1038	5.7x1038
(96)	(384)	(3.9x10115)	8.9x1048	2.8x1050	8.9x1051	2.8x1053	8.9x1054	2.8x1056	8.9x1056	4.8x1057	7.4x1057	1.0x1058
128	512	1.3x10154	1.6x1068	5.2x1069	1.6x1071	5.2x1072	1.6x1074	5.2x1075	1.6x1076	8.8x1076	1.4x1077	1.9x1077

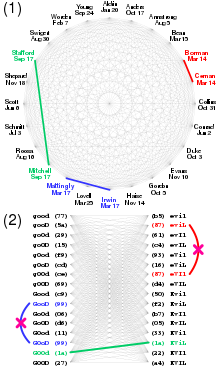
이 표의 밝은 필드는 특정 크기의 해시 공간(행)이 주어지면 주어진 충돌 확률(열)을 달성하는 데 필요한 해시 수를 비트(행)로 표시합니다.생일 비유를 사용하면, "해시 공간 크기"는 "사용 가능한 날짜"와 유사하고, "충돌 가능성"은 "공유 생일의 확률"과 유사하며, "필요한 해시 요소 수"는 "그룹의 필요한 인원 수"와 유사합니다.또한 이 차트를 사용하여 필요한 최소 해시 크기(해시와 오류 가능성에 상한이 주어짐) 또는 충돌 가능성(해시의 고정 수와 오류 가능성)을 확인할 수 있습니다.

비교를 위해 10에서⁻¹⁸ 10은⁻¹⁵ 일반적인 하드 디스크의 정정 불가능한 비트 오류율입니다.^[10]이론적으로 MD5와 같은 128비트 해시 함수는 가능한 출력이 더 많더라도 약 8.2×10¹¹ 문서가 나올 때까지 그 범위 내에 있어야 합니다.

확률의 상한과 인원의 하한

아래의 주장은 Paul Halmos의 주장을 각색한 것입니다.^{[nb 1]}

위와 같이 두 생일이 일치하지 않을 확률은

${\displaystyle 1-p(n)={\bar {p}}(n)=\prod_{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).}$

이전 단락에서와 같이 관심은 p(n) > 1/2인 가장 작은 n에 있습니다. 또는 동등하게 p(n) < 1/2인 가장 작은 n에 있습니다.

위 식에서 부등식 1 - x < e를^−x 사용하여 1 - k/365를 e로^−k⁄365 대체합니다.이것은 산출합니다.

${\displaystyle {\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right)<\prod _{k=1}^{n-1}\left(e^{-{\frac {k}{365}}\right)=e^{-{\frac {n(n-1)}{730}}}.$

따라서 위 식은 근사일 뿐만 아니라 p(n)의 상한이기도 합니다.부등식

${\displaystyle e^{-{\frac {n(n-1)}{730}}<{\frac {1}{2}}}$

p(n) < 1/2을 암시합니다.n개의 선물을 해결하는 것

${\displaystyle n^{2}-n>730\ln 2.}$

이제 730 ln 2는 약 505.997로, n = 23일 때 n - n의 값인 506보다 약간 낮습니다.따라서 23명이면 충분합니다.덧붙여서 n - n = 730 ln 2를 n으로 풀면 위에서 인용한 Frank H. Math의 근사식이 나옵니다.

이 유도는 생일이 짝수로 일치하도록 하려면 최대 23명의 사람이 필요하다는 것을 보여줄 뿐입니다. n이 22이거나 그 이하일 수 있는 가능성을 열어 둡니다.

일반화

임의일수

d일이 있는 해가 주어지면, 일반화된 생일 문제는 무작위로 선택된 n명의 사람들의 집합에서 생일 일치 확률이 최소 50%가 되도록 최소 n(d)을 요구합니다.즉, n(d)는 다음과 같은 최소 정수 n이다.

${\displaystyle 1-\left(1-{\frac {1}{d}}\right)\left(1-{\frac {2}{d}}\right)\cdots\left(1-{\frac {n-1}{d}\right)\geq {\frac {1}{2}}}$

따라서 고전적 생일 문제는 n(365)을 결정하는 것에 해당합니다.n(d)의 첫 99개의 값이 여기에 주어집니다(OEIS의 시퀀스 A033810).

d	1–2	3–5	6–9	10–16	17–23	24–32	33–42	43–54	55–68	69–82	83–99
n(d)	2	3	4	5	6	7	8	9	10	11	12

비슷한 계산에 따르면 d가 341-372 범위에 있을 때 n(d) = 23이 됩니다.

n(d)에 대한 많은 경계와 공식이 발표되었습니다.^[11]임의의 d ≥ 1에 대하여, n(d)는 다음을 만족합니다.

${\displaystyle {\frac {3-2\ln 2}{6}}<n(d)-{\sqrt {2d\ln 2}}\leq 9-{\sqrt {86\ln 2}}$

이러한 경계는 n(d) - √2d ln 2 수열이 임의로 가까워진다는 점에서 최적입니다.

${\displaystyle {\frac {3-2\ln2}{6}}\approx 0.27,}$

있는 동안에

${\displaystyle 9-{\sqrt {86\ln2}}\approx 1.28}$

최대치로서 d = 43에 대해 취합니다.

대부분의 경우 n(d)의 정확한 값을 제공할 수 있을 정도로 경계가 좁습니다.예를 들어, d = 365의 경우 이러한 경계는 22.7633 < n(365) < 23.7736 및 23이 해당 범위의 유일한 정수임을 나타냅니다.일반적으로 n(d)는 항상 다음 중 하나와 같음을 알 수 있습니다.

${\displaystyle \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil \quad {\text{or}}\left\lceil {\sqrt {2d\ln 2}\,\right\rceil +1}$

여기서 ⌈ · ⌉은 천장 함수를 나타냅니다.공식을

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil }$

모든 정수 d의 73%를 차지합니다.^[13]공식을

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}\right\rceil }$

는 거의 모든 d, 즉 점근 밀도가 1인 정수 집합에 대해 성립합니다.^[13]

공식을

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}\right\rceil }$

는 모든 d ≤ 10¹⁸ 을 갖지만, 이 공식에는 무한히 많은 반례가 있을 것으로 추측됩니다.^[14]

공식을

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}}}-{\frac {2(\ln 2)^{2}}}-{\frac {2(\ln 2)^{135d}}\right\rceil }$

는 모든 d ≤ 10¹⁸ 을 가지며, 이 공식은 모든 d 를 가지는 것으로 추측됩니다.^[14]

두 명 이상의 사람들이 생일을 공유하는 경우

그룹의 최소 3명, 4명, 5명 등이 같은 생일을 공유할 확률이 50% 이상이 되려면 그룹에 몇 명이 필요한지 묻는 문제를 확장할 수 있습니다.

처음 몇 개의 값은 다음과 같습니다. >3명이 생일을 공유할 확률 50% - 88명; >4명이 생일을 공유할 확률 50% - 187명 (OEIS의 시퀀스 A014088).^[15]

생일 공유 확률(충돌)

생일 문제는 다음과 같이 일반화할 수 있습니다.

범위가 [1,d]인 이산 균일 분포에서 추출된 n개의 임의 정수가 주어졌을 때, 최소 두 개의 숫자가 동일할 확률은 p(n;d)는 얼마입니까?(d = 365는 일반적인 생일 문제를 제공합니다.)

일반적인 결과는 위에 제시된 것과 같은 인수를 사용하여 도출할 수 있습니다.

${\displaystyle {\begin{aligned}p(n;d)&={\begin{case}1-\displaystyle \prod _{k=1}^{n-1}\left(1-{\frac {k}{d}\right)&n\leq d\1&n>d\end{case}}\\[8px]&\e^{-{\frac {n(n-1)}{2d}}\&\approx 1-\left ({\frac {d-1}{d}\right)^{\frac {n(n-1)}{2}}\end{aligned}}$

반대로, n(p; d)가 [1,d]로부터 추출된 임의의 정수의 수를 나타내면, 적어도 두 개의 숫자가 동일할 확률 p를 얻을 수 있습니다.

${\displaystyle n(p;d)\approx {\sqrt {2d\cdot \ln \left ({\frac {1}{1-p}}\right)}}}.$

보다 일반적인 의미에서 생일 문제는 해시 함수에 적용됩니다. 충돌하기 전에 생성할 수 있는 N비트 해시의 예상 개수는 2개가^N 아니라 2개뿐입니다^N⁄2.이것은 암호화 해시 함수에 대한 생일 공격에 의해 악용되며, 이것이 해시 테이블의 소수의 충돌이 모든 실제적인 목적을 위해 불가피한 이유입니다.

생일 문제의 배후에 있는 이론은 조 슈나벨이^[17] 호수의 물고기 개체수의 크기를 추정하기 위해 포획-재포획 통계라는 이름으로 사용했습니다.

여러 유형의 사용자에게 일반화

기본적인 문제는 모든 시행을 하나의 "유형"으로 간주합니다.생일 문제는 임의의 종류를 고려하는 것으로 일반화되었습니다.^[18]가장 간단한 확장으로 남성과 여성이라고 하는 두 가지 유형의 사람이 있으며, 문제는 적어도 한 명의 남성과 한 명의 여성 사이에 생일이 공유될 확률을 특징짓는 것이 됩니다.(두 남자 또는 두 여자 간의 공유 생일은 포함되지 않습니다.)여기서 공유 생일이 없을 확률은

${\displaystyle p_{0}={\frac {1}{d^{m+n}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(n,j)\prod _{k=0}^{i+j-1}d-k}$

여기서 d = 365와 S는 두 번째 종류의 스털링 수이다.따라서 원하는 확률은 1 - p입니다₀.

생일 문제의 이 변형은 총 인원 m + n에 대한 고유한 해가 없기 때문에 흥미롭습니다.예를 들어, 일반적인 50% 확률 값은 남성 16명, 여성 16명으로 구성된 32명 그룹과 여성 43명, 남성 6명으로 구성된 49명 그룹 모두에 대해 실현됩니다.

다른 생일문제

첫번째 시합

이와 관련된 질문은, 사람들이 한 번에 한 명씩 방에 들어갈 때, 어떤 사람이 이미 방에 있는 사람과 같은 생일을 가질 가능성이 가장 높은가 하는 것입니다.즉, p(n) - p(n - 1)의 최대값은 무엇입니까?정답은 20번입니다. 첫 경기에 상품이 있다면 가장 좋은 자리는 20번입니다.^{[citation needed]}

너와같은 생일

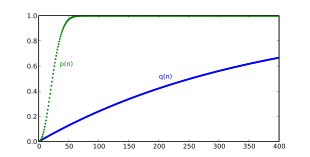
생일 문제에서는 두 사람 중 어느 쪽도 미리 선택하지 않습니다.대조적으로, 다른 사람들의 방에 있는 누군가가 특정한 사람(예를 들어, 당신)과 같은 생일을 가질 확률 q(n)은 다음과 같이 주어집니다.

${\displaystyle q(n)=1-\left ({\frac {365-1}{365}}\right)^{n}$

일반적으로 사용할 수 있는

${\displaystyle q(n;d)=1-\left ({\frac {d-1}{d}}\right)^{n}}$

d = 365의 표준 경우 n = 23을 대입하면 약 6.1%의 확률을 얻을 수 있으며, 이는 16의 경우 1회 미만입니다.n명의 방에 한 사람이 당신과 같은 생일을 가질 확률이 50% 이상이 되려면 n은 적어도 253 이상이어야 합니다.이 수치는 365/2 = 182.5보다 상당히 높은 수치입니다. 그 이유는 방에 있는 다른 사람들 사이에 생일 일치가 있을 가능성이 높기 때문입니다.

생일을 공유한 사람의 수

n명으로 이루어진 그룹에 속한 어느 한 사람의 경우, 위에서 설명한$$바와 같이 자신의 생일을 다른 사람과 공유할 확률은 $q{\displaystyle }$ (${\displaystyle }$n${\displaystyle }$- ${\displaystyle 1;}$ ${\displaystyle d)}$ ${\displaystyle q(n-1;d)}$입니다.생일을 공유하는 사람의 예상 수는 이제 해당 확률에 사람의 수(n)를 곱하면 쉽게 계산할 수 있으므로 다음과 같습니다.

${\displaystyle n\left(1-\left ({\frac {d-1}{d}}\right)^{n-1}\right)}$

(이 곱은 지시 변수의 기대 값의 선형성 때문에 이런 방식으로 수행될 수 있습니다.)이는 공유되지 않은(고유한) 생일을 가진 예상 사용자 수가 다음과 같음을 의미합니다.

${\displaystyle n\left ({\frac {d-1}{d}\right)^{n-1}}$

3명, 4명 등 다른 사람과 공유하는 예상 인원에 대해서도 유사한 공식을 도출할 수 있습니다.

생일이 될때까지 인원수

생일마다 필요한 예상 인원을 쿠폰 수집가의 문제라고 합니다.nH로_n 계산할 수 있으며, 여기서 H는_n n번째 고조파 수이다.365일 가능한 날짜(생일 문제)는 2365입니다.

니어매치

또 다른 일반화는 생일이 같은 경우 생일이 k일 이내인 n명의 그룹에서 적어도 한 쌍을 찾을 확률을 묻는 것입니다.^[19]

${\displaystyle {\begin{aligned}p(n,k,d)&=1-{\frac {(d-nk-1)!} {d^{n-1}{\bigl (}d-n(k+1){\bigr )}!}}\end{aligned}}$

일부 쌍이 k일 또는 그 이하로 분리된 생일을 가질 확률이 50% 이상이 되도록 필요한 사람의 수는 다음 표에 나와 있습니다.

k	n for = 365
0	23
1	14
2	11
3	9
4	8
5	8
6	7
7	7

따라서 단지 7명의 무작위한 사람들로 이루어진 그룹에서, 그들 중 2명이 서로의 일주일 안에 생일을 가질 가능성이 더 높습니다.^[19]

생일이 일정한 일수

생일이 하나 이상 있는 날 수

예상되는 다른 생일 수, 즉 최소 한 사람의 생일인 날짜 수는 다음과 같습니다.

${\displaystyle d-d\left ({\frac {d-1}{d}\right)^{n}$

다음은 아무도 생일이 아닌 예상 날짜 수에 따라 결정됩니다.

${\displaystyle d\left ({\frac {d-1}{d}\right)^{n}$

이 값은 특정한 날이 아무도 생일이 아닐 확률(d - 1/d)ⁿ
로부터 오는 것으로 기대 값의 선형성 때문에 쉽게 합산됩니다.

예를 들어 d = 365의 경우 22명일 때는 약 21개의 다른 생일을, 50명일 때는 46개의 다른 생일을 예상해야 합니다.1000명일 때 생일은 341명(미청구 생일 24명) 정도 됩니다.

생일이 2일 이상인 날 수

위의 내용은 어느 특정한 날에 생일이 있는 사람의 수에 대한 분포로부터 일반화할 수 있으며, 이는 확률이 1/d인 이항 분포입니다.그러면 관련 확률에 d를 곱하면 예상 일수가 나옵니다.예를 들어, 최소 2일(즉, 0 또는 1이 아닌)의 사용자 생일을 공유할 것으로 예상되는 날짜 수는 다음과 같습니다.

생일을 반복하는 사람의 수

[1,d]에서 임의로 선택된 k번째 정수가 위의 q(k - 1; d)와 같은 이전 선택을 반복할 확률입니다.n개의 정수가 동일하게^[20] 선택됨에 따라 선택 항목이 이전 선택을 반복할 것으로 예상되는 총 횟수

${\displaystyle \sum _{k=1}^{n}q(k-1;d)=n-d+d\left ({\frac {d-1}{d}}\right)^{n}$

이는 예상되는 생일 수에서 예상되는 다른 생일 수를 뺀 수와 같다고 볼 수 있습니다.

하나 이상의 공유 생일을 받는 평균 사용자 수

생일 문제의 대안적인 공식에서 생일이 같은 쌍을 찾는 데 필요한 평균 사람 수를 묻습니다.확률 함수 Pr[n명 이상의 공유 생일을 가진 사람]을 고려하면, 이 평균은 중위수를 요구하는 관습적인 공식과는 반대로 분포의 평균을 결정합니다.이 문제는 Donald Knuth가 그의 책 The Art of Computer Programming에서 분석한 여러 해싱 알고리즘과 관련이 있습니다.크기 M의 모집단에서 교체를 통해 균일하게 표본을 추출할 경우 일부 개체의 첫 번째 반복 표본 추출에 필요한 시행 횟수가 기대값 n = 1 + Q(M)임을 알 수 있습니다.

${\displaystyle Q(M)=\sum _{k=1}^{M}{\frac {M!}{(M-k)!M^{k}}}.$

함수를

${\displaystyle Q(M)=1+{\frac {M-1}{M}}+{\frac {(M-1)(M-2)}{M^{2}}+\cdots +{\frac {(M-1)(M-1)\cdots 1}{M^{M-1}}}$

스리니바사 라마누잔에 의해 연구되었으며 점근적 팽창을 가지고 있습니다.

${\displaystyle Q(M)\sim {\frac {\pi M}{2}}-{{\frac {1}{3}}+{\frac {1}{12}}{\sqrt {\frac {\pi}{2M}}-{\frac {4}{135M}}+\cdots.}$

M = 365일 1년 동안 생일이 같은 쌍을 찾는 데 필요한 평균 인원은 n = 1 + Q(M) ≈ 24.61659로 50% 확률에 필요한 인원인 23명보다 다소 많습니다.가장 좋은 경우는 2명이면 충분하고, 최악의 경우는 최대 M + 1 = 366명이면 충분합니다. 하지만 평균적으로 25명만 필요합니다.

지시 변수 랜덤 변수를 사용한 분석은 이 문제에 대해 더 간단하지만 근사적인 분석을 제공할 수 있습니다.^[23]방에 있는 k명의 각 쌍 (i, j)에 대해, $우리$는${\displaystyle }$1 ${\displaystyle \le }$ ${\displaystyle i}$ ≤${\displaystyle }$j ≤$$k {\$displaystyle 1\leq i\leq j\leq$ k$}$에 대해 지시자 난수 변수 X를_ij 다음과 같이 정의합니다$.$

X를 생일이 같은 개체의 쌍을 세는 랜덤 변수라고 가정합니다.

n = 365일 때 k = 28이면 생일이 같은 개체의 예상 쌍 수는 28 × 27/2 × 365 ≈ 1.0356입니다.따라서 최소 28명 이상의 짝을 지어 줄 것을 기대할 수 있습니다.

이 문제에 대한 비공식적인 시연은 호주의 총리 목록에서 할 수 있는데, 2017년^[update] 현재 29명의 총리가 있으며, 이 중 24대 총리인 폴 키팅과 초대 총리인 에드먼드 바튼은 같은 생일인 1월 18일을 공유하고 있습니다.

2014년 FIFA 월드컵에서 32명의 선수단은 각각 23명이었습니다.공식 선수 명단을 분석한 결과, 16개의 선수단이 생일을 함께 하는 선수들이 있었고, 이 5개의 선수단 중 2개의 선수단이 있었습니다.아르헨티나, 프랑스, 이란, 한국, 스위스가 각각 2쌍, 호주, 보스니아 헤르체고비나, 브라질, 카메룬, 콜롬비아, 온두라스, 네덜란드, 나이지리아, 러시아, 스페인, 미국이 각각 1쌍이었습니다.^[24]

Voracek, Tran 및 Formann은 대다수의 사람들이 같은 생일을 가질 확률을 달성하기 위해 필요한 사람들의 수를 현저하게 과대평가하고 특정 표본 크기가 주어졌을 때 같은 생일을 가질 확률을 현저하게 과소평가한다는 것을 보여주었습니다.^[25]추가적인 결과는 심리학과 학생들과 여성들이 카지노 방문객들/직원들 또는 남성들보다 그 일을 더 잘했지만, 그들의 추정치에 대해서는 자신감이 덜하다는 것을 보여주었습니다.

역문제

역문제는 고정 확률 p에 대해 확률 p(n)이 주어진 p보다 작은 가장 큰 n을 찾거나 확률 p(n)이 주어진 p보다 큰 가장 작은 n을 찾는 것입니다.^{[citation needed]}

d = 365에 대한 위의 공식을 취하면,

${\displaystyle n(p;365)\approx {\sqrt {730\ln \left ({\frac {1}{1-p}}\right)}}}.$

다음 표에는 몇 가지 샘플 계산이 나와 있습니다.

p	n	n↓	p(n↓)	n↑	p(n↑)
0.01	0.14178√365 = 2.70864	2	0.00274	3	0.00820
0.05	0.32029√365 = 6.11916	6	0.04046	7	0.05624
0.1	0.45904√365 = 8.77002	8	0.07434	9	0.09462
0.2	0.66805√365 = 12.76302	12	0.16702	13	0.19441
0.3	0.84460√365 = 16.13607	16	0.28360	17	0.31501
0.5	1.17741√365 = 22.49439	22	0.47570	23	0.50730
0.7	1.55176√365 = 29.64625	29	0.68097	30	0.70632
0.8	1.79412√365 = 34.27666	34	0.79532	35	0.81438
0.9	2.14597√365 = 40.99862	40	0.89123	41	0.90315
0.95	2.44775√365 = 46.76414	46	0.94825	47	0.95477
0.99	3.03485√365 = 57.98081	57	0.99012	58	0.99166

경계를 벗어나는 일부 값은 근사치가 항상 정확하지 않음을 보여주기 위해 채색되었습니다.

파티션문제

관련된 문제는 운영 연구에서 나온 배낭 문제의 변형인 파티션 문제입니다.일부 가중치는 균형 척도에 적용되며, 각 가중치는 1그램에서 100만 그램(1톤) 사이에서 임의로 선택된 정수 그램입니다.문제는 체중계의 균형을 맞추기 위해 보통 (즉, 확률이 1에 가까운) 왼쪽 팔과 오른쪽 팔 사이의 체중을 이동시킬 수 있느냐 하는 것입니다. (모든 체중의 합이 홀수 그램일 경우, 1 그램의 불일치는 허용됩니다.)두 개 또는 세 개의 가중치만 있는 경우에는 정답이 없음이 분명합니다. 비록 몇 가지 조합이 효과가 있지만, 임의로 선택된 세 개의 가중치 조합의 대부분은 그렇지 않습니다.만약 매우 많은 무게가 있다면, 답은 분명히 그렇다 입니다.문제는, 얼마나 많은 사람들이 충분한가 하는 것입니다.즉, 불가능한 경우와 동일하게 균형을 맞출 가능성이 있는 가중치의 수는 몇 개입니까?

종종, 사람들의 직관은 정답이 10만 이상이라는 것입니다.대부분의 사람들의 직관은 그것이 수천 또는 수만 개라는 것이고, 반면 다른 사람들은 그것이 적어도 수백 개는 되어야 한다고 생각합니다.정답은 23입니다.^{[citation needed]}

그 이유는 정확한 비교는 왼쪽과 오른쪽으로 나뉜 무게의 파티션 수이기 때문입니다.N개의 무게에 대해 두 개의^{N − 1} 다른 파티션이 있으며, 왼쪽 합에서 오른쪽 합을 뺀 것은 각 파티션에 대한 새로운 무작위 수량으로 생각할 수 있습니다.가중치 합의 분포는 500000N과 너비 10000000000 √N에서 피크가 있는 가우시안과 대략 2가 1000000 √N과 같을 때 전이가 발생합니다.2개는^{23 − 1} 약 400만개인데 비해 분포 폭은 500만개에 불과합니다.^[26]

소설속에서

아서 C. 클라크의 1961년 소설 '달의 추락'은 무기한 지하에 갇힌 주인공들이 생일을 축하하며 생일 문제의 타당성을 논의하는 대목을 담고 있습니다.한 물리학 승객이 말한 것처럼, "만약 당신이 24명 이상의 그룹을 가지고 있다면, 그들 중 두 명의 생일이 같은 것보다 확률이 더 높습니다."결국 22명의 참석자 중 두 인물이 같은 생일인 5월 23일을 함께 한다는 사실이 밝혀집니다.

메모들

참고문헌

서지학

• Abramson, M.; Moser, W. O. J. (1970). "More Birthday Surprises". American Mathematical Monthly. 77 (8): 856–858. doi:10.2307/2317022. JSTOR 2317022.
• Bloom, D. (1973). "A Birthday Problem". American Mathematical Monthly. 80 (10): 1141–1142. doi:10.2307/2318556. JSTOR 2318556.
• Kemeny, John G.; Snell, J. Laurie; Thompson, Gerald (1957). Introduction to Finite Mathematics (First ed.).
• Klamkin, M.; Newman, D. (1967). "Extensions of the Birthday Surprise". Journal of Combinatorial Theory. 3 (3): 279–282. doi:10.1016/s0021-9800(67)80075-9.
• McKinney, E. H. (1966). "Generalized Birthday Problem". American Mathematical Monthly. 73 (5): 385–387. doi:10.2307/2315408. JSTOR 2315408.
• Mosteller, F. (1962). "Understanding the birthday problem". The Mathematics Teacher. Springer Series in Statistics. 55 (5): 322–325. doi:10.1007/978-0-387-44956-2_21. ISBN 978-0-387-20271-6. JSTOR 27956609.
• Schneps, Leila; Colmez, Coralie (2013). "Math error number 5. The case of Diana Sylvester: cold hit analysis". Math on Trial. How Numbers Get Used and Abused in the Courtroom. Basic Books. ISBN 978-0-465-03292-1.
• Sy M. Blinder (2013). Guide to Essential Math: A Review for Physics, Chemistry and Engineering Students. Elsevier. pp. 5–6. ISBN 978-0-12-407163-6.

외부 링크

• 윤년 생일을 설명하는 생일 역설
• Weisstein, Eric W. "Birthday Problem". MathWorld.
• 역설을 설명하는 유머러스한 기사
• SOCR 에듀머티리얼즈 활동 생일 실험
• 생일 문제의 이해 (더 나은 설명)
• 2012년 유로 생일. 생일 문제.생일 역설의 실용적인 축구 예.
• Grime, James. "23: Birthday Probability". Numberphile. Brady Haran. Archived from the original on 2017-02-25. Retrieved 2013-04-02.
• 볼프람 알파의 생일 문제 확률 계산