확률론
쿠폰 수를 나타내는 그래프, n 대 모든 쿠폰을 수집하는 데 필요한 시행 횟수(예: 시간), E (T ) 확률론 에서 쿠폰수집자 의 문제는 "모든 쿠폰을 모아서 이기는" 콘테스트를 기술한다. 다음과 같은 질문을 던진다. 시리얼 브랜드의 각 박스에 쿠폰이 들어 있고, 쿠폰 종류가 n개라면 , 모든 쿠폰을 모으기 위해 t박스 이상을 사야 할 확률은 얼마인가? 대안은 다음과 같다: 쿠폰이 n개인 경우, 각 쿠폰을 한 번 이상 추첨하기 전에 교체 쿠폰을 몇 개까지 추첨해야 할 것으로 예상하십니까? 문제의 수학적 분석에 따르면 θ n log n ) {\displaystyle \Teta (n\log(n)}} 예상 횟수 가 증가한다는 것을 알 수 있다. [a] 들어 , n = 50일 경우, 쿠폰 50장을 모두 회수하는 데 평균 약 225회의[b]
해결책 기대치 계산 시간 T 는 모든 n개 의 쿠폰을 모으는 데 필요한 추첨 횟수로 하고, i - 1 쿠폰을 모은 후에는 i번째i 그러면 T t 1 ⋯ t n {\ displaystyle T=t_{1}+\cdots +t_{n T 와 t 를i 랜덤 변수 로 생각한다. 새 쿠폰을 수집할 확률은 p n i n i 1n {\ displaystyle p_{i}={\frac {n-(i-1)}{n}={\frac{n-i+1}{n}}}}} . 따라서 t i {\ displaystyle t_{i}} 기대치 1 p n i {\ displaystyle {\frac 1}{p_{i}}}={\frac {n}{n-i+1}}}}}}}} 가진 기하학적 분포가. 기대치 :
E ( T ) = E ( t 1 + t 2 + ⋯ + t n ) = E ( t 1 ) + E ( t 2 ) + ⋯ + E ( t n ) = 1 p 1 + 1 p 2 + ⋯ + 1 p n = n n + n n − 1 + ⋯ + n 1 = n ⋅ ( 1 1 + 1 2 + ⋯ + 1 n ) = n ⋅ H n . {\displaystyle{\begin{정렬}\operatorname{E}(T)&,{}=\operatorname{E}(t_{1}+t_{2}+\cdots +t_{n})\\&,{}=\operatorname{E}(t_{1})+\operatorname{E}(t_{2})+\cdots+\operatorname{E}(t_{n})\\&,{}={\frac{1}{p_{1}}}+{\frac{1}{p_{2}}}+{\frac{1}{p_{n}}}\\& +\cdots,{}={\frac{n}{n}}+{\frac{n}{n-1}};{}=n\ +{\frac{n}{1}}\\& +\cdots.cdot \left({\frac{1 }}{1}+{\frac {1}{2}}+\cdots +{\frac {1}{n}\오른쪽)\ \&{}=n\cdot H_{n}. \end{정렬}}} 여기서 H 는n n번째 고조파 수입니다 . 고조파 숫자의 점근법 을 사용하여 다음을 얻는다.
E ( T ) = n ⋅ H n = n 통나무를 하다 n + γ n + 1 2 + O ( 1 / n ) , {\displaystyle \operatorname {E}(T)=n\cdot H_{n}=n\log n+\gamma n+{1}{1}:{2}}+O(1/n),} 여기서 γ ≈ .5772156649 {\displaystyle \gamma 약 0.5772156649} 오일러-마스체로니 상수이다.
마르코프 부등식 을 사용하여 원하는 확률에 바인딩:
P ( T ≥ c n H n ) ≤ 1 c . {\displaystyle \operatorname {P}(T\geq cnH_{n})\leq {\frac {1}{c}. } 위 내용은 이미 쿠폰 일부를 회수했을 때 케이스 처리를 위해 약간 수정할 수 있다. k 를 이미 수집된 쿠폰의 개수로 설정한 후:
E ( T k ) = E ( t k + 1 + t k + 2 + ⋯ + t n ) = n ⋅ ( 1 1 + 1 2 + ⋯ + 1 n − k ) = n ⋅ H n − k {\displaystyle {\begin{aligned}\operatorname {E} (T_{k})&{}=\operatorname {E} (t_{k+1}+t_{k+2}+\cdots +t_{n})\\&{}=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n-k}}\right)\ \&{}=n\cdot H_{n-k}\end{arged}}}} 그리고 0 {\displaystyle k=0}
분산 계산 랜덤 변수 t 의i 독립성을 사용하여 다음을 얻는다.
VAR ( T ) = VAR ( t 1 + ⋯ + t n ) = VAR ( t 1 ) + VAR ( t 2 ) + ⋯ + VAR ( t n ) = 1 − p 1 p 1 2 + 1 − p 2 p 2 2 + ⋯ + 1 − p n p n 2 < ( n 2 n 2 + n 2 ( n − 1 ) 2 + ⋯ + n 2 1 2 ) = n 2 ⋅ ( 1 1 2 + 1 2 2 + ⋯ + 1 n 2 ) < π 2 6 n 2 {\displaystyle{\begin{정렬}\operatorname{바르}(T)&,{}=\operatorname{바르}(t_{1}+\cdots{n+t_})\\&,{}=\operatorname{바르}(t_{1})+\operatorname{바르}(t_{2})+\cdots+\operatorname{바르}(t_{n})\\&,{}={\frac{1-p_{1}}{p_{1}^{2}}}+{\frac{1-p_{2}}{p_{2}^{2}}};{}<, \left({\frac{{2n^}}{n^{2}}}++{\frac{1-p_{n}}{p_{n}^{2}}}\\& +\cdots.{\frac{{2n^}}{(n-1 )^{2}}:}+\cdots +{\frac{n^{2}}:{1^{2}}\오른쪽)\ \&{}=n^{2}\cdot \left\frac {1}{1^{2}}:}+{1}{1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}\오른쪽)\\ \&{}<{\frac {\pi^{2}}:{6}n^{2}\end{aigned}}}}} since π 2 6 = 1 1 2 + 1 2 2 + ⋯ + 1 n 2 + ⋯ {\displaystyle {\frac {\pi ^{2}}{6}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\cdots +{\frac {1}{n^{2}}}+\cdots } Basel problem ).
체비셰프 부등식 을 사용하여 원하는 확률 제한:
P ( T − n H n ≥ c n ) ≤ π 2 6 c 2 . {\displaystyle \operatorname {P} \left(T-nH_{n}\geq cn\right)\leq {\frac {\pi^{2}}{6c^{2}}. } 꼬리 추정치 상부 꼬리에 대한 더 강력한 꼬리 추정치는 다음과 같이 구한다. Z r {\ displaystyle {Z}_{i}^{r}}} 번째 {\displaystyle i} 그러면
P [ Z i r ] = ( 1 − 1 n ) r ≤ e − r / n . {\displaystyle {\reasoned} P\왼쪽[{Z}_{i}^{r}\오른쪽]=\왼쪽(1-{\frac {1}{n}\오른쪽)^{r}\leq e^{-r/n} \end{정렬}}} Thus, for r = β n log n {\displaystyle r=\beta n\log n} P [ Z i r ] ≤ e ( − β n log n ) / n = n − β {\displaystyle P\left[{Z}_{i}^{r}\right]\leq e^{(-\beta n\log n)/n}=n^{-\beta }} n {\displaystyle n}
P [ T > β n 통나무를 하다 n ] = P [ ⋃ i Z i β n 통나무를 하다 n ] ≤ n ⋅ P [ Z 1 β n 통나무를 하다 n ] ≤ n − β + 1 . {\displaystyle {\reasoned} P\좌[T]\베타 n\log n\우]= P\\왼쪽[\bigcup _{Z}_{i}^{\beta n\log n}\right]\leq n\cdot P[{Z}_{1}^{\beta n}}}\leq n^{-\beta +1}. \end{정렬}}} 확장 및 일반화 P ( T < n 통나무를 하다 n + c n ) → e − e − c , 로서 n → ∞ . {\displaystyle \operatorname {P}(T<n\log n+cn)\to e^{-e^{-c},{\text{} as }}}. 도날드 J. 뉴먼과 로렌스 셰프는 각 쿠폰 의 m 카피를 수집해야 할 때 쿠폰 수집기의 문제를 일반화했다.각 쿠폰의 m 복사본 이 수집되는 것은 T 가m 처음이다. 그들은 이 경우에 대한 기대가 다음을 충족한다는 것을 보여주었다. E ( T m ) = n 통나무를 하다 n + ( m − 1 ) n 통나무를 하다 통나무를 하다 n + O ( n ) , 로서 n → ∞ . {\displaystyle \operatorname {E}(T_{m})=n\log n+(m-1)n\log \log n+O(n),{\text{{}를 }n\n\to \inflt.}로 표시 여기 m은 고정되어 있다.m = 1일 때 우리는 기대치에 대한 더 이른 공식을 얻는다.Erdős 및 Rényi에 의한 일반적인 일반화: P ( T m < n 통나무를 하다 n + ( m − 1 ) n 통나무를 하다 통나무를 하다 n + c n ) → e − e − c / ( m − 1 ) ! , 로서 n → ∞ . {\displaystyle \operatorname {P} \left(T_{m}) \log n+(m-1)n\log n+cn\right)\to e^{-e^{-c}/(m-1)!},{\text{}n\n\to \fto.}} E ( T m ) = ∫ 0 ∞ ( 1 − ∏ i = 1 m ( 1 − e − p i t ) ) d t . {\displaystyle \operatorname {E}(T_{m})=\int _{0}^{\infit }\좌측(1-\prod _{i=1}^{m}\좌측(1-e^{p_{i}t}\오른쪽)dt. } 이것은 와 같다. E ( T m ) = ∑ q = 0 m − 1 ( − 1 ) m − 1 − q ∑ J = q 1 1 − P J {\displaystyle \operatorname {E}(T_{m})=\sum _{q=0}^{m-1-q}\sum _{J =q}{\frac {1}{1-P_{J}}}}}}}}}}}}}}}}} 여기서 m 은 수집할 쿠폰의 수를 나타내며, P 는J 쿠폰 J 세트의 쿠폰을 받을 확률을 나타낸다. 참고 항목 메모들 ^ 여기서 그리고 이 글 전체에서 "log"는 어떤 다른 베이스에 대한 로그가 아닌 자연 로그 를 가리킨다. 여기서 θ을 사용하면 큰 o 표기법 이 발동된다. ^ E(50) = 50(1 + 1/2 + 1/3 + … + 1/50) = 224.9603, 쿠폰 50개를 모두 회수할 것으로 예상되는 시험 횟수 이 예상 숫자에 대한근사치 로그 n γn 1 2 {\displaystyle log +\gamma 1/2} 50 로그 50 50 γ 2 ≈ 195.6011 28 . 8608 0 ≈ 224.9619 {\displaystyle 50\log 50+50\buffer +1/2\ 약 195.6011+28.8608+0. 5\ 224.9619
참조 ^ Flajolet, Philippe; Gardy, Danièle; Thimonier, Loÿs (1992), "Birthday paradox, coupon collectors, caching algorithms and self-organizing search", Discrete Applied Mathematics , 39 (3): 207–229, CiteSeerX 10.1.1.217.5965 doi :10.1016/0166-218x(92)90177-c Blom, Gunnar; Holst, Lars; Sandell, Dennis (1994), "7.5 Coupon collecting I, 7.6 Coupon collecting II, and 15.4 Coupon collecting III", Problems and Snapshots from the World of Probability ISBN 0-387-94161-4 MR 1265713 Dawkins, Brian (1991), "Siobhan's problem: the coupon collector revisited", The American Statistician , 45 (1): 76–82, doi :10.2307/2685247 , JSTOR 2685247 Erdős, Paul ; Rényi, Alfréd (1961), "On a classical problem of probability theory" (PDF) , Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei , 6 : 215–220, MR 0150807 Laplace, Pierre-Simon (1812), Théorie analytique des probabilités , pp. 194–195Newman, Donald J. ; Shepp, Lawrence (1960), "The double dixie cup problem", American Mathematical Monthly 67 (1): 58–61, doi :10.2307/2308930 , JSTOR 2308930 , MR 0120672 Flajolet, Philippe ; Gardy, Danièle; Thimonier, Loÿs (1992), "Birthday paradox, coupon collectors, caching algorithms and self-organizing search" , Discrete Applied Mathematics , 39 (3): 207–229, doi :10.1016/0166-218X(92)90177-C , MR 1189469 Isaac, Richard (1995), "8.4 The coupon collector's problem solved", The Pleasures of Probability Undergraduate Texts in Mathematics , New York: Springer-Verlag, pp. 80–82, ISBN 0-387-94415-X MR 1329545 Motwani, Rajeev ; Raghavan, Prabhakar (1995), "3.6. The Coupon Collector's Problem", Randomized algorithms ISBN 9780521474658 MR 1344451 외부 링크 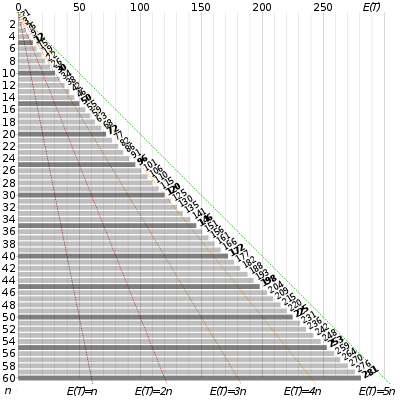










 (가) 되면 원래의 결과가 나온다.
(가) 되면 원래의 결과가 나온다. 





![{\displaystyle {\begin{aligned}P\left[{Z}_{i}^{r}\right]=\left(1-{\frac {1}{n}}\right)^{r}\leq e^{-r/n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c12757cabf87eff67732f4ea2e2f3042b8d2042)

![P\left [ {Z}_i^r \right ] \le e^{(-\beta n \log n ) / n} = n^{-\beta}](https://wikimedia.org/api/rest_v1/media/math/render/svg/916bd3a3939a0a68c3c412c893da118eb58826c5)

![{\displaystyle {\begin{aligned}P\left[T>\beta n\log n\right]=P\left[\bigcup _{i}{Z}_{i}^{\beta n\log n}\right]\leq n\cdot P[{Z}_{1}^{\beta n\log n}]\leq n^{-\beta +1}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26b6afb27c12cc574efc8ad9f6c6524da3ba8adc)









