전자 필터 위상

기본 필터 토폴로지는 저역 통과 전송 기능의 불균형 활성 구현을 달성하기 위해 op-amp의 피드백 경로에 캐패시터를 도입한다.

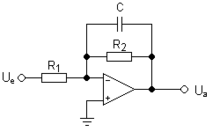
전자 필터 토폴로지는 사용되는 구성 요소의 값뿐만 아니라 해당 구성 요소가 연결되는 방식만 고려하지 않고 전자 필터 회로를 정의한다.

필터 설계는 주로 필터 회로의 위상이 아닌 전달 기능에 의해 특성화된다.전달 함수는 선형 또는 비선형일 수 있다.일반적인 선형 필터 전송 함수의 유형은 하이패스, 로우패스, 밴드패스, 밴드거부 또는 노치 및 올패스 입니다.필터에 대한 전송 기능을 선택한 후, 그러한 프로토타입 필터를 구현하기 위한 특정 토폴로지를 선택하여 예를 들어 Sallen-Key 토폴로지를 사용하여 Butterworth 필터를 설계할 수 있다.

필터 위상은 수동형과 능동형으로 나눌 수 있다.패시브 토폴로지는 저항기, 캐패시터, 인덕터 등 패시브 구성 요소만으로 구성된다.활성 위상에는 전력이 필요한 활성 구성 요소(트랜지스터, op 암페어 및 기타 집적 회로 등)도 포함된다.또한 토폴로지는 균형 잡힌 회로에서 사용할 때 불균형 형태로 또는 균형 잡힌 형태로 구현될 수 있다.전자 믹서와 스테레오 사운드와 같은 구현에는 동일한 회로의 배열이 필요할 수 있다.

패시브 토폴로지

패시브 필터는 오래전부터 개발 및 사용되어 왔다.대부분은 "섹션"이라고 불리는 단순한 2포트 네트워크로부터 만들어진다.섹션은 적어도 하나의 직렬 구성 요소와 션트 구성 요소를 가져야 한다는 것 외에는 공식 정의가 없다.섹션은 항상 "캐스케이드" 또는 "데이지 체인" 토폴로지로 연결되며, 동일한 섹션 또는 완전히 다른 섹션의 추가 복사본으로 구성된다.직렬 및 병렬 임피던스의 규칙은 직렬 구성요소 또는 션트 구성요소로만 구성된 두 개의 섹션을 단일 섹션으로 결합할 것이다.

1, 2개의 필터 섹션으로만 구성된 일부 패시브 필터에는 불균형 필터인 L-섹션, T-섹션, π-섹션, 그리고 균형이 잡힌 C-섹션, H-섹션, 박스섹션 등 특별한 이름이 붙는다.모든 것은 매우 간단한 "사다리" 위상 위에 구축된다(아래 참조).페이지 하단의 차트는 이러한 다양한 토폴로지를 일반 상수 k 필터 측면에서 보여준다.

네트워크 합성을 사용하여 설계된 필터는 각 섹션에서 구성요소 값이 변경될 수 있지만 일반적으로 가장 단순한 형태의 L-섹션 위상 형태를 반복한다.반면에 이미지 설계 필터는 위상이 다를 수 있고 보다 복잡한 섹션을 사용하는 경향이 있지만 섹션마다 동일한 기본 구성요소 값을 유지한다.

L-섹션은 결코 대칭적이지 않지만 두 개의 L-섹션이 대칭 토폴로지를 형성하고 다른 많은 섹션은 형태에서 대칭이다.

사다리 위상

빌헬름 카우어(타원형 필터의 발명가)의 이름을 따서 종종 카우어 위상이라고 불리는 래더 위상은 사실 조지 캠벨(상수 k 필터의 발명가)에 의해 처음 사용되었다.캠벨은 1922년에 출판되었지만, 이것 이전에 분명히 얼마 동안 위상을 사용하고 있었다.카우어는 포스터(1924년)의 작품에서 영감을 받아 사다리(1926년 간행)를 처음으로 집어들었다.기본 사다리 위상에는 불균형과 균형이라는 두 가지 형태가 있다.카우어 위상은 보통 불균형 사다리 위상이라고 여겨진다.

사다리 네트워크는 계단식 비대칭 L-섹션(균형화되지 않음) 또는 C-섹션(균형화됨)으로 구성된다.로우패스 형태의 토폴로지는 직렬 인덕터와 분로 캐패시터로 구성된다.다른 밴드폼은 저역 통과 위상에서 변환된 동일한 단순한 위상이다.변환된 네트워크는 출발 네트워크의 듀얼 네트워크인 경우 직렬 임피던스의 이중 네트워크인 션트 입력을 가지며, 이는 직렬 인덕터와 션트 캐패시터의 경우에 해당된다.

이미지 필터 섹션

불균형
L 하프 섹션	T 단면	π 단면

사다리망

균형 잡힌
C 반쪽 단면	H 섹션		상자 단면

사다리망

X 단면(중간 T-파생)		X 섹션(중간-중간-파생)

N.B.	교과서나 설계도면은 보통 불균형한 구현을 보여주지만, 통신에서는 균형 잡힌 선으로 사용할 때 균형 잡힌 구현으로 설계를 전환해야 하는 경우가 많다.	편집하다

수정된 사다리 위상

m-수직 위상

이미지 필터 설계는 일반적으로 기본 래더 위상의 수정을 사용한다.오토 조벨이 발명한 이러한 토폴로지는 그 기반이 되는 사다리와 같은 패스밴드를 가지고 있지만, 임피던스 매칭, 스톱밴드 거부, 패스밴드 대 스톱밴드 전환 가파도 등의 일부 파라미터를 개선하기 위해 전송기능을 수정한다.^[1]일반적으로 설계는 단순한 래더 위상에 일부 변환을 적용한다. 즉, 결과 위상은 사다리와 유사하지만 션트 입력이 직렬 임피던스의 이중 네트워크라는 규칙을 더 이상 준수하지 않는다. 즉, 구성품수가 높을수록 항상 더 복잡해진다.이러한 토폴로지는 다음을 포함한다.

m-type (m-deared) 필터는 지금까지 가장 일반적으로 사용되는 수정 이미지 래더 위상이다.각각의 기본 사다리 위상에 대해 두 가지 m형 위상이 있다; 시리즈 파생 위상과 분절 파생 위상이 그것이다.이들은 서로 전송 기능은 동일하지만 영상 임피던스는 다르다.필터를 둘 이상의 통과 대역으로 설계하는 경우, m형 토폴로지는 각 통과 대역에서 유사한 주파수 영역 응답을 갖는 필터가 된다.서로 같지 않은 매개변수₁ m, m₂, m₃ 등을 이용하여 둘 이상의 패스밴드를 가진 필터에 대해 m형 토폴로지를 일반화할 수 있어 주파수 스펙트럼의 다른 부분에서 차이가 나는 대역형_n^[2] 필터가 있다.

mm형 위상은 이중 m형 설계로 생각할 수 있다.m타입과 마찬가지로 밴드폼은 동일하지만 더욱 개선된 전송특성을 제공한다.그러나, 임피던스와 일치하는 이유로 동일한 필터에 기본 래더와 m-타입 섹션이 일반적으로 요구되는 것은 물론, 구성요소 수와 복잡성 증가로 인해 거의 사용되지 않는 설계다.일반적으로 복합 필터에서만 찾을 수 있다.

브리지-T 토폴로지

하이엔드 롤오프를 수정하는 데 사용되는 일반적인 브리지-T 조벨 네트워크 이퀄라이저

Zobel 상수 저항^[3] 필터는 모든 주파수에서 일정한 입력 저항을 가지며 섹션 설계 시 저항성 구성요소를 사용한다는 점에서 구별되는 다른 필터 유형과 다소 다른 위상(위상)을 사용한다.이러한 설계의 구성 요소와 섹션 수가 더 높으면 대개 애플리케이션 평준화로 사용을 제한한다.일반적으로 상수 저항 필터와 관련된 위상은 브리지-T 및 그 변형이며, 모두 조벨 네트워크 기사에 설명되어 있다.

브리지-T 위상
균형 브리지-T 위상
개방 회로 L-단면 위상
단락 L-단면 위상
균형 개방 회로 C-단면 위상
균형 단락 C-단면 위상

브리지-T 위상은 신호 지연을 발생시키기 위한 섹션에도 사용되지만 이 경우 설계에 저항성 구성요소가 사용되지 않는다.

격자 위상

격자 위상 X 단면 위상 보정 필터

T-섹션(사다리 위상에서)과 Bridge-T(조벨 위상에서)는 격자 위상 필터 섹션으로 변환할 수 있지만, 두 경우 모두 구성 요소 개수와 복잡성이 높다.격자 필터(X-섹션)의 가장 일반적인 적용은 위상 균등화에 사용되는 올패스 필터에 있다.^[4]

T 섹션과 브리지-T 섹션은 항상 X 섹션으로 변환할 수 있지만, 변환에서 발생하는 인덕턴스와 캐패시턴스의 음수 값의 가능성 때문에 역이 항상 가능한 것은 아니다.

격자 위상은 보다 친숙한 교량 위상과 동일하며, 그 차이는 위상, 회로 또는 기능의 실제 차이보다는 페이지에 그려진 표현일 뿐이다.

활성 위상

다중 피드백 토폴로지

다중 피드백 토폴로지 회로

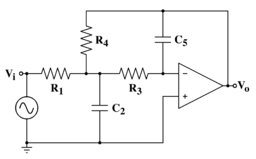
다중 피드백 토폴로지는 전자 필터 토폴로지로 전송 기능에 극 2개를 추가하여 전자 필터를 구현하는 데 사용된다.두 번째 순서의 로우패스 필터에 대한 회로 토폴로지 다이어그램은 오른쪽 그림에 나와 있다.

모든 2차 선형 필터와 마찬가지로 다중 피드백 토폴로지 회로의 전송 기능은 다음과 같다.

H(s)={\frac {V_{o}}{V_{i}}}=-{\frac {1}{As^{2}+Bs+C}}={\frac {K{\omega _{0}}^{2}}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

.

MF 필터에서

A=(R_{1}R_{3}C_{2}C_{5}\,

B=R_{3}C_{5}+R_{1}C_{1}+R_{1}R_{3}C_{5}/R_{4}\,

C=R_{1}/R_{4}\,

{\

C_{5}}}}}

은

Q={\frac {{\sqrt {R_{3}R_{4}C_{2}C_{5}}}}{(R_{4}+R_{3}+|K|R_{3})C_{5}}}

(는) Q 인자다.

K=-R_{4}/R_{1}\,

=

K=-R_{4}/R_{1}\,

-

K=-R_{4}/R_{1}\,

K=-R_{4}/R_{1}\,

/

K=-R_{4}/R_{1}\,

1

displaystyle

K

=-R_{4}/R_{1}\,}

은

K=-R_{4}/R_{1}\,

(는) DC 전압 게인이다.

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

=

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

=

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

/

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

3

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

C

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

\omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

5

{\

은

\omega _{{0}}=2\pi f_{{0}}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}

코너 주파수 모서리 주파수

원하는 필터 특성을 달성하기 위한 적절한 구성요소 값을 찾기 위해, 대체 Sallen-Key 토폴로지의 설계 선택 섹션에서와 유사한 접근방식을 따를 수 있다.

바이쿼드 필터 위상

바이쿼드 필터의 디지털 구현에 대해서는 디지털 바이쿼드 필터를 참조하십시오.

바이쿼드 필터는 2차 함수의 비율인 전송 함수를 구현하는 선형 필터의 일종이다.바이쿼드라는 이름은 바이쿼드어의 줄임말이다.2차 필터 위상은 MFB 또는 Salen-Key와 같이 바이쿼드라고 할 수 있다.^[5]^[6]그러나, 특정한 "비쿼드" 위상도 있다.'3의 고리' 회로라고도 한다.^{[citation needed]}

바이쿼드 필터는 일반적으로 활성화되며 단일 증폭기 바이쿼드(SAB) 또는 2-통합기-루프 토폴로지로 구현된다.

SAB 토폴로지는 피드백을 사용하여 복잡한 극과 아마도 복잡한 0을 생성한다.특히 피드백은 적절한 필터 특성을 생성하기 위해 RC 회로의 실제 극을 이동시킨다.
2-적분자-루프 위상은 2차 전달 함수의 재배열에서 도출된다.재배열은 한 신호를 다른 신호, 그 적분 및 적분 적분 합계와 동일시한다.즉, 재배열로 상태변수 필터 구조가 드러난다.다른 상태를 출력으로 사용함으로써, 어떤 종류의 2차 필터도 구현할 수 있다.

SAB 토폴로지는 구성요소 선택에 민감하며 조정하기가 더 어려울 수 있다.따라서 일반적으로 바이쿼드라는 용어는 2-적분자-루프 상태 변수 필터 토폴로지를 가리킨다.

토우토마스 필터

그림 1.공통 토우토마스 바이쿼드 필터 토폴로지.

예를 들어, 그림 1의 기본 구성은 출력 신호를 어디서 가져왔는지에 따라 저역 통과 또는 대역 통과 필터로 사용할 수 있다.

2차 저역 통과 전송 기능은

{\displaystyle H(s)={\frac {G_{\mathrm {lpf}}{{0}^{0}}}{{0}}}{{0}}}}{{0}}}}}{0}}}}}}:{0}}}:{0}:{0}}}}2}}:

여기서 저역 통과 게인 $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ = $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ - $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ / $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ ${\$ }:{1 $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ 2차 대역전송 기능은 다음과 같다.

H(s)={\frac {G_{\mathrm {bpf} }{\frac {\omega _{0}}{Q}}s}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

.

bandpass gain $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ f $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ = $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ - $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ / R $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ ${\$ 두 경우 모두

고유 주파수는 $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ Ω $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ = $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ / R $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ C 2 ${\$ }=1 $/{\sqrt{R_{$ 2} $R_{4}$ C_{1} $C_{2$
품질인자는 Q $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ = $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ 1 $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$ 2 ${\$ }R_{4} $C_{2}}}}}}}}}$ 입니다 $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{4}C_{2}}}}$

The bandwidth is approximated by $B=\omega _{0}/Q$ , and Q is sometimes expressed as a damping constant $\zeta =1/2Q$ . If a noninverting low-pass filter is required, the output can be taken at the output of the second operational amplifier, after the order of the second inte그래이터와 인버터가 전환되었다.비인버팅 대역 통과 필터가 필요한 경우, 두 번째 통합자와 인버터의 순서를 바꿀 수 있으며, 인버터의 작동 증폭기의 출력에서 얻은 출력이 된다.

아케르베르크-모스베르크 필터

그림 2.Akerberg-Mossberg 바이쿼드 필터 토폴로지.

그림 2는 필터 성능을 향상시키는 능동 보정 밀러 통합자를 사용하는 Akerberg-Mossberg 토폴로지로 알려진 Tow-Thomas 토폴로지의 변형을 보여준다.

살렌-키 위상

그림 1: 일반 Sallen-Key 필터 토폴로지

Salen-Key 디자인은 높은 Q와 패스밴드 이득 옵션을 가진 비인버링 2차 필터다.

참고 항목

메모들

^ 조벨, 1923년
^ 이러한 종류의 필터에는 보편적으로 인식되는 이름이 없다: Zobel(1923, 페이지 11)은 하나의 중간 지점 특성 임피던스를 변경하지 않고 사전 할당된 송신 및 감쇠 대역과 전파 상수 조절이 가능한 일반 파형 필터라는 제목을 사용했다.조벨은 매개변수를 m₁, m₂ 등으로 지칭하기 때문에 속기 일반 m-타입은_n 여기서 사용하기에 합리적인 용어인 것 같다.
^ 조벨, 1928년
^ 조벨, 1931년
^ "A Beginner's Guide to Filter Topologies". Maxim Integrated. Archived from the original on 2019-10-28. Retrieved 2021-07-30. This means Sallen-Key filters, state-variable variable filters, multiple feedback filters and other types are all biquads. There also is a "biquad" topology to help further confuse things.
^ Moschytz, George S. (2019). Analog circuit theory and filter design in the digital world : with an introduction to the morphological method for creative solutions and design. Cham, Switzerland. ISBN 978-3-030-00096-7. OCLC 1100066185. plethora of single-amplifier second-order active filter circuits … whose numerator and denominator are of second order, i.e., biquadratic; they are therefore referred to as “biquads”

참조

캠벨, G. A, "전파-필터의 물리적 이론", 벨 시스템 기술 저널, 1922년 11월, 1권 2, 페이지 1–32.
Zobel, O J, " 균일 및 복합 전기파 필터의 이론 및 설계", Bell System Technical Journal, Vol. 2권(1923).
포스터, R M, "반응도 정리", Bell System Technical Journal, Vol. 3, 페이지 259–267, 1924.
카우어, W. "Die Verwirklichung der Wechelstromwiderstande vorgeschriebener Fruenzabhengkeit", 17, 페이지 355–388, 1926.
Zobel, O J, "항상 저항성이 있는 전기 네트워크에서의 이탈 보정", Bell System Technical Journal, Vol. 7권(1928), 페이지 438.
Zobel, O J, 위상 변화 네트워크, 미국 특허 1 792 523은 1927년 3월 12일 출원, 1931년 2월 17일 발행되었다.

외부 링크

Wikimedia Commons의 전자 필터 토폴로지 관련 미디어

[1] 조벨, 1923년

[2] 이러한 종류의 필터에는 보편적으로 인식되는 이름이 없다: Zobel(1923, 페이지 11)은 하나의 중간 지점 특성 임피던스를 변경하지 않고 사전 할당된 송신 및 감쇠 대역과 전파 상수 조절이 가능한 일반 파형 필터라는 제목을 사용했다.조벨은 매개변수를 m₁, m₂ 등으로 지칭하기 때문에 속기 일반 m-타입은_n 여기서 사용하기에 합리적인 용어인 것 같다.

[3] 조벨, 1928년

[4] 조벨, 1931년

[5] "A Beginner's Guide to Filter Topologies". Maxim Integrated. Archived from the original on 2019-10-28. Retrieved 2021-07-30. This means Sallen-Key filters, state-variable variable filters, multiple feedback filters and other types are all biquads. There also is a "biquad" topology to help further confuse things.

[6] Moschytz, George S. (2019). Analog circuit theory and filter design in the digital world : with an introduction to the morphological method for creative solutions and design. Cham, Switzerland. ISBN 978-3-030-00096-7. OCLC 1100066185. plethora of single-amplifier second-order active filter circuits … whose numerator and denominator are of second order, i.e., biquadratic; they are therefore referred to as “biquads”

[1]

[2]

[3]

[4]

[5]

[6]

Search