깨우다

Wake
기타 용도는 Wake(동음이의)를 참조하십시오.
작은 보트에 의해 생성된 켈빈 웨이크 패턴
켈빈 웨이크 시뮬레이션 그림.

유체 역학에서 웨이크업(wake)은 다음과 같을 수 있다.

  • 이동하거나 정지된 둔체 바로 뒤에 있는 재순환 유량 영역. 점도로 인해 발생하며, 유량 분리 및 난류를 동반할 수 있다.
  • 유동 중 물체의 물체 하류 표면의 파동 패턴 또는 움직이는 물체(예: 배)에 의해 생성되는 파동 패턴은 자유 표면과 중력(또는 표면 장력) 위/아래 유체의 밀도 차이로 인해 발생한다.

점도로 인한 웨이크 효과

공기 중 원형 실린더 뒤쪽의 카르만 소용돌이 거리의 시각화; 유증기가 실린더 근처 공기로 방출됨을 통해 흐름이 가시화된다.

웨이크(Wake)는 유체를 통해 이동하는 고체 신체의 하류(흔히 난류)의 방해된 흐름의 영역으로, 유체의 몸 주위의 유체 흐름에 의해 발생한다.

아음속 외부 흐름에서 둔탁한 신체의 경우, 예를 들어 강하와 착륙 중에 아폴로나 오리온 캡슐이 있는 경우, 웨이크는 대량으로 분리되고 몸 뒤는 흐름이 몸 쪽으로 이동하는 역류 영역이다. 이러한 현상은 항공기의 풍동실험에서 흔히 관찰되며 낙하산 선이 역류 지역을 넘어 캐노피를 연장하지 않는 한 슈트가 팽창하지 못해 붕괴될 수 있기 때문에 낙하산 시스템이 관련되었을 때 특히 중요하다. 웨이크에 배치된 낙하산은 예상되는 드래그력을 감소시키는 동적 압력 결손을 겪는다. 이러한 모델링은 불안정한 흐름 효과 외에도 난류 모델링(예: RANS 대 LES 구현)과 관련된 불확실성을 가지고 있지만, 높은 충실도 계산 유체 역학 시뮬레이션은 웨이크 흐름을 모델링하기 위해 종종 수행된다. 적용 예로는 로켓 단계 분리 및 항공기 저장소 분리가 있다.

물 표면과 같은 밀도 차이에 의한 파동

물과 같은 불압축 유체(액체)에서는 수공이 매개체를 통과할 때 활 웨이크가 생성되는데, 매개체를 압축할 수 없기 때문에 대신 교체해야 해 파동이 발생한다. 모든 파형의 형태와 마찬가지로 대개 마찰이나 분산에 의해 에너지가 극복되거나 상실될 때까지 원천으로부터 바깥쪽으로 퍼져 나간다.

관심의 비차원 매개변수는 Froude 번호다.

인도양 남부의 슐레 암스테르담(왼쪽 아래, 구름의 삼각형 형성 '끝'에)을 계기로 한 파도 구름 패턴
후안 페르난데스 제도에서 구름 깨어난다.
클라우드 커버의 웨이크 패턴이 이스트 아일랜드, 일레 보조 코콘스, 슐레 데 핑구인스 위에 있음

켈빈 웨이크 패턴

수면을 가로질러 움직이는 물새와 배들은 웨이크 패턴을 생성하는데, 켈빈 경은 처음으로 수학적으로 설명했고 오늘날 켈빈 웨이크 패턴으로 알려져 있다.[1]

이 패턴은 V의 정점에 있는 웨이크 소스와 함께 쉐브론 V의 팔을 형성하는 두 개의 웨이크 라인으로 구성되어 있다. 충분히 느린 움직임의 경우 각 웨이크 라인은 아크신(1/3) = 19.47°에 의해 웨이크 소스의 경로에서 오프셋되며 경로에 약 53° 각진 깃털 모양의 웨이브로 구성된다.

V 내부(위에서 표시한 총개방 39° 중)는 가로 곡선 주로로 채워져 있으며, 각 원은 원호의 2배인 거리에서 경사로에 놓여 있는 지점을 중심으로 한 원의 호이다. 이 패턴은 상당한 범위의 값에 대한 웨이크 소스의 속도 및 크기와 무관하다.[2]

그러나 이 패턴은 약 0.5의 선체 Froude 번호 위에 있는 고속(전용), viz에서 변경된다. 그 후 소스의 속도가 증가하면 횡파가 감소하고 웨이크 패턴 내에서 파장의 최대 진폭 포인트가 두 번째 V를 형성하는데, 이는 소스의 속도가 증가함에 따라 더 좁아진다.[3]

이 패턴의 각도는 단순히 물의 본질적인 특성이 아니다. 점도가 낮은 모든 등방성 및 비압축성 액체는 동일한 현상을 보일 것이다. 더구나 이 현상은 난기류와 무관하다. 여기서 논의되는 모든 것은 이상적인 유동체, cf의 선형 이론에 근거한다. 공기파 이론.

패턴의 일부는 프로펠러 세척의 효과와 보트 선미 뒤쪽의 꼬리가 휘어지며, 보트는 점원이 아닌 큰 물체에 의해 가려질 수 있다. 물은 정지해 있을 필요는 없지만, 큰 강에서처럼 움직이고 있을 수 있으며, 이때 중요한 고려사항은 보트나 다른 물체에 대한 물의 속도다.

이 패턴은 심층수파의 분산 관계에서 따온 것으로, 흔히 다음과 같이 씌어 있다.

어디에

g = 중력장의 강도
Ω은 초당 라디안 단위의 각도 주파수다.
k = 미터당 라디안 단위로 각진 수

'딥(Deep)'은 파장의 절반 이상의 깊이를 의미한다. 이 공식은 심층수파의 그룹 속도가 위상 속도의 절반이며, 다시 파장의 제곱근으로 간다는 것을 암시한다. 웨이크 패턴에 중요한 두 가지 속도 매개변수는 다음과 같다.

v는 물의 상대 속도 및 각성을 유발하는 표면 물체다.
c는 파동의 위상 속도로서, 파동 주파수에 따라 변화한다.

표면 물체가 움직이면서 파장의 스펙트럼이 넓은 사인파의 합인 작은 장애를 연속적으로 발생시킨다. 가장 긴 파장을 가진 파장은 위상속도가 v보다 높고 주변 물속으로 분산돼 쉽게 관측되지 않는다. 그러나 v 또는 v 이하에서 위상 속도를 가진 다른 파형은 건설적인 간섭을 통해 증폭되고 가시적인 충격파를 형성하며 보트 위치의 정지 상태를 유지한다.

일반적인 오리털 웨이크

위상충격파 전방과 물체의 경로 사이의 각도 θ은 θ = arcsin(c/v) c/v > 1이나 < -1>일 경우, 이후 어떤 파동도 이전의 파동을 따라잡을 수 없고 충격파가 형성되지 않는다.

깊은 물속에서는 파장이 충분히 짧은 파장은 더 느리게 움직이기 때문에 천천히 움직이는 원천에서도 충격파가 형성된다. 이러한 충격파는 순진하게 예상할 수 있는 각도보다 더 날카롭다. 왜냐하면 그것은 건설적인 간섭의 영역을 지시하는 그룹 속도이고 깊은 물에서는 그룹 속도가 위상 속도의 절반이기 때문이다.

각자가 33°와 72° 사이의 각도를 가졌을 모든 충격파는 15°와 19° 사이의 각도를 가진 좁은 웨이크 밴드로 압축되며, 외측 가장자리(각도 아크신(1/3) = 19.47°)에서 가장 강력한 건설적 간섭을 가하여 V의 두 팔을 유명한 켈빈 웨이크 패턴으로 배치한다.

간결한 기하학적 구조는[4] 위의 모든 any에 대해 19.47°의 보트 경로인 이 그룹 쇼크 각도가 실제로 v, c 및 g와 독립적이라는 것을 현저하게 증명한다. 단지 그룹 속도가 위상 속도 c의 절반이라는 사실에 의존한다. 어느 행성에서나 저속 스위밍 물체는 "실효 마하 수" 3을 가지고 있다!

연속된 시간에 방출되는 교란의 봉투, G.B.의 그림 12.3 페이지 410. Whitam(1974) 선형 및 비선형 파동. 원은 파도를 나타낸다.

느린 수영선수들에게 낮은 Froude 수인 Lighthill-켈빈 쉐브론(웨지, V 패턴)의 개방이 보편적이라는 휘담 기하학적 주장은 다음과 같다. 정속 v로 오른쪽에서 왼쪽으로 움직이는 보트를 보고, 다양한 파장의 파장을 발산하며, 따라서 충격파를 위한 v(예: 소닉 붐 또는 체렌코프 방사선)일 때 관심 있는 wavenumber k와 위상 속도 c(k)를 고려한다. 동등하게, 그리고 보다 직관적으로 배의 위치를 고정시키고 강에 쌓이는 것처럼 반대 방향으로 물이 흐르게 한다.

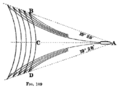
먼저 주어진 k에 초점을 맞추고, 고정 위치인 보트가 그들 모두에 접하는 표준 충격 쐐기(cf)에 조립되는 방출(상) 웨이브프론트에 초점을 맞춘다. 그림 12.3.

위와 같이 이들 쉐브론의 개구부는 위상충격파 앞쪽과 보트(물)의 경로 사이의 각도 θ = 아크신(c/v) π/2 - ψ에 따라 달라진다. 분명히 ψ은 k에 따라 증가한다. 그러나 이러한 위상 쉐브론은 보이지 않는다. 즉, 관찰되는 것은 해당 그룹 파장 발현이다.

연속적으로 방출되는 교란의 봉투, G.B.의 그림 12.2 페이지 409. Whitam(1974) 선형 및 비선형 파동. 여기서 ψ은 파원의 경로와 파장 전파 방향(파장 벡터 k) 사이의 각도로 원은 파장프롱트를 나타낸다.

특정 k에 대해 그림 12.3의 위상 원 중 하나를 고려하며, 과거 시간 t에 해당한다. 그림 12.2. 그것의 반지름은 QS이고, 위상 쉐브론 쪽은 그것에 접선된 PS이다. 분명히 PQ= vt와 SQ = ct = vt cosψ, 직각 PSQ가 직경 PQ의 반원 위에 S를 놓기 때문이다.

그러나 그룹 속도가 임의 및 전체 k에 대한 위상 속도의 절반이기 때문에 S에 해당하는 가시적(그룹) 교란 지점은 SQ의 중간점인 T가 된다. 마찬가지로, 현재 R을 중심으로 한 반원 위에 놓여 있는데, 여기서 분명히 R에서 방출되는 유효 그룹 파동인 RQ=PQ/4는 현재 반지름 vt/4이다.

유의하게, 보트의 경로, P에서 이 작은 원까지의 탄젠트 각도에 대한 결과의 파동전면 각도는 어떤 k, c, ψ, g 등에 대해서도 TR/PR=1/3의 사인(sine)이 분명히 있다. 놀랍게도, 심해 집단과 위상간 속도 관계를 제외한 문제의 거의 모든 매개변수가 사라졌다! 효과적인 집단 교란 방출체가 3V/4에서 더 느리게 움직인다는 점에 유의하십시오.

따라서 모든 관련 k와 ts를 합쳐서 효과적인 그림.12.3 충격 패턴을 구체화하면 범용 켈빈 웨이크 패턴이 발생한다: 완전한 가시적 쉐브론 각도는 2arcsin(1/3) 39 39°의 2배이다.

파동 발생 시 웨이브프론트는 53°로 대략 33°와 72°의 평균이다. 충격파 각도가 73°와 90° 사이인 파동 구성 요소는 V 내부를 지배한다. 이들은 결국 발생 지점과 현재 웨이크 소스의 위치 사이의 중간 지점에 도달한다. 이것은 호의 곡률을 설명한다.

33° 미만의 충격파 각도를 가진 매우 짧은 파장은 건설적인 간섭을 통해 진폭을 강화하는 메커니즘이 결여되어 있으며 대개 내부 횡파 위에 작은 파동으로 보인다.

갤러리

  • 고산호수를 건너는 배(Koenigsee)의 기상 (Koenigsee)

  • 선박 웨이크업 39°

  • 천천히 움직이는 두 척의 배들이 깨어난다. 가까이 있는 보트는 일련의 직립 파도를 일으켰다.

  • 그린베이에서 진행 중인 예인선 알버트가 웨이크업을 만들고 있다.

  • 국제우주정거장, 2006년에 열린 국제우주정거장에서의 오버라이크 방식의 보트 레이스.

  • 존 하바드 베이츠(미국 대통령) : "선박의 설계와 건설, Vol. II: 선박의 안정성, 저항성, 추진성 및 진동"(1908)

  • 선외기 모터가 있는 빠르고 작은 모터보트에서 깨어나십시오.

  • 웨이크 시뮬레이션

  • 켈빈 웨이크 시뮬레이션

  • 바지선 웨이크 비디오

  • 대형 모터보트 뒤에서 깨우기

기타 효과

위의 내용은 신체의 추진수단이 물에 다른 영향을 미치지 않는 이상적인 경풍을 설명한다. 실제로 V자 모양의 웨이브프론트 사이의 웨이브 패턴은 보통 프로펠러 역류 효과와 보트의 선미(일반적으로 사각 끝) 뒤에서 에딩하는 효과와 혼합된다.

켈빈 각은 또한 깊이의 함수로서 액이 다른 속도나 방향으로 흐르지 않는 깊은 물의 경우에 대해 유도된다("모양"). 물(또는 유체)이 수직인 경우에는 결과가 더 복잡할 수 있다.[5]

레크리에이션

"휴식 금지 구역"은 다른 보트에 의한 휴양을 촉진하고 손상의 취침 원인을 줄이기 위해 마리나, 계류장 근처 및 해안에서[6] 어느 정도 떨어진 곳에서 일어나는 것을 금지할 수 있다. 영국 운하에 동력을 공급받는 좁은 보트는, 둑을 따라 부서지는 세차(파열 파동을 일으킬 수 있을 만큼 큰 웨이크)를 하는 것이 허용되지 않는데, 이는 그들을 침식시키기 때문이다. 이 규칙은 일반적으로 이러한 선박을 4노트(4.6mph; 7.4km/h) 이하로 제한한다.

깨는 것은 때때로 오락적으로 사용된다. 수영하는 사람, 개인 수상기를 타는 사람, 돌고래와 같은 수중 포유류들은 경계의 선두에 설 수 있다. 웨이크보드를 타는 스포츠에서 웨이크는 점프로 사용된다. 웨이크서핑은 또한 웨이크서핑 스포츠에서 서퍼를 추진하는데 사용된다. 수구 종목에서는 드리블(dribbling)이라고 알려진 기술인 크롤 스트로크(crawling)에서 팔 스트로크가 번갈아 만들어지는 웨이크(wake)로 전진하면서 볼 캐리어가 헤엄칠 수 있다.

이미지 갤러리

  • 독일의 유일한 일관된 파도타기 지점은 배에서 거대한 웨이크업이다.

  • 17번가 다리를 바라보며 인도강변의 고속 모터 요트에서 깨어난다.

  • 발트해 페리 뒤에서 깨우기

  • 하와이 제도에서 보트 깨우기

  • 캐나다 브리티시 컬럼비아 근교에서 페리 보트가 발견됨.

참고 항목

참조

  1. ^ William Thomson (1887) "선박 파동," Institute of Mechanical Engineers, Procedures, 38 : 409–34; 삽화, 페이지 641–49.
  2. ^ 일시적인 켈빈 깨우기에 상응하는 이론은 마랑고니에 대해 더욱 파생되었다.촉, Jian-Jun(2004년)."과도 마란 고니 파도 물에 잠긴 몸의 충동적인 운동으로 인해".국제 응용 역학. 40(6):709–14. arXiv:1402.4474.Bibcode:2004년IAM....40..709S. doi:10.1023/B:INAM.0000041400.70961.1b.30003915.)과free-surface(촉, Jian-Jun(2006년)S2CID."일시적인 free-surface는 파도와 물에 잠겨 있는 소스의 충동적인 운동으로 인해".수중 기술 26일(4):133–37. arXiv:1402.4387. doi:10.3723/175605406782725023.S2CID 118527101.)을 이루고 있다.
  3. ^ 배의 "Hull Froude number"(Fr)는 Fr = U / √gL로 여기서 U는 선박의 속도, g는 지구 표면의 중력 가속도, L은 선박의 선체 길이, 즉 특징적인 파장이다. Marc Rabaud 및 Frédéric Moisy(2013) "선박 깨우기: 켈빈 또는 마하 각도?" 물리적 검토 편지, 110(21) : 214503을 참조하십시오. 온라인 이용 가능: 파리 대학교, 수드 대학교, 알렉산드르 다르몬, 마이클 벤자켄 및 엘리 라파엘(2014) "대형 프라우드 번호에서의 켈빈 웨이크 패턴," 저널 오브 플루이드 메카닉스, 738 : R3-1–R3-8. 온라인 이용 가능: ESPCI 파리 대학교테크
  4. ^ G.B. 휘담(1974년). 선형 및 비선형 파동(John Wiley & Sons Inc., 1974년) 페이지 409–10 온라인 스캔
  5. ^ 노르웨이 과학기술 대학, "2019년 8월 21일, "127년 묵은 물리 수수께끼 풀렸다". 2019년 8월 22일 회수
  6. ^ BoatWakes.org, 거리 표

외부 링크