잘린 롬비큐옥타헤드론

잘린 롬비큐옥타헤드론

슐레플리 기호	trr{4,3} = $tr{\begin{Bmatrix}4\\3\end{Bmatrix}}$ $tr{\begin{Bmatrix}4\\3\end{Bmatrix}}$ { $tr{\begin{Bmatrix}4\\3\end{Bmatrix}}$ $tr{\begin{Bmatrix}4\\3\end{Bmatrix}}$ $tr{\begin{Bmatrix}4\\3\end{Bmatrix}}$ ${\$
콘웨이 표기법	taaC
얼굴	50: 24 {4} 8 {6} 6+12 {8}
가장자리	144
정점	96
대칭군	O_h, [4,3], (*432) 주문 48
회전군	O, [4,3],⁺ (432), 주문 24
이중 다면체	디디아키스 이코시테트라헤드론
특성.	볼록한 조노헤드론

잘린 롬비큐옥타헤드론은 다면체로, 롬비큐옥타헤드론의 잘린 형태로 만들어졌다.옥타곤 18개, 육각 8개, 정사각형 24개로 구성된 50개의 얼굴을 가지고 있다.잘린 정육면체, 잘린 사면체, 삼각 프리즘으로 공간을 채울 수 있다.

기타 이름

잘린 작은 롬비큐옥타헤드론
베이딩 큐옥타헤드론

조노헤드론

조노헤드론으로서 12옥타곤을 제외한 모든 옥타곤을 일반 폴리곤으로 시공할 수 있다.그것은 그것의 중심에서 두 거리에 존재하는 48 정점 두 세트를 가지고 있다.

그것은 정육면체, 잘린 팔면체, 그리고 심방 도면체의 민코스키 합을 나타낸다.

잘린 롬비쿠옥타헤드론 발굴

잘린 롬비쿠옥타헤드론 발굴
얼굴	148: 8 {3} 24+96+6 {4} 8 {6} 6 {8}
가장자리	312
정점	144
오일러 특성	-20
속	11
대칭군	O_h, [4,3], (*432) 주문 48

출토된 잘린 롬비큐옥타헤드론은 12개의 불규칙한 팔각면을 제거한 잘린 롬비큐옥타헤드론에서 만들어진 토로이드 다면체다.그것은 6개의 사각 큐폴레, 8개의 삼각 큐폴레, 24개의 삼각 프리즘으로 구성되어 있다.^[1] 면 148개(삼각형 8개, 정사각형 126개, 육각형 8개, 옥타곤 6개), 가장자리 312개, 정점 144개를 가지고 있다.오일러 특성 χ = f + v - e = -20인 경우, 그 속(g = (2-14)/2)은 11이다.

삼각형의 프리즘이 없으면, 토로이드 다면체는 잘린 사각형이 된다.

발굴됨
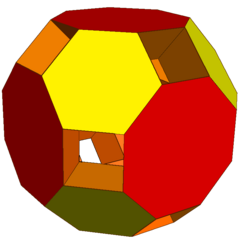잘린 롬비큐옥타헤드론	잘린 큐옥타헤드론

관련 다면체

잘린 큐옥타헤드론은 모든 정규 면과 4.6.8 꼭지점 형상이 유사하다.

롬비큐옥타헤드론의 삼각형과 사각형은 독립적으로 수정하거나 잘라서 다면체의 네 가지 순열을 만들 수 있다.부분적으로 잘린 형태는 잘린 형태의 가장자리 수축으로 볼 수 있다.

잘린 심비촉각체는 큐옥타헤드론에서 정류 및 절단 작업의 순서로 볼 수 있다.한 단계 더 교대하면 스너브 롬비쿠보옥타헤드론(snub rhombicuboctaheadron.

관련 다면체
이름	r{4,3}	rr{4,3}	tr{4,3}	수정됨 rrr{4,3}	부분적으로 잘림		잘림 trr{4,3}	srCO
콘웨이	AC	aaC=eC	taC=bC	aaaC=eaC	dXC	dXdC	taaC=baC	SAC
이미지
VertFiges	3.4.3.4	3.4.4.4	4.6.8	4.4.4.4 및_d 3.4.4_d.4	4.4.4.6 및_i 4.6.6_i	4.6.8_i 및 3.4.6_i.4	4.8.8 및_p 4.6.8_p	3.3.3.3.4 및 3.3.4.3.4