
구부러진 상태에서 두꺼운 종이책의 중간 면에 수직인 선의 방향. 티모셴코-에렌페스트 빔 이론은 20세기 초 스티븐 티모셴코와 폴 에렌페스트에[1][2][3] 의해 개발되었다.[4][5]모델은 전단 변형과 회전 휨 효과를 고려하여 파장이 빔의 두께에 접근할 때 고주파수 흥분 대상인 두꺼운 빔, 샌드위치 합성 빔 또는 빔의 거동을 설명하기에 적합하다.결과 방정식은 4차이지만 오일러-베르누엘리 빔 이론과 달리 2차 부분파생성 이론도 존재한다.물리적으로, 추가된 변형 메커니즘을 고려할 때, 그 결과는 정적 하중 하에서 더 큰 편향과 주어진 경계 조건 집합에 대한 더 낮은 예측 고유 빈도가 되는 반면, 빔의 강성을 효과적으로 감소시킨다.후자의 효과는 파장이 짧아질수록(원론적으로 빔 높이 또는 더 짧아질수록) 높은 주파수의 경우 더 눈에 띄며, 따라서 대립되는 전단력 사이의 거리가 감소한다.
로터리 관성 효과는 브레스와[6] 레일리가 도입했다.[7]
빔 재료의 전단 계수가 무한대에 접근하여 빔이 전단면에서 강성이 되고 회전 관성 효과가 무시되면 티모셴코 빔 이론은 일반적인 빔 이론으로 수렴된다.
콰지스타틱 티모셴코 빔

오일러-베르누엘리 빔(빨간색)과 비교하여 티모셴코 빔(파란색)의 변형. 
티모셴코 빔의 변형.정상 회전량은 /d x x}=\이며 d / d 과(와) 같지 않다
/ d 과(와) 같지 않다
축방향 효과가 없는 정적 티모셴코 빔 이론에서 빔의 변위는 다음과 같이 가정한다.

여기서( , , z은 빔의 점의 좌표, x , , u , u {는
빔의 점의 좌표, x , , u , u {는 3좌표 방향의 변위 벡터의 구성 요소
3좌표 방향의 변위 벡터의 구성 요소 , nmbea.am 및 은(는) -방향에서
, nmbea.am 및 은(는) -방향에서 중간 변위를 나타낸다
중간 변위를 나타낸다 .
.
지배 방정식은 다음과 같은 일반 미분 방정식의 결합 시스템이다.

정적 케이스에 대한 티모셴코 빔 이론은 위의 마지막 용어를 무시했을 때 오일러-베르누엘리 이론에 해당하며, 이 근사치는 다음에 유효하다.

어디에
- 은
 (는) 빔의 길이입니다.
(는) 빔의 길이입니다. - 은
 (는) 단면 영역이다.
(는) 단면 영역이다. - 은
 탄성계수다.
탄성계수다. - 은
 전단 계수다.
전단 계수다. - 은
 (는) 두 번째 영역이다.
(는) 두 번째 영역이다. - Timoshenko 전단 계수라고 불리는
 은 기하학에 따라 달라진다.일반적으로 직사각형 섹션의
은 기하학에 따라 달라진다.일반적으로 직사각형 섹션의  = /
= / - ( ) 은 분산 하중(길이당 힘)이다
 .
.
두 방정식을 조합하면, 일정한 단면의 동질 빔에 대해,

빔의 벤딩 모멘트 과
벤딩 모멘트 과 (와의 x {\ Q_은는) 와 관련이
(와의 x {\ Q_은는) 와 관련이 있으며, 회전 {\
있으며, 회전 {\ 선형 탄성 Timoshenko 빔의 경우 이러한 관계는 다음과 같다.
선형 탄성 Timoshenko 빔의 경우 이러한 관계는 다음과 같다.

| quasistic Timoshenko 보 방정식의 도출 |
Timoshenko 빔에 대한 운동학적 가정으로부터, 빔의 변위는 다음에 의해 주어진다.
그렇다면, 작은 변종들에 대한 변종-변종 관계로부터, 티모셴코 가정에 근거한 0이 아닌 변종들은 다음과 같다. 
빔의 실제 전단 변형률은 단면 전체에 걸쳐 일정하지 않기 때문에 다음과 같은 보정 계수 을(를) 도입한다. 보정 계수 을(를) 도입한다. 
빔의 내부 에너지 변화는 ![{\displaystyle \delta U=\int _{L}\int _{A}(\sigma _{xx}\delta \varepsilon _{xx}+2\sigma _{xz}\delta \varepsilon _{xz})~\mathrm {d} A~\mathrm {d} L=\int _{L}\int _{A}\left[-z~\sigma _{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+\sigma _{xz}~\kappa \left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} A~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8538120f720cdf9758cf966457cc594ab501443)
정의 
그러면 ![{\displaystyle \delta U=\int _{L}\left[-M_{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+Q_{x}\left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c36737b1d63a52a76cf0d34f07d97b340ccd61cb)
부품별 통합 및 경계 조건 때문에 빔의 끝에서 변동이 0이 된다는 점에 유의 ![{\displaystyle \delta U=\int _{L}\left[\left({\frac {\partial M_{xx}}{\partial x}}-Q_{x}\right)~\delta \varphi -{\frac {\partial Q_{x}}{\partial x}}~\delta w\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f25d6c444400ea89df8677e062734fb86236ac)
단위 길이당 가로 하중 , t) 에 의한 빔의 외부 작업 변동은 다음과 같다. 가로 하중 , t) 에 의한 빔의 외부 작업 변동은 다음과 같다. 
그렇다면 quasistic 빔의 경우 가상 작업의 원리는 다음과 같다. ![\delta U = \delta W \implies
\int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \left(\frac{\partial Q_{x}}{\partial x} + q\right)~\delta w\right]~\mathrm{d}L = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/d70338b0e41cd72e9b72cfa2dba0e4e4329467ee)
빔에 대한 지배 방정식은, 변이 미적분학의 기본 정리로부터, 
선형 탄성 빔의 경우 
따라서 빔에 대한 지배 방정식은 다음과 같이 표현될 수 있다. ![\begin{align}
\frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) + \kappa AG~\left(\frac{\partial w}{\partial x}-\varphi\right) & = 0 \\
\frac{\partial }{\partial x}\left[\kappa AG\left(\frac{\partial w}{\partial x} - \varphi\right)\right] + q & = 0
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1694f92bbda646acb7cbfca5f0497ff4165cac)
두 방정식을 함께 결합하면 
|
경계 조건
티모셴코 빔의 변형을 설명하는 2개의 방정식을 해결하려면 경계조건으로 증강해야 한다.문제가 잘 해결되려면 네 가지 경계 조건이 필요하다.대표적인 경계조건은 다음과 같다.
- 단순하게 지원되는 빔:두 지지대의 위치에서 의 변위는 0이다
 .빔에 적용되는
.빔에 적용되는 벤딩 모멘트 도 지정해야 한다.회전 과
벤딩 모멘트 도 지정해야 한다.회전 과 가로 전단력 Q 은 지정되지
가로 전단력 Q 은 지정되지 않았다.
않았다. - 클램프로 고정된 빔:고정된 끝에서 변위 및
 회전 }은는) 0으로 지정된다
회전 }은는) 0으로 지정된다 .한쪽 끝이 자유롭다면 그 에서 x 스타일 Q_와
.한쪽 끝이 자유롭다면 그 에서 x 스타일 Q_와 모멘트 M x 스타일 을 지정해야 한다
모멘트 M x 스타일 을 지정해야 한다 .
.
티모셴코 빔의 변형 에너지
티모셴코 빔의 변형 에너지는 휨과 전단력에 의한 변형 에너지의 합으로 표현된다.이 두 성분은 모두 변수에서 이차적이다.Timoshenko 빔의 변형 에너지 함수는 다음과 같이 기록할 수 있다.
![{\displaystyle W=\int _{[0,L]}{\frac {EI}{2}}\left({\frac {d\varphi }{ds}}\right)^{2}+{\frac {kGA}{2}}\left(\varphi -{\frac {dw}{ds}}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17ca330cbe6c7b25e8c4ad0c002de8ab2a19745)
예제: 캔틸레버 빔

자유단부의 점하중 하중을 받는 캔틸레버 티모셴코 빔 캔틸레버 빔의 경우, 한 경계는 클램핑되고 다른 경계는 자유롭다. 방향이 오른쪽으로 이고 z{\z} 방향이
오른쪽으로 이고 z{\z} 방향이 위로 양수되는 오른쪽 좌표계를 사용합시다.일반적인 관례에 따라, 긍정적인 힘은 및
위로 양수되는 오른쪽 좌표계를 사용합시다.일반적인 관례에 따라, 긍정적인 힘은 및  축의 긍정적인
축의 긍정적인 방향으로 작용하고 긍정적인 순간은 시계 방향으로 작용한다고 가정한다.또한 스트레스 결과물( 및
방향으로 작용하고 긍정적인 순간은 시계 방향으로 작용한다고 가정한다.또한 스트레스 결과물( 및
 의 기호 규약이 양수 휨모멘트가 빔의 하단에 있는 물질( z z좌표
의 기호 규약이 양수 휨모멘트가 빔의 하단에 있는 물질( z z좌표 )을 압축하고 양의 전단력이 빔을 시계 반대 방향으로 회전시키는 것으로 가정한다.방향의
)을 압축하고 양의 전단력이 빔을 시계 반대 방향으로 회전시키는 것으로 가정한다.방향의
클램핑된 끝은 = 이고 자유 은 0 이라고 가정해 봅시다
자유 은 0 이라고 가정해 봅시다 점 P{\ 을(를) 양의 z 방향으로
점 P{\ 을(를) 양의 z 방향으로 자유 끝에 적용하면
자유 끝에 적용하면 빔의 자유 본체 다이어그램이 제공됨
빔의 자유 본체 다이어그램이 제공됨

그리고

그러므로 휨모멘트와 전단력에 대한 표현으로부터 우리는

번째 방정식의 통합과 조건{= 0 {\을(를) = 에 적용하면 다음과 같은 결과를 얻을 수 있다
적용하면 다음과 같은 결과를 얻을 수 있다

두 번째 방정식은 다음과 같이 쓸 수 있다.

 = x=L에서 w = 0 {\이(가 제공하는
= x=L에서 w = 0 {\이(가 제공하는 경계 조건의 통합 및 적용
경계 조건의 통합 및 적용

축응력은 다음과 같이 주어진다.

다이나믹 티모셴코 빔
축방향 효과가 없는 티모셴코 빔 이론에서 빔의 변위는 다음과 같이 가정한다.

여기서( , , z은 빔의 점의 좌표, x , , u , u {는
빔의 점의 좌표, x , , u , u {는 3좌표 방향의 변위 벡터의 구성 요소
3좌표 방향의 변위 벡터의 구성 요소 , nmbea.am 및 은(는) -방향에서
, nmbea.am 및 은(는) -방향에서 중간 변위를 나타낸다
중간 변위를 나타낸다 .
.
위의 가정으로부터 시작하여 진동을 허용하는 티모셴코 빔 이론은 결합된 선형 부분 미분 방정식으로 설명할 수 있다.[8]
![\rho A\frac{\partial^{2}w}{\partial t^{2}} - q(x,t) = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ae3e2d14c1b5e59f0e4cd53c7a506b7d1111f8)

여기서 종속 변수는 ( x, )  의 변환 변위 및 ( ,t ) {\t)}, 각도 변위
의 변환 변위 및 ( ,t ) {\t)}, 각도 변위 오일러-베르누이 이론과 달리 각도 편향은 또 다른 변수로서 편향 기울기에 의해 근사치되지 않는다는 점에 유의한다.또,
오일러-베르누이 이론과 달리 각도 편향은 또 다른 변수로서 편향 기울기에 의해 근사치되지 않는다는 점에 유의한다.또,
- 은(는) 빔 재료의 밀도(선형 밀도는 아님)이다
 .
. - 은
 (는) 단면 영역이다.
(는) 단면 영역이다. - 은
 탄성계수다.
탄성계수다. - 은
 전단 계수다.
전단 계수다. - 은
 (는) 두 번째 영역이다.
(는) 두 번째 영역이다. - Timoshenko 전단 계수라고 불리는
 은 기하학에 따라 달라진다.일반적으로 직사각형 섹션의
은 기하학에 따라 달라진다.일반적으로 직사각형 섹션의  = /
= / - ( , t) 은 분산 하중(길이당 힘)이다
 .
. 

이러한 모수가 반드시 상수는 아니다.
선형 탄성, 등방성, 균일한 상수 단면 빔의 경우 이 두 방정식을 조합하여[9][10]

| 복합 Timoshenko 빔 방정식 |
일정한 단면의 동질 티모셴코 빔의 휨을 지배하는 방정식은 다음과 같다.
방정식 (1)부터 적절한 평활도를 가정하면 다음과 같다. 
차별화 방정식(2)이 
등식(3), 등식(4), 등식(5)을 등식(6)으로 대체하고 재배열하면 우리는 다음과 같은 결과를 얻게 된다. 
|
티모셴코 방정식은 임계 주파수 C= 2 = G I {\ I 정상 모드의 경우 티모드에서는 티모드 티모드 티모드 티모드 티모센코 방정식을 해결할 수 있다.4차 방정식인 , c {\{c 이하 주파수에 대해 2개의 진동 및 2개의 발생이
티모드에서는 티모드 티모드 티모드 티모드 티모센코 방정식을 해결할 수 있다.4차 방정식인 , c {\{c 이하 주파수에 대해 2개의 진동 및 2개의 발생이 .f {\c}}보다 큰 주파수의 경우 모든
.f {\c}}보다 큰 주파수의 경우 모든 용액은 진동이며, 결과적으로 두 번째 스펙트럼이 나타난다.[11]
용액은 진동이며, 결과적으로 두 번째 스펙트럼이 나타난다.[11]
축 효과
빔의 변위가 다음과 같은 경우

여기서 0 는 방향의 추가 변위이며
추가 변위이며 , 그러면 Timoshenko 빔의 지배 방정식이 형식을 취한다.
, 그러면 Timoshenko 빔의 지배 방정식이 형식을 취한다.
![\begin{align}
m \frac{\partial^{2}w}{\partial t^{2}} & = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t) \\
J \frac{\partial^{2}\varphi}{\partial t^{2}} & = N(x,t)~\frac{\partial w}{\partial x} + \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right)
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c35d8e346f27ef78d0a9c29ac3449ed4fb94b21)
여기서 = I J 및  (x , t) 은 외부에서
(x , t) 은 외부에서 가해지는 축력이다.외부 축력은 응력 결과에 의해 균형을 이룬다.
가해지는 축력이다.외부 축력은 응력 결과에 의해 균형을 이룬다.

여기서 는 축응력이며 빔의 두께는 으로 가정되었다
축응력이며 빔의 두께는 으로 가정되었다
축력 효과가 포함된 결합된 빔 방정식은 다음과 같다.

댐핑
축력 이외에 형태에 따른 속도에 비례하는 감쇠력을 가정할 경우

티모셴코 빔의 결합 방정식이 형태를 띠다.
![m \frac{\partial^{2}w}{\partial t^{2}} + \eta(x)~\cfrac{\partial w}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72225eea89af02d344a6877126ab80e276b33c9)

그리고 결합 방정식은

이 Ansatz 댐핑 힘(보강 점성)에 대한 주의사항은 점성이 빔 진동의 주파수 의존적이고 진폭에 독립적인 댐핑 속도를 유발하는 반면 경험적으로 측정한 댐핑 속도는 주파수 민감도가 낮지만 빔 편향 진폭에 따라 달라지는 것이다.
전단 계수
전단 계수를 결정하는 것은 간단하지 않다(결정된 값도 널리 수용되지 않는다, 즉 둘 이상의 답이 있다). 일반적으로 다음을 충족해야 한다.
- = G ( - )

전단 계수는 포아송의 비율에 따라 달라진다.정확한 표현을 제공하려는 시도는 스티븐 티모셴코,[12] 레이몬드 D를 포함한 많은 과학자들에 의해 이루어졌다. 민들린,[13] G. R. Cowper,[14] N. G. Stephen,[15] J. R.허친슨[16] 등 (Khanh C의 저서에서 변이성-아세트성 방법에 기초한 정제된 빔 이론으로서 티모셴코 빔 이론의 파생도 참조한다.정적[17] 케이스와 동적 케이스에서 서로 다른 전단 계수를 유도한다.)공학적 실무에서 스테판 티모셴코의[18] 표현은 대부분의 경우 충분하다.1975년 카네코는[19] 전단계수에 대한 연구에 대한 훌륭한 리뷰를 발표하였다.보다 최근 새로운 실험 데이터는 전단 계수가 과소평가된 것을 보여준다.[20][21]
Cowper - 선택에 따른 등방성 보의 교정 전단 계수.
| 단면 | 계수 |
 |  |
 |  |
 |  |
 |  |
 |  , where , where  |
 |  |
 |  |
 |  , where 1}:{}} 및 , where 1}:{}} 및 n= b n n= b n |
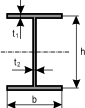 |  , where = m1}:{1}} 및 , where = m1}:{1}} 및 n= n{ n= n{ |
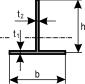 |  서m = t t {\ m1}:{1}:{1}} 및 서m = t t {\ m1}:{1}:{1}} 및 n= h n n= h n |
여기서 은(는) 포아송의 비율이다 .
.
참고 항목
참조
- ^ 아이작 엘리사코프, 2020년이른바 티모셴코 빔 이론을 누가 발전시켰는가?고체의 수학과 역학, 25(1) 97–116.https://doi.org/10.1177/1081286519856931
- ^ 엘리사코프, I,2020, Timoshenko-Ehrenfest Beam and Uflyand-Mindlin Plate Irons on Timoshenko-Ehrenfest Beam and Uflyand-Mindlin Plate 이론, World Scientific, 싱가포르, ISBN978-981-3236-51-6
- ^ 그리골류크, E.I., 2002, S.P. 티모셴코: 삶과 운명, 모스크바:항공 연구소 프레스(러시아어)
- ^ Timoshenko, S. P., 1921년, 철학잡지, 744페이지의 균일한 단면봉의 횡진동에 대한 미분방정식의 전단 보정계수에 대하여.
- ^ Timoshenko, S. P., 1922. 균일한 단면들의 막대들의 횡방향 진동들에 대하여, 철학적 잡지 125페이지.
- ^ 브레스 J.A.C., 1859년, Cours de mécanique applquée – Résistance des matériaux et stabilité des construction, 파리, Gautier-Villars(프랑스어)
- ^ Rayley Lord (J. W. S. Strutt), 1877-1878, Theory of Sound, London: Macmillan (Dover, New York, 1945 참조)
- ^ 티모셴코의 빔 방정식
- ^ Thomson, W. T., 1981년, 애플리케이션이 있는 진동 이론, 2판.프렌티스 홀, 뉴저지 주(州)
- ^ 로싱어, H. E.와 리치, I. G. 1977, 진동하는 등방성 빔의 전단 보정 J. Phys.D: Appl.물리, 10권, 페이지 1461-1466.
- ^ "티모셴코 빔 이론 예측에 대한 실험적 연구", A. 디아즈데안다, J. 플로레스, L. 구티레즈, R.A. 멩데즈 산체스, G. 몬시바스, A.Morales, Journal of Sound and Vibration, 제331권, 2012년 12월 17일, 페이지 5732–5744.
- ^ Timoshenko, Stephen P, 1932, Schwingungsprobleme der Technik, Julius Springer.
- ^ Mindlin, R. D., Deresiewicz, H., 1953년, Timoshenko의 보의 휨 진동에 대한 전단 계수, 기술 보고서 10번, ONR 프로젝트 NR064-388, 토목 공학부, 컬럼비아 대학교, 뉴욕 주 뉴욕 주.Y.
- ^ Cowper, G. R., 1966, "Timoshenko's Beam 이론에서의 전단 계수" J. Appl.메흐, 33권, 2권, 페이지 335–340.
- ^ Stephen, N. G., 1980."Timoshenko의 중력하중을 받는 빔으로부터의 전단계수", Journal of Applied Mechanics, 제47권, 제1호, 페이지 121–127.
- ^ Hutchinson, J. R., 1981년, "보의 교차 진동, 정확한 대 대략적인 해결책", Journal of Applied Mechanics, Vol. 48, No. 12, 페이지 923–928.
- ^ Le, Khanh C, 1999, 쉘과 봉의 진동, 스프링거.
- ^ Stephen Timoshenko, James M.이런, 재료의 역학.1972년 판 노스트랜드 라인홀드 주식회사 207쪽
- ^ 1975년 카네코, T. "Timoshenko's correction for shear in vibring beam," J. Phys.D: Appl.물리, 1927-1936 페이지 8.
- ^ "티모셴코 빔 이론의 정확성에 대한 실험적 점검", R. A. Méndes-Sachez, A. Morales, J. Flores, Journal of Sound and Vibration (2005) 508–512.
- ^ "임계주파수 이상의 티모셴코 빔 이론의 정확성에 대하여:베스트 전단 계수", J. A. Franco-Villafaigne 및 R. A. Méndes-Sanchez, Journal of Mechanics, 2016년 1월, 페이지 1–4. DOI: 10.1017/jmechanical.104.















 빔의 점의 좌표,
빔의 점의 좌표,  3좌표 방향의 변위 벡터의 구성 요소
3좌표 방향의 변위 벡터의 구성 요소




 (는) 빔의 길이입니다.
(는) 빔의 길이입니다. (는) 단면 영역이다.
(는) 단면 영역이다.

 (는)
(는) 




 (와
(와



![{\displaystyle \delta U=\int _{L}\int _{A}(\sigma _{xx}\delta \varepsilon _{xx}+2\sigma _{xz}\delta \varepsilon _{xz})~\mathrm {d} A~\mathrm {d} L=\int _{L}\int _{A}\left[-z~\sigma _{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+\sigma _{xz}~\kappa \left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} A~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8538120f720cdf9758cf966457cc594ab501443)

![{\displaystyle \delta U=\int _{L}\left[-M_{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+Q_{x}\left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c36737b1d63a52a76cf0d34f07d97b340ccd61cb)
![{\displaystyle \delta U=\int _{L}\left[\left({\frac {\partial M_{xx}}{\partial x}}-Q_{x}\right)~\delta \varphi -{\frac {\partial Q_{x}}{\partial x}}~\delta w\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f25d6c444400ea89df8677e062734fb86236ac)


![\delta U = \delta W \implies
\int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \left(\frac{\partial Q_{x}}{\partial x} + q\right)~\delta w\right]~\mathrm{d}L = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/d70338b0e41cd72e9b72cfa2dba0e4e4329467ee)


![\begin{align}
\frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) + \kappa AG~\left(\frac{\partial w}{\partial x}-\varphi\right) & = 0 \\
\frac{\partial }{\partial x}\left[\kappa AG\left(\frac{\partial w}{\partial x} - \varphi\right)\right] + q & = 0
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1694f92bbda646acb7cbfca5f0497ff4165cac)

![{\displaystyle W=\int _{[0,L]}{\frac {EI}{2}}\left({\frac {d\varphi }{ds}}\right)^{2}+{\frac {kGA}{2}}\left(\varphi -{\frac {dw}{ds}}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c17ca330cbe6c7b25e8c4ad0c002de8ab2a19745)


 자유
자유 




 적용하면 다음과 같은 결과를 얻을 수 있다
적용하면 다음과 같은 결과를 얻을 수 있다





![\rho A\frac{\partial^{2}w}{\partial t^{2}} - q(x,t) = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ae3e2d14c1b5e59f0e4cd53c7a506b7d1111f8)















![\begin{align}
m \frac{\partial^{2}w}{\partial t^{2}} & = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t) \\
J \frac{\partial^{2}\varphi}{\partial t^{2}} & = N(x,t)~\frac{\partial w}{\partial x} + \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right)
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c35d8e346f27ef78d0a9c29ac3449ed4fb94b21)



 축응력이며 빔의 두께는
축응력이며 빔의 두께는 


![m \frac{\partial^{2}w}{\partial t^{2}} + \eta(x)~\cfrac{\partial w}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72225eea89af02d344a6877126ab80e276b33c9)



















