반지름 속도

관찰자에 대한 목표물의 반경 속도 또는 시선 속도는 두 점 사이의 거리 또는 범위의 변화 속도이다.이는 두 점을 연결하는 상대 방향에 대한 목표-관측자 상대 속도의 벡터 투영과 동일합니다.천문학에서, 지점은 보통 지구상의 관찰자로 간주되기 때문에, 반경 속도는 물체가 지구로부터 멀어지는 속도를 나타냅니다(또는 음의 반경 속도로 접근).

공식화

주어진 미분 가능한 $벡터{\displaystyle \mathbf{}}$ r ${\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ 3${\displaystyle \mathbf${r}$\epsilon \mathbb${R}$^{3$}}은$$ 관찰자에 상대적인 대상의 순간 위치를 정의한다.

허락하다

${\displaystyle \mathbf {v} = specfrac {d\mathbf {r} } {dt}}$

(1)

$v$${\displaystyle }$$${\$displaystyle \mathbf {v}$${\$ {\$displaystyle \epsilon$} ${\displaystyle {}^{}}$ 3 {\$displaystyle \mathbb {R}$^{$3$을 $사용$하여 관찰자에 대한 목표물의 순간 속도입니다.

위치 $벡터{\displaystyle \mathbf{}}$r(\$displaystyle \mathbf {r})$의 크기는 다음과 같이 정의됩니다.

${\displaystyle r=\mathbf {r} \ =\displayle \mathbf {r} ,\mathbf {r} \rangle ^{1/2}}$

(2)

수량 범위 속도는 r$\$의 크기(표준)의 시간 미분입니다.다음은 다음과 같습니다.

${\displaystyle\frac{dr}{dt}}$

(3)

(2)를 (3)으로 대체하다

${\displaystyle\frac {dr}{dt}=paramfrac {d\mathbf {r},\mathbf {r} \rangle ^{1/2}}{dt}}}$

우측 도함수 평가

${\displaystyle {frac {dr} {dt} = frac {1} {2} } {\frac {dr} ,\mathbf {r} \rangle } {dt} {\frac {1} {r} }$

${\displaystyle {frac {dr} {dt} = frac {1} {2} {\frac {d\mathbf {r} {dt}}, \mathbf {r} +\frac \mathbf {r} {r}, {\frac {dr} {dr} } }$

(1)을 사용하면 이 표현은

${\displaystyle {frac {dr} {dt} = frac {1} {2} {\frac {v} , \mathbf {r} \rangle + \mathbf {r} , \mathbf {v} \rangle }$

그^[1] 이후

$\displaystyle \mathbf {v} ,\mathbf {r} \rangle =\displayle \mathbf {r} ,\mathbf {v} \rangle }$

와 함께

$(\displaystyle\hat\mathbf {r}}=blac(\mathbf {r}} {r})$

레인지 레이트는 다음과 같이 정의됩니다.

${\displaystyle\frac{dr}{dt}=mathbf{r},\mathbf {v}\rangle}=\mathbf {r},\mathbf {v}\rangle }$

r$^\$ $단위$ 벡터에 속도 벡터를 목표로 하는 관찰자의 투영.

r $=$ [ ${\displaystyle \begin{array}{c}0\mathrm{}\end{array}}$ ${\displaystyle \begin{array}{}0\\ \mathrm{}\end{array}}$ $]$ ${{displaystyle \mathbf${r} $={bmatrix} 0\\0\end${bmatrix$\}\}\}\}$과 같은 관측자 표적에 특이점이 존재한다. 이 경우 범위 속도는 r ${\displaystyle =}$ $({displaystyle$ r$=0$으로 $존재$하지 않는다.

천문학에서의 응용

천문학에서 방사 속도는 종종 도플러 분광법에 의해 근사치의 1차까지 측정된다.이 방법으로 얻을 수 있는 양은 중심 반지름 속도 측정 또는 분광 반지름 ^[2]속도라고 할 수 있다.그러나 빛이 천문학적 물체에서 관찰자에게 도달하기 위해 일반적으로 이동하는 먼 거리에 걸친 상대론적 효과와 우주론적 효과로 인해, 이 측정치는 물체와 ^[3]관찰자 사이의 공간에 대한 추가적인 가정 없이는 기하학적 반지름 속도로 정확하게 변환될 수 없습니다.반면, 측성 방사 속도는 측성 관측에 의해 결정된다(예: 연간 ^[3][4][5]시차의 장기적 변화).

분광 방사 속도

방출 시 상당한 상대 방사 속도를 가진 물체의 빛은 도플러 효과를 받기 때문에 멀어지는 물체는 빛의 빈도가 감소하고(빨간색 이동), 다가오는 물체는 증가한다(청색 교대).

별이나 다른 발광 거리 물체의 반경 속도는 고해상도 스펙트럼을 취하여 알려진 스펙트럼 라인의 측정된 파장과 실험실 측정의 파장을 비교함으로써 정확하게 측정할 수 있습니다.양의 반지름 속도는 물체 사이의 거리가 증가하고 있거나 증가하고 있음을 나타냅니다. 음의 반지름 속도는 선원과 관측자 사이의 거리가 감소하고 있거나 감소하고 있음을 나타냅니다.

윌리엄 허긴스는 1868년에 별의 빛의 ^[6]관측된 적색 편이를 바탕으로 태양에 대한 시리우스의 반지름 속도를 추정했습니다.

많은 쌍성에서 궤도 운동은 보통 초당 수 킬로미터의 반지름 속도 변화를 일으킵니다.도플러 효과로 인해 이러한 별들의 스펙트럼이 달라지기 때문에 분광 쌍성이라고 불립니다.반지름 속도는 별의 질량과 이심률, 반조르 축과 같은 일부 궤도 요소의 비율을 추정하는 데 사용할 수 있습니다.같은 방법으로 별 주위의 행성을 탐지하는 데에도 사용되었는데, 그 방법은 행성의 공전 주기를 결정하는 것이며, 그 결과 생긴 반지름-속도 진폭은 2진수 질량 함수를 사용하여 행성의 질량에 대한 하한을 계산할 수 있게 해준다.시선방향 속도법만으로 하한선을 알 수 있는데, 시선방향에 매우 높은 각도로 공전하는 큰 행성은 시선방향에 궤도면이 있는 훨씬 작은 행성만큼 반지름방향으로 별을 교란시킬 것이기 때문이다.이 방법으로 계산한 이심률이 높은 행성은 실제로는 원형 또는 원근원 공명 ^[7][8]궤도의 두 행성계일 수 있다는 주장이 제기되어 왔다.

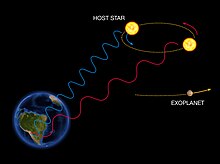
외계 행성 발견

외부행성을 탐지하는 지름속도법은 중심별의 속도 변화를 감지하는 데 기초하고 있는데, 이는 별 주위를 도는 (보이지 않는) 외부행성의 중력 방향이 바뀌기 때문입니다.별이 우리를 향해 움직일 때, 스펙트럼은 파란색으로 변하는 반면, 우리로부터 멀어질 때는 빨간색으로 바뀝니다.항성의 스펙트럼을 정기적으로 관찰하여 속도를 측정함으로써 항성이 외계행성 동반성의 영향으로 주기적으로 움직이는지 여부를 확인할 수 있습니다.

data 축소

계기적 관점에서 속도는 망원경의 움직임에 비례하여 측정됩니다.따라서 데이터 감소의 중요한 첫 번째 단계는 데이터 감소의 기여도를 제거하는 것입니다.

• 약 ± 30km/s의 속도로 태양 주위를 도는 지구의 타원 운동
• 지구-달 시스템의 ^[9]무게 중심을 중심으로 한 달의 지구 자전은 ± 13m/s이다.
• 적도에서 최대 ±460m/s이고 망원경의 지리적 위도의 코사인(cosine)에 비례하는 지구축을 중심으로 한 지구 지각과 함께 망원경의 일일 회전
• mm/s 수준에서 지구 극성 운동의 작은 기여,
• 은하 중심 주위의 움직임으로부터 230km/s의 기여도와 관련 고유 움직임.^[10]
• 스펙트럼 분석 측정의 경우 ^[11]수차와 관련하여 ±20cm/s의 순서로 보정한다.
• Sini 퇴행은 움직임의 평면에 있지 않기 때문에 발생하는 충격이다.

「 」를 참조해 주세요.

• 고유 운동 – 하늘의 별 겉보기 위치에서 관측된 변화를 측정합니다.
• 고유 속도 – 정지 프레임에 대한 물체의 속도
• 상대속도 – 다른 물체 또는 관찰자 A의 나머지 프레임에 있는 물체 또는 관찰자 B의 속도
• 우주 속도(천문)
• 쌍방향 레인지 레이트
• 도플러 효과
• 내부 제품
• 궤도 결정
• Lp 공간

레퍼런스

• 외계행성을 탐색하는 지름속도 방정식(도플러 분광법 또는 워블법)

추가 정보

• Hoffman, Kenneth M.; Kunzel, Ray (1971), Linear Algebra (Second ed.), Prentice-Hall Inc., ISBN 0135367972
• 렌제, 존, 스토버, 크리스토퍼, 웨이스틴, 에릭 W. "내부 제품"From Math World: 울프램 웹 리소스.http://mathworld.wolfram.com/InnerProduct.html