원통형 및 구형 좌표 분석

이것은 공통 곡선 좌표계로 작업하기 위한 일부 벡터 미적분 공식의 목록이다.

메모들

이 글은 구면 좌표(다른 출처가 θ과 φ의 정의를 뒤바꿀 수 있음)에 대해 ISO 31-11을 대체하는 표준 표기법 ISO 80000-2를 사용한다.
- 극각은 $\theta \in [0,\pi ]$ [ $\theta \in [0,\pi ]$ , $\theta \in [0,\pi ]$ $\theta \in [0,\pi ]$ $\theta \in [0,\pi ]$ : 원점에 연결하는 z축과 방사형 벡터 사이의 각이다.
- 방위각은 $\varphi \in [0,2\pi ]$ [ $\varphi \in [0,2\pi ]$ $\varphi \in [0,2\pi ]$ $\varphi \in [0,2\pi ]$ $\varphi \in [0,2\pi ]$ $[\displaystyle \varphi \in [0,2\pi ]}$ : x축과 xy-plane에 방사형 벡터의 투영 사이의 각이다.
atan2(y, x) 함수는 그 영역과 이미지 때문에 수학 함수 아크탄(y/x) 대신 사용할 수 있다. 고전적인 아크탄 함수는 (-π/2, +π/2)의 이미지를 갖는 반면, atan2는 (- (-, π)의 이미지를 갖는 것으로 정의된다.

좌표 변환

데카르트 좌표, 원통형 좌표 및 구형 좌표^[1] 간 변환

		보낸 사람
		카르테시안	원통형	구면
에게	카르테시안	해당 없음	${\displaysty}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\ended}}}$	${\displaysty}x&=r\sin \cos \varphi \\y&=r\sin \sin \varphi \\z&=r\cos \theta \ended}}}$
	원통형	${\displaysty}\rho &={\sqrt {x^{2}+y^{2}}}}\\\varphi &=\arctan \left({\frac {y}{x}\오른쪽)\z&=z\end}$	해당 없음	${\regated}\rho &=r\sin \theta \\\varphi &=\z&=r\coses \theta \ended{arged}}}$
	구면	${\displaysty}r&={\sqrt {x^{2}+y^{2}+z^{2}}}}\\\theta &=\arctan \left({\frac {\sqrt{x^{2}+y^{2}}}{z}\오른쪽)\\\varphi &=\arctan \leftfr\fractan {y}{x}\right)\end{aigned}}}$	${\displaysty}r&={\sqrt {\rho ^{2}+z^{2}}}}\\\theta &=\arctan {\reft({\fractan {\rho }{z}\오른쪽)}}\\\varphi &=\varphi \end{aigned}}$	해당 없음

단위 벡터 변환

데카르트^[1], 원통형 및 구형 좌표계의 단위 벡터 간 대상 좌표 변환

	카르테시안	원통형	구면
카르테시안	해당 없음	${\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}$	${\displaystyle{\begin{정렬}{\hat{\mathbf{)}}}&=\sin\theta\cos \varphi{\hat{\mathbf{r}}}+\cos\theta\cos \varphi{\hat{\boldsymbol{\theta}}}-\sin\varphi{\hat{\boldsymbol{\varphi}}}\\{\hat{\mathbf{y}}}&=\sin\theta\sin \varphi{\hat{\mathbf{r}}}+\cos\theta\sin \varphi{\hat{\boldsymbol{\theta}}}+\cos \varphi. {\hat{)굵은 심볼 {\barphi }}\\\\hat {\mathbf {z}}}}}}}\cos \theta {\mathbf {r}-\sin \\chat {\\hatsymbol {\}\theta }\end{aigned}}}}}}}}}}}}}}}}}}}}}}?$
원통형	${\signified}{\hatsymbol {\rho}}&={\frac {x{\x{\x}}}+y{\mathbf {y}}}}{\sqrt {x^{2}+y^{2}}}}}}\{\hat{\hatsymbol {\barphi }}}&={\frac {-y}{-y}}}+x{\mathbf {y}}}{\sqrt {x^{x^}+y^{2}}{\sqrt}}}}}}\{\hat{\mathbf{z}}}}}}}}}{\mathbf {z}}}$	해당 없음	${\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}$
구면	${\mathbf{r}}{}}}{}}}}{{\frac {x}}}{x{\x{\x{x}}}}}}}}}{\sqrt {x^{x^{x^{x^}+z^{x}{x}}}}}}}{xfr}}{xfr}}}}}}}}}}{xfrt}}}}}}{xfr^{xfline^{xf}}}}}}}}}}}}}}}\{\hat{\hatsymbol{\\theta}}}&={\frac {\\flac(x{\\\x}}}}}}}}}}}+y{\mathbf {}}}}}}}\z-\(x^{2}+y^{2}}}}\오른쪽){\hat {\mathbf {z}}{{\sqrt {x^{2}+y^{2}+z^{2}}{2}+z^{2}}}}{\sqrt {x^{2}+y^{2}}}}}\{\hat{\hatsymbol {\barphi }}}&={\frac {-y}{-y}}}+x{\mathbf {y}}}{\sqrt {x^{x^}+y^{2}}}}}}}\end{정렬}$	${\regated}{\hatsbf{r}}{}}}}{}}}{\mathbf {rhat {\rhatsymbol {\rho}}}}}{\sqrt {\rho ^{2}+z^{2}}}}}}}}\{\hat{\hat symbol{\theta}}}&={\frac {z{\hat{\\hatsymbol{\rho}}-}-\hat {\mathbf{z}}}}}}{\sqrt{\rho ^{2}}}}\{\hat{\hat}\\symbol {\varphi }}}}&={\hat {\\barphi }}\ended}}}}}$	해당 없음

선원 좌표계에 따른 데카르트, 원통형 및 구형 좌표계의 단위 벡터 간 변환

	카르테시안	원통형	구면
카르테시안	해당 없음	${\mathbf {x}}{}}}}{\frac {x{\x{\x{\hatsymbol{\rho}}}-y}-y}{\sqrt{x^{x^}+y^{2}}}}}}}}\{\mathbf{y}}}}}{\frac {y}}{\frac {\frhatsymbol {\rho }}}}+x{\notsymbol {\varphi}}}}}{\sqrt{x^{2}+y^{2}{2}}}}}}}}}}}}}}}}2}}}}\{\hat{\mathbf{z}}}}}}}}}{\mathbf {z}}}$	${\mathbf {x}}{\mathbf{x}}}}}}{\frac {x\left\sqrt {x^{2}+y^{2}{2}}}}{{\hatsbf{r}}}}}}}}}{}+z{{}}}+z^{\hat {\hatsymbol {\\the}}}\sqrt{x^{2}+y^{2}+z^{2}}}}}}}{{\hat{\\hatsymbol{\\varphi }}}}}{{\sqrt{x^{2}+y^{2}}}{2}}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\{\hat {\mathbf{y}}}}}}}}}}{\frac {y\left\sqrt{x^{2}+y^{2}}}{{\hat{\mathbf{r}}}}}}}}{}+z{\hat{\hat}}{\hatsymbol {\the}}}\xqrt{x^{2}+y^{2}+z^{2}}}}}}}{{\hat{\\hatsymbol{\\varphi }}}}}{{\sqrt{x^{2}+y^{2}}}{2}}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\{\hat {\mathbf{z}}}}}}}}{\frac {z{\mathbf {r}}}}}}-{\sqrt{x^{2}+y^{2}}}}}{{\hat {\chatsymbol {\theta}}}{\\sqrt {x^{2}+y^{2}+z^{2}}}}}}\end{정렬}$
원통형	${\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}$	해당 없음	${\required}{\hatsymbol {\rho }}&={\frac {\rhat {\\rhatbf{r}}}}+z{\hatsymbol {\ta}}}{\sqrt}+z^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{정렬}$
구면	${\displaystyle{\begin{정렬}{\hat{\mathbf{r}}}&=\sin\theta \left(\cos \varphi{\hat{\mathbf{x}}}+\sin \varphi{\hat{\mathbf{y}}}\right)+\cos({\hat{\mathbf{z}}}\\{\hat{\boldsymbol{\theta}}}&=\cos \left(\cos \varphi{\hat{\mathbf{x}}}+\sin \varphi{\hat{\mathbf{y}}}\right)-\sin \theta{\hat{\mathbf{z}\theta. }}\\{\hat{\\mathbf{x}}}\\sin \varphi {\varphi {}&=-\sin \varphi {\\mathbf {x}}}}}}+\cos \varphi {\mathbf {y}}}}}$	${\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}$	해당 없음

델 공식

데카르트, 원통형 및 구형 좌표계의 델 연산자가 있는 표

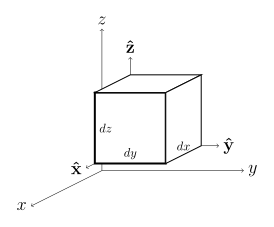
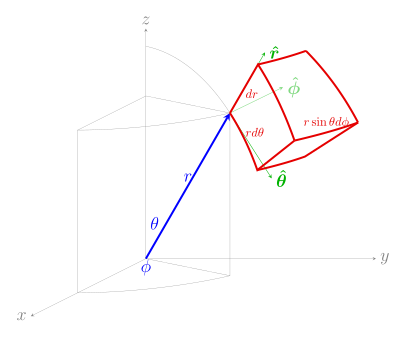
작전	데카르트 좌표, 평행 좌표. $(x, y, z)$	원통좌표 $(ρ, φ, z)$	구형좌표 $(r,$ $θ,$ $φ)$ 여기서 $θ$ 은 극각, $φ$ 은 방위각이다^α.
벡터장 $A$	$A_{x}{\hat {\mathbf {x}}}}}+A_{y}{\hat {\mathbf {y}}}}}+A_{z}{\hat {\mathbf {z}}}}$	$A_{\rho }{\hat {\boldsymbol {\rho }}+A_{\barphi }{\hat {\boldsymbol {\barphi }}+A_{z}{\hat {\mathbf {z}}}}}}$	$A_{r}{\hatsbf{r}}}}}}}}}}}}{}+A_{\theta}{\hat {\boldsymbol{\ta}}}+A_{\barphi }{\hat {\boldsymbol {\barphi }}}}$
그라데이션 $\nabla f$ ^[1]	${\mathbf {x}{\mathbf{x}}}}+{\mathbf {y}}+{\mathbf \}{\mathbf {}{}}}}}}}$	${\reason f \rho \cHot \rho \}{1\over \rho }{\reason f \varphi }}{\hat \\mathb{z}}}}}}}}{\cHat \mathb}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$	${\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}$
발산 $a$ ^[1]	${\partial A_{x} \partial x}+{\partial A_{y} \partial y}+{\partial A_{z} \partial z}} \partial z}$	${1 \rho }{\partial \left(\rho A_{\rho }\partial \partial \partho }+{\rho }{\rho }{\partial A_{z} \partial z}}}) 위에 \partial \partho$	${1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }$
컬 $\times \times A$ ^[1]	${\displaystyle{\begin{정렬}({\frac{\partial A_{z}}{\partial는 y}}-{\frac{\partial A_{y}}{\partial z}}\right)&,{\hat{\mathbf{)}}}\\+\left({\frac{\partial A_{x}}{\partial z}}-{\frac{\partial A_{z}}{\partial x}}\right)&,{\hat{\mathbf{y}}}\\+\left({\frac{\partial A_{y}}{\partial x}}-{\frac{\partial A_{x}}{\partial는 y}}\right)&am.p/&{\hat{\mathbf {z} }}\end{aigned}}$	${\displaystyle{\begin{정렬}({\frac{1}{\rho}}{{\partial A_{z}}{\partial \varphi}}\frac-{\frac{\partial A_{\varphi}}{\partial z}}\right)&,{\hat{\boldsymbol{\rho}}}\\+\left({\frac{\partial A_{\rho}}{\partial z}}-{\frac{\partial A_{z}}{\partial \rho}}\right)&,{\hat{\boldsymbol{\varphi}}}\\+{\frac{1}{\rho}}\left({\frac{.\partial \left(\rho A_{\varphi }}\오른쪽)}{\partial \rho }-{\partial A_{\rho }}{\partial \varphi }}}{\hat {\mathbf{z}}}}}}}}}}}}$	${\displaystyle{\begin{정렬}{\frac{1}{r\sin \theta}}\left({\frac{}\partial{\partial \theta}}\left(A_{\varphi}\sin\theta \right)-{\frac{\partial A_{\theta}}{\varphi\partial}}\right)&{\hat{\mathbf{r}}}\\{}+{\frac{1}{r}}\left({\frac{1}{\sin \theta}}{\frac{\partial A_{r}}{\varphi\partial}}-{\frac{\partial}{r\partial}}\left.(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
라플라스 연산자 $\nabla 2 f \equiv \equiv f f$ ^[1]	${\cHB^{2}f \over x^{2}}+{\\cHB^{2}f \over y^{2}f \cHB^{2}}}$	${\1 \rho }{\cHB\over \rho }\왼쪽(\rho }\ref)+{1 \rho \rho \}{2}}:{{2}}: \rho ^{2}f \varphi \{2}}:{{{{{{{{}f}f \f \f \f \varphaff}f \vaff}{{{nozzzzzz^{}}}}}}}}$	${1\over r^{2}}: \\\cHB \over r}\!\left(r^{2}){\back f \over \cHB r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\\\\\{\\\\\}{\\\\}{\\\\}}{\\\\\\\\\\\\}\left(\sin \sin \theta \\timef \over \theta }\right)\!+\!{1 \over r^{2}\\sin ^{2}\theta }{\notes ^{2}f \over \varphi ^{2}}$
벡터 라플라시안 $A 2 a \equiv \equiv a a a a$ ^[2]	$\nabla ^{2}A_{x}{\hatsbf {x}}}}:{2}A_{y}{\hat {\mathbf{y}}}}}}{2}A_{z}{\hattbf {z}}}}}$	${\mathopen {}{}\mathopen {}\좌측(\mathla ^{2}A_{\rho }-{\frac {A_{\rho }}{\rho ^{2}}}-{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\rho }}}\\+{\mathopen {}}\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{\rho ^{2}}}+{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\varphi }}}\\{}+\nabla ^{2}A_{z}&{\hat {\mathbf {z} }}\end{aligned}}$	${\displaysty}\왼쪽(\javla ^{2})A_{r}-{\frac {2A_{r}}{r^{2}}}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial \left(A_{\theta }\sin \theta \right)}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\+\left(\nabla ^{2}A_{\theta }-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}+{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}$
재료파생상품^α^[3] $(A \cdot \nabla) B$	$\mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}$	${\displaystyle{\begin{정렬}(A_{\rho}{\frac{\partial B_{\rho}}{\partial \rho}}와{\frac{A_{\varphi}}{\rho}}{\frac{\partial B_{\rho}}{\partial \varphi}}+A_{z}{\frac{\partial B_{\rho}}{\partial z}}-{\frac{A_{\varphi}B_{\varphi}}{\rho}}\right)&,{\hat{\boldsymbol{\rho}}}\\+\left(A_{\rho}{\frac{\partial B_{\varphi}}{\parti.알)화법}}+{\frac{A_{\varphi}}{\rho}}{\frac{\partial B_{\varphi}}{\varphi\partial}}+A_{z}{\frac{\partial B_{\varphi}}{z\partial}}+{\frac{A_{\varphi}B_{\rho}}{\rho}}\right)&{\hat{\boldsymbol{\varphi}}}\\+\left(A_{\rho}{\frac{\partial B_{z}}{\rho\partial}}+{\frac{A_{\varphi}}{\rho}}{\frac{\partial B_{z}}{\varphi\partial}}+A._{z}{\frac {\partial B_{z}}{\partial z}}\right)&#{\hat {\mathbf {z}}}\ended}}}$	${\displaystyle{\begin{정렬}(A_{r}{\frac{\partial B_{r}}{\partial r}}와{\frac{A_{\theta}}{r}}{\frac{\partial B_{r}}{\partial \theta}}와{\frac{A_{\varphi}}{r\sin \theta}}{\frac{\partial B_{r}}{\partial \varphi}}-{\frac{A_{\theta}B_{\theta}+A_{\varphi}B_{\varphi}}{r}}\right)&,{\hat{\mathbf{r}}}\\+\left(A_{r}{\frac{\partial.B_{\theta}}{r\partial}}+{\frac{A_{\theta}}{r}}{\frac{\partial B_{\theta}}{\theta\partial}}+{\frac{A_{\varphi}}{r\sin \theta}}{\frac{\partial B_{\theta}}{\varphi\partial}}+{\frac{A_{\theta}B_{r}}{r}}-{\frac{A_{\varphi}B_{\varphi}\cot \theta}{r}}\right)&{\hat{\boldsymbol{\theta}}}\\+\left(A_{r}{\frac{\partial B_{\varphi}}{년.부분ial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\varphi }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+{\frac {A_{\varphi }B_{r}}{r}}+{\frac {A_{\varphi }B_{\theta }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}$
텐서 ∇⋅ $T$ (2차 텐서 차이와 혼동하지 않음)	${\displaystyle{\begin{정렬}({\frac{T_{xx}}{\partial x}}와{\frac{\partial T_{yx}}{\partial는 y}}와{\frac{\partial T_{zx}}{\partial z}}\right\partial)&,{\hat{\mathbf{)}}}\\+\left({\frac{\partial T_{xy}}{\partial x}}와{\frac{\partial T_{yy}}{\partial는 y}}와{\frac{\partial T_{zy}}{\partial z}}\right)&,{\hat{\mathbf{y}}}\\+\left({\f.rac{\partial T_{xz}}{\partial x}}{\frac {\partial T_{yz}}{\partial y}}{\partial T_{z}}}}}{partial z}\right)&{\hat {\mathbf{z}}}}}}}}$	${\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf{z}}}\end{aigned}$	${\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \{{\partial T_{\varphi r}}}{\partial \varphi }}{{\partial \varphi }}}}{{\partifial \varphi{1}{1}{{{r}}}\ta \varpha]{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta \}+{\frac {1}{r\sin \}}}}{{\frac {\partial T_{\varphi \}}}}}{{\partial \varphi }}}}{r}-{\fr-{\frac {\cot }{r}}}}}}}}}}}}}}}}}}}}}T_{\barphi \varphi \}\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta }\right]&{\hat {\\hatsymbol {\varphi }}\ended{aigned}}$
차동변위 $dℓ$ ^[1]	$dx\,{\hat {\mathbf {x}}}}}:{\hat {\mathbf {x}}}}, {\mathbf {y}}}}, {\hatsbf {z}}}}$	$d\rho \,{\hatsymbol {\rho }}+\rho \,d\varphi \,{\\hatsymbol {}}+dz\,{\hat {\mathbf {z}}}}}}}}}}}}}}}$	$dr\,{\hatsbf {r}}}}}}}}}}}}{\mathbf {r},d\d\varphi \}}}}},\sin \theta \,d\varphi \}}}}}}}}}}}}}}}"$
차동 정상 영역 $dS$	${\displaystyle {\mathbf {x}\}\}\{}+dx\,dz&\}\\\\\\\\mathbf {y}\}\}}}}}\mathbf {z}}}}{\mathbf {}}}}}}}\mathbf {}}}}}{jand{nd}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{$	${\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}$	${\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}$
차동 볼륨 $dV$ ^[1]	$dx\,dy\,dz}$	$\rho \,d\rho \,d\varphi \,dz$	$r^{2}\sin \theta \,dr\,dr\theta \,d\varphi$

^α 이 페이지는 극각에는

\theta

{\displaystyle

\

theta }

을(를) 사용하고

\varphi

,

\varphi

에는

display

{\

displaystyle

\varphi }을

(

를) 사용하며, 물리학에서 흔히 볼 수 있는 표기법이다. 이러한 공식에 사용되는 소스는 방위각의 경우

\theta

\varphi

\theta

을(를) 사용하고, 극각의 경우

\varphi

{

\varphi

{\

displaystyle \varphi

}을(를) 사용하며, 이는 일반적인 수학 표기법이다. 수학 공식을 얻으려면 위의 표에 표시된 공식에서

\varphi

\theta

\theta

\varphi

{

\varphi

{\

displaystyle \varphi

}을(를) 전환하십시오.

비교 계산 규칙

$\div} \,\divname {grad} f\equiv \cdla \cdot \cdla f\equiv \equla ^{2}f$
$\chostname {grad} f\\equiv \equiv \chavla \p=\mathbf {0$
$\operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot(\nabla \times \mathbf {A} )=0$
$\operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A}$ (Lagrange's formula for del)
$\bla ^{2}(fg)=f\bla ^{2}g+2\bla f\cdot \bla g+g\bla ^{2}f$

데카르트 파생

${\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)\,dy\,dz-A_{x}(x)\,dy\,dz+A_{y}(y+dy)\,dx\,dz-A_{y}(y)\,dx\,dz+A_{z}(z+dz)\,dx\,dy-A_{z}(z)\,dx\,dy}{dx\,dy\,dz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}$

${\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)\,dz-A_{z}(y)\,dz+A_{{y}(z)\,dy-A_{y}(z+dz)\,dy}{dy\,dz}\\\={\frac {\partial A_{z}}}{\partial y}-{\partial A_{y}}}{\partial z}}}\ed}}}}}}}?$

$(\operatorname {curl} \mathbf {A} )_{y}$ $(\operatorname {curl} \mathbf {A} )_{y}$ $(\operatorname {curl} \mathbf {A} )_{y}$ ) y ${\$ ) $(\operatorname {curl} \mathbf {A} )_{z}$ ${y}$ 및 $(\operatorname {curl} \mathbf {A} )_{y}$ $(\operatorname {curl} \mathbf {A} )_{z}$ ( $(\operatorname {curl} \mathbf {A} )_{z}$ $(\operatorname {curl} \mathbf {A} )_{z}$ $(\operatorname {curl} \mathbf {A} )_{z}$ ) z ${\$ { $A}$ )_ ${z}$ 에 대한 식도 같은 방법으로 찾을 수 있다 $(\operatorname {curl} \mathbf {A} )_{z}$ .

원통 유도

${\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )\,d\phi \,dz-A_{\rho }(\rho )\rho \,d\phi \,dz+A_{\phi }(\phi +d\phi )\,d\rho \,dz-A_{\pi }\,d\rho \,dz+A_{z}(z+dz)\,d\rho \,(\rho +d\rho /2)\,d\phi -A_{z}(z)\,d\rho (\rho +d\rho /2)\,d\phi }{\rho \,d\phi \,d\rho \,dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}$

${\displaystyle{\begin{정렬}(\operatorname{컬}\mathbf{A})_{\rho}&, =\lim _{S^{\perp{\boldsymbol{\hat{\rho}}}}\to 0}일 경우{\frac{\int_{\partial S}\mathbf{A}\cdot d\mathbf{\ell}}{\iint_{S}dS}}\\&, =ᆶ(z)(\rho +d\rho)\,d\phi(}+A_ᆸ(\phi +d\phi)\,dz-A_ᆹ(\phi)\,dz{(\rho +d\rh.o)\,d\p안녕 \dz}\\&=-{\frac {\partial A_{\phi }}{\partial z}+{\partial z}{1}{\rho}}}}{\partial A_{z}}}{\partial \pi }}}}}}}}$

{\displaystyle{\begin{정렬}(\operatorname{컬}\mathbf{A})_{\phi}&, =\lim _{S^{\perp{\boldsymbol{\hat{\phi}}}}\to 0}일 경우{\frac{\int_{\partial S}\mathbf{A}\cdot d\mathbf{\ell}}{\iint_{S}dS}}\\&, =ᆴ(\rho)\,dz-A_ᆵ(\rho +d\rho)\,dz+A_ᆶ(z+dz)\,d\rho -A_ᆷ(z)\,d\rho}{\,dzd\rho}}\\&, =-{\frac{\partial A_{z}}{\parti\rho }}}{\frac {\partial A_{\rho }}}{\partial z}\end{arged}}}}

{\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\boldsymbol {\hat {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}

{\displaystyle{\begin{정렬}\operatorname{ 곱슬곱슬하게 하다.}, =(\operatorname{컬}\mathbf{A})_{\rho}{\hat{\boldsymbol{\rho}}}+(\operatorname{컬}\mathbf{A})_{\phi}{\hat{\boldsymbol{\phi}}}+(\operatorname{컬}\mathbf{A})_{z}{\hat{\boldsymbol{z}}}\\&, =\left({\frac{1}{\rho}}{\frac{\partial A_{z}}{\phi\partial}}-{A}및 \mathbf.{\frac{\partial A_{\phi }}{\partial z}\오른쪽){\hat {\boldsymbol {\rho}}+\좌({\frac {\partial A_{\rho}}}{\partial z}-{\frac {\partial A_{z}}{\partial \rho}}\우){\hat{\boldsymbol {\phi }}+{\frac {1}{\rho }}\frac {1}{\partial \rho }{\partial \rho }{\partial \pho }{\partial \phi }\rig){\hat {\\hatsymbol {z}\end{aigned}}

구면 유도

${\displaystyle{\begin{정렬}\operatorname{div}, =\lim _{V\to 0}{\frac{\iint_{\partial V}\mathbf{A}\cdot d\mathbf{S}}{\iiint_{V}dV}}\\&, =ᆶ(r+dr)(r+dr)\,d\theta \,(r+dr)\sin \theta \,d\phi -A_ᆷ(r)r\,d\theta \,r\sin \theta \,d\phi +A_ᆸ(+d\theta\theta)\sin(+d\theta\theta)r\,dr\,d\phi -A_{\theta}({A}및 \mathbf.\theta)\sin(\theta)r\,dr\,d\phi +A_ᆭ(\phi +d\phi)r\,dr\,d\theta -A_ᆮ(\phi)r\,dr\,d\theta}{dr\,r\,d\theta \,r\sin \theta \,d\phi}}\\&, ={\frac{1}{r^{2}}}{\frac{\partial(r^{2}A_{r})}{r\partial}}+{\frac{1}{r\sin \theta}}{\frac{\partial(A_{\theta}\sin \theta)}{\theta\partial}}+{\frac{1}{r\sin \theta}}{\frac{\partial A_{\phi}.}{\p아티알 \phi }}\end{aigned}}$

${\displaystyle{\begin{정렬}(\operatorname{컬}\mathbf{A})_{r}=\lim _{S^{\perp{\boldsymbol{\hat{r}}}}\to 0}일 경우{\frac{\int_{\partial S}\mathbf{A}\cdot d\mathbf{\ell}}{\iint_{S}dS}}&=ᆴ(\phi)r\,d\theta +A_ᆵ(+d\theta\theta)r\sin(+d\theta\theta)\,d\phi -A_ᆶ(\phi +d\phi)r\,d\theta -A_{\phi}(\thet.a)r\sin(\theta )\,d\phi }{r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}$

${\displaystyle{\begin{정렬}(\operatorname{컬}\mathbf{A})_{\theta}=\lim _{S^{\perp{\boldsymbol{\hat{\theta}}}}\to 0}일 경우{\frac{\int_{\partial S}\mathbf{A}\cdot d\mathbf{\ell}}{\iint_{S}dS}}&=ᆵ(r)r\sin\theta\,d\phi +A_ᆶ(\phi +d\phi)\,dr-A_ᆷ(r+dr)(r+dr)\sin\theta \,d\phi -A_ᆸ(\phi)\,dr}{dr\,r\sin cm이다.theta \d\phi }\&={\frac {1}{r\partial A_{r}}{{\frace \partial \partial \phi }}{\partial \partial }{1}{{{1}}}}{A_{\partial r\end}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}\partial r\partial r\frined}}}}$

${\displaystyle{\begin{정렬}(\operatorname{컬}\mathbf{A})_{\phi}=\lim _{S^{\perp{\boldsymbol{\hat{\phi}}}}\to 0}일 경우{\frac{\int_{\partial S}\mathbf{A}\cdot d\mathbf{\ell}}{\iint_{S}dS}}&=ᆵ(\theta)\,dr+A_ᆶ(r+dr)(r+dr)\,d\theta -A_ᆷ(+d\theta\theta)\,dr-A_ᆸ(r)r\,d\theta}{r\,dr\,d\theta}}\\&, =.{\frac{1}{{r}}{\frac {\partial (rA_{\theta }}}}{\partial r}-{\prac {1}{r}{\partial A_}{\partial \theta }}}}}}}}$

$\operatorname {curl} \mathbf {A} =(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \pi }}\오른쪽){\hat{\boldsymbol{r}}+{\frac {1}{1}}\좌({\frac {1}{\sin \sin \pinal A_{r}}}{\partial \phi }}{A_{\partial r\}}오른쪽){\hat{\boldsymbol{\thea}}+{\frac {1}{1}{r}\왼쪽({\frac {\partial (rA_{\teta }}}}{\partial r}{\partial A_{r}}{\partial \ta }}오른쪽){\hat {\\hatsymbol {\phi }}}$

단위 벡터 변환식

좌표 매개변수 u의 단위 벡터는 ${\boldsymbol {\vec {r}}}$ ${\boldsymbol {\hat {u}}}$ 의 작은 양의 변화가 위치 벡터 r → {\ $displaystyle$ {\ $boldsymbol {\vec{r}}$ ${\boldsymbol {\hat {u}}}$ ${\$ 방향으로 ${\boldsymbol {\hat {u}}}$ 변경되도록 ${\boldsymbol {\vec {r}}}$ 정의된다.

그러므로

{\displaysymbol {\\bech{r}}}\over \cHBU}={\s}\over \propersymbol{\hat{u}}}}}}}}}}

여기서 s는 호 길이 매개변수다.

체인 규칙에 따라 $v_{j}$ 좌표계 $u_{i}$ {\ $displaystyle u_{i}$ 및 $v_{j}$ j ${\$ 의 두 세트에 대해,

d{\boldsymbol {\vec {r}}}=\sum _{i}{\partial {\boldsymbol {\vec {r}}} \over \partial u_{i}}du_{i}=\sum _{i}{\partial {s} \over \partial u_{i}}{\boldsymbol {\hat {u_{i}}}}du_{i}=\sum _{j}{\partial {s} \over \partial v_{j}}{\boldsymbol {\hat {v_{j}}}}dv_{j}=\sum _{j}{\partial {s} \over \partial v_{j}}{\boldsymbol {\hat {v_{j}}}}\sum _{i}{{}{v_{j}} \over \cHB_{i}}=\sum _{i}\sum _{j}}{{j}}} \over \cHB_{v_{j}}}}{{v_{j}}}}} \over \cHatsymbol{{v_}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}{{{{{{{i}}}}}}}}}}}

$i^{th}$ i $i^{th}$ $i^{th}$ ${\$ 성분을 $i^{th}$ 분리한다. $i{\neq }k$ $i{\neq }k$ $i{\neq }k$ ${\displaystyle i{\neq }k$ 의 경우 $du_{k}=0$ $du_{k}=0$ = $du_{k}=0$ $du_{k}=0$ 을(를) 두십시오 $du_{k}=0$ $du_{i}$ 다음 d $du_{i}$ $du_{i}$ ${\$ 양쪽으로 나누어 다음을 $du_{i}$ 얻으십시오.

{\s}\over \symbol{{i}}{\hat {\hat {u_{i}}}}}=\sum _{j}}\over v_{j}{v_{j}}}}}\dismbol {v_{j}}}}}}}}}}

참고 항목

참조

^ Jump up to: ^a ^b ^c ^d ^e ^f ^g ^h Griffiths, David J. (2012). Introduction to Electrodynamics. Pearson. ISBN 978-0-321-85656-2.
^ Arfken, George; Weber, Hans; Harris, Frank (2012). Mathematical Methods for Physicists (Seventh ed.). Academic Press. p. 192. ISBN 9789381269558.
^ Weisstein, Eric W. "Convective Operator". Mathworld. Retrieved 23 March 2011.

외부 링크

이러한 연산자 중 일부를 원통형 좌표와 구형 좌표로 생성하기 위한 Maxima Computer Algebra 시스템 스크립트.

[griffiths-1] Jump up to: ^a ^b ^c ^d ^e ^f ^g ^h Griffiths, David J. (2012). Introduction to Electrodynamics. Pearson. ISBN 978-0-321-85656-2.

[2] Arfken, George; Weber, Hans; Harris, Frank (2012). Mathematical Methods for Physicists (Seventh ed.). Academic Press. p. 192. ISBN 9789381269558.

[Mathworld-3] Weisstein, Eric W. "Convective Operator". Mathworld. Retrieved 23 March 2011.

[1]

α

[2]

[3]

Search