넬더-메드법

Nelder-Mead 방법(활강 단순화 방법, 아메바 방법 또는 폴리토페 방법)은 다차원 공간에서 객관적 함수의 최소 또는 최대치를 찾기 위해 일반적으로 사용되는 숫자 방법이다.직접 검색 방식(함수비교 기준)으로 파생상품을 알 수 없는 비선형 최적화 문제에 적용하는 경우가 많다.그러나 넬더-미드 기법은 대체 방법으로 해결할 수 있는 문제에 대해 논역적 지점으로^[1] 수렴할 수 있는 경험적 접근법이다.^[2]

넬더-미드 기법은 1965년 존 넬더와 로저 미드가 써들리 외 방법의 개발로 제안하였다.^[3][4]

개요

방법은 심플렉스(simplex)의 개념을 사용하며, 이 개념은 n차원에서 n + 1 정점의 특수 폴리토프다.단순화의 예로는 선상의 선 세그먼트, 평면의 삼각형, 3차원 공간의 사면체 등이 있다.

이 방법은 객관적 기능이 완만하게 변화하고 단수일 때 n개의 변수에 대한 문제의 국소적 최적치에 가깝다.일반적인 구현은 기능을 최소화하고$,{\displaystyle }$ 우리는 - ${\displaystyle f}$( x${\displaystyle }$) {\$displaystyle f(\mathbf {x}$ ) ${\displaystyle -f(\$mathbf ${x}$ $)\}$을(를) 최소화하여$$ $f{\displaystyle }$( ${\displaystyle x\mathbf{}}$${\displaystyle }$) ${\$displaystyle -f {x}을$($으)를 최대화한다.

예를 들어 현수교 엔지니어는 각 스트럿, 케이블 및 교각의 두께를 선택해야 한다.이러한 요소들은 상호의존적이지만, 어떤 특정 요소 변경의 영향을 시각화하기는 쉽지 않다.그러한 복잡한 구조물의 시뮬레이션은 종종 실행하는데 극도로 계산적으로 비용이 많이 들고, 실행당 시간 이상이 소요될 수 있다.Nelder-Mead 방법은 원래 변종에서 나중에 설명한 축소 연산을 제외하고 반복당 2회 이하의 평가를 요구하는데, 이는 다른 직접 검색 최적화 방법에 비해 매력적이다.그러나 제안된 최적화에 대한 전체 반복 횟수는 많을 수 있다.

n 치수의 Nelder-Mead는 심플렉스(simplex)로 배열된 n + 1의 시험 지점 세트를 유지한다.그런 다음 새로운 시험 지점을 찾기 위해 각 시험 지점에서 측정한 목표 함수의 동작을 추론하고 오래된 시험 지점 중 하나를 새로운 시험 지점으로 교체하여 기법을 진행시킨다.가장 간단한 접근법은 최악의 점을 나머지 n개의 점의 중심을 통해 반사되는 점으로 대체하는 것이다.이 지점이 가장 좋은 현재 지점보다 좋다면 이 선을 따라 기하급수적으로 스트레칭을 해 볼 수 있을 것이다.반면에, 만약 이 새로운 지점이 이전 가치보다 훨씬 낫지 않다면, 우리는 계곡을 가로질러 가고 있기 때문에, 우리는 더 나은 지점으로 단순함을 축소한다."수리적 레시피"의 알고리즘에 대한 직관적인 설명:

내리막 심플렉스 방식은 이제 일련의 단계를 거치게 되는데, 대부분의 스텝은 기능이 가장 큰 심플렉스("최고점")의 점을 심플렉스 반대면을 통해 더 낮은 지점으로 이동하기만 하면 된다.이러한 단계를 반사라고 하며, 단순함의 부피를 보존하기 위해 구성된다(따라서 비생식성을 유지한다).그렇게 할 수 있을 때, 그 방법은 심플렉스를 한 방향으로 혹은 다른 방향으로 확장시켜 더 큰 단계를 밟는다.'밸리 바닥'에 이르면 그 방법은 가로 방향으로 저절로 수축되어 골짜기로 흘러내려 한다.심플렉스가 '바늘의 눈'을 통과하려 하는 상황이 발생하면 사방으로 수축해 가장 낮은(최상의) 지점을 중심으로 스스로 끌어당긴다.

현대적 최적화 방법과 달리, Nelder-Mead 휴리스틱스는 현대적 방법에 필요한 것보다 더 강한 조건을 만족시키지 않는 한, 논스테이션 포인트로 수렴할 수 있다.^[1]넬더-미드 휴리스틱스에 대한 현대의 개선은 1979년부터 알려져 있다.^[2]

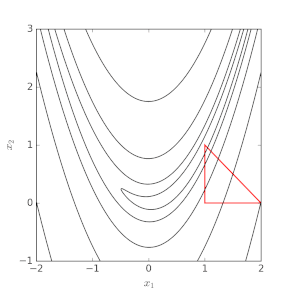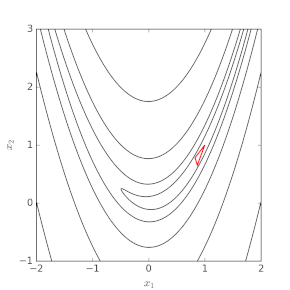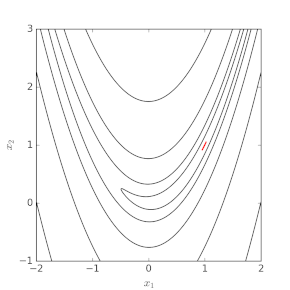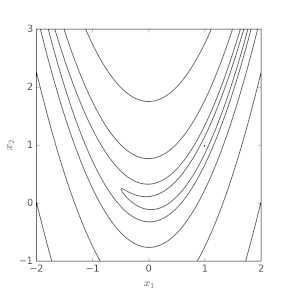
해결되는 문제의 실제 성격에 따라 많은 변형이 존재한다.일반적인 변종은 구배 방향(가장 가파른 하강)을 대략적으로 따르는 일정한 크기의 소형 심플렉스(simplex)를 사용한다.표고 지도에서 작은 삼각형이 계곡에서 로컬 하단으로 넘어가는 모습을 시각화하십시오.이 방법은 융통성 있는 다면체법으로도 알려져 있다.그러나 이것은 별로 흥미가 없는 분야에서는 작고 불필요한 단계를 만들기 때문에 이 글에서 기술된 방법에 대해 저조한 성과를 보이는 경향이 있다.

NM 알고리즘의 가능한 한 가지 변화

(이것은 원본 Nelder-Mead 기사의 절차에 가깝다.)

We are trying to minimize the function ${\displaystyle f(\mathbf {x} )}$, where ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$. Our current test points are ${\displaystyle \mathbf {x} _{1},\ldots ,\mathbf {x} _{n+1}}$.

1. 정점의 값에 따라 정렬한다.

${\displaystyle f(\mathbf {x} _{1})\leq f(\mathbf {x} _{2}\leq \cdots \leq f(\mathbf {x} _{n+1})).}$

메서드가 중지되어야 하는지 여부를 확인하십시오.아래 종료를 참조하십시오.때때로 부적절하게 "융합"이라고 불린다.

2. $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\${${\displaystyle {\mathrm{x}}_{}}$$} _{o},$ x ${\displaystyle {}_{}}$+ 1 ${\$를 제외한 모든 점의 중심인$$x o를 계산한다$.$

3. 반사

보다 보다 작은${\displaystyle {}_{}}$ = x o +${\displaystyle {}_{}{\mathrm{\alpha }}_{}}$( x${\displaystyle {\mathbf{}}_{}}$ - x n${\displaystyle {}_{}}$+ 1${\displaystyle {}_{}}$)${\displaystyle {}_{}}${\$displaystyle \mathbf {x} _{r}=\mathbf {x} _{o}-\mathbf${$x$$}$$_{n+1$}을$($으)로 $계산하십시오.$

반사된 지점이 두 번째 최악의 지점보다 낫지만 좋은 지점보다 낫지 않은 경우, 즉 ( ) ( r)< f( ) ${\displaystyle f(\mathbf {x} _{1})\leq f(\mathbf {r} _{r})(\mathbf$ {x}$_{n$}, $_{$n}}}, $,,$)

그런 다음 최악의 점 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$+ 1 ${\$을(를) 반사된 $점{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$$_{r}$로 교체하여 새 심플렉스를 구하고 1단계로 이동하십시오.

4. 확장

지금까지 반사된 점이 가장 좋은 점이라면 (x )<( )${\displaystyle f(\mathbf {x} _{r})<f(\mathbf$ {x$} _{1$}),

다음 확장된 점 x ${\displaystyle {}_{}}$= ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle \gamma }$(${\displaystyle {}_{}}$ r -${\displaystyle {}_{}{\mathbf{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle \mathbf {x} _{e}=\mathbf {x} _{o}+\mathbf {x}(\mathbf {x})$를 ${\displaystyty \1$로 계산한다.

확장 지점이 반사 지점보다 나은 경우, ( )< f( ){\$displaystyle f(\mathbf {x} _{e})<f(\mathbf {x} _{r})$,

그런 다음 최악의 지점 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$+ ${\displaystyle {}_{}}$ ${\$ $\$$mathbf {x} _{n+1}$을(를) $확장{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$x e {\$displaystyle$ \$mathbf {x}$ _{$e}$로 교체하여 새 심플렉스를 구하고$$ 1단계로 이동하십시오.

그렇지 않으면 최악의 점 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$+ 1 ${\$을(를) 반사된 ${\displaystyle {}_{}}$ $x{\displaystyle {\mathbf{}}_{}}$ ${\$로 교체하여$$ 새 심플렉스를 구하고 1단계로 이동하십시오.

5. 수축

${\displaystyle \mathrm{여기}}$서 $f{\displaystyle }$( x ${\displaystyle {}_{}}$) ${\displaystyle \ge }$ f${\displaystyle }$( ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle$ f$(\mathbf {x} _{r})\geq f(\mathbf {x} _{n})$. ($참고{\displaystyle {\mathbf{}}_{}}$: ${\displaystyle {}_{}}$ n ${\$ {$x} _{n$} _{n$})$가 두 번째 또는 "가장 높은 값보다 "다음"인$$ 것이 확실하다.)

( )< f( + ) ${\displaystyle$ f$(\mathbf {x} _{r})<f(\mathbf {x} _{n+1})$인 경우

then compute the contracted point on the outside ${\displaystyle \mathbf {x} _{c}=\mathbf {x} _{o}+\rho (\mathbf {x} _{r}-\mathbf {x} _{o})}$ with ${\displaystyle 0<\rho \leq 0.5}$.

수축된 점이 반사된 점보다 나은 경우 즉 ( c)< f( )${\displaystyle f(\mathbf {x} _{c})<f(\mathbf {x} _{r})},$

그런 다음 최악의 점 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$+ 1 ${\$을(를) $수축$된 점 ${\displaystyle {}_{}}$ ${\$로 교체하여 새 심플렉스를 구하고$$ 1단계로 이동하십시오.

그렇지 않으면 6단계에 도달한다.

$f{\displaystyle }$( ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle \ge }$ ${\displaystyle f}$( ${\displaystyle {\mathrm{x}}_{}}$ n${\displaystyle {}_{}}$+ 1${\displaystyle {}_{}}$) ${\displaystyle f(\mathbf {x} _{r})\geq f(\mathbf {x} _{n+1})$인 경우$,$

then compute the contracted point on the inside ${\displaystyle \mathbf {x} _{c}=\mathbf {x} _{o}+\rho (\mathbf {x} _{n+1}-\mathbf {x} _{o})}$ with ${\displaystyle 0<\rho \leq 0.5}$.

만약 그가 수축된 점이 최악의 지점보다 낫다면, 즉, ( )< ( + 1){\$displaystyle$ f$(\mathbf {x} _{c})<f(\mathbf {x} _{n+1$

그런 다음 최악의 점 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {\mathrm{n}}_{}}$+ 1 ${\$을(를) $수축$된 점 ${\displaystyle {}_{}}$ ${\$로 교체하여 새 심플렉스를 구하고$$ 1단계로 이동하십시오.

그렇지 않으면 6단계에 도달한다.

6. 수축

최량(x ${\displaystyle {\mathrm{}}_{}}$ ${\$을 제외한 모든 점을 다음으로 교체하십시오.

${\displaystyle {\mathbf{x}}_{}}$ ${\displaystyle {}_{}}$= x ${\displaystyle {}_{}}$+ ${\displaystyle \sigma }$( ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$- ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle \mathbf {x} _{i}=\mathbf {x} _{1}+\mathbf$ {$x}(\mathbf {x}-\mathbf {$x}) _{1} 단계로 $이동하십시오.$

참고: $\alpha {\displaystyle }$ ${\displaystyle \alpha$ $\},$ $\gamma {\displaystyle }$ ${\displaystyle \gamma },$$\rho {\displaystyle }$ ${\displaystyle \rho },$ $\sigma {\displaystyle }$ ${\displaystyle \sigma }$은 각각 반사, 팽창, 수축 계수, 수축 계수다$$.표준 값은 $\alpha {\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \알파 =1},$$\gamma {\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle \gamma =2},$${\displaystyle \rho \mathrm{}}$ =${\displaystyle }$1${\displaystyle }$/ 2 ${\displaystyle \rho$ =$1/2},$$$$\sigma$ =${\displaystyle }$1 /${\displaystyle 2\mathrm{}}$ ${\displaystystyle$\sigma $=1/$2}이다.

반사의 경우, ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$ ${\$${$$n+1}$는 정점들 사이에서 연관 값이 더 높은 정점이기 때문에, 모든 정점 ${\displaystyle {}_{}}$ i ${\$$${$x}$$$$_{n+1}$의 반사에서 더 낮은 값을 찾을 수 있을 것으로 예상할 수 있다.$_{$${\displaystyle {}_{}}$$}}$을(를) 제외하고$$ ${\displaystyle {\mathrm{x}}_{}}$ n${\displaystyle {}_{}}$+ 1 ${\$

확장의 경우, 반사점 $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$이 정점을 따라 새로운 최소값이라면$$ $x{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$에서 $x$ ${\displaystyle {}_{}}$ ${\$까지의 방향을 따라 흥미로운 값을 찾을 수 있을 것으로 기대할 수 있다.

수축과 관련하여 ( )> ( x ) ${\displaystyle f(\mathbf {x} _{r})>f(\mathbf {x} _{n$})>>f(\mathbf {n$}$ $_{n$가 되면 모든 $꼭지점{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ i ${\$에 의해 형성된 심플렉스 안에 더 나은 값이 있을 것으로 기대할 수 있다$.$

마지막으로, 수축은 가장 큰 지점에서 멀리 떨어져 수축하는 희귀한 사례를 다루며$,$ 비음향적 최소치에 충분히 근접할 수 없는 어떤 $것$을 f${\displaystyle f}$를 증가시킨다.그 경우 우리는 더 단순한 경관을 찾으려는 기대에서 최저점을 향해 수축한다.그러나 내시는 유한정밀 산술은 때때로 실제로 심플렉스를 축소하지 못할 수 있다는 점에 주목하고, 실제로 크기가 축소되는 체크도 실행했다.^[6]

초기 심플렉스

초기 심플렉스는 중요하다.실제로 너무 작은 초기 단순화는 로컬 검색으로 이어질 수 있으며, 결과적으로 NM이 더 쉽게 고착될 수 있다.그래서 이 심플렉스는 문제의 본질에 의존해야 한다.그러나 원문에서는 각 차원을 차례로 따라 고정된 스텝으로 생성된 다른 점들과 함께 초기 $포인트$가 x ${\displaystyle {\mathrm{}}_{}}${\$displaystyle \mathbf{x$ $_{1$}로 주어지는 심플렉스(simplex)를 제안했다.따라서 이 방법은 $x{\displaystyle \mathbf{}}$ ${\$를) 구성하는 변수의 스케일링에 민감하다$.$

종료

반복 주기를 깨기 위해서는 기준이 필요하다.Nelder와 Mead는 현재 심플렉스 함수 값의 표본 표준 편차를 사용했다.이러한 점이 어느 정도 허용오차 이하로 떨어지면 주기가 정지되고 제안된 최적점으로서 심플렉스 내 최저점이 반환된다.매우 "평평한" 함수는 큰 도메인에 걸쳐 거의 동일한 함수 값을 가질 수 있으므로 솔루션이 허용오차에 민감하게 반응한다는 점에 유의하십시오.내시는 수축에 대한 시험을 또 다른 종료 기준으로 추가한다.^[6]반복이 수렴되는 동안 프로그램이 종료된다는 점에 유의하십시오.

참고 항목

참조

추가 읽기

• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 978-0-486-43227-4.
• Coope, I. D.; Price, C. J. (2002). "Positive Bases in Numerical Optimization". Computational Optimization & Applications. 21 (2): 169–176. doi:10.1023/A:1013760716801. S2CID 15947440.
• Gill, Philip E.; Murray, Walter; Wright, Margaret H. (1981). "Methods for Multivariate Non-Smooth Functions". Practical Optimization. New York: Academic Press. pp. 93–96. ISBN 978-0-12-283950-4.
• Kowalik, J.; Osborne, M. R. (1968). Methods for Unconstrained Optimization Problems. New York: Elsevier. pp. 24–27. ISBN 0-444-00041-0.
• Swann, W. H. (1972). "Direct Search Methods". In Murray, W. (ed.). Numerical Methods for Unconstrained Optimization. New York: Academic Press. pp. 13–28. ISBN 978-0-12-512250-4.

외부 링크

• Rosenbrok 바나나 기능으로 Nelder-Mead (Downhill Simplex) 설명 및 시각화
• John Burkardt: Matlab의 Nelder-Mead 코드 - Nelder-Mead 방법의 변화는 Matlab 함수 fminsearch에 의해서도 구현된다는 점에 주목한다.
• SciPy 라이브러리의 Python에서 Nelder-Mead 최적화.
• Nelder-mead - Nelder-Mead 방법의 Python 구현
• SOVA 1.0(프리웨어) - 다양한 애플리케이션을 위한 Simplex 최적화
• [1] - HillStormer, Nelder Mead에 의한 비선형, 다변량 및 선형 제약 Simplex Optimization을 위한 실용적인 도구.