그룹 테스트

통계학이나 결합수학에서 집단검사는 특정 대상을 개별 검정이 아닌 항목군에서 검정으로 식별하는 작업을 세분화하는 어떤 절차다.1943년 로버트 도프먼에 의해 처음 연구된 집단시험은 광범위한 실용적 응용에 적용할 수 있는 비교적 새로운 응용 수학 분야로 오늘날에도 활발한 연구 영역이다.

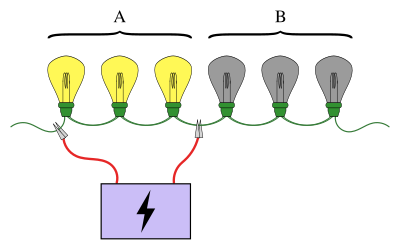
그룹 테스트의 익숙한 예로는 일련의 전구가 직렬로 연결되어 있는데, 전구 중 정확히 하나가 고장 난 것으로 알려져 있다.목표는 최소한의 테스트 횟수를 사용하여 고장 난 전구를 찾는 것이다(테스트의 경우 전구 일부가 전원 공급 장치에 연결되어 있을 때).간단한 접근법은 각 전구를 개별적으로 시험하는 것이다.그러나, 많은 수의 전구가 있을 때 전구를 그룹으로 묶는 것이 훨씬 더 효율적일 것이다.예를 들어, 전구의 전반부를 한 번에 연결함으로써, 한 번의 시험으로 전구의 반을 배제하면서, 어느 반의 전구가 고장 난 전구가 들어 있는지 판단할 수 있다.

그룹 시험을 수행하기 위한 계획은 간단하거나 복잡할 수 있으며 각 단계에서 관련된 시험은 다를 수 있다.다음 단계의 시험이 이전 단계의 결과에 의존하는 계획을 적응 절차라고 하는 반면, 모든 시험이 사전에 알려지도록 설계된 체계를 비적응 절차라고 한다.비적응적 절차에 관련된 시험의 체계 구조를 풀링 설계라고 한다.

집단 테스트는 통계, 생물학, 컴퓨터 과학, 의학, 공학, 사이버 보안을 포함한 많은 응용 프로그램을 가지고 있다.인간 게놈 프로젝트에 의해 이러한 시험 계획에 대한 현대의 관심이 다시 불붙었다.^[1]

기본 설명 및 용어

수학의 많은 영역과 달리 집단 테스트의 기원은 한 사람이 쓴 보고서인^[2] 로버트 도프만으로 거슬러 올라갈 수 있다.^[3]그 동기는 2차 세계 대전 동안 미국 공중 보건국과 선택적 서비스 기관이 유도를 위해 소집된 모든 매독 남성들을 제거하기 위한 대규모 프로젝트에 착수했을 때 일어났다.매독을 검사하는 것은 그들로부터 혈액 샘플을 채취한 다음 그 샘플을 분석하여 매독의 유무를 결정하는 것이다.그 당시 이 시험을 수행하는 것은 비용이 많이 들었고, 모든 군인들을 개별적으로 테스트하는 것은 매우 비싸고 비효율적이었을 것이다.^[3]

병사가$$ $n명$이라고 가정할 경우, 이 $테스트{\displaystyle }$ 방법은 n명 ${\displaystyn}$개의$$ 테스트로 이어진다.만약 많은 사람들이 감염되었다면, 이 방법은 합리적일 것이다.그러나, 남성들 중 극히 일부만이 감염되었을 가능성이 더 높은 경우, 훨씬 더 효율적인 검사 계획을 달성할 수 있다.보다 효과적인 검사 계획의 실현 가능성은 다음과 같은 특성에 달려 있다: 군인들은 그룹으로 묶을 수 있고, 각 그룹에서 혈액 샘플을 함께 결합할 수 있다.그런 다음, 조합된 샘플은 그룹에서 적어도 한 명의 군인이 매독에 걸렸는지 확인하기 위해 테스트될 수 있다.이것이 그룹 테스트의 핵심 아이디어다.이 그룹에 속한 병사 중 한 명 이상이 매독에 걸리면 검사가 낭비된다(어느 병사를 찾으려면 더 많은 검사를 수행해야 한다).반면에, 만약 수영장에 있는 어느 누구도 매독에 걸리지 않는다면, 그 그룹의 모든 군인들은 단 한 번의 시험으로 제거될 수 있기 때문에, 많은 시험들이 저장된다.^[3]

집단이 양성반응을 일으키게 하는 품목을 일반적으로 불량품(이것들은 부서진 전구, 매독남 등)이라고 부른다.$흔히{\displaystyle }$ 총 항목 수는 n ${\displaystyle n}$으로 표시되고$$ $d{\displaystyle }$ ${\displaystyle d}$은(는) 알려진 것으로 가정할 경우 불량품의 수를 나타낸다$$.^[3]

그룹 테스트 문제 분류

그룹 시험 문제에 대해서는 두 가지 독립적인 분류가 있다. 모든 그룹 시험 문제는 적응형 또는 비적응형이며 확률형 또는 결합형이다.^[3]

확률론적 모형에서 불량품목은 일부 확률 분포를 따르는 것으로 가정하며, 목적은 모든 품목의 불량성을 식별하는 데 필요한 시험의 예상 횟수를 최소화하는 것이다.한편, 조합군 시험을 통해, 목표는 '최악의 경우 시나리오', 즉 미니맥스 알고리즘을 만드는 데 필요한 시험 횟수를 최소화하는 것이며 불량품 분포에 대한 지식은 가정하지 않는다.^[3]

다른 분류인 적응성은 어떤 항목을 시험으로 그룹화할지 선택할 때 어떤 정보를 사용할 수 있는지에 관한 것이다.일반적으로, 위의 전구 문제에서와 같이 어떤 항목을 테스트할 것인가는 이전 시험의 결과에 따라 달라질 수 있다.테스트를 수행한 다음 결과(및 모든 과거 결과)를 사용하여 수행할 다음 테스트를 결정하는 알고리즘을 적응형이라고 한다.반대로 비적응 알고리즘에서는 모든 시험이 사전에 결정된다.이 아이디어는 시험이 단계별로 구분되는 다단계 알고리즘으로 일반화할 수 있으며, 다음 단계의 모든 시험은 이전 단계의 시험 결과에 대한 지식만으로 사전에 결정해야 한다.적응형 알고리즘은 설계에 있어 훨씬 더 많은 자유를 제공하지만, 적응형 그룹 시험 알고리즘은 비적응형 알고리즘에 대해 불량품 집합을 식별하는 데 필요한 시험 횟수에 일정 요인 이상 개선되지 않는 것으로 알려져 있다.^[4][3]이와 더불어 비적응적 방법은 모든 이전 시험의 결과를 먼저 분석하지 않고 연속적인 시험을 진행할 수 있기 때문에 종종 실무에서 유용하며, 시험 프로세스의 효과적인 분포를 가능하게 한다.

변형 및 확장

그룹 테스트 문제를 확대하는 방법은 여러 가지가 있다.가장 중요한 것 중 하나는 시끄러운 집단 검사라고 불리며, 원래 문제에 대한 큰 가정을 다룬다: 시험은 오류가 없다는 것이다.그룹 테스트 문제는 그룹 테스트 결과가 잘못될 가능성이 있을 때(예: 테스트에 결함이 없을 때 양성으로 나오는 경우) 시끄러움이라고 한다.베르누이 소음 모델은 이 확률을 일정하게 $q{\displaystyle }$ ${\displaystyle q$이라고 가정하지만, 일반적으로 시험의 실제 불량품 수와 시험 품목 수에 따라 달라질 수 있다.^[5]예를 들어, 희석 효과는 시험에 더 많은 불량품(또는 시험된 숫자의 일부로 더 많은 불량품)이 있을 때 양성 결과가 더 가능성이 높다고 말해 모델링할 수 있다.^[6]소음이 많은 알고리즘은 항상 오류를 범할 확률이 0이 아닐 것이다(즉, 항목 레이블을 잘못 표시).

그룹 시험은 시험 결과가 세 개 이상 가능한 시나리오를 고려하여 확장할 수 있다.예를 들어, ${\displaystyle \mathrm{검정}}$ 결과 $0{\displaystyle \mathrm{},}$ 1 ${\displaystyle 0.1$} $및$ 2 +$${\$displaystyle 2^{+},$ 불량품 수가 1보다 크거나 알 수 없는 수의 불량품이 있을 수 있다$.$보다 일반적으로 일부 ${\displaystyle k\mathbb{}}$ ${\displaystyle \in }$ N ${\$ {$N}$에 대해 테스트$$ 결과 집합을 $0{\displaystyle \mathrm{},}$ ${\displaystyle 1}$,${\displaystyle {}^{}}$+ ${\$ k$^{+}}}}$로 간주할 수 있다$.$^[3]

또 다른 확장자는 시험할 수 있는 세트의 기하학적 제한을 고려하는 것이다.위의 전구 문제는 이러한 종류의 제한의 예로서 연속적으로 나타나는 전구만 시험할 수 있다.마찬가지로, 항목들은 원 또는 일반적으로 그물로 배열될 수 있으며, 여기서 시험은 그래프에서 사용 가능한 경로일 수 있다.또 다른 종류의 기하학적 제한은 그룹에서 시험할 수 있는 최대 항목 수에 관한 것일 수도 있고,^[a] 또는 그룹 크기가 균등해야 할 수도 있다.유사한 방법으로, 주어진 항목이 특정 수의 시험에만 나타날 수 있다는 제한을 고려하는 것이 유용할 수 있다.^[3]

그룹 테스트의 기본 공식을 리믹스하는 것을 계속하는 방법은 무궁무진하다.다음의 자세한 설명은 좀 더 이국적인 변종들에 대한 아이디어를 줄 것이다.'좋은-중간-나쁜' 모델에서 각 항목은 '좋은', '중간' 또는 '나쁜' 항목 중 하나이며, 시험 결과는 그룹 내 '최악' 항목의 유형이다.분계점군 시험에서 그룹의 불량품 수가 일부 분계점수 또는 비율보다 크면 시험 결과는 양수다.^[7]억제제를 사용한 집단 테스트는 분자 생물학에서 응용이 가능한 변형이다.여기서 억제제라고 하는 제3종류가 있는데, 적어도 하나의 결함이 있고 억제제가 없으면 시험 결과는 양성이 된다.^[8]

역사와 발전

발명 및 초기진행

집단 실험의 개념은 1943년 로버트 도프만이 수학통계연보(Notes of^[2] Mathematical Statistics)^[3][b]에 발표한 짧은 보고서에서 처음 도입했다.그룹 테스트에 관한 모든 초기 연구와 마찬가지로 도프만의 보고서는 확률론적 문제에 초점을 맞췄으며, 집단 테스트라는 새로운 아이디어를 사용하여 주어진 군인들의 풀에서 모든 매독 남성들을 걸러내는 데 필요한 테스트의 예상 횟수를 줄이는 것을 목표로 삼았다.그 방법은 간단했다: 병사들을 일정한 크기의 그룹으로 묶고, 양성 그룹에 대한 개별 검사(1개 크기의 그룹으로 된 테스트 항목)를 사용하여 어떤 것이 감염되었는지 알아내는 것이었다.Dorfman은 이 전략의 최적 그룹 크기를 모집단의 결함 유병률에 대해 표로 표시했다.^[2]

1943년 이후, 집단 실험은 몇 년 동안 거의 손대지 않고 있었다.그 후 1957년에 스털렛은 도프만의 시술법을 개선했다.^[10]이 새로운 과정은 양성 그룹에 대해 개별 테스트를 다시 수행하는 것으로 시작되지만 결함이 확인되는 즉시 중단된다.그리고 나서, 그룹 내의 나머지 항목들은 모두 불량일 가능성이 매우 높기 때문에 함께 시험한다.

그룹 테스트의 첫 번째 철저한 치료는 소벨과 그롤이 이 주제에 대한 1959년 공식 논문에서 제공했다.^[11]그들은 유병률을 알 수 없는 경우에 대한 일반적인 설명과 더불어 다섯 가지 새로운 절차를 설명했으며, 최적의 절차에 대해서는 사용할 예상 시험 횟수에 대한 명시적인 공식을 제공했다.또한 이 논문은 집단 테스트와 정보 이론의 연결을 최초로 만들었으며, 집단 테스트 문제의 몇 가지 일반화를 논하고 이론의 몇 가지 새로운 응용을 제공하였다.

조합군 테스트

그룹 테스트는 $Li$의 ${\displaystyle s}$ - stage$$ 알고리즘의 도입으로 1962년 Li에 의해 조합 문맥에서 처음 연구되었다.^[12][3]Li proposed an extension of Dorfman's '2-stage algorithm' to an arbitrary number of stages that required no more than ${\displaystyle t={\frac {e}{\log _{2}(e)}}d\log _{2}(n)}$ tests to be guaranteed to find ${\displaystyle d}$ or fewer defectives among ${\displaystyle n}$ ite음극 테스트의 모든 항목을 제거하고 초기 풀에서처럼 나머지 항목을 그룹으로 나누는 것이 아이디어였다.이 작업은 개별 테스트를 수행하기 $전$에${\displaystyle }$s - ${\displaystyle 1}$ ${\displaystyle s-1}$번$$ 수행되어야 한다.

일반적으로 결합 집단 실험은 1973년에 카토나에 의해 더 완전하게 연구되었다.^[13]카토나는 비적응적 집단검사의 행렬표현을 도입하고, 비적응적 1-결함 사례에서 $t{\displaystyle }$= ${\displaystyle \lceil }$ ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle }$ (${\displaystyle n}$ )${\displaystyle \{}$ ${\displaystyle$ t$=\lceil \log_{2}(n)\rceil }$ 검사에서$$ 결함을 찾아내는 절차를 만들었는데, 이 또한 그가 최적임을 입증했다.

일반적으로 적응형 조합군 시험을 위한 최적의 알고리즘을 찾는 것은 어렵고, 집단 시험의 계산 복잡성은 파악되지 않았지만, 일부 복잡성 등급에서는 어려운 것으로 의심된다.^[3]그러나, 1972년에 일반화된 이항 분할 알고리즘의 도입으로 중요한 돌파구가 생겼다.^[14]일반화된 이진 분할 알고리즘은 양수를 테스트하는 그룹에 대해 이진 검색을 수행함으로써 작동하며, 정보 하한 검사 횟수 이하에서 단일 결함을 찾아내는 단순한 알고리즘이다.

두 개 이상의 불량품이 있는 시나리오에서 일반화된 이항 분할 알고리즘은 여전히 거의 최적인 ${\displaystyle \mathrm{결과}}$를 산출하며, $d{\displaystyle }$ ${\$$displaystyle d-1}$ $시험$의 경우, d {\$displaystyle d}$이(가$$) 불량품의 수입니다${\displaystyle .}$^[14]이에 대한 상당한 개선은 ${\displaystyle \mathrm{알레만}}$에 의해 2013년에 이루어졌으며, $필요$한 시험 횟수가 0.187d${\displaystyle }$+ 0.${\displaystyle 5}$ ${\displaystyle {\log }_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {}_{}}$(${\displaystyle d}$ ${\displaystyle )}$+${\displaystyle 5}$.5 ${\displaystyle 0.187d+0$ 미만이었다$.$$5$${\displaystyle \backslash log}$ $_{2}(d)+5.5}$은(는) n / d ${\displaystyle \ge }$ 38 ${\d/$ $및{\displaystyle }$ d$$ ${\displaystyle \ge }$ ${\displaystyle 10}$ ${\displaystyle d\geq 10}$일 때 정보 하한보다 높다$$$.$^[15]이는 바이너리 분할 알고리즘의 바이너리 검색을 테스트 그룹이 중복되는 복잡한 하위 알고리즘 집합으로 변경함으로써 달성되었다.이와 같이 불량품 수에 대해 알려진 수치 또는 상한을 갖는 적응성 결합군 시험 문제는 본질적으로 해결되었으며, 추가 개선의 여지가 거의 없다.

개인 시험이 언제 최소값인지에 대한 공개적인 질문이 있다.만일 n≤ 3후, 황과 왕 1981년에서 n≤ ⌊(5d+1)/2⌋{\displaystylen\leq \lfloor(5d+1)/2\rfloor}이 개별 시험 때 n을이minmax지 않다 minmax 3d{\displaystyle n>, D}.[16]현재 이 묶인:저것은 예민하다고 했던 것으로 추측, 개별 시험minmax 것으로 나타났다.d{\di$splaystyle n\leq 3d$^[17][c] 큰 n ${\displaystyle$ n}에$$대해 d ${\displaystyle {who\mathrm{}}_{}}$ n${\displaystyle }$/ ${\displaystyle 2_{}}$ ${\displaystyle {}_{}}$(${\displaystyle 3}$)${\displaystyle \mathrm{}\approx }$ 0${\displaystyle .369}$n${\displaystyle {}_{}}${\$displaysty d\geq$ $/\log$ _${3/2}($)\{3/2}($3)가$약 0.$369일$ 때 개별 테스트가 Minmax$.$^[18]

비적응성 및 확률론적 시험

비적응적 집단 시험의 주요 통찰력 중 하나는 집단 시험 절차가 반드시 성공해야 한다는 요구사항("결합" 문제)을 제거함으로써 상당한 이득을 얻을 수 있지만 오히려 각 항목에 잘못 라벨을 붙일 가능성은 낮지만 0이 아닌 확률("확률적" 문제)을 가질 수 있다는 것이다.불량품 수가 총 품목 수에 근접함에 따라 정확한 조합 솔루션은 확률론적 해결책보다 훨씬 더 많은 테스트를 필요로 하며 확률론적 해결책도 무증상적으로 작은 오류 확률만 허용한다고 알려져 있다.^[4][d]

In this vein, Chan et al. (2011) introduced COMP, a probabilistic algorithm that requires no more than ${\displaystyle t=ed(1+\delta )\ln(n)}$ tests to find up to ${\displaystyle d}$ defectives in ${\displaystyle n}$ items with a probability of error no more than ${\displaystyle n^{-$$\delta$ $\}\}\}.$^[5] $이것$은 t${\displaystyle }$=${\displaystyle O}$(d ${\displaystyle {\log }_{}}$ ${\displaystyle {2\mathrm{}}_{}}$⁡${\displaystyle n}$){\$displaystyle t=O(d\log _{2}n)}$ 하한에$$ 있는 상수 요인 안에 있다$.$^[4]

Chan 외 연구진(2011)은 또한 단순 소음 모델에 COMP의 일반화를 제공했으며, 이와 유사하게 명시적인 성능 한계를 생성했는데, 이는 다시 해당 하한보다 상수(시험 실패 가능성에 따라 달라짐)^[4][5]에 불과했다.일반적으로 베르누이 소음 사례에서 요구되는 시험 횟수는 소음 없는 경우보다 큰 일정한 요인이다.^[5]

앨드리지, 발다시니, 존슨(2014년)은 후처리 단계를 추가하는 COMP 알고리즘의 확장을 생산했다.^[19]그들은 DD라고 불리는 이 새로운 알고리즘의 성능이 COMP의 성능을 엄격히 능가한다는 것을 보여주었고, 이를 합리적인 최적치를 정의하는 가상 알고리즘과 비교함으로써 d ${\displaystyle {2\mathrm{}}^{}\mathrm{2n}}$ ${\displaystyle d^{2}\geqn$이 있는 시나리오에서 DD가 '본질적으로 최적'이라는 것을 보여주었다. 가상 알고리즘의 성능은 d < ${\displaystyle d^{2}<n$이 개선될 여지가 있음을 시사하는 동시에 이것이 얼마나 개선될 수 있는지를 시사한다.^[19]

조합군 시험 공식화

이 절에서는 집단 시험과 관련된 개념과 용어를 공식적으로 정의한다.

• The input vector, ${\displaystyle \mathbf {x} =(x_{1},x_{2},\dots ,x_{n})}$, is defined to be a binary vector of length ${\displaystyle n}$ (that is, ${\displaystyle \mathbf {x} \in \{0,1\}^{n}}$), with the j-th item being called defective if and only if ${\displaystyle x_j}$${\displaystyle =}$ ${\displaystyle 1}$ $[\displaystyle x_{j}=1$ 게다가 어떤 불량품이라도 '착한' 항목이라고 한다.

${\displaystyle \mathbf{x}}$ ${\$은(는) 불량품 집합을 설명하기 위한 것이다$$.x ${\$의 주요$$속성은 암시적 입력이라는 것이다$$.즉, $x{\displaystyle \mathbf{}}$ ${\$의 항목이 무엇인지에$$ 대한 직접적인 지식은 없으며, 이 항목은 일부 '시험'을 통해 추론할 수 있다.이것은 다음 정의로 이어진다.

• $x{\displaystyle \mathbf{}}$ ${\$를) 입력 벡터가 되도록$$ 한다.$세트$인 S ${\displaystyle \subseteq \{}$ ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle }$…,${\displaystyle n}$ ${\displaystyle \}}$ ${\displaystyle$S\$subseteq \{1,2,\dots,n\}}$을(를) 시험이라고 한다$$.테스트가 소음이 없는 경우, ${\displaystyle {테스트}_{}}$ 결과는 x $j{\displaystyle {}_{}}$= ${\displaystyle 1}$ ${\displaystyle x_{j}=1$}과$$ 같은 $j{\displaystyle }$ ${\displaystyle \in }$ S ${\displaystyle j\in S}$이$($가$)$ 있을 때 양성이며, 그렇지 않으면 음성이 된다.

따라서 그룹 테스트의 목표는 $x{\displaystyle \mathbf{}}$ ${\$을(를) 정확하게 또는 높은 수준의 확실성으로 결정할$$ 수 있는 '짧은' 일련의 테스트를 선택하는 방법을 마련하는 것이다.

• 그룹 테스트 알고리즘은 어떤 항목에 잘못 라벨을 붙이면 오류를 범한다고 한다(즉, 결함이 있는 품목은 불결함으로 표시하거나 그 반대로 표시).이것은 집단 테스트의 결과가 부정확한 것과 같은 것이 아니다.알고리즘이 오류를 범할 확률이 0이면 제로 오류라고 한다.^[e]
• ${\displaystyle t}$( ${\displaystyle d}$, ${\displaystyle n}$) ${\displaystyle t(d,n)}$은(는) 그룹화 알고리즘에 의해 오류 확률이 0인 $n{\displaystyle }$ ${\displaystyle n}$ 항목$$ 중 $d{\displaystyle }$ ${\displaystyle d}$ 불량품을$$ 항상 찾는 데 필요한 최소 테스트 수를 의미한다$$.동일한 양이지만 알고리즘이 비적응적이라는 제한과 함께 $t{\displaystyle \stackrel{}{}\text{'}(d}$, ${\displaystyle n}$) ${\displaystyle {\bar{t}(d,n)}$라는 표기법이 사용된다$$.

일반 경계

Since it is always possible to resort to individual testing by setting ${\displaystyle S_{j}=\{j\}}$ for each ${\displaystyle 1\leq j\leq n}$, it must be that that ${\displaystyle {\bar {t}}(d,n)\leq n}$. Also, since any non-adaptive testing procedure can be written as an adaptivealgorithm by simply performing all the tests without regard to their outcome, ${\displaystyle t(d,n)\leq {\bar {t}}(d,n)}$. Finally, when ${\displaystyle 0\neq d\neq n}$, there is at least one item whose defectiveness must be determined (by at least one test), and so ${\di$$splaystyle 1\leq t(d,n)}$.

요약하면($0{\displaystyle \mathrm{}}$ ${\displaystyle \ne }$ ${\displaystyle d}$ ${\displaystyle \ne n}$ ${\displaystyle 0\neq$ d$\neq n}$을 가정할 때),$$ $1{\displaystyle \mathrm{}t}$ t${\displaystyle }$(${\displaystyle d,}$ ${\displaystyle n}$)${\displaystyle t}$ t${\displaystyle \text{'}\text{'}\text{'}\text{'}\text{'}\text{'}\text{'}(d}$ ,${\displaystyle n}$ ) ${\displaystyle \le }$ n ${\displaystystyleq t(d,n)\bar{t}(d,n$^[f]$leq n}.$

정보 하한

$필요$한 시험 횟수의 하한은 S ${\$로 표시된 표본 공간의 개념을 사용하여 설명할 수 있으며, 이는 단순히 불량품의 가능한 배치의 집합이다$.$For any group testing problem with sample space ${\displaystyle {\mathcal {S}}}$ and any group-testing algorithm, it can be shown that ${\displaystyle t\geq \lceil \log _{2}{ {\mathcal {S}} }\rceil }$, where ${\displaystyle t}$ is the minimum number of tests required to identify all def오차 확률이 0인 경우이것을 하한정보라고 한다.^[3]이 경계는 각 시험 후 $S{\displaystyle \mathcal{}}$ ${\$이(가) 두 개의 분리 하위 집합으로 나뉘며$$, 각각은 시험의 가능한 두 결과 중 하나에 해당한다는 사실에서 도출된다.

그러나 하한선 정보 자체는 작은 문제라도 대개는 달성할 수 없다.^[3]$이$는 S ${\$의 분할이 임의적인 것이$$ 아니기 때문이다.

실제로 하한 정보는 알고리즘이 오류를 범할 가능성이 0이 아닌 경우에 일반화할 수 있다.이 형식에서 정리는 우리에게 시험 횟수에 근거한 성공 확률에 대한 상한을 준다.For any group-testing algorithm that performs ${\displaystyle t}$ tests, the probability of success, ${\displaystyle \mathbb {P} ({\textrm {success}})}$, satisfies ${\displaystyle \mathbb {P} ({\textrm {success}})\leq t/\log _{2}{n \choose d}}$.이것을 강화시킬 수 있다: $P{\displaystyle \mathbb{}}$(${\displaystyle \text{성공}}$) ${\displaystyle \le }$ 2 ${\displaystyle \frac{t^{}}{}}$ ${\displaystyle \frac{{}^{}}{\genfrac{}{}{0ex}{}{n}{}}}$ d$){\$ {$2^{t}{n \n$ 선택 d$\}).$^[5][20]

비적응 알고리즘의 표현

비적응 그룹 시험을 위한 알고리즘은 두 개의 뚜렷한 단계로 구성된다.첫째, 각 시험마다 몇 개의 시험을 수행할지, 어떤 항목을 포함시킬지 결정된다.흔히 디코딩 단계라고 불리는 2단계에서는 각 그룹 테스트의 결과를 분석하여 어떤 항목에 결함이 있을 가능성이 있는지를 결정한다.1단계는 보통 다음과 같이 매트릭스로 인코딩된다.^[5]

• $n$ ${\$$displaystyle$ $n$$}$ 항목에$$ 대한 비적응 그룹 테스트 절차가 일부 $t{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 0_{}}$ ${\$${1},$${t$$}$ $테스트$로${\displaystyle {}_{}{구성}_{}}$된다고 가정합시다$.$이 체계에 대한 테스트 $매트릭스$는 ${\displaystyle t}$× n ${\$$displaystyle$ t$\times n$$\}$ 이진$$ 매트릭스${\displaystyle {}_{}}$ $여기$서${\displaystyle }$(${\displaystyle M}$ $)$ i = 1 {\$displaystyle (M)_$${$$ij}=$$1}($$그리고$ 다른 ${\displaystyle {}_{}}$에는 0)이다$.$

Thus each column of ${\displaystyle M}$ represents an item and each row represents a test, with a ${\displaystyle 1}$ in the ${\displaystyle (i,j){\textrm {-th}}}$ entry indicating that the ${\displaystyle i{\textrm {-th}}}$ test included the ${\displaystyle j{\textrm {-th}}}$항목 및 다른$$ $항목$을 나타내는$$0 {\$displaystyle$ 0$}$

알 수 없는 불량 집합을 설명하는 $벡터{\displaystyle \mathbf{}}$ x ${\$길이 $n{\displaystyle }$ ${\displaystyle$ n$\})$뿐만 아니라, 각 테스트의 결과를 설명하는 결과 벡터를 도입하는 것이 일반적이다.

• $t{\displaystyle }$ ${\displaystyle t}$을(를) 비적응 알고리즘에 의해 수행된 테스트 횟수로$$ 한다.The result vector, ${\displaystyle \mathbf {y} =(y_{1},y_{2},\dots ,y_{t})}$, is a binary vector of length ${\displaystyle t}$ (that is, ${\displaystyle \mathbf {y} \in \{0,1\}^{t}}$) such that ${\displaystyle y_{i}=1}$ if and only if the result of $i{\displaystyle }$ ${\displaystyle \text{-th}}$ ${\$ 테스트가$$ 양수(즉, 하나 이상의 불량품이 포함됨)^[g]였습니다.

이러한 정의로 비적응 문제를 다음과 같이 재구성할 수 있다: 먼저 테스트 매트릭스를 $선택$하고 M ${\displaystyle$ M$}$을$($를) 선택한 후 벡터 $y{\displaystyle \mathbf{}}$ ${\$을(를) 반환한다.그러면 문제는 $y{\displaystyle \mathbf{}}$ ${\$를) 분석하여$$ $x{\displaystyle \mathbf{}}$ ${\$에 대한 추정치를 찾는 것이다$.$

그룹 테스트에서 오류가 발생할 확률이 일정한 가장 단순한 소음의 경우, $q{\displaystyle }$ ${\displaystyle q}$이(가$)$ 있는 경우, $임의$의 이진 벡터 v$${\$displaystyle \mathbf {v}$을(를) 고려한다$.$ 여기서 각 항목은 $1{\displaystyle \mathrm{}}$ ${\displaystystyle$ q$}$의 확률$$ $q {\$displaysty}이($으{\displaystyle \mathrm{}}$)이고$,$ 0 ${\displaystyplaystypute$)은 0이다.$스타일 0}$이(가) 아니면.The vector that is returned is then ${\displaystyle {\hat {\mathbf {y} }}=\mathbf {y} +\mathbf {v} }$, with the usual addition on ${\displaystyle (\mathbb {Z} /2\mathbb {Z} )^{n}}$ (equivalently this is the element-wise XOR operation).노이즈가 많은 알고리즘은 $y{\displaystyle \stackrel{}{\mathbf{}}}$ ${\$을(를) 사용하여$$ $x{\displaystyle \mathbf{}}$ ${\$를) 추정해야 한다($$$y{\displaystyle \mathbf{}}$ ${\$^[5]

비적응 알고리즘에 대한 경계

행렬 표현은 비적응 집단 시험에 대한 어느 정도 한계를 증명할 수 있게 한다.이 접근방식은 $d{\displaystyle }$ ${\displaystyle$d} -분리$$ 가능한 행렬을 고려하는 많은 결정론적 설계의 방식을 반영한다.^[3] 여기서 d {\displaystyle d$}).$

• $이진$ 행렬인 $M{\displaystyle }$ ${\$$displaystyle M}$은$$열 중 d {\displaystyle d}의 모든 부울 합(논리적 OR)이$구별$되는 경우$$d ${\displaystyle d}-$분리할 수 있는 $행렬$로 불린다.또한 $d{\displaystyle \stackrel{}{}}$ ${\$ -d}-분리$$ 가능한 표기법은 $M{\displaystyle }$ ${\displaystyle M}$의$$열 중 최대$$ $d{\displaystyle }$ ${\displaystyle d}$의 모든 합이 구별됨을 나타낸다(이는 $M{\displaystyle }$ ${\displaystyle$ $k}$ -d$}$의 $모든{\displaystyle }$ k${\displaystytyled$}과 동일하지 않음)..)

$M{\displaystyle }$ ${\displaystyle M}$이(가) 테스트$$ 매트릭스인 $경우{\displaystyle }$ d ${\displaystyle$ d$}$ -contractable$$$$($d)$의 속성은 $d{\displaystyle }$ ${\d$$}$까지 불량품을 구별할 수$있는$ 것과 동일하다$$.그러나 이것이 간단할 것이라고 보장하지는 않는다.$d{\displaystyle }$ ${\displaystyle d}$ -disjunctionity라고 불리는 더 강한 속성이 그렇다.

• $이진{\displaystyle }$ 행렬인 $M{\displaystyle }$ ${\displaystyle M}$은 d ${\displaystyle d}$ 열의$$ 부울 합계가 다른 열을 포함하지 않으면 $d{\displaystyle }$ ${\displaystyle$ d$}$ - disjunct라고 부른다$$.(이 맥락에서 B가 1을 갖는 모든 인덱스에 대해 A 열도 1을 갖는 경우 열 B를 포함한다고 한다.)

$d{\displaystyle }$ ${\displaystyle d}$ -분리 테스트$$ 매트릭스의 유용한 속성은 $최대{\displaystyle }$ d ${\displaystyle d}$개의$$ 불량품일 경우 모든 비불량 품목이 결과가 음수인 적어도 하나의 테스트에 나타난다는 것이다.이것은 불량품을 찾는 간단한 절차가 있다는 것을 의미한다: 단지 음성 테스트에 나타나는 모든 품목을 제거하라.

$d{\displaystyle }$ ${\$$displaystyle d}$ $-separable$ 및 d {\$displaystyle$ d$}$ -disjection$$ 행렬의 속성을 사용하면 n {\$displaystyle n}$개$$ 총 항목 중 $d{\displaystyle }$ ${\displaystyle d}$ 불량품을$$ 식별하는 문제에 대해 다음을 표시할 수 있다.^[4]

1. $O{\displaystyle (d}$ ${\displaystyle {\log }_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ $){\displaystyle O(d\log _{2}n)}$ 로서 점증적으로 작은 평균 오차 확률을 위해 필요한 테스트 수입니다$.$
2. $O{\displaystyle }$(d ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {\log }_{}}$ ${\displaystyle 2}$probabilityn ) ${\displaystyle O(d^{2}\log _{2}n)}$ 로서 오류 척도의 점증적으로 작은 최대 확률에 필요한 테스트 수입니다$.$
3. $O{\displaystyle }$(d 2 ${\displaystyle \frac{{\log }_{}}{}}$ ${\displaystyle \frac{{2\mathrm{}}_{}}{}}$ ${\displaystyle d\frac{{}^{}}{}}$ ${\displaystyle \frac{{n\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{\log }_{}}{}}$ 2 ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{d}{}}$)${\$ O$\left({\frac {d^{2}\log$ _${2}n$}{\$log _{2}d}\right)$로 오류 척도의 제로 확률을 위해 필요한 테스트 수입니다$.$

일반화된 이항 분할 알고리즘

일반화된 이항 분할 알고리즘은 다음과 같이 $n{\displaystyle }$ ${\displaystyle n}$개 항목$$ 중에서 $d{\displaystyle }$ ${\displaystyle d}$개$$ 이하의 불량품을 찾아내는 본질적으로 최적의 적응형 그룹 테스트 알고리즘이다.^[3][14]

1. $n{\displaystyle }$ ${\displaystyle \le }$ ${\displaystyle 2}$ ${\displaystyle d}$- ${\displaystyle 2}$ ${\displaystyle n\leq 2d-2}$인 경우$$$n{\displaystyle }$ ${\displaystyle n}$ 항목을$$ 개별적으로 테스트하십시오.그렇지 않으면 ${\displaystyle l}$= ${\displaystyle \mathrm{n}}$- ${\displaystyle d}$+ 1 ${\dplaystyle l=n-d+1}$및$$ $\alpha {\displaystyle }$=${\displaystyle }$α = ⌊ ${\displaystyle 로그}$ ${\displaystyle {2\mathrm{}}_{}\rfloor }$ ${\displaystyle l}$ / d$display$ {\d디스플레이 스타일 $\alpha =\lfloor \log }{2}{l/d}\rfloor }$를 설정하십시오$.$
2. 크기 ${\displaystyle {2\alpha }^{}}$ ${\$ 그룹의 그룹을 테스트한다$.$ 결과가 음수이면 그룹의 모든 항목이 비결함으로 선언된다. $n{\displaystyle }$ ${\displaystyle :=}$ ${\displaystyle n}$ -${\displaystyle {\mathrm{}}^{}}$ ${\displaystyle {\alpha }^{}}$ ${\$을 설정하고$$ 1단계로 이동한다.그렇지 않으면 이진 검색을 사용하여 결점이 없는 $항목$의 x {\$displaystyle x}$과$($와) 불특정 다수를 식별하고 $n{\displaystyle }$ ${\displaystyle :=}$ n${\displaystyle }$- ${\displaystyle 1}$- ${\displaystyle x}$ ${\displaystyle$ n$:=n-1-x}$ $및$ d ${\displaystyle :=}$ d${\displaystyle }$- ${\displaystyle 1}$ ${\displaystyle d:=d-1}$을$($를)로 설정하십시오. 1단계로 이동하십시오.

The generalised binary-splitting algorithm requires no more than ${\displaystyle T}$ tests where ${\displaystyle T={\begin{cases}n&n\leq 2d-2\\(\alpha +2)d+p-1&n\geq 2d-1\end{cases}}}$.^[3]

들어 n/d{\displaystyle n/d} 큰, Td로그는 호평 t과 비교할 만한 2⁡(n/d){\displaystyle T\rightarrow d\log_{2}(n/d)},[3])e로그 → 보여 줄 2⁡ ed로그 2⁡(nd){\displaystyle t={\frac{e}{\log_{2}e}}d\log _ᆱ\left({\frac{n}{d}}\right)}시험 Li'에 필요하다.s${\displaystyle s}$ $[\displaystyle s}$ - 단계$$ 알고리즘.실제로 일반화된 이항 분할 알고리즘은 다음과 같은 의미에서 최적화에 가깝다.When ${\displaystyle d\geq 2}$ it can be shown that ${\displaystyle T-B_{I}(d,n)\leq (d-1)}$, where ${\displaystyle B_{I}(d,n)=\left\lceil \log _{2}\sum _{i=0}^{d}{n \choose i}\right\rceil }$ is the information lower묶인^[3][14]

비적응 알고리즘

비적응적 그룹 시험 알고리즘은 불량품의 수, 또는 적어도 불량품의 좋은 상한선이 알려져 있다고 가정하는 경향이 있다.^[5]이 수량은 이 절에서$$ $d{\displaystyle }$ ${\displaystyle d}$로 표시된다.한계를 알 수 없는 경우 $d{\displaystyle }$ ${\displaystyle$ d$}$을(를) 추정하는 데 도움이 될 수 있는 쿼리 복잡성이 낮은 비적응 알고리즘이 존재한다$.$^[21]

콤비네이터 직교 매칭 추적(COMP)

결합 직교 매칭 추적(COMP)은 이 절에서 따르는 보다 복잡한 알고리즘의 기초를 형성하는 단순한 비적응 집단 시험 알고리즘이다.

첫째, 시험 행렬의 각 항목은 확률 1${\displaystyle }$/ $d{\displaystyle \mathrm{}}$ ${\디스플레이$ 스타일 1/$d}$ 및 $그렇지$ 않은$$경우 0 {\$디스플레이$ 스타일 0}을$($를) 가진$$ $1{\displaystyle \mathrm{}}$ ${\디스플레이$ 스타일 $1}$이(가) 되도록 선택된다.

디코딩 단계는 열(즉, 항목별) 방식으로 진행된다.항목이 나타나는 모든 검사에서 양성이면 해당 항목은 불량으로 선언되고, 그렇지 않으면 해당 항목은 불량으로 간주된다.또는 동등하게, 결과가 음수인 검정에 항목이 나타나면 해당 항목은 불량으로 선언되고, 그렇지 않으면 불량으로 간주된다.$이{\displaystyle }$ 알고리즘의 중요한 속성은 M ${\displaystyle M}$의 j번째 열(비결함 항목 j에 해당하는)에 있는 위치가 결함 항목에 해당하는 다른 열의 열로 "숨겨져 있는" 경우 거짓 양성이 발생하지만 결코 거짓 음성을 생성하지 않는다는 것이다.

COMP 알고리즘은 오류 확률을 $n{\displaystyle {}^{}}$ -${\displaystyle {\Delta }^{}}$ ${\$$displaystyle ed(1+\delta )\ln(n)}$보다 작거나 같도록 $e{\displaystyle }$ - Δ {\$displaystyle$ n$^{-\delta }}$보다 작은 오류 확률을 가지기 위해 e ${\displaystyle d}$(${\displaystyle 1}$+ ${\displaystyle \Delta }$) ${\displaystyle \ln }$(${\displaystyle n)}$를 요구하지 않는다$.$^[5] 이는 위의 평균 오차 확률 하한 하한 계수 내에 있다.

소음이 심한 경우, $양성$ 항목에 해당하는 M ${\displaystyle M}$ 열의 위치 집합이 결과 벡터 내의 위치 집합에 완전히 포함되어야 한다는 원래 COMP 알고리즘의 요구사항을 완화한다.대신 일정 수의 "미스매치"를 허용한다. 이 불일치 수는 각 열의 미즈매치 수와 소음 매개변수 $q{\displaystyle }${\$displaystyle q}$에 따라 달라진다$.$ 이 소음 COMP $알고리즘$은${\displaystyle \mathrm{}}$4.$36$+${\displaystyle \sqrt{}1\sqrt{\mathrm{}}}$ +${\displaystyle {}^{}\sqrt{\Delta }}$ )${\displaystyle {}^{}{2\mathrm{}}^{}}$ (${\displaystyle 1}$ - ${\displaystyle 2{}^{}}$q${\displaystyle {}^{}}$) - ${\displaystyle {}^{}}$ d ${\displaystyle {\mathrm{로그}}_{}}$ ${\displaystyle 2}$ n$${\$displaystylease$ 4.36$({\$$sqrt$.$델타{}+{\sqrt{1+\n1}^{2}(-1-2q)^{-2}d\log _{2}{n}}$ 테스트하여$$ 최대 ${\$ n$^{-\message }}$에서 오류 확률을 달성하십시오$.$^[5]

확정불량품(DD)

확정결함수법(DD)은 잘못된 긍정을 제거하려는 COMP 알고리즘의 확장이다.DD에 대한 성능 보증은 COMP를 엄격히 초과하는 것으로 나타났다.^[19]

디코딩 단계는 COMP 알고리즘의 유용한 속성을 사용한다: COMP가 비결함을 선언하는 모든 항목은 확실히 결함이 없다(즉, 잘못된 부정은 없다).다음과 같이 진행된다.

1. 먼저 COMP 알고리즘이 실행되며, 검출된 모든 비결함은 제거된다.이제 남은 모든 품목은 "아마도 결함이 있을 것"이다.
2. 다음으로 알고리즘은 모든 양성 테스트를 살펴본다.만약 어떤 항목이 시험에서 유일한 "가능한 결함"으로 나타난다면, 그것은 반드시 결함이어야 하기 때문에 알고리즘은 그것을 결함이라고 선언한다.
3. 그 밖의 모든 항목은 비결함으로 가정한다.이 마지막 단계에 대한 정당성은 불량품의 수가 전체 항목 수보다 훨씬 적다는 가정에서 비롯된다.

1단계와 2단계는 절대 실수를 하지 않으므로 알고리즘은 결함이 있는 품목을 결함이 없는 것으로 선언하는 경우에만 실수를 할 수 있다는 점에 유의하십시오.따라서 DD 알고리즘은 거짓 음성만 생성할 수 있다.

순차 COMP(SCOMP)

SCOMP(Sequential COMP)는 DD가 마지막 단계까지 실수하지 않는다는 점을 활용한 알고리즘으로, 나머지 항목은 결함이 없는 것으로 가정한다.선언된 불량품 세트를 $K{\displaystyle }$ ${\$$displaystyle$ $K}$로 한다$.$ $포지티브{\displaystyle }$테스트는 K {\displaystyle $K}$에 적어도 하나의 품목이 포함된 경우$$ $K{\displaystyle }$ ${\displaystyle K}$에 의해 설명된다$.$ SCOMP의 주요 관찰 내용은 DD에 의해 발견된 불량품 세트가 모든 포지티브 테스트를 설명하지 않을 수 있으며, 설명되지 않은 모든 테스트는 반드시 이루어져야 함입니다.숨겨진 결점을 찌르다

알고리즘은 다음과 같이 진행한다.

1. DD 알고리즘의 1단계와 2단계를 수행하여 불량품 집합에 대한 초기 추정치인$$$K{\displaystyle }$ ${\displaystyle K}$을(를) 얻으십시오.
2. $K{\displaystyle }$ ${\displaystyle K}$이(가) 모든 양성 테스트를 설명하는$$ 경우 알고리즘을 종료하십시오. $K{\displaystyle }$ ${\displaystyle K}$은(는) 불량품 집합의 최종 추정치임.
3. 설명되지 않은 테스트가 있는 경우 설명되지 않은 테스트의 가장 많은 횟수에 나타나는 "잠재적인 결함"을 찾아 결함이 있다고 선언하십시오($즉{\displaystyle }$, 설정 K ${\displaystyle K}$에 추가).$$2단계로 이동하십시오.

시뮬레이션에서 SCOMP는 최적으로 거의 성능을 발휘하는 것으로 나타났다.^[19]

응용 프로그램 예

집단 검사 이론의 일반성은 그것을 클론 검사, 전기 반바지 찾기,^[3] 고속 컴퓨터 네트워크,^[22] 건강 검진, 수량 검색, 통계,^[16] 기계 학습, DNA 염기서열 분석,^[23] 암호 해독,^[24][25] 데이터 포렌식 등을 포함한 많은 다양한 응용 분야에 빌려준다.^[26]이 절에서는 이러한 애플리케이션의 소량 선택에 대한 간략한 개요를 제공한다.

멀티액세스 채널

멀티액세스 채널은 많은 사용자를 한 번에 연결하는 통신 채널이다.모든 사용자는 채널에서 청취와 전송이 가능하지만, 둘 이상의 사용자가 동시에 송신하면 신호가 충돌해, 알아들을 수 없는 노이즈로 줄어든다.멀티액세스 채널은 특히 무선 컴퓨터 네트워크와 전화 네트워크 등 다양한 실제 어플리케이션에 중요하다.^[27]

멀티액세스 채널의 두드러진 문제는 사용자들의 메시지가 충돌하지 않도록 사용자에게 전송 시간을 할당하는 방법이다.간단한 방법은 각 사용자에게 전송할 시간 간격을 부여하여 $n{\displaystyle }$ ${\displaystyle n}$ 슬롯을$$ 요구하는 것이다. (이를 시간 분할 멀티플렉싱 또는 TDM이라고 한다.) 그러나 이것은 메시지가 없을 수 있는 사용자에게 전송 슬롯을 할당하기 때문에 매우 비효율적이며, 일반적으로 소수의 사용자만 원하지 않을 것으로 가정한다.o 주어진 시간에 전송 – 그렇지 않으면, 처음부터 멀티액세스 채널은 실용적이지 않다.

집단 테스트의 맥락에서, 이 문제는 보통 다음과 같은 방법으로 시간을 'epochs'로 나누어 해결된다.^[3]사용자는 epoech의 시작에 메시지가 있으면 'active'라고 부른다.(epoech 중에 메시지가 생성되면 사용자는 다음 메시지가 시작될 때만 활성화된다.)모든 활성 사용자가 성공적으로 메시지를 전송했을 때 신기루가 끝난다.그 다음, 문제는 주어진 시대에서 모든 활성 사용자를 찾고, 그들이 전송할 시간을 예약하는 것이다. (아직 그렇게 성공적으로 완료하지 못한 경우)여기서 사용자 집합에 대한 테스트는 전송을 시도하는 사용자에 해당한다.테스트 결과는 활성 사용자가 없거나 정확히 한$$명의 활성 사용자($메시지$ 성공) $또는 한$명 ${\displaystyle \mathrm{이상}}$의 활성$$ $사용자{\displaystyle {\mathrm{}}^{(}}$메시지 충돌)에 해당하는 0, 1, {\디스플레이 스타일 0$,$1$,}$ 및 2 + ${\$ 스타일 $2^{+}}$ 전송을 시도한 사용자 $수입니다{\displaystyle \mathrm{}.}$따라서 결과가${\displaystyle }${${\displaystyle 0,}$ ${\displaystyle 1}$,${\displaystyle {\mathrm{}}^{}}$ +${\displaystyle {}^{}}$ ${\displaystyle \{0,1,2^{+}\}}}$인 적응형 그룹 테스트 알고리즘을 사용하여$$어느 사용자가 에폭에서 전송하기를 원하는지 결정할 수 있다.그런 다음, 아직 전송에 성공하지 못한 사용자는 이제 비활성 사용자에게 시간을 낭비하지 않고 전송할 슬롯을 할당할 수 있다.

기계 학습 및 압축 감지

머신러닝(machine learning)은 DNA 분류, 사기 탐지, 표적 광고 등 소프트웨어 응용 분야가 많은 컴퓨터 과학 분야다.머신러닝의 주요 하위 분야 중 하나는 '예에 의한 학습' 문제인데, 여기서 과제는 특정 지점의 값을 부여했을 때 알 수 없는 기능의 근사치를 구하는 것이다.^[3]이 절에서 설명한 바와 같이, 이 기능 학습 문제는 그룹 테스트 접근방식으로 다루어질 수 있다.

In a simple version of the problem, there is some unknown function, ${\displaystyle f:\{0,1\}^{N}\to \{0,1\}}$ where ${\displaystyle f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}}$, and ${\displaystyle {\textbf {a}}\in \{0,1\}^{N}}$ (using logical 산술: 덧셈은 논리적 OR이고 곱셈은 논리적 AND).여기서 ${\$은(는) '${\displaystyle }$ ${\displaystyle$ d$}$ spars$$'이며$$, 이는 최대 $d{\displaystyle }$ ${\displaystyle \ll }$ ${\displaystyle N}$ ${\displaystyle d\ll N}$ 항목이$$ 1 ${\displaystystyle$ 1$\}$$임$을 의미한다.목표는{\displaystyle f}이 t{\displaystyle지}를 가능한 한 작다 t{\displaystyle지}점 평가를 사용하여 f에 대한 근사치를 세우는 것이다.반면 f{\displaystyle f}알고리즘에 의해 잡는다[4]( 맞아 회복하고 f{\displaystyle f}제로 오류 알고리즘에, n.다 해당합니다오차 확률이 0인 경우).

In this problem, recovering ${\displaystyle f}$ is equivalent to finding ${\displaystyle {\textbf {a}}}$. Moreover, ${\displaystyle f({\textbf {p}})=1}$ if and only if there is some index, ${\displaystyle n}$, where ${\displaystyle {\textbf {a}}_{n}={\textbf {p}}_{$$n1}=1$따라서 이 문제는 $d{\displaystyle }$ ${\displaystyle d}$개의$$ 불량품 및 $n{\displaystyle }$ ${\displaystyle n}$개의$$ 총 품목에 대한 그룹 테스트 문제와 유사하다.${\$의 항목은 불량품이며$$, $1{\displaystyle }$ ${\displaystyle 1$ p ${\${$p$$}}$이(${\displaystyle 가}$) 테스트를$$ 지정하고, f${\displaystyle (}가{\displaystyle )}$= ${\displaystyle 1}$ ${\displaystyf{p}=1}$인 경우에만 양성이다$.$^[4]

In reality, one will often be interested in functions that are more complicated, such as ${\displaystyle f:\mathbb {C} ^{N}\to \mathbb {C} }$, again where ${\displaystyle f({\textbf {x}})={\textbf {a}}\cdot {\textbf {x}}}$. Compressed sensing, which is closely related to group testing, can이 문제를 해결하는 ^[4]데 이용되다

압축 센싱에서 목표는 $v{\displaystyle }$measurements ${\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$ 신호를 여러 가지 측정을 통해 재구성하는 것이다.이러한 측정은 $선택$된 벡터로$$ v ${\$의 도트 곱을 취한 것으로 모델링된다.^[h]목적은 적은 수의 측정을 사용하는 것이지만, 신호에 대해 어떤 것이 가정되지 않는 한 이것은 일반적으로 불가능하다.$이러한{\displaystyle }$ 가정 중 하나는 v^[30][31] ${\$의 소수 항목만 유의하다는 것으로, 이는 크기가 크다는 것을 의미한다.측정값이 $v{\displaystyle }$ ${\${$v$$\}\}$의 도트 제품이기 때문에 M ${\displaystyle v}$= ${\displaystyle q}$ = q ${\$ M${v}={\$$displaystyle M}$은(는$)$ $t{\displaystyle }$ ${\displaystyle \times }$ N ${\$$displaystystyle$ $t\times N}$ 행렬로$$ 선택$$ 및 $\$$yle \mathbf {q}$은$($는) 측정 결과 집합이다.이 구조는 압축 감지가 일종의 '연속적인' 집단 시험이라는 것을 보여준다.

압축 감지의 일차적인 어려움은 어떤 항목이 중요한지 확인하는 것이다.^[30]일단 그렇게 되면, 출품작의 실제 값을 추정할 수 있는 다양한 방법이 있다.^[32]이 식별 작업은 그룹 테스트의 간단한 적용으로 접근할 수 있다.여기에서 그룹 테스트는 복잡한 숫자로 테스트되는 항목의 합을 산출한다.시험 결과가 크기가 큰 복잡한 숫자를 생성하는 경우 양수라고 하며, 이는 유의한 항목이 희박하다는 가정을 고려할 때 적어도 하나의 유의한 입력이 시험에 포함되어 있음을 나타낸다.

이러한 유형의 결합 검색 알고리즘에는 d ${\displaystyle {\mathrm{}}^{({\mathrm{로그}}_{}}}$ ${\displaystyle {{2\mathrm{}}_{}}^{}}$ ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {{\mathrm{로그}}_{}}^{}}$ ${\displaystyle {{2\mathrm{}}_{}}^{}}$ ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {N{}^{}}^{}}$) O${\displaystyle {{}^{}}^{}}$( ${\displaystyle {1^{}}^{}}$) ${\$ 측정을$$ 요구하는 명시적 결정론적 구조가 있다.^[33]그러나 그룹 테스트와 마찬가지로 이러한 구성들은 하위 최적이며, 임의 구성(예: COMP)은 $종종{\displaystyle }$ N ${\displaystyle N}$에서 $하위$ 선형으로$$f {\$displaystyle f}$을(를) 복구할 수 있다$.$^[32]

COVID19 시험을 위한 멀티플렉스 검사 설계

2020년 COVID-19와 같은 전염병 동안, 바이러스 검출 검사는 때때로 비적응적 그룹 시험 설계를 사용하여 실행된다.^[34][35]한 예는 실험실 표준 96 웰 플레이트에서 실행할 오픈 소스 그룹 시험 설계를 발표한 Orgami Assays 프로젝트에서 제공되었다.^[36]

실험실 환경에서, 그룹 시험의 한 가지 어려움은 혼합물을 만드는 데 시간이 많이 걸리고 손으로 정확히 하기 어렵다는 것이다.종이접기 검사는 정비사가 환자 샘플을 테스트 웰에 할당하는 방법을 안내하는 종이 템플릿을 제공하여 이 시공 문제에 대한 해결 방법을 제공했다.^[37]

가장 큰 그룹 테스트 설계(XL3)를 사용하여 94개의 검사 웰에서 1120개의 환자 샘플을 테스트할 수 있었다.실제 양성률이 충분히 낮으면 추가 검사가 필요하지 않았다.

데이터 포렌식

데이터 포렌식이란 범죄의 디지털 증거를 수집하는 방법을 찾는 데 전념하는 분야다.그러한 범죄에는 일반적으로 피해자의 데이터, 문서 또는 데이터베이스를 수정한 상대자가 관련되는데, 여기에는 세금 기록의 변경, 그 존재를 숨기는 바이러스, 개인 데이터를 수정한 신원 도적이 포함된다.^[26]

데이터 포렌식에서 공통적인 도구는 단방향 암호해시다.이것은 데이터를 가져가는 함수로서, 역행하기 어려운 절차를 통해 해시라는 고유 숫자를 만들어 낸다.^[i]종종 데이터보다 훨씬 짧은 해시는 정보의 전체 복사본을 낭비 없이 저장할 필요 없이 데이터가 변경되었는지 확인할 수 있게 해준다: 현재 데이터에 대한 해시를 과거 해시와 비교하여 변경 사항이 발생했는지 확인할 수 있다.이 방법의 불행한 속성은 데이터가 수정되었는지 여부를 쉽게 알 수 있지만, 그 방법을 결정할 방법이 없다는 것이다. 즉, 데이터의 어느 부분이 변경되었는지 복구하는 것은 불가능하다.^[26]

이러한 한계를 극복하는 한 가지 방법은 데이터 구조의 하위 집합인 해시를 더 많이 저장하여 공격이 발생한 지점을 좁히는 것이다.그러나 순진한 접근법으로 공격의 정확한 위치를 찾으려면 구조물의 모든 기준점에 대해 해시를 저장해야 할 것이며, 이는 애초에 해시의 포인트를 무찌를 수 있다.(일부 자료의 정규 사본을 저장하는 편이 나을지도 모른다)그룹 테스트는 저장해야 하는 해시의 수를 극적으로 줄이는 데 사용될 수 있다.테스트는 저장된 해시와 현재 해시의 비교가 되며, 불일치가 있을 때 양성이 된다.이는 현재 해시를 생성한 그룹에 적어도 하나 이상의 편집된 기준점(이 모델에서 결함으로 간주됨)이 포함되어 있음을 나타낸다.^[26]

실제로 필요한 해시의 양은 너무 적어 해시들이 참조하는 테스트 매트릭스와 함께 데이터 자체의 조직 구조 내에 저장될 수도 있다.이는 메모리에 관한 한 '무료'로 시험을 실시할 수 있다는 것을 의미한다.(해싱 함수를 비밀리에 결정하는 데 사용되는 마스터키/암호를 제외하고 그렇다)^[26]

메모들

참조

인용구

일반참조

• Ding-Zhu, Du; Hwang, Frank K. (1993). Combinatorial group testing and its applications. Singapore: World Scientific. ISBN 978-9810212933.
• Atri Rudra의 오류 수정 코드: 조합, 알고리즘 및 응용 프로그램(2007년 봄), 7강.
• 아트리 루드라의 오류 수정 코드에 관한 과정: 조합론, 알고리즘, 응용 프로그램(2010년 봄), 강의 10, 11, 28, 29
• 듀, 디, 앤 황, 에프. (2006)설계 풀링 및 비적응 그룹 테스트.보스턴:Twayne Publishers.
• Aldridge, M, Johnson, O. and Scarlett, J.(2019), 그룹 테스트: 정보이론의 관점, 통신과 정보이론의 기초와 동향: 제15권: 제3-4, 페이지 196–392. 도이:10.1561/0100000099
• Ely Porat, Amir Rothchild: 명시적 비적응적 결합 집단 시험 체계.ICALP (1) 2008: 748-759
• Kagan, Eugene; Ben-gal, Irad (2014), "A group testing algorithm with online informational learning", IIE Transactions, 46 (2): 164–184, doi:10.1080/0740817X.2013.803639, ISSN 0740-817X

참고 항목

• 밸런스 퍼즐