저밀도 패리티 체크코드

정보 이론에서 저밀도 패리티 체크(LDPC) 코드는 노이즈가 많은 전송 채널을 ^[1][2]통해 메시지를 전송하는 방법인 선형 오류 수정 코드입니다.LDPC는 스파스 태너 그래프(양분 ^[3]그래프의 서브클래스)를 사용하여 구축됩니다.LDPC 코드는 캐퍼시티 어프로치 코드입니다.즉, 노이즈 임계값을 대칭 메모리리스 채널의 이론상 최대값(섀넌 한계)에 매우 가깝게 설정할 수 있는 실용적인 구조가 존재합니다.노이즈 임계값은 채널노이즈의 상한을 정의합니다.이 상한을 정의하면 정보가 손실될 확률을 원하는 만큼 줄일 수 있습니다.반복적인 신뢰 전파 기술을 사용하여 LDPC 코드를 블록 길이에 선형으로 시간적으로 디코딩할 수 있습니다.

LDPC 코드는 대역폭 제한 링크 또는 리턴 채널 제한 링크를 통한 신뢰성 있고 효율적인 정보 전송을 필요로 하는 어플리케이션에서 노이즈가 파손된 상황에서 점점 더 많이 사용되고 있습니다.LDPC 코드의 실장은 다른 코드(특히 터보 코드)에 비해 늦어지고 있습니다.터보 코드의 기본 특허는 2013년 ^[4][5]8월 29일에 만료되었습니다.

LDPC 코드는 1960년 ^[6][7]매사추세츠공과대학 박사학위 논문에서 LDPC 개념을 개발한 로버트 G. 갤러거를 기리기 위해 갤러거 코드로도 알려져 있다.LDPC 코드도 이상적인 조합 속성을 가지고 있는 것으로 나타났습니다.Galager는 논문에서 LDPC 부호가 높은 확률로 이진수 필드의 선형 부호에 대한 길버트-바르샤모프 경계를 달성한다는 것을 보여주었다.2020년에는 갤러거의 LDPC 코드가 목록 디코딩 용량을 달성하고 일반 필드의 선형 코드에 대한 Gilbert-Varshamov 경계를 달성하는 것으로 나타났다.^[8]

역사

1963년 ^[9]갤러거에 의해 처음 개발되었을 때 실행이 불가능했던 ^[10]LDPC 코드는 1996년 그의 작품이 재발견될 때까지 잊혀졌다.1993년에 발견된 용량 접근 코드의 또 다른 클래스인 터보 코드는 1990년대 후반에 딥 스페이스 네트워크 및 위성 통신과 같은 애플리케이션에 사용되는 부호화 체계가 되었습니다.그러나 저밀도 패리티 체크코드의 진보로 인해 에러 플로어 및 높은 코드 레이트 범위에서 성능 면에서 터보 코드를 능가하고 있어 터보 코드는 낮은 코드 레이트에만 적합합니다.^[11]

적용들

2003년, ^[12]디지털 텔레비전의 새로운 DVB-S2 규격에서는, 불규칙한 반복 축적(IRA) 스타일의 LDPC 코드가 6개의 터보 코드를 누르고, 에러 수정 코드가 되었습니다.DVB-S2 선정 위원회는 병렬 디코더 아키텍처가 아닌 효율성이 훨씬 낮은 시리얼 디코더 아키텍처를 사용하여 터보 코드 제안의 디코더 복잡성을 추정했습니다.이로 인해 터보 코드프로포절에서는 프레임사이즈가 LDPC 프로포절의 절반 정도로 사용됩니다.

2008년 LDPC는 ITU-T ^[13]G.hn 표준의 Forward Error Correction(FEC; 전송 오류 정정) 시스템으로서 컨볼루션터보 코드를 제패했습니다.G.hn는 디코딩 복잡도가 낮고(특히 1.0 Gbit/s에 가까운 데이터 레이트로 동작하는 경우), 제안된 터보 코드가 원하는 ^[14]동작 범위에서 중대한 에러 플로어를 나타냈기 때문에 터보 코드보다 LDPC 코드를 선택했습니다.

LDPC 코드는 10GBASE-T 이더넷에도 사용됩니다.이 이더넷은 트위스트 페어 케이블을 통해 초당 10기가비트 속도로 데이터를 전송합니다.2009년 현재 LDPC 코드는 하이 스루풋(HT) PHY ^[15]사양에서 802.11n 및 802.11ac의 옵션 부분으로서 Wi-Fi 802.11 규격의 일부이기도 합니다.LDPC는 802.11ax(Wi-Fi 6)^[16]의 필수 부분입니다.

일부 OFDM 시스템에서는 낮은 비트 오류율에서도 LDPC 수정 내부 코드를 통과하는 간혹 발생하는 오류('에러 플로어')를 수정하는 추가 외부 오류 수정이 추가되어 있습니다.예를 들어 다음과 같습니다.LDPC Coded Modulation(RS-LCM; 코드 변조)을 사용하는 리드 Solomon 코드는 리드 Solomon 외부 ^[17]코드를 사용합니다.DVB-S2, DVB-T2 및 DVB-C2 규격은 모두 BCH 코드 외부 코드를 사용하여 LDPC ^[18]디코딩 후 잔류 오류를 소거합니다.

5G NR은 제어채널에 폴라코드를, 데이터 ^[19][20]채널에는 LDPC를 사용합니다.

많은 TLC(및 그 이후) SSD가 LDPC 코드를 사용하고 있습니다.

운용상의 용도

LDPC 코드는 기능적으로 스파스 패리티 체크 매트릭스에 의해 정의됩니다.이 스파스 매트릭스는 종종 랜덤으로 생성되며, 희소성 제약조건에 따릅니다.LDPC 코드 구축에 대해서는 나중에 설명하겠습니다.이 코드들은 1960년 ^[7]로버트 갤러거에 의해 처음 고안되었다.

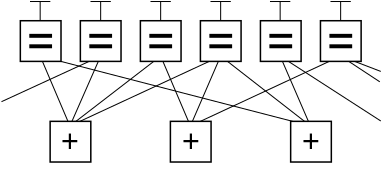
다음은 Forney의 계수 그래프 표기법을 사용한 LDPC 코드 예제 그래프 조각입니다.이 그래프에서는 그래프 상단의 n개의 변수 노드가 그래프 하단의 (n-k) 제약조건 노드에 연결되어 있습니다.

이것은 (n, k) LDPC 코드를 그래픽으로 표현하는 일반적인 방법입니다.유효한 메시지의 비트는 그래프 상단의 T에 배치되어 있으면 그래픽 제약 조건을 충족합니다.특히 변수 노드에 연결되는 모든 라인('=' 기호가 있는 상자)은 동일한 값을 가지며, 요인 노드('+' 기호가 있는 상자)에 연결되는 모든 값은 모듈로 2에서 0까지 합해야 합니다(즉, 짝수로 합해야 합니다).

화면 밖으로 나가는 행을 무시하면 유효한 코드워드에 대응하는6비트 문자열이 8개 있습니다(즉 0000001, 011001, 1100101, 001110, 010111).이 LDPC 코드 fragment는 6비트로 인코딩된3비트 메시지를 나타냅니다.여기서는 채널오류로부터의 회복 가능성을 높이기 위해 용장성이 사용됩니다.이것은 n = 6 및 k = 3인 (6, 3) 선형 코드입니다.

이 그래프 조각을 나타내는 패리티 체크 매트릭스는 그림 밖으로 나가는 선을 무시합니다.

$({displaystyle \mathbf {H} = pmatrix 1&1&1&0\\0&1&1&1&1\end{pmatrix} )}$

이 매트릭스에서 각 행은 3개의 패리티 체크 제약 조건 중 하나를 나타내며 각 열은 수신된 코드 워드의 6비트 중 하나를 나타냅니다.

이 예에서는 패리티 체크 매트릭스H를 GF(2)의 기본행 연산을 통해 ${\displaystyle \begin{array}{c}[-P{}^{}{}_{}\end{array}}$ T ${\displaystyle \begin{array}{c}{I}_{}\end{array}}$n${\displaystyle \begin{array}{c}{}_{}\end{array}}$- $](\displaystyle\begin${bmatrix$}-P^{T}) I_{n-k}\end{bmatrix})$ 형식으로$$ 하면 8개의 코드워드를 얻을 수 있습니다.

$={\begin{pmatrix}1&, 1&, 1&, 1&, 0&, 0\\0&, 0&, 1&, 1&, 0&, 1\\1&, 0&, 0&, 1&, 1&, 0\\\end{pmatrix}}_{1}\sim{\begin{pmatrix}1&, 1&, 1&, 1&, 0&, 0\\0&, 0&, 1&, 1&, 0&, 1\\0&, 1&, 1&, 0&, 1&, 0\\\end{pmatrix}}_{2}\sim{\begin{pmatrix}1&, 1&, 1&, 1&, 0&,{\displaystyle \mathbf{H}.0\\0&, 1&, 1&, 0&, 1&, 0\\0&, 0&, 1&, 1&, 0&, 1\\\end{pmatrix}}_{3}\sim{\begin{pmatrix}1&, 1&, 1&, 1&, 0&, 0\\0&, 1&, 1&, 0&, 1&, 0\\1&, 1&, 0&, 0&, 0&, 1\\\end{pmatrix}}_{4}.}$

스텝 1: H.

순서 2: 행 1을 행 3에 추가합니다.

순서 3: 행 2와 행 3을 바꿉니다.

스텝 4: 행 1을 행 3에 추가합니다.

여기서 제너레이터 매트릭스 G는 [${\displaystyle \begin{array}{c}Ik{}_{}\end{array}}$ P$]$ {$displaystyle {bmatrix}$ {$begin${bmatrix$\}{\displaystyle }$ 로 얻을 수 있습니다.$I_{k} P\end{bmatrix}}($특별한 경우 이진 $코드{\displaystyle }$ P $=$ -$$({$displaystyle$ P=-$P})$ 또는 구체적으로 다음과 같습니다.

$({displaystyle \mathbf {G} = pmatrix 1&0&1&1&1&1\\0&1&1&1\end{pmatrix})}$

마지막으로 가능한 8개의 3비트 문자열 모두에 G를 곱함으로써 8개의 유효한 코드워드를 얻는다.예를 들어 비트 문자열 '101'의 코드워드는 다음과 같이 얻을 수 있습니다.

(101)⊙(100101010111001110))(101011){\displaystyle{\begin{pmatrix}1&, 0&, 1\\\end{pmatrix}}\odot{\begin{pmatrix}1&, 0&, 0&, 1&, 0&, 1\\0&, 1&, 0&, 1&, 1&, 1\\0&, 0&, 1&, 1&, 1&, 0\\\end{pmatri.x}}={\begin{pmatrix}1&, 0&, 1&, 0&, 1&, 1\\\end{pmatrix}}},

여기서 $⊙(\displaystyle \odot)$은 mod 2 곱셈의 기호입니다.

점검 결과, G의 행 ${\displaystyle {공간}^{}}$은 ${\displaystyle {}^{}}$ = H ${\displaystyle \mathrm{T}}$ 0 \ $displaystyle$G \ $odot$ H$^{$$가{\displaystyle }$ 되도록 H와 직교한다.$T}=0}$

비트 문자열 '101'은 코드워드 '101011'의 첫 번째 3비트로 에 있습니다.

인코더 예시

그림 1은 대부분의 LDPC 인코더의 기능 컴포넌트를 나타내고 있습니다.

프레임의 부호화중에, 입력 데이터 비트(D)를 반복해, 구성 인코더 세트로 분배한다.구성 인코더는 일반적으로 어큐뮬레이터이며 각 어큐뮬레이터는 패리티 기호를 생성하는 데 사용됩니다.원래의 데이터(S_0,K-1)의 1 카피를 패리티 비트(P)와 함께 송신해, 코드 심볼을 구성한다.각 구성 인코더로부터의S 비트는 폐기됩니다.

패리티 비트는 다른 구성 코드 내에서 사용할 수 있습니다.

DVB-S2 레이트 2/3 코드를 사용하는 예에서 부호화된 블록 사이즈는 43200 데이터 비트(K=43200) 및 21600 패리티 비트(M=21600)를 포함한 64800 심볼(N=64800)입니다.각 구성 코드(체크 노드)는 8 데이터 비트를 부호화하는 제1 패리티 비트를 제외한 16 데이터 비트를 부호화한다.첫 번째 4680 데이터 비트는 13회(13개의 패리티 코드로 사용) 반복되며 나머지 데이터 비트는 3개의 패리티 코드(불규칙 LDPC 코드)로 사용됩니다.

비교를 위해 클래식 터보 코드는 일반적으로 병렬로 구성된2개의 구성 코드를 사용합니다.각 구성 코드는 데이터 비트의 입력 블록(K) 전체를 인코딩합니다.이러한 구성 인코더는 프레임의 1개의 복사본을 인터리브하는 코드인터리버에 의해 분리된 중간 깊이(8 또는 16 상태)의 재귀 컨볼루션코드(RSC)입니다.

반면 LDPC 코드에서는 다수의 Low Depth 구성 코드(어큐뮬레이터)가 병렬로 사용되며 각 코드는 입력 프레임의 극히 일부만 인코딩됩니다.많은 구성 코드는 반복 및 분배 연산을 통해 연결된 낮은 깊이(2 상태)의 '컨볼루션 코드'로 볼 수 있다.반복 및 분배 작업은 터보 코드에서 인터리버의 기능을 수행합니다.

다양한 구성 코드의 접속과 각 입력 비트의 용장성 수준을 보다 정확하게 관리할 수 있기 때문에 LDPC 코드 설계에 유연성이 높아져 경우에 따라서는 터보 코드보다 퍼포먼스가 향상될 수 있습니다.터보 코드는 낮은 코드환율에서도 여전히 LDPC보다 성능이 우수하거나 적어도 터보 코드의 경우 성능이 뛰어난 낮은 코드 설계가 더 쉬워 보입니다.

실제로 어큐뮬레이터를 구성하는 하드웨어는 부호화 프로세스 중에 재사용됩니다.즉, 패리티 비트의 첫 번째 세트가 생성되고 패리티 비트가 저장되면 다음 패리티 비트세트를 생성하기 위해 동일한 어큐뮬레이터 하드웨어가 사용됩니다.

디코딩

다른 코드와 마찬가지로 바이너리 대칭 채널 상의 LDPC 코드의 최대우도 디코딩은 NP-완전 문제입니다.유용한 크기의 NP-완전 코드에 대해 최적의 디코딩을 수행하는 것은 실용적이지 않습니다.

그러나 반복적인 믿음 전파 복호화에 기초한 차선의 기법은 우수한 결과를 제공하며 실질적으로 구현될 수 있다.차선의 디코딩 기법에서는 LDPC를 구성하는 각 패리티 체크를 독립 싱글 패리티 체크(SPC) 코드로 표시합니다.패리티 체크) 코드로 표시합니다.각 SPC 코드는 SOVA, BCJR, MAP 등의 Soft-In-Soft-out(SISO; 소프트인아웃) 기술을 사용하여 개별적으로 디코딩된다.각 SISO 디코딩의 소프트 결정 정보는 동일한 정보 비트의 다른 용장 SPC 디코딩과 상호 체크되고 업데이트됩니다.다음으로 갱신된 소프트 결정 정보를 사용하여 각 SPC 코드를 다시 디코딩한다.이 프로세스는 유효한 코드 워드에 도달하거나 디코딩이 모두 완료될 때까지 반복됩니다.이러한 유형의 디코딩은 종종 총곱 디코딩이라고 합니다.

SPC 코드의 디코딩은 종종 "체크 노드" 처리라고 불리며 변수의 크로스 체크는 종종 "변수 노드" 처리라고 불립니다.

실용적인 LDPC 디코더 실장에서는 SPC 코드 세트를 병렬로 디코딩하여 throughput을 높인다.

이와는 대조적으로, 2진수 삭제 채널에서의 믿음 전파는 반복적인 제약 만족으로 구성된 경우 특히 단순하다.

예를 들어, 위의 예에서 유효한 코드워드 101011이 바이너리 소거 채널을 통해 전송되고 첫 번째와 네 번째 비트가 지워진 상태에서 수신되어 ?01?11이 생성된다고 가정합니다.전송된 메시지는 코드 제약 조건을 만족해야 하므로 수신된 메시지를 팩트 상단에 적음으로써 나타낼 수 있습니다.또는 그래프를 표시합니다.

이 예에서는 첫 번째 비트에 연결된 모든 제약조건에 둘 이상의 알 수 없는 비트가 있기 때문에 아직 첫 번째 비트를 복구할 수 없습니다.메시지 디코딩을 계속하려면 지워진 비트 중 하나만 연결하는 제약 조건을 식별해야 합니다.이 예에서는 두 번째 제약 조건만 충족됩니다.두 번째 구속조건을 조사할 때, 네 번째 비트는 0이어야 합니다. 왜냐하면 그 위치의 0만이 제약을 충족하기 때문입니다.

그 후, 이 순서를 반복합니다.이제 네 번째 비트의 새 값을 첫 번째 제약 조건과 함께 사용하여 다음과 같이 첫 번째 비트를 복구할 수 있습니다.즉, 첫 번째 비트는 맨 왼쪽의 제약을 만족시키기 위한 비트여야 합니다.

따라서 메시지를 반복적으로 디코딩할 수 있습니다.다른 채널 모델의 경우 가변 노드와 체크 노드 간에 전달되는 메시지는 신뢰의 확률과 가능성을 나타내는 실수입니다.

이 결과는 수정된 코드워드 r에 패리티 체크 매트릭스H를 곱함으로써 검증할 수 있습니다.

$\displaystyle \mathbf {z} =\mathbf {H\odot r} =\math {pmatrix} 1&1&1&0&1&1&1&1&1&0\end {pmatrix1\0\1\0\1\1\0\1\1\1\1\dot {pmatrix}}$

이 연산의 결과 z(증후군)는 3 × 1 0 벡터이므로, 결과 코드워드 r이 성공적으로 검증된다.

복호화가 완료된 후, 부호어의 첫 번째 3비트를 보고, 원래의 메시지 비트 「101」을 추출할 수 있다.

설명 중에 이 삭제 예에서는 소프트 결정 디코딩 또는 소프트 결정 메시지 패싱은 사용되지 않습니다.이는 거의 모든 상용 LDPC 디코더에서 사용됩니다.

노드 정보 업데이트 중

최근에는 가변 노드 및 제약 노드 업데이트를 위한 대체 일정의 영향을 연구하는 데 많은 노력이 투입되었다.LDPC 코드를 디코딩하기 위해 사용된 원래 기술은 플래딩으로 알려져 있습니다.이러한 유형의 업데이트에서는 변수 노드를 업데이트하기 전에 모든 제약 조건 노드를 업데이트해야 하며, 그 반대도 마찬가지입니다.Vila Casado ^[21]등의 후속 연구에서는 변수 노드가 사용 가능한 최신 체크 노드 정보로 업데이트되는 대체 업데이트 기법이 연구되었다.

이러한 알고리즘의 배후에 있는 직관적인 이유는 값이 가장 많이 변화하는 가변 노드가 가장 먼저 업데이트되어야 한다는 것입니다.로그우도비(LLR)의 크기가 크고 업데이트 간에 큰 변화가 없는 고신뢰 노드에서는 기호와 크기가 더 크게 변동하는 다른 노드와 같은 빈도로 업데이트가 필요하지 않습니다.이러한 스케줄링 알고리즘은 플래딩을 사용하는 알고리즘보다 컨버전스 속도가 빠르고 에러 플로어가 낮음을 나타냅니다.이러한 에러 하한은, Informed Dynamic Scheduling(IDS;^[21] 정보 다이나믹 스케줄링) 알고리즘이 근접 코드 ^[22]워드의 트랩 세트를 극복하는 기능에 의해서 실현됩니다.

비플래딩 스케줄링 알고리즘이 사용되는 경우 반복에 대한 대체 정의가 사용됩니다.레이트 k/n의 (n, k) LDPC 코드의 경우, n 변수 및 n - k 제약조건 노드가 갱신되었을 때, 갱신 순서에 관계없이 완전한 반복이 발생합니다.

코드 구축

블록 사이즈가 큰 경우 LDPC 코드는 일반적으로 디코더의 동작을 먼저 연구하여 구축됩니다.블록 사이즈가 무한대인 경향이 있기 때문에 LDPC 디코더는 디코딩이 확실하게 달성되고 디코딩이 ^[23]달성되지 않는 노이즈 임계값을 가지고 있음을 나타낼 수 있으며, 이를 클라이프 효과라고 한다.이 임계값은 체크노드의 호 및 변수 노드의 호에서 최적의 비율을 찾아 최적화할 수 있습니다.이 임계값을 시각화하기 위한 대략적인 그래픽 접근법은 EX입니다.IT 차트

이 최적화 후의 특정 LDPC 코드 구축은 주로 다음 두 가지 유형의 기술로 분류됩니다.

• 의사 난수법
• 조합적 접근법

의사 랜덤 어프로치에 의한 구축은, 블록 사이즈가 큰 경우, 랜덤 구축이 양호한 디코딩 ^[10]성능을 제공하는 이론적 결과에 근거해 구축된다.일반적으로 의사 난수 코드에는 복잡한 인코더가 있지만, 최적의 디코더를 가진 의사 난수 코드에는 단순한 ^[24]인코더가 있을 수 있습니다.무한 블록 크기의 이론적인 한계에서 예상되는 원하는 특성이 유한 블록 크기로 발생하도록 보장하기 위해 다양한 제약 조건이 종종 적용됩니다.

콤비네이션 어프로치를 사용하면, 작은 블록 사이즈의 LDPC 코드의 속성을 최적화하거나, 심플한 인코더를 사용해 코드를 작성할 수 있습니다.

일부 LDPC 코드는 10 기가비트이더넷 ^[25]표준에서 사용되는 RS-LDPC 코드 등 Reed-Solomon 코드를 기반으로 합니다.랜덤하게 생성된 LDPC 코드와 비교하여 구조화된LDPC 코드(DVB-S2 규격에서 사용되는LDPC 코드 등)는 특히 H 매트릭스가 순환 ^[26]매트릭스가 되도록 구성된 보다 단순하고 저렴한 하드웨어로 만들 수 있습니다.

LDPC 코드를 구성하는 또 다른 방법은 유한 지오메트리를 사용하는 것입니다.이 방법은 Y에 의해 제안되었다.Kou ^[27]et al. 2001년

LDPC 코드와 터보 코드

LDPC 코드는 터보 ^[28]코드와 같은 다른 강력한 코딩 방식과 비교할 수 있습니다.한편, 터보 코드의 BER 성능은 낮은 코드 ^[29]제한에 의해 영향을 받습니다.LDPC 코드에는 최소 ^[30]거리 제한이 없습니다.이는 간접적으로 LDPC 코드가 터보 코드보다 비교적 큰 코드레이트(예를 들어 3/4, 5/6, 7/8)에서 더 효율적일 수 있음을 의미합니다.단, LDPC 코드가 완전히 대체되는 것은 아닙니다.터보 코드는 코드 레이트가 낮은 최적의 솔루션입니다(예: 1/6, 1/3, 1/2).^[31][32]

「 」를 참조해 주세요.

사람

• 로버트 갤러거
• 리처드 해밍
• 클로드 섀넌
• 데이비드 J. C.맥케이
• 어빙 S.리드
• 마이클 루비

이론.

• 믿음의 전파
• 그래프 이론
• 해밍 코드
• 선형 코드
• 스파스 그래프 코드
• 익스팬더 코드

적용들

• G.hn/G.9960 (전원선, 전화선 및 동축 케이블을 통한 네트워크용 ITU-T 표준)
• 802.3an 또는 10GBASE-T(10기가비트/초 이더넷, 트위스트 페어)
• CMMB(중국 멀티미디어 모바일 방송)
• DVB-S2 / DVB-T2 / DVB-C2 (디지털 비디오 방송, 제2세대)
• DMB-T/H(디지털 비디오 방송)^[33]
• WiMAX(마이크로파 통신용 IEEE 802.16e 규격)
• IEEE 802.11n-2009(Wi-Fi 표준)
• DOCSIS 3.1
• ATSC 3.0(차세대 북미 디지털 지상파 방송)
• 3GPP(5G-NR 데이터 채널)

기타 용량 접근 코드

• 터보 코드
• 직렬 연결 컨볼루션 코드
• 온라인 코드
• 분수 코드
• LT코드
• 랩터 코드
• 반복 누적 코드(단순 터보 코드 클래스)
• 토네이도 코드(소거 복호화를 위해 설계된 LDPC 코드)
• 폴라 코드

레퍼런스

외부 링크

• 저밀도 패리티 체크 코드 소개 (Sarah J Johnson, 2010)
• LDPC 코드– 간단한 튜토리얼 (Bernhard Leiner, 2005)
• LDPC 코드(TU Wien)
• 온라인 교과서: David J.C.의 정보 이론, 추론 및 학습 알고리즘. MacKay에서는 47장에서 LDPC 코드에 대해 설명합니다.
• 저밀도 패리티 체크 코드의 반복 디코딩 (Venkatesan Guruswami, 2006)
• LDPC 코드: 개요 (Amin Shokrollahi, 2003)
• LDPC 코드의 신뢰-전파 복호화(프린스턴 대학 Amir Bennatan)
• 터보 및 LDPC 코드: 구현, 시뮬레이션 및 표준화(West Virginia University)
• 정보 이론과 코딩(Marko Hennhöfer, 2011, TU Ilmenau) - 74-78페이지에서 LDPC 코드를 논의한다.
• LDPC 코드 및 퍼포먼스 결과
• DVB-S.2 링크(LDPC 코딩 포함)(MatLab)
• LDPC 코드의 부호화, 디코딩 및 시뮬레이션을 위한 소스 코드는, 다음의 다양한 장소에서 입수할 수 있습니다.
  • C의 바이너리 LDPC 코드
  • Python의 바이너리 LDPC 코드(C의 코어 알고리즘)
  • MATLAB의 LDPC 인코더 및 LDPC 디코더
  • 고속 LDPC 시뮬레이션을 위한 C++11의 Fast Forward Error Correction Toolbox(AFF3CT)