클라도그램

Cladogram
왼쪽에 근이 있는 수평 클래도그램
두 개의 수직 클래도그램, 하단의 근

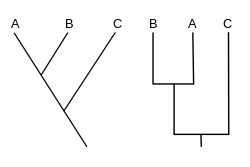
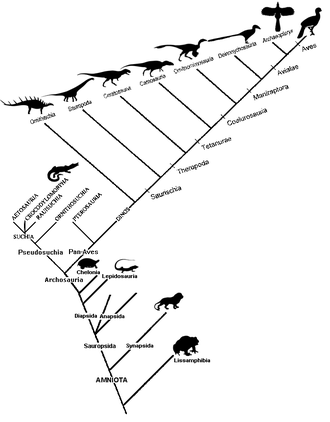
클라도그램(Cladogram)은 생물들 간의 관계를 보여주기 위해 분류학에서 사용되는 도표입니다. 그러나 클라도그램은 조상들이 후손들과 어떻게 연관되어 있는지를 보여주지도 않고, 얼마나 많이 변했는지를 보여주지도 않기 때문에 많은 다른 진화적 나무들이 같은 클라도그램과 일치할 수 있기 때문에 진화적 나무는 아닙니다.[1][2][3][4][5] 클라도그램은 마지막 공통 조상을 가진 유기체 그룹인 클레이드에서 끝나는 다른 방향으로 분기되는 선을 사용합니다. 여러 가지 모양의 클라도그램이 있지만 모두 다른 선과 분기되는 선이 있습니다. 그 선들은 그들이 분기하는 곳까지 거슬러 올라갈 수 있습니다. 이러한 분기점은 가상의 조상(실제 개체가 아님)을 나타내며, 이는 그 위의 말단 분류군 간에 공유된 특성을 나타내는 것으로 추론할 수 있습니다.[4][6] 그러면 이 가상의 조상은 조상에 대한 다양한 특징, 적응 및 기타 진화적 서술의 순서에 대한 단서를 제공할 수 있습니다. 전통적으로 이러한 클라도그램은 주로 형태학적 특성을 기반으로 생성되었지만 DNA 및 RNA 염기서열 분석 데이터와 전산 계통 발생학은 현재 클라도그램 생성에 매우 일반적으로 사용됩니다.

클래도그램 생성

새의 클라도그램

분자 대 형태학적 데이터

클래도그램을 작성하는 데 사용되는 특징은 크게 형태학적(시냅시드 두개골, 온혈, 노토코드, 단세포 등) 또는 분자학적(DNA, RNA 또는 기타 유전 정보)으로 분류할 수 있습니다.[7] DNA 염기서열 분석이 등장하기 전에는 주로 형태학적 데이터를 사용했습니다. (동물에 대한) 행동 데이터도 사용될 수 있습니다.[8]

DNA 염기서열 분석이 저렴해지고 쉬워짐에 따라, 분자 체계학은 계통발생학적 가설을 추론하는 점점 더 대중적인 방법이 되었습니다.[9] 간결성 기준을 사용하는 것은 분자 데이터에서 계통 발생을 추론하는 여러 가지 방법 중 하나일 뿐입니다. 시퀀스 진화의 명시적 모델을 통합하는 최대 가능성과 같은 접근법은 시퀀스 데이터를 평가하는 비헤니지안 방법입니다. 계통발생을 재구성하는 또 다른 강력한 방법은 유전체 레트로트랜스포존 표지자를 사용하는 것인데, 이는 서열 데이터를 괴롭히는 복귀 문제의 가능성이 낮은 것으로 생각됩니다. 그들은 또한 한때 게놈에 완전히 무작위로 통합되었다고 생각되었기 때문에 일반적으로 동형질의 발생률이 낮은 것으로 추정됩니다. 그러나 적어도 때때로는 그렇지 않은 것 같습니다.

클래디컬리즘의 한 형태. 이 도표는 조상 상태로 "A"와 "C"를 나타내고, 말기 분류군에 존재하는 상태로 "B", "D" 및 "E"를 나타냅니다. 실제로 조상의 상태는 선험적으로 알려져 있지 않지만(이 휴리스틱 예제에서 볼 수 있듯이) 터미널에서 관찰되는 공유 상태의 패턴에서 추론해야 합니다. 이 예에서 각 단자가 고유한 상태를 가지고 있다는 점을 고려할 때, 실제로 우리는 조상 상태에 대해 결정적인 어떤 것도 추론할 수 없을 것입니다(관측되지 않은 상태 "A"와 "C"의 존재가 단순하지 않은 추론일 것이라는 사실 이외에는!).

플레시오모피와 시나포피

연구자들은 어떤 문자 상태가 "조상"이고 어떤 문자 상태가 파생된 상태인지(동형)를 결정해야 합니다. 왜냐하면 시냅스 문자 상태만이 그룹화의 증거를 제공하기 때문입니다.[10] 이 결정은 일반적으로 하나 이상의 아웃그룹의 문자 상태와 비교하여 수행됩니다. 아웃그룹과 인그룹의 일부 구성원 간에 공유되는 상태는 단순 동형이며, 인그룹의 하위 집합에만 존재하는 상태는 시냅스입니다. 단일 터미널에 고유한 문자 상태(자동 형태)는 그룹화의 증거를 제공하지 않습니다. 다른 아웃그룹은 매우 다른 위상을 가진 나무를 생산할 수 있기 때문에 아웃그룹을 선택하는 것은 클래디컬 분석에서 중요한 단계입니다.

호모플라시즈

호모플라시는 공통 조상 이외의 다른 원인으로 인해 둘 이상의 분류군이 공유하는 문자 상태입니다.[11] 동형질의 두 가지 주요 유형은 수렴(적어도 두 개의 서로 다른 계통에서 "동일한" 문자의 진화)과 복귀(조상 문자 상태로의 복귀)입니다. 북극 포유류의 다른 계통에 있는 흰색 털과 같이 분명히 동종인 캐릭터는 관계에 대한 우리의 이해에 아무런 기여도 하지 않기 때문에 계통 발생 분석에 캐릭터로 포함시켜서는 안 됩니다. 그러나, 동형질은 (예를 들어, DNA 서열과 같이) 문자 자체의 검사에서 분명하지 않은 경우가 많으며, 그 다음 가장 단순한 분류도에서 그것의 불일치(비단순 분포)에 의해 검출됩니다. 동형인 문자는 여전히 계통 발생 신호를 포함할 수 있습니다.[12]

수렴 진화로 인한 동형질의 잘 알려진 예로는 "날개의 존재"라는 캐릭터가 있을 것입니다. 새, 박쥐, 곤충의 날개는 같은 역할을 하지만, 그들의 해부학적 구조에서 볼 수 있듯이 각각 독립적으로 진화했습니다. 새, 박쥐, 날개 달린 곤충이 "날개의 존재"라는 캐릭터에 점수를 매기면, 데이터 세트에 동형이 도입될 것이고, 이것은 분석을 혼란스럽게 할 수 있으며, 아마도 잘못된 관계 가설을 초래할 수 있습니다. 물론 처음에 동형이 인식될 수 있는 유일한 이유는 동형 분포를 드러내는 관계의 패턴을 암시하는 다른 문자가 있기 때문입니다.

클래도그램이 아닌 것

클래도그램은 분석 결과를 도식화한 것으로, 시냅스만을 기준으로 분류합니다. 데이터를 다소 다르게 취급하는 다른 많은 계통발생학적 알고리즘이 있고, 클라도그램처럼 보이지만 클라도그램이 아닌 계통발생학적 트리를 생성합니다. 예를 들어, UPGMA 및 Neighbor-Joining과 같은 표현형 알고리즘은 전체 유사성에 따라 그룹화하고, 시냅스와 단순형 모두를 그룹화의 증거로 취급합니다. 결과 다이어그램은 클라도그램이 아닌 페노그램입니다. 유사하게, 분기 순서와 "분기 길이"를 모두 고려한 모델 기반 방법(최대 가능성 또는 베이지안 접근법)의 결과는 시냅스와 자가형성을 모두 그룹화 또는 그룹화 반대의 증거로 계산합니다. 이러한 종류의 분석에서 얻은 다이어그램도 클래도그램이 아닙니다.[13]

Cladogram 선택

"최상의" 클래도그램을 식별하는 데 사용할 수 있는 몇 가지 알고리즘이 있습니다.[14] 대부분의 알고리즘은 데이터와 후보 클래도그램이 얼마나 일치하는지 측정하기 위해 메트릭을 사용합니다. 대부분의 클라도그램 알고리즘은 최적화와 최소화라는 수학적 기법을 사용합니다.

일반적으로 클라도그램 생성 알고리즘은 컴퓨터 프로그램으로 구현되어야 하지만, 일부 알고리즘은 데이터 세트가 완만할 때 수동으로 수행될 수 있습니다(예를 들어, 몇 종의 특성과 몇 가지).

일부 알고리즘은 특성 데이터가 분자(DNA, RNA)인 경우에만 유용하고, 다른 알고리즘은 특성 데이터가 형태적인 경우에만 유용합니다. 특성 데이터가 분자 및 형태학적 데이터를 모두 포함하는 경우 다른 알고리즘을 사용할 수 있습니다.

클라도그램 또는 다른 유형의 계통수에 대한 알고리즘은 최소 제곱, 이웃 결합, 간결성, 최대 가능성 및 베이지안 추론을 포함합니다.

생물학자들은 때때로 특정 종류의 클라도그램 생성 알고리즘에 대해 간결성이라는 용어를 사용하고, 때로는 모든 계통 발생 알고리즘에 대해 포괄적인 용어로 사용합니다.[15]

최적화 작업(예: 클래도그램 구축)을 수행하는 알고리즘은 입력 데이터(종 목록 및 특성)가 제시되는 순서에 민감할 수 있습니다. 데이터를 다양한 순서로 입력하면 동일한 알고리즘이 다른 "최상" 클래도그램을 생성할 수 있습니다. 이러한 상황에서 사용자는 다양한 순서로 데이터를 입력하고 결과를 비교해야 합니다.

하나의 데이터 세트에 다른 알고리즘을 사용하면 때때로 다른 "최상" 클래도그램을 생성할 수 있습니다. 왜냐하면 각 알고리즘은 "최상"에 대한 고유한 정의를 가질 수 있기 때문입니다.

가능한 클라도그램이 천문학적으로 많기 때문에 알고리즘은 솔루션이 전체적으로 최선의 솔루션이라고 보장할 수 없습니다. 프로그램이 원하는 전역 최소값이 아닌 로컬 최소값에 안착하는 경우 최적이 아닌 클래도그램이 선택됩니다.[16] 이 문제를 해결하는 데 도움이 되기 위해 많은 클래도그램 알고리즘은 시뮬레이션된 어닐링 접근법을 사용하여 선택된 클래도그램이 최적의 클래도그램일 가능성을 높입니다.[17]

기본 위치는 뿌리가 있는 계통수 또는 클라도그램의 기본(또는 뿌리) 방향입니다. 기저 분기군은 (주어진 분류학적 등급의) 더 큰 분기군 내에서 분기되는 가장 이른 분기군입니다.

통계학

불일치 길이 차이 검정(또는 분할 동질성 검정)

불일치 길이 차이 테스트(ILD)는 서로 다른 데이터 세트(예: 형태학적 및 분자적, 색소체 및 핵 유전자)의 조합이 더 긴 트리에 어떻게 기여하는지 측정하는 것입니다. 각 파티션의 총 트리 길이를 먼저 계산하여 합산하여 측정합니다. 그런 다음 원래 파티션으로 구성된 무작위로 조립된 파티션을 만들어 복제를 만듭니다. 길이가 합산됩니다. 99개의 반복실험이 결합된 트리 길이가 더 긴 경우 100개의 반복실험에 대해 p 값 0.01이 얻어집니다.

호몰로지 측정

자세한 정보: 수렴진화

일부 측정값은 트리를 참조하여 데이터 세트의 동형성의 양을 측정하려고 시도하지만,[18] 이러한 측정값이 정량화하는[19] 목적이 무엇인지 정확하게 명확하지는 않습니다.

일관성지수

일관성 지수(CI)는 트리가 내포하는 최소 동형사상의 양을 측정하는 데이터 집합에 대한 트리의 일관성을 측정합니다.[20] 데이터 세트의 최소 변경 횟수를 세어 클라도그램에 필요한 실제 변경 횟수로 나누어 계산합니다.[20] c로i 표시된 개별 특성에 대해 일관성 지수를 계산할 수도 있습니다.

메트릭은 동형의 양을 반영하는 것 외에도 데이터 세트의 분류군 수,[21] 데이터 세트의 문자 수,[22] 각 문자가 계통 발생 정보를 전달하는 정도, [23]추가 문자가 코딩되는 방식을 반영하여 목적에 적합하지 않습니다.[24]

c는i 짝수 상태 분포를 가진 이진 문자에서 1에서 1/[n.taxa/2]의 범위를 차지합니다. c의 최소값은 상태가 균등하게 퍼지지 않을 때 더 큽니다.[23][18] 일반적으로 n인 이진 또는 비이진 문자의 경우 c는 1에서 - /( - ⌈ n. / .⌉) {\n. /n.states⌉)}의 범위를 차지합니다.

보유지수

보존 지수(RI)는 "특정 응용 분야에 대한" CI의 개선으로 제안되었습니다.[25] 이 메트릭은 또한 동형질의 양을 측정하는 것을 목적으로 하지만 시냅스가 나무를 얼마나 잘 설명하는지도 측정합니다. (트리의 최대 변경 수에서 트리의 변경 수를 뺀 값)를 취하고 (트리의 최대 변경 수에서 데이터 세트의 최소 변경 수를 뺀 값)로 나누어 계산합니다.

리스케일 일관성 지수(RC)는 CI에 RI를 곱하여 얻어지는데, 이는 이론적으로 달성 가능한 최소값이 0으로 리스케일되도록 CI의 범위를 확장하며, 최대값은 1로 유지됩니다.[18][25] 동형 지수(HI)는 간단히 1 - CI입니다.

호모플라시 과잉 비율

이것은 이론적으로 존재할 수 있는 최대 동형질 양 – 1 - (관측된 동형질 과잉) / (최대 동형질 과잉)을 기준으로 나무에서 관찰된 동형질의 양을 측정합니다.[22] 값이 1이면 동형 사상이 없음을 나타내며, 0은 완전 무작위 데이터 세트에서 있을 수 있는 만큼의 동형 사상을 나타내고, 음수 값은 여전히 더 많은 동형 사상을 나타냅니다(그리고 작위적인 예제에서만 발생하는 경향이 있음).[22] HER은 현재 이용 가능한 동형성의 가장 좋은 척도로 제시됩니다.[18][26]

참고 항목

참고문헌

  1. ^ Mayr, Ernst (2009). "Cladistic analysis or cladistic classification?". Journal of Zoological Systematics and Evolutionary Research. 12: 94–128. doi:10.1111/j.1439-0469.1974.tb00160.x.
  2. ^ Foote, Mike (Spring 1996). "On the Probability of Ancestors in the Fossil Record". Paleobiology. 22 (2): 141–51. doi:10.1017/S0094837300016146. JSTOR 2401114. S2CID 89032582.
  3. ^ Dayrat, Benoît (Summer 2005). "Ancestor-Descendant Relationships and the Reconstruction of the Tree of Life". Paleobiology. 31 (3): 347–53. doi:10.1666/0094-8373(2005)031[0347:aratro]2.0.co;2. JSTOR 4096939. S2CID 54988538.
  4. ^ a b Posada, David; Crandall, Keith A. (2001). "Intraspecific gene genealogies: Trees grafting into networks". Trends in Ecology & Evolution. 16 (1): 37–45. doi:10.1016/S0169-5347(00)02026-7. PMID 11146143.
  5. ^ Podani, János (2013). "Tree thinking, time and topology: Comments on the interpretation of tree diagrams in evolutionary/phylogenetic systematics" (PDF). Cladistics. 29 (3): 315–327. doi:10.1111/j.1096-0031.2012.00423.x. PMID 34818822. S2CID 53357985. Archived (PDF) from the original on 2017-09-21.
  6. ^ Schuh, Randall T. (2000). Biological Systematics: Principles and Applications. ISBN 978-0-8014-3675-8.[페이지 필요]
  7. ^ DeSalle, Rob (2002). Techniques in Molecular Systematics and Evolution. Birkhauser. ISBN 978-3-7643-6257-7.[페이지 필요]
  8. ^ Wenzel, John W. (1992). "Behavioral homology and phylogeny". Annu. Rev. Ecol. Syst. 23: 361–381. doi:10.1146/annurev.es.23.110192.002045.
  9. ^ Hillis, David (1996). Molecular Systematics. Sinaur. ISBN 978-0-87893-282-5.[페이지 필요]
  10. ^ Hennig, Willi (1966). Phylogenetic Systematics. University of Illinois Press.
  11. ^ West-Eberhard, Mary Jane (2003). Developmental Plasticity and Evolution. Oxford Univ. Press. pp. 353–376. ISBN 978-0-19-512235-0.
  12. ^ Kalersjo, Mari; Albert, Victor A.; Farris, James S. (1999). "Homoplasy Increases Phylogenetic Structure". Cladistics. 15: 91–93. doi:10.1111/j.1096-0031.1999.tb00400.x. S2CID 85905559.
  13. ^ Brower, Andrew V.Z. (2016). "What is a cladogram and what is not?". Cladistics. 32 (5): 573–576. doi:10.1111/cla.12144. PMID 34740305. S2CID 85725091.
  14. ^ Kitching, Ian (1998). Cladistics: The Theory and Practice of Parsimony Analysis. Oxford University Press. ISBN 978-0-19-850138-1.[페이지 필요]
  15. ^ Stewart, Caro-Beth (1993). "The powers and pitfalls of parsimony". Nature. 361 (6413): 603–7. Bibcode:1993Natur.361..603S. doi:10.1038/361603a0. PMID 8437621. S2CID 4350103.
  16. ^ Foley, Peter (1993). Cladistics: A Practical Course in Systematics. Oxford Univ. Press. p. 66. ISBN 978-0-19-857766-9.
  17. ^ Nixon, Kevin C. (1999). "The Parsimony Ratchet, a New Method for Rapid Parsimony Analysis". Cladistics. 15 (4): 407–414. doi:10.1111/j.1096-0031.1999.tb00277.x. PMID 34902938. S2CID 85720264.
  18. ^ a b c d 에서 검토한
  19. ^ Chang, Joseph T.; Kim, Junhyong (1996). "The Measurement of Homoplasy: A Stochastic View". Homoplasy. pp. 189–203. doi:10.1016/b978-012618030-5/50009-5. ISBN 9780126180305.
  20. ^ a b Kluge, A. G.; Farris, J. S. (1969). "Quantitative Phyletics and the Evolution of Anurans". Systematic Zoology. 18 (1): 1–32. doi:10.2307/2412407. JSTOR 2412407.
  21. ^ Archie, J. W.; Felsenstein, J. (1993). "The Number of Evolutionary Steps on Random and Minimum Length Trees for Random Evolutionary Data". Theoretical Population Biology. 43: 52–79. doi:10.1006/tpbi.1993.1003.
  22. ^ a b c Archie, J. W. (1989). "Homoplasy Excess Ratios: New Indices for Measuring Levels of Homoplasy in Phylogenetic Systematics and a Critique of the Consistency Index". Systematic Zoology. 38 (3): 253–269. doi:10.2307/2992286. JSTOR 2992286.
  23. ^ a b c Hoyal Cuthill, Jennifer F.; Braddy, Simon J.; Donoghue, Philip C. J. (2010). "A formula for maximum possible steps in multistate characters: Isolating matrix parameter effects on measures of evolutionary convergence". Cladistics. 26 (1): 98–102. doi:10.1111/j.1096-0031.2009.00270.x. PMID 34875753. S2CID 53320612.
  24. ^ Sanderson, M. J.; Donoghue, M. J. (1989). "Patterns of variations in levels of homoplasy". Evolution. 43 (8): 1781–1795. doi:10.2307/2409392. JSTOR 2409392. PMID 28564338.
  25. ^ a b Farris, J. S. (1989). "The retention index and the rescaled consistency index". Cladistics. 5 (4): 417–419. doi:10.1111/j.1096-0031.1989.tb00573.x. PMID 34933481. S2CID 84287895.
  26. ^ Hoyal Cuthill, Jennifer (2015). "The size of the character state space affects the occurrence and detection of homoplasy: Modelling the probability of incompatibility for unordered phylogenetic characters". Journal of Theoretical Biology. 366: 24–32. Bibcode:2015JThBi.366...24H. doi:10.1016/j.jtbi.2014.10.033. PMID 25451518.

외부 링크

  • Wikimedia Commons의 Cladogram 관련 미디어