네이버 가입

생물정보학에서 인접접합은 1987년 ^[1]나루야 사이토우 마사토시·네이씨가 개발한 계통수 생성용 상향(응집형) 군집법이다.보통 DNA 또는 단백질 배열 데이터에 기반한 나무에 사용되는 이 알고리즘은 ^[2]트리를 형성하기 위해 각 분류군 쌍(예: 종 또는 배열) 사이의 거리에 대한 지식이 필요하다.

알고리즘

네이버 결합은 각 분류군 쌍 간의 거리를 지정하는 거리 행렬을 입력으로 받아들입니다.이 알고리즘은 스타 네트워크의 토폴로지에 대응하는 완전히 해결되지 않은 트리에서 시작하여 트리가 완전히 해결되어 모든 브랜치 길이를 알 수 있을 때까지 다음 단계를 반복합니다.

1. 현재 거리 행렬을 기반으로 $행렬{\displaystyle }$ Q$($$아래$ 정의)를 계산합니다.
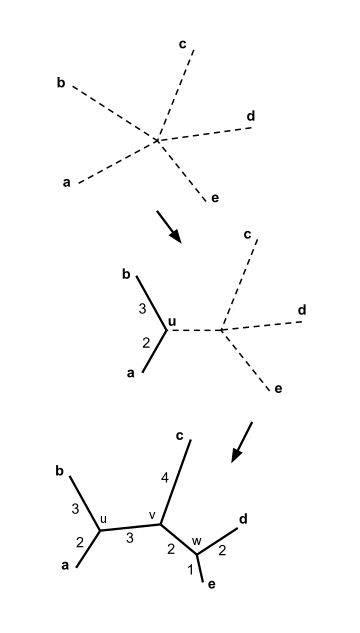
2. Q$($의 값이 가장 낮은 고유 분류법 i와 j($i$$,$$j)$의 쌍을 찾습니다.이러한 분류는 중앙 노드에 연결된 새로 생성된 노드에 결합됩니다.오른쪽 그림에서는 f와 g가 새로운 노드 u에 결합되어 있다.
3. 쌍의 각 분류군으로부터 이 새로운 노드까지의 거리를 계산합니다.
4. 이 쌍의 바깥쪽에 있는 각 분류군으로부터 새로운 노드까지의 거리를 계산합니다.
5. 알고리즘을 재기동하여 가입된 네이버 쌍을 새 노드로 교체하고 이전 단계에서 계산된 거리를 사용합니다.

Q 매트릭스

$n{\displaystyle }$\$style n$ \display $style$ Q$$$$\$displaystyle$ Q \displaystyle Q$$\를$$ 다음과 같이 $계산$합니다.

${{displaystyle Q(i,j)=(n-2)d(i,j)-\sum _{k=1}^{n}d(i,k)-\sum _{k=1}^{n}d(j,k)}$

(1)

${\displaystyle \mathrm{여기}}$서${\displaystyle }$d (${\displaystyle i}$, j$$) { $displaystyle d$ ( $i$, j ) a$$ 、$taxa{\displaystyle }$i $j$ j$$\ $displaystyle$ j$$까지의 거리입니다.

페어 멤버에서 새 노드까지의 거리

결합되는 쌍의 각 분류군에 대해 다음 공식을 사용하여 새 노드까지의 거리를 계산합니다.

$\displaystyle \displaystyle \flac {1}{2}}d(f,u)+{\frac {1}{2(n-2)}}\left[\sum _{k=1}^{n}d(f,k)-\sum _{k=1}^{n}d(g,k)\right]$

(2)

또, 다음과 같이 합니다.

$\displaystyle \display(g,u)=d(f,g)-\display(f,u)\displays }$

$Taxa{\displaystyle }$f {\$displaystyle$ f$}$와 g {\$displaystyle$ g$}$는 쌍으로 구성된 $분류군$이고$$u {\$displaystyle$u}는$$ 새로 생성된 노드입니다.f$(\displaystyle$ f$)$와$$u(\$displaystyle$u$)$와 g$(\displaystyle$ g$)$와$$u(\$displaystyle$\delta $(f,u)$와$$$displaystyle \delta (g,u))$를 $연결$하는 $브랜치들$은 점차 생성되는 트리의 일부입니다${\displaystyle .}$그 후의 네이버 설정 순서의 영향을 받습니다.

새 노드로부터의 다른 분류군 거리

이전 단계에서 고려되지 않은 각 분류군에 대해 새 노드까지의 거리를 다음과 같이 계산합니다.

${\displaystyle d(u,k)=param frac {1}{2}}[d(f,k)+d(g,k)-d(f,g)]$

(3)

$여기$서$u\displaystyle$u는$$ 새로운 노드, $\displaystyle$k는$$ 우리가 계산할 노드, $\displaystyle$f와$$ $\displaystyle$g는 방금$$ 결합된 쌍의 멤버입니다.

복잡성

네이버가 $n개($style$$ n$)$ 택시에 ${\displaystyle \mathrm{가입}}$하려면 $n{\displaystyle }$ ${\displaystyle -}$3개($display$ $style$ $n-3)$각 단계에서 Q$(디스플레이 스타일$ Q$)$ $매트릭스$를 구축하고 검색해야 합니다.처음에 $(\displaystyle$ Q$)$ 매트릭스의$$ $크기$는${\displaystyle }$n ×$$(\$displaystyle$ n$\times$ n$)$입니다.다음 단계는${\displaystyle }$(${\displaystyle n-}$ ${\displaystyle 1}$) ×${\displaystyle }$( ${\displaystyle n}$ -${\displaystyle 1}$)$$\ $displaystyle$( $n-1$) \$times$ ( $n-1$ )$。$이것을 간단하게 실장하면${\displaystyle ,}$ O$n$ 3$)({displaystyle$ O$(n^{3$^[3]의 시간 복잡도를 가지는 알고리즘이 생깁니다.실장에서는,^[4] 휴리스틱스를 사용해 평균보다 훨씬 뛰어난 성능을 발휘합니다.

예

5개의 분류군$, b, c, d, e)$과 다음의 $거리행렬{\displaystyle }$ D$(displaystyle$$$D$)$가 있다고 가정합니다.

	a	b	c	d	e
a	0	5	9	9	8
b	5	0	10	10	9
c	9	10	0	8	7
d	9	10	8	0	3
e	8	9	7	3	0

제1단계

첫 가입

$({$ 값은$$ 식 (1)에 의해 계산됩니다.예를 들어 다음과 같습니다.

${\displaystyle Q_{1}(a,b)=(n-2)d(a,b)-\sum _{k=1}^{5}d(a,k)-\sum _{k=1}^5}d(b,k)}$

${\displaystyle =(5-2)\times 5-(5+9+9+8)-(5+10+10+9)=15-31-34=-50}$

${\displaystyle {Q\mathrm{}}_{}}$ 1$(\$ $매트릭스$에 대해 다음 값을 구합니다(매트릭스의 대각 요소는 사용되지 않으며 여기서는 생략됩니다).

	a	b	c	d	e
a		−50	−38	−34	−34
b	−50		−38	−34	−34
c	−38	−38		−40	−40
d	−34	−34	−40		−48
e	−34	−34	−40	−48

위의 예에서는 ${\displaystyle {Q\mathrm{}}_{}}$1 (${\displaystyle a,b}$ )$=$ - ${\displaystyle 50}${ $displaystyle Q_{1}(a,$b)=-$50$ 입니다.이 ${\displaystyle {값}_{}}$은$Q1$의 최소값({$displaystyle$$Q_$${$1$\})$이므로 요소$$$a$와$b$를 결합합니다.

첫 번째 분기 길이 추정

u$\displaystyle$는 새로운$$ 노드를 나타냅니다.위의 식 (2)에 따르면,$a$와$$$b$를 연결하는 branch의 $길이는$$다음$과 같습니다$.$

$\displaystyle \displaystyle \flac {1}{2}d(a,u)+{\frac {1}{2-2)}}\left[\sum _{k=1}{5}d(a,k)-\sum _{k=1}{5}d(b,k)\right]\sum ={frac5}{frac}{fr}{frc}{fr}$

$\displaystyle \display (b,u)=d(a,b)-\display (a,u)\displays = 5-2=3}$

첫 번째 거리 매트릭스 업데이트

그런 다음 초기 거리 $D$를 새로운 $거리{\displaystyle {}_{}}$ 매트릭스 $($아래 참조)로 업데이트합니다. 이 행렬은$$b$\$$displaystyle$b를$$ $가진{\displaystyle }$ $\displaystyle$ a$}$가 $이웃$하는$$u\$displaystyle$u에 결합되었기 때문에 크기가 1줄 1줄 축소됩니다.위 (3)에서는$u$(\$displaystyle$u)에서 a(\$displaystyle$ a$)$및$$ $(\displaystyle$ b$)$ $이외$의 각 노드까지의 거리를 계산합니다.이 경우 다음과 같이 구합니다.

${\displaystyle d(u,c)=paramfrac {1}{2}}[d(a,c)+d(b,c)-d(a,b)]=paramfrac {9+10-5}{2}}=7}$

${\displaystyle d(u,d)=paramfrac {1}{2}}[d(a,d)+d(b,d)-d(a,b)]=paramfrac {9+10-5}{2}}=7}$

${\displaystyle d(u,e)=paramfrac {1}{2}}[d(a,e)+d(b,e)-d(a,b)]=paramfrac {8+9-5}{2}}=6}$

결과 거리 $행렬{\displaystyle {}_{}}$ $(\$은 다음과 같습니다.

	u	c	d	e
u	0	7	7	6
c	7	0	8	7
d	7	8	0	3
e	6	7	3	0

$(\$의 굵은 글씨 값은 새로 계산된 거리에 해당하지만 이탤릭체로 표시된 값은 첫 번째 분류에 포함되지 않은 요소 간의 거리에 해당하므로 매트릭스 업데이트의 영향을 받지 않습니다.

두 번째 단계

두 번째 가입

$대응$하는 $({$ 매트릭스는$$ 다음과 같습니다.

	u	c	d	e
u		−28	−24	−24
c	−28		−24	−24
d	−24	−24		−28
e	−24	−24	−28

$사용자{\displaystyle }$ 및 c$\$$displaystyle$c$$또는$$$$d$\displaystyle$ d$\$$displaystyle$ e$\backslash$$displaystyle$ e $중{\displaystyle }$ 하나를 선택할 수 있습니다$.$$두$ 쌍의 ${\displaystyle {Q2\mathrm{}}_{}}$(\$displaystyle Q_{$2}) 값은 최소$$(\$displaystyle -28$입니다. 어느 쪽을 선택해도 같은 결과가 됩니다.구체적으로는$u와$${displaystyle$ c$}$에 $참여$하여 새로운 $노드{\displaystyle }$ v${displaystyle$ v$\}$를 호출합니다.

두 번째 분기 길이 추정

사용자$(\displaystyle$u)와 c$(\displaystyle$ c$)$에서 v$(\displaystyle$ v$)$까지의 분기 길이를 계산할 수 있습니다.

$\displaystyle \displaystyle \displayfrac {1}{2}d(u,v)+{\frac {1}{2-2)}\left[\sum _{k=1}{4}d(u,k)-\sum _{k=1}{4}d(c,k)\right]\displayfrac {{frac}{frac7}$

$\displaystyle \display (c,v)=d(u,c)-\display (u,v)\displays = 7-3=4}$

요소의 결합과 분기 길이 계산은 그림에 나타나듯이 인접 결합 트리를 그리는 데 도움이 됩니다.

두 번째 거리 매트릭스 업데이트

이제 나머지 3개 노드$($$v{\displaystyle }$\$displaystyle$ v$),$$$d$\displaystyle$ d 및$e{\displaystyle }$$\$displaystyle e$)$에 대해 업데이트된 거리 행렬 D2$({$ $D_{2$})가 계산됩니다.

${\displaystyle d(v,d)=param frac {1}{2}}[d(u,d)+d(c,d)-d(u,c)]=param frac {7+8-7}{2}}=4}$

${\displaystyle d(v,e)=param frac {1}{2}}[d(u,e)+d(c,e)-d(u,c)]=param frac {6+7-7}{2}}=3}$

	v	d	e
v	0	4	3
d	4	0	3
e	3	3	0

마지막 단계

이 시점에서 트리 토폴로지는 완전히 해결됩니다.단, 알기 쉽게 하기 위해 $매트릭스$를 계산할 수 있습니다({$3})$ $매트릭스$를 계산할 수 있습니다.예를 들어 다음과 같습니다.

${\displaystyle Q_{3}(v,e)=(3-2)d(v,e)-\sum _{k=1}^{3}d(e,k)=3-7-6=-10}$

	v	d	e
v		−10	−10
d	−10		−10
e	−10	−10

구체적으로는 v${displaystyle$ v$}$와$$d{$displaystyle$ d$}$에 접속하여 마지막 $노드$를 w$\displaystyle$ w$\}$합니다.나머지 3개의 분기의 길이를 계산할 수 있습니다.

$(\displaystyle \displaystyle (v,w)=paramfrac {1}{2-3)}}\left[\sum _ {k=1}{3}d(d,k)\right]\param={frac4}{frc}{2}}\left}$

$\displaystyle \display (w,d)=d(v,d)-\display (v,w)=4-2=2}$

$\displaystyle \display(w,e)=d(v,e)-\display(v,w)=3-2=1}$

그림에서 보듯이 네이버 가입 트리가 완료되었습니다.

결론: 가법 거리

이 예는 이상적인 경우를 나타내고 있습니다.트리의 가지를 따라 임의의 분류군에서 다른 분류군으로 이동하여 횡단한 분기의 길이를 합하면 결과는 입력 거리 매트릭스 내의 분류군 간의 거리와 동일합니다.예를 들어 d$\displaystyle$d에서$$ $\displaystyle$b로$$ $넘어가면{\displaystyle \mathrm{}}$ 2${\displaystyle }$+${\displaystyle 2}$ +${\displaystyle }$3 + ${\displaystyle 3}$ $=$ ${\displaystyle 10}$ \ $displaystyle$ 2 $+ 2$ +$3$ + 3 $=$ 10 \ displaystyle 2 + 3 = $10$ \ displaystyle 2 + 3 + 3 $=$ 10 \ displaystyle displaystyle tree for for for whose whose whose for whose for for for whose for whose for 、 、 ' whose whose whose whose ' whose whose whose그럼에도 불구하고, 추가 거리 행렬이 입력으로 주어졌을 때, 분류군 사이의 거리가 일치하는 트리를 찾을 수 있는 인접 결합이 보장된다는 것을 유념하는 것이 중요하다.

최소 진화로서의 네이버 가입

네이버 가입은 Balanced Minimum^[5] Evolution(BME) 기준에 대한 탐욕적인 휴리스틱으로 간주될 수 있습니다.BME는 각 토폴로지에 대해 트리 길이(분기 길이의 합계)를 토폴로지에 따라 가중치를 갖는 거리 매트릭스 내의 특정 가중치 합계로 정의합니다.BME 최적 토폴로지는 이 트리 길이를 최소화하는 토폴로지입니다.각 단계에서 이웃이 결합하면 추정된 나무 길이가 가장 크게 감소하는 한 쌍의 분류군에 탐욕스럽게 결합됩니다.이 순서에서는, BME 기준에 최적인 것을 찾는 것을 보증하는 것은 아닙니다.다만, BME 기준에 최적인 것을 알 수 있는 경우가 많아, 통상은 매우 가깝습니다.

장점과 단점

NJ의 주요 장점은 최소 제곱, 최대 절약 및 최대 우도 ^[6]방법에 비해 빠르다는^{[6]: 466} 것이다.이를 통해 대규모 데이터 세트(수백 또는 수천 개의 분류군)를 분석하고 부트스트래핑(bootstraping)을 수행할 때 실용적이므로 다른 분석 수단(예: 최대 절약성, 최대 가능성)이 계산상 불가능할 수 있습니다.

네이버 가입에는 입력 거리 매트릭스가 올바르면 출력 트리가 올바르다는 속성이 있습니다.게다가 거리행렬이 「거의 가법」인 한,^[7] 특히 거리행렬의 각 엔트리가 트리내의 최단 분기길이의 절반 미만으로 실제 거리로부터 다른 경우, 출력 트리 토폴로지의 정확성이 보증된다.실제로는 거리행렬이 이 조건을 만족시키는 경우는 거의 없지만 네이버 가입에 의해 ^[8]올바른 트리토폴로지가 구축되는 경우가 많습니다.거의 가법 거리 행렬에 대한 인접 결합의 정확성은 많은 진화 모델에서 통계적으로 일관성이 있음을 의미한다. 충분한 길이의 데이터가 주어지면 인접 결합은 높은 확률로 진정한 트리를 재구성할 것이다.UPGMA 및 WPGMA와 비교하여 네이버 가입은 모든 계통이 같은 속도로 진화하는 것을 전제로 하지 않는다는 장점이 있습니다(분자 클럭 가설).

그럼에도 불구하고, 인접 결합은 거리 측정에 의존하지 않고 대부분의 ^{[citation needed]}조건에서 우수한 정확도를 제공하는 계통 발생학적 방법으로 대체되었다.네이버 가입에는 바람직하지 않은 기능이 있어 대부분의 경우 브랜치 중 일부에 마이너스 길이를 할당합니다.

구현 및 변형

네이버 가입을 구현하는 프로그램은 많이 있습니다.RapidNJ와 NINJA는 빠른 구현으로, 일반적인 실행 시간은 분류군의 약 제곱에 비례합니다.BIONJ와 Weeighbor는 일반적으로 장거리보다 짧은 거리가 더 잘 알려져 있다는 사실을 이용하여 정확성을 향상시키는 네이버 결합의 변형입니다.FastME는 밀접하게 관련된 최소 균형 진화 방법을 구현한 것입니다.

「 」를 참조해 주세요.

• 가장 가까운 네이버 검색
• UPGMA 및 WPGMA
• 최소 진화

레퍼런스

기타 소스

외부 링크

• Neighbor-Joining 메서드: 튜토리얼