벤트의 법칙

Bent's rule
실제 결합각 104.5°가 이상적인3 sp각 109.5°에서 벗어난 것을 보여주는 물 분자의 형상.

화학에서 Bent의 법칙은 궤도 혼성화와 치환기의 전기음성도 사이의 관계를 설명하고 설명합니다.[1][2] 이 규칙은 Henry A에 의해 명시되었습니다. 다음과 같이 구부러집니다.[2]

원자의 특성은 전기 양성 치환기를 향한 궤도에 집중됩니다.

원자가 결합 이론은 분자 구조에 대한 좋은 근사치를 제공합니다. 벤트의 법칙은 관측된 기하학과 이상화된 기하학 사이의 차이를 해결합니다.[3] 벤트의 법칙에 따르면 여러 그룹에 결합된 중심 원자는 다시 혼성화되어 더 많은 특성을 가진 오비탈은 전기 양성 그룹으로 향하고, 더 많은 p 특성을 가진 오비탈은 더 전기 음성 그룹으로 향합니다. 모든 하이브리드 오비탈이 동등하다는 가정을 제거함으로써, Bent의 규칙은 분자 기하학과 결합 강도의 향상된 예측으로 이어집니다.[4][5] 벤트의 법칙은 s와 궤도의 상대적인 에너지 수준을 통해 정당화될 수 있습니다. 벤트의 법칙은 이상적인 대칭보다 낮은 분자에 대한 VSEPR 이론의 수정을 나타냅니다.[6] 낮은 시기의 더 큰 원자와의 결합의 경우, 궤도 혼성화의 경향은 전기 음성도와 궤도 크기 모두에 크게 의존합니다.

역사

1930년대 초, 양자역학의 초기 개발의 많은 부분이 있은 직후, [7]폴링, [8]슬레이터, [9]콜슨 등에 의해 분자 구조에 적용되기 시작했습니다. 특히 폴링은 원자와 p궤도가 결합하여 혼성 sp, sp2, sp궤도를3 주는 혼성화 개념을 도입했습니다. 혼성 궤도는 네 개의 등가 C-H 결합 사이에 sp3 탄소 원자와 109.5°의 결합 각도를 가진 사면체인 메탄과 같은 단순 분자의 분자 기하학을 설명하는 데 강력한 것으로 증명되었습니다. 그러나, 이러한 이상적인 기하학으로부터 약간의 편차가 1940년대에 명백해졌습니다.[10] 특히 잘 알려진 예로는 물이 있는데, 두 O-H 결합 사이의 각도는 104.5°에 불과합니다. 그러한 불일치를 설명하기 위해, 혼성화는 비등식 및 p 특성을 갖는 궤도를 초래할 수 있다고 제안되었습니다. 1947년 A. D. Walsh는[10] 탄소에 결합된 그룹의 전기음성도와 탄소 원자의 혼성화 사이의 관계를 설명했습니다. 마침내 1961년에 Bent는 분자 구조, 중심 원자 혼성화 및 치환기 전기음성도와 관련된 문헌에 대한 주요 리뷰를 발표했으며 이 작업을 위해 Bent의 규칙이 그 이름을 따게 되었습니다.

Bent의 원래 논문은 메틸 치환이 포름산과 아세트산의 산 해리 상수를 감소시키기 때문에 메틸기의 그룹 전기음성도가 수소 원자의 그룹 전기음성도보다 낮은 것으로 간주합니다.[2]

비결합궤도

Bent의 법칙은 비결합 궤도의 혼성화를 합리화하기 위해서도 확장될 수 있습니다. 한편으로, 전자 밀도가 중심 원자를 향해 완전히 편광된, 단독 쌍(점유된 비결합 궤도)은 전기양성 치환기의 제한적인 경우로 생각될 수 있습니다. Bent의 법칙은 공유되지 않은 밀접하게 붙잡힌 비결합 전자를 안정화하기 위해서는 단독 쌍 궤도가 높은 특성을 가져야 한다고 예측합니다. 반면에, 전자 밀도가 리간드 쪽으로 완전히 편광되고 중심 원자에서 멀어지는, 비어 있는(빈) 비결합 오비탈은 전기 음성 치환기의 제한적인 경우로 생각될 수 있습니다. Bent의 법칙은 남은 점유 궤도에 가능한 많은 특성을 남기기 위해서는 점유되지 않은 비결합 궤도가 p 특성을 최대화해야 한다고 예측합니다.

실험적으로 첫 번째 결론은 메탄에 비해 물이나 암모니아 같은 단독 쌍을 가진 분자의 결합 각도가 줄어든 것과 일치하고, 두 번째 결론은 단량체 보란이나 카르베늄 이온과 같이 비어 있는 비결합 오비탈을 가진 분자의 평면 구조와 일치합니다.

결과들

Bent의 법칙은 분자 구조와 반응성의 경향을 설명하는 데 사용될 수 있습니다. 중심 원자의 혼성화가 특정 특성에 어떤 영향을 미치는지 결정한 후, 치환기의 전기음성도를 조사하여 Bent의 규칙이 유지되는지 확인할 수 있습니다.

결합각: VSEPR 이론과 Bent's Rule

원자가 결합 이론은 메탄이 사면체이고 에틸렌이 평면이라고 예측합니다. 물과 암모니아에서는 결합각이 각각 104.5°와 107°로 예상 사면체각 109.5°보다 작기 때문에 상황이 더 복잡합니다. 이러한 편차에 대한 한 가지 근거는 VSEPR 이론으로, 여기서 원자가 전자는 국부적인 영역에 위치하고 단독 쌍은 결합 쌍보다 서로 더 많이 밀어내는 것으로 가정됩니다. 벤트의 법칙은 대안적인 설명을 제공합니다.

Skeletal structures and bond angles of arbitrary alkanes, alkenes, and alkynes.
임의의 알칸, 알켄 및 알킨의 골격 구조 및 결합 각도.

원자가 쉘 전자쌍 반발(VSEPR) 이론은 분자 기하학을 예측합니다.[11][12] VSEPR은 분자기하학이 전자쌍을 가장 많이 띄울 수 있는 배열을 취할 것으로 예측합니다.[11][12] 이 전자 거리 최대화는 가장 안정적인 전자 분포를 달성하기 위해 발생합니다.[11][12] VSEPR 이론의 결과는 결합 각도를 정확하게 예측할 수 있다는 것입니다. VSEPR 이론에 따르면 분자의 기하학적 구조는 중심 원자에 연결된 전자쌍과 원자의 수를 세어 예측할 수 있습니다.[11][12] 벤트의 법칙은 "A]토믹의 특성은 전기 양성 치환기를 향한 궤도에 집중된다"[2]고 말합니다. 벤트의 법칙은 결합각이 VSEPR 이론에 의해 예측된 결합각에서 벗어날 것이라는 것을 암시하고, 중심 원자를 둘러싼 원자들의 상대적인 전기음성도는 분자 기하학에 영향을 미칠 것입니다.[5] VSEPR 이론은 간단한 규칙을 이용하여 분자 형태를 정확하게 예측하는 방법을 제시합니다.[13] 그러나 VSEPR 이론은 관측된 분자 결합 각도를 대략적으로만 예측합니다.[13][14] 반면에 벤트의 법칙이 더 정확합니다.[5] 또한 분자기하학을 설명할 때 Bent의 법칙이 양자역학적 계산을 확증한다는 것이 밝혀졌습니다.[15]

분자 치환기 사이의 결합 각도 Bond Angle을 사용한 3D 영상
디메틸에테르 		111.5° ± 1.5°[16]
메탄올 		108.5° ± 2°[17]
물. 		104.5°[18]
디플루오르화 산소 		104.2°[19]

위의 표는 VSEPR 이론이 예측한 결합 각도와 실제 각도의 차이를 보여줍니다. VSEPR 이론에 따르면 디에틸에테르, 메탄올, 물, 이산화산소는 모두 109.5의o 결합각을 가져야 합니다.[12] VSEPR 이론을 이용하면, 이 모든 분자들은 같은 "굽은" 모양을 가지고 있기 때문에 같은 결합 각도를 가져야 합니다.[12] 그러나 분명히 이 모든 분자들 사이의 결합 각도는 다른 방식으로 이상적인 기하학적 구조에서 벗어납니다. 벤트의 법칙은 이러한 명백한 불일치를 설명하는 데 도움이 될 수 있습니다.[5][20][21] 전기 음성 치환기는 더 많은 p 특성을 가질 것입니다.[5][20] 결합 각도는 s 문자와 비례 관계를 가지며 p 문자와 역의 관계를 갖습니다.[5] 따라서 치환기가 더 전기적으로 음성이 될수록 분자의 결합 각도는 감소해야 합니다. 디메틸에테르, 메탄올, 물 및 디플루오르화 산소는 예상대로 이 추세를 따릅니다(위 표에 표시됨). 두 개의 메틸기는 디에틸에테르의 중심 산소에 붙어 있는 치환기입니다. 두 메틸기는 전기 양성이기 때문에 더 큰 특성이 관찰되고 실제 결합 각도는 이상적인 결합 각도인 109.5보다o 더 큽니다. 메탄올은 1개의 전기양성 메틸 치환기와 1개의 전기음성 수소 치환기를 가지고 있습니다. 따라서 디메틸에테르보다 특성이 덜 관찰됩니다. 수소 치환기가 2개일 경우 전기음성도와 p의 특성이 증가함에 따라 각도가 더욱 감소하게 됩니다. 마지막으로 두 수소 치환기를 모두 디플루오르화 산소에서 불소로 치환하면 결합 각도가 또 감소합니다. 불소는 전기적으로 매우 부정적이기 때문에 결합 각도가 크게 감소합니다.

물의 결합 각도를 예측할 때 Bent의 규칙은 더 많은 s 특성을 가진 하이브리드 오비탈이 단독 쌍을 향해야 하는 반면, 더 많은 p 특성을 가진 오비탈이 수소를 향하게 하여 25%의 s 특성과 75%의 p 특성을 가진 이상화된 O(sp3) 하이브리드 오비탈에서 벗어난다는 것을 시사합니다. 물의 경우 104.5° HOH 각도로 OH 결합 오비탈은 O4.0(~sp) 오비탈(~20%s, ~80%p)로 구성되는 반면, 단독 쌍은 O(~sp2.3) 오비탈(~30%s, ~70%p)로 구성됩니다. 위의 정당화에서 논의한 바와 같이, 단독 쌍은 매우 전기적인 양의 치환기로서 행동하고 과잉의 특성을 갖습니다. 그 결과 결합 전자가 p자성을 높였습니다. 이러한 오비탈의 증가된 p 문자는 그들 사이의 결합 각도를 사면체 109.5° 미만으로 감소시킵니다. 동일한 논리를 암모니아(107.0° HNH 결합 각도, 3개의 N(~sp3.4 또는 23% s) 결합 오비탈과 1개의 N(~sp2.1 또는 32% s) 단독 쌍)에도 적용할 수 있습니다.

질소 함유 화합물도 같은 추세입니다. VSEPR 이론의 예상과는 달리, Bent의 법칙과 일치하며 암모니아(NH3)와 삼불화질소(NF3)의 결합 각도는 각각 107°와 102°입니다.

이제 이론적 토대가 흔들리는 것처럼 보이는 VSEPR 이론과는 달리, 벤트의 법칙은 현대의 결합 치료에서 여전히 중요한 원리로 여겨집니다.[5][22] 예를 들어, HO의 단독 쌍이 대칭성으로 인해 동일하지 않다고 간주되더라도(즉, s만, 평면 내 p 및 p 산소 AO가 혼성화되어 두 O-H 결합 궤도 σ 및 단독 쌍 n을 형성하는 반면 p는 동일하지 않은 순수 p-문자 단독 쌍 n이 됨), 이 분석을 수정하는 것은 여전히 가능합니다. 자연적인 결합 궤도 방법에서 나온 고독한 쌍의 경우와 마찬가지로.

중심 원자에 결합된 두 종류의 원자를 갖는 디플루오로메탄과 같은 사면체 분자의 경우, 더 많은 전기 음성 치환기(F)에 대한 C-F 결합은 C-H 결합보다 더 적은 특성을 갖는 탄소 오비탈을 포함하므로, C-F 결합 사이의 각도는 109.5°[15][23]의 사면체 결합 각도보다 작습니다.

삼각형 바이피라미드 분자는 축과 적도 위치를 모두 가지고 있습니다. 두 종류의 치환기가 있는 경우, 두 개의 적도 치환기 사이의 결합 각도보다 축과 전기 음성 치환기 사이의 결합 각도가 작으므로 전기 음성 치환기가 축 위치를 더 선호할 것입니다.[23]

본드길이

결합 각도와 마찬가지로 원자의 혼성화는 원자가 형성하는 결합의 길이와 관련이 있을 수 있습니다.[2] 결합 궤도가 특성이 증가할수록 σ 결합 길이는 감소합니다.

분자 평균 탄소-탄소 결합 길이
Two sp3 carbon atoms bonded to each other. 1.54Å
One sp3 and one sp2 carbon bonded to each other. 1.50Å
One sp3 and one sp carbon bonded to each other. 1.46Å

전기 음성 치환기를 추가하고 중심 원자의 혼성화를 변경하여 결합 길이를 조작할 수 있습니다. 분자가 구조 X-A-Y를 포함하는 경우, 치환기 X를 더 전기적인 음의 원자로 대체하면 중심 원자 A의 혼성화가 변경되고 인접한 A-Y 결합이 짧아집니다.

분자 평균 탄소-불소 결합 길이
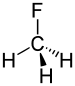Skeletal structure of fluoromethane.
플루오로메탄		 1.388Å
Skeletal structure of difluoromethane.
디플루오로메탄		 1.358Å
Skeletal structure of trifluoromethane.
트리플루오로메탄		 1.329Å
Skeletal structure of tetrafluoromethane.
테트라플루오로메탄		 1.323Å

서로 다른 전기 음성도를 가진 원소들 사이의 결합은 극성을 띠고 이러한 결합의 전자 밀도는 더 많은 전기 음성 소자 쪽으로 이동할 것입니다. 이 개념을 플루오로메탄이라는 분자에 적용하면 벤트 법칙의 힘을 알 수 있습니다. 탄소가 수소보다 전기적으로 더 음이기 때문에 C-H 결합의 전자 밀도는 짧아지고 C-F 결합은 길어질 것입니다.

염소가 불소보다 전기적으로 덜 부정적이기 때문에 효과가 덜 극적이지만, 메탄의 염소화된 유사체도 같은 추세를 유지합니다.[2]

분자 평균 탄소-염소 결합 길이
Skeletal structure of chloromethane.
클로로메탄		 1.783Å
Skeletal structure of dichloromethane.
디클로로메탄		 1.772Å
Skeletal structure of trichloromethane.
트리클로로메탄		 1.767 Å
Skeletal structure of tetrachloromethane.
테트라클로로메탄		 1.766Å

위의 사례들은 염소의 크기가 전기음성도보다 덜 중요하다는 것을 보여주는 것 같습니다. 입체 물질만을 기반으로 한 예측은 반대의 경향으로 이어질 것입니다. 큰 염소 치환기는 멀리 떨어져 있는 것이 더 유리하기 때문입니다. 입체적인 설명이 실험 결과와 모순되기 때문에, Bent의 법칙이 구조 결정에 주요한 역할을 할 것으로 보입니다.

JCH 커플링 상수

아마도 수소와 탄소 사이의 결합 궤도에서 s의 특성을 가장 직접적으로 측정하는 것은 NMR 스펙트럼에서 결정된13 H-C 결합 상수를 통한 것일 것입니다. 이론은CH J 값이 s 문자와 상관관계가 있다고 예측합니다.[24] 특히. 하나의 결합 C-H 결합 상수 J는 경험적 관계 J C- H = χ(i)displaystyle \ ^{1}J_{^{mathrm {C} -^{1}\mathrm {H} = (500\ \mathrm {Hz})\chi_{\mathrm {s}(i)}, 여기서χi) s}}(i)}는 s 문자입니다. (예를 들어 메탄의 C-H 결합에서 발견되는 순수한 sp 하이브리드 원자 궤도는 25%의 문자를 가지며, 실험적으로 결정된 값과 매우 일치하는 500Hz × 0.25 = 125Hz의 예상 결합 상수를 갖게 됩니다.)

분자 JCH(메틸 양성자 중)
Skeletal structure of methane.
메탄		 125Hz
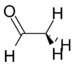Skeletal structure of acetaldehyde.
아세트알데히드		 127Hz
Skeletal structure of 1,1,1-trichloroethane.
1,1,1–Trichloroethane		 134Hz
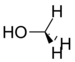Skeletal structure of methanol.
메탄올		 141Hz
Skeletal structure of fluoromethane.
플루오로메탄		 149Hz

치환기의 전기음성도가 증가함에 따라 치환기를 향하는 p 문자의 양도 증가합니다. 이것은 메틸 양성자에 대한 결합에 더 많은 특성을 남겨 J 결합CH 상수를 증가시킵니다.

귀납효과

귀납적 효과는 Bent의 법칙으로 설명할 수 있습니다.[25] 유도 효과는 공유 결합을 통한 전하의 전달이며, Bent의 법칙은 혼성화의 차이를 통해 그러한 결과에 대한 메커니즘을 제공합니다. 아래 [26]표에서 중심 탄소에 결합된 그룹이 더 전기적으로 음수가 될수록 중심 탄소는 극성 치환기 상수로 측정하면 더 많은 전자 인출이 됩니다. 극치 치환 상수는 증가하는 값이 더 큰 전자 인출 능력에 해당하므로 원칙적으로 Hammett 방정식의 σ 값과 유사합니다. Bent의 법칙은 그룹의 전기 음성도가 증가함에 따라 더 많은 p개의 문자가 해당 그룹으로 전환되어 중심 탄소와 R 그룹 사이의 결합에 더 많은 문자가 남는다는 것을 시사합니다. 오비탈이 p 오비탈보다 핵에 가까운 전자 밀도를 가지므로 C-R 결합의 전자 밀도는 특성이 증가할수록 탄소 쪽으로 더 많이 이동합니다. 이렇게 하면 중심 탄소가 R기로 전자를 더 많이 인출할 수 있습니다.[10] 따라서, 유도 효과가 예측하는 바와 같이, 치환기의 전자 인출 능력은 인접한 탄소로 전달되었습니다.

치환기 극성 치환기 상수
(larger 값은 더 큼을 의미합니다.
전자 withdraw링 능력)
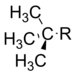An arbitrary t-Butyl group.
t–부틸		 −0.30
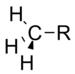An arbitrary methyl group.
메틸		 0.00
A chloromethyl group bonded to R.
클로로메틸		 1.05
A dichloromethyl group bonded to R.
디클로로메틸		 1.94
A trichloromethyl group bonded to R.
트리클로로메틸		 2.65

형식론

벤트의 법칙은 원자가 결합 이론에 추가적인 수준의 정확도를 제공합니다. 원자가 결합 이론은 공유 결합이 두 개의 결합 원자로부터 중첩된, 보통 혼성화된 원자 궤도에 놓여 있는 두 개의 전자로 구성된다고 제안합니다. 공유 결합이 단지 두 결합 원자의 원자 궤도의 선형 결합이라는 가정은 근사치입니다(분자 궤도 이론 참조). 그러나 원자가 결합 이론은 결합을 이해하는 방법에 큰 영향을 미쳤고 계속해서 영향을 미칠 정도로 정확합니다.[1]

원자가 결합 이론에서 두 개의 원자는 각각 원자 궤도를 기여하고 궤도 중첩에 있는 전자는 공유 결합을 형성합니다. 원자는 보통 순수한 수소와 같은 오비탈을 결합에 기여하지 않습니다.[7] 만약 원자가 수소와 같은 궤도에만 기여할 수 있다면, 실험적으로 확인된 메탄의 사면체 구조는 탄소의 2s와 2p 궤도가 그러한 기하학적 구조를 가지고 있지 않기 때문에 가능하지 않을 것입니다. 그와 다른 모순들이 궤도 교배의 제안으로 이어졌습니다. 그 틀에서 원자 궤도는 서로 다른 모양과 에너지를 가진 동일한 수의 궤도를 생성하기 위해 혼합될 수 있습니다. 앞서 언급한 메탄의 경우, 탄소의 2s와 3개의 2p 오비탈이 혼성화되어 4개의 동등한3 스비탈이 생성되며, 이는 구조 불일치를 해결합니다. 궤도 교잡은 원자가 결합 이론이 방대한 수의 분자의 기하학과 특성을 성공적으로 설명할 수 있게 해주었습니다.

전통적인 혼성화 이론에서, 혼성 궤도들은 모두 동등합니다.[12][27] 즉 원자와 p 오비탈을 결합하여 4개의 sp=1 ⁄√4(s + √3p) 오비탈, 3개의 sp=1 √3(s + ⁄√2p) 오비탈 또는 2개의 sp=1 ⁄√2(s + p) 오비탈을 제공합니다. 이들 조합은 두 가지 조건을 만족시키기 위해 선택됩니다. 첫째, s와 p 궤도 기여의 총량은 혼성화 전후에 동등해야 합니다. 둘째, 하이브리드 궤도는 서로 직교해야 합니다.[27][28] 두 개의 하이브리드 오비탈이 직교하지 않으면 정의에 따라 0이 아닌 오비탈 중첩이 발생합니다. 이러한 오비탈에 있는 전자들은 상호작용을 할 것이고, 만약 그 오비탈들 중 하나가 공유 결합에 관여한다면, 다른 오비탈들 또한 그 결합과 0이 아닌 상호작용을 할 것이고, 이것은 원자가 결합 이론의 결합 원리당 두 개의 전자를 위반하는 것입니다.

하이브리드와 p 오비탈을 구성하려면 첫 번째 하이브리드 오비탈을 s + √λp로 지정하고 여기서 p는 결합 그룹을 향하고 λ는 이 하이브리드 오비탈이 갖는 p 캐릭터의 양을 결정합니다. 이것은 파동 함수의 가중합입니다. 이제 두 번째 혼성 오비탈 + √λp를 선택합니다. 여기서 p는 어떤 식으로든 방향을 잡고 λ은 두 번째 오비탈의 p 문자의 양입니다. 결과 오비탈이 정규화될 수 있고 첫 번째 하이브리드 오비탈과 직교할 수 있도록 λ와 p의 방향의 값이 결정되어야 합니다. 하이브리드는 두 개의 정규화된 파동 함수의 합이므로 확실히 정규화될 수 있습니다. 두 개의 혼성 오비탈이 별개의 공유 결합에 관여할 수 있도록 직교성이 확립되어야 합니다. 직교 오비탈의 내적은 0이어야 하며, 구성된 하이브리드의 내적을 계산하면 다음과 같은 계산이 가능합니다.

s 오비탈은 정규화되므로 내부 곱 ⟨ s ⟩ = 1이 됩니다. 또한 s 오비탈은 p와 p 오비탈과 직교하므로 위의 동일한 0에서 두 항으로 이어집니다. 마지막 항은 정의에 따라 코스 ω을 부여하는 서로 ω의 각도에 있는 두 정규화 함수의 내적입니다. 그러나 결합 궤도의 직교성은 1 + √λλ cos ω = 0을 요구하므로 결과적으로 다음과 같은 쿨슨 정리를 얻을 수 있습니다.

이는 모든 계수 λ이 위의 조건을 쌍으로 만족시켜 결과 오비탈이 직교한다는 것을 보장한다면 4개의 원자 오비탈과 p개의 원자 오비탈이 임의의 방향으로 혼성화될 수 있음을 의미합니다.

중심 원자가 더 큰 p 특성의 오비탈을 더 많은 전기 음성 치환기로 향하게 한다는 벤트의 법칙은 λ 계수의 증가가 s + √λp 하이브리드 오비탈의 p 특성을 증가시킨다는 점에 주목함으로써 위에 쉽게 적용할 수 있습니다. 따라서 중심원자 A가 X와 Y의 두 그룹에 결합되어 있고 Y가 X보다 전기적으로 더 음이라면, A는 λ < λ이 되도록 혼성화될 것입니다. 첫 번째 원리로부터 분자기하학을 정확하게 예측하기 위해서는 벤트의 법칙을 넘어서는 좀 더 정교한 이론적, 계산적 기법이 필요합니다. 하지만 벤트의 법칙은 분자 구조를 설명하는 데 탁월한 휴리스틱을 제공합니다.

헨리 벤트는 1960년에 경험적 근거로 그의 법칙을 처음 제안했지만, 몇 년 후 러셀 드라고에 의해 분자 궤도 계산에 의해 뒷받침되었습니다.[23]

Bent's rule의 적용

벤트의 법칙은 분자 기하학을 정확하게 특성화할 수 있습니다.[11][5] 벤트의 법칙은 분자의 결합 각도를 예측하는 신뢰할 수 있고 강력한 프레임워크를 제공합니다. 실제 분자의 기하학적 구조를 예측하는 벤트의 규칙 정확성과 정확성은 계속해서 그 신뢰성을 증명하고 있습니다.[5][15] 결합각 예측을 넘어, 벤트의 법칙은 몇 가지 중요한 응용 분야가 있으며 화학자들에게 상당한 관심을 가지고 있습니다.[11][5][14][21][30] Bent의 법칙은 결합 상호작용과 분자 합성을 분석하는 데 적용될 수 있습니다.

Bent의 법칙은 출발 물질에 따라 유기 합성에서 어떤 제품이 선호되는지 예측하는 데 사용할 수 있습니다.[14][30] Wang et al. 는 치환기들이 실라벤젠의 평형에 어떤 영향을 미치는지를 고찰한 결과, Bent의 법칙이 결과에 중요한 역할을 한다는 것을 발견했습니다.[14] Wang et al.이 수행한 연구는 Bent의 법칙이 합성 경로와 제품의 안정성을 예측하는 데 어떻게 사용될 수 있는지를 보여줍니다.[14] Dubois et al. 이와 유사한 응용을 보여주면서, 그들이 반응이 되돌릴 수 없다는 것을 발견했을 때, Bent의 법칙을 사용하여 그들의 발견 중 일부를 정당화할 수 있었습니다.[30] 이 두 연구는 합성 화학을 돕기 위해 어떻게 Bent의 법칙을 사용할 수 있는지를 보여줍니다. Bent의 법칙으로 인해 분자 기하학이 정확히 어떻게 되는지 알면 합성 화학자들은 상대적인 제품 안정성을 예측할 수 있습니다.[14][30] 또한 벤트의 법칙은 화학자들이 특정 제품에 대한 반응을 유도하기 위해 출발 물질을 선택하는 데 도움을 줄 수 있습니다.[14] 따라서 Bent의 법칙은 합성 화학자들이 관심 있는 반응을 더 잘 통제할 수 있게 해줍니다.

참고 항목

참고문헌

  1. ^ a b Weinhold, F.; Landis, C. L. (2005), Valency and Bonding: A Natural Donor-Acceptor Perspective (1st ed.), Cambridge: Cambridge University Press, ISBN 978-0-521-83128-4
  2. ^ a b c d e f g Bent, H. A. (1961), "An appraisal of valence-bond structures and hybridization in compounds of the first-row elements", Chem. Rev., 61 (3): 275–311, doi:10.1021/cr60211a005
  3. ^ Foster, J. P.; Weinhold, F. (1980), "Natural hybrid orbitals", J. Am. Chem. Soc., 102 (24): 7211–7218, doi:10.1021/ja00544a007
  4. ^ Alabugin, I. V.; Bresch, S.; Gomes, G. P. (2015). "Orbital Hybridization: a Key Electronic Factor in Control of Structure and Reactivity". J. Phys. Org. Chem. 28 (2): 147–162. doi:10.1002/poc.3382.
  5. ^ a b c d e f g h i j Jonas, V.; Boehme, C.; Frenking, G. (1996-01-01). "Bent's Rule and the Structure of Transition Metal Compounds". Inorganic Chemistry. 35 (7): 2097–2099. doi:10.1021/ic951397o. ISSN 0020-1669.
  6. ^ Alabugin, I. V.; Bresch, S.; Manoharan, M. (2014). "Hybridization Trends for Main Group Elements and Expanding the Bent's Rule Beyond Carbon: More than Electronegativity". J. Phys. Chem. A. 118 (20): 3663–3677. Bibcode:2014JPCA..118.3663A. doi:10.1021/jp502472u. PMID 24773162.
  7. ^ a b Pauling, L. (1931), "The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules", J. Am. Chem. Soc., 53 (4): 1367–1400, doi:10.1021/ja01355a027
  8. ^ Slater, J. C. (1931), "Directed Valence in Polyatomic Molecules", Phys. Rev., 37 (5): 481–489, Bibcode:1931PhRv...37..481S, doi:10.1103/PhysRev.37.481
  9. ^ Coulson, C. A. (1961), Valence (2nd ed.), Oxford: Clarendon Press
  10. ^ a b c Walsh, A. D. (1947), "The properties of bonds involving carbon", Discuss. Faraday Soc., 2: 18–25, doi:10.1039/DF9470200018
  11. ^ a b c d e f Ball, D. W.; Key, J. A. "Molecular Shapes and Polarity".{{cite web}}: CS1 maint: 다중 이름: 저자 목록 (링크)
  12. ^ a b c d e f g Esselman, Brian J.; Block, Stephen B. (2019-01-08). "VSEPR-Plus: Correct Molecular and Electronic Structures Can Lead to Better Student Conceptual Models". Journal of Chemical Education. 96 (1): 75–81. doi:10.1021/acs.jchemed.8b00316. ISSN 0021-9584.
  13. ^ a b Gillespie, R. J. (2008-07-01). "Fifty years of the VSEPR model". Coordination Chemistry Reviews. 252 (12): 1315–1327. doi:10.1016/j.ccr.2007.07.007. ISSN 0010-8545.
  14. ^ a b c d e f g Wang, Xuerui; Huang, Ying; An, Ke; Fan, Jinglan; Zhu, Jun (November 2014). "Theoretical study on the interconversion of silabenzenes and their monocyclic non-aromatic isomers via the [1,3]-substituent shift: Interplay of aromaticity and Bent's rule". Journal of Organometallic Chemistry. 770: 146–150. doi:10.1016/j.jorganchem.2014.08.018.
  15. ^ a b c Ghosh, Dulal C.; Bhattacharyya, Soma (January 2005). "Computation of quantum mechanical hybridization and dipole correlation of the electronic structure of the F 3 B–NH 3 supermolecule". International Journal of Quantum Chemistry. 105 (3): 270–279. doi:10.1002/qua.20690. ISSN 0020-7608.
  16. ^ Kimura, Katsumi; Kubo, Masaji (1959-01-01). "Structures of Dimethyl Ether and Methyl Alcohol". The Journal of Chemical Physics. 30 (1): 151–158. doi:10.1063/1.1729867. ISSN 0021-9606.
  17. ^ Venkateswarlu, Putcha; Gordy, Walter (1955-07-01). "Methyl Alcohol. II. Molecular Structure". The Journal of Chemical Physics. 23 (7): 1200–1202. doi:10.1063/1.1742240. ISSN 0021-9606.
  18. ^ Hankins, D.; Moskowitz, J. W.; Stillinger, F. H. (1970-12-15). "Water Molecule Interactions". The Journal of Chemical Physics. 53 (12): 4544–4554. doi:10.1063/1.1673986. ISSN 0021-9606.
  19. ^ Hilton, A. Ray; Jache, Albert W.; Beal, James B.; Henderson, William D.; Robinson, R. J. (1961-04-01). "Millimeter Wave Spectrum and Molecular Structure of Oxygen Difluoride". The Journal of Chemical Physics. 34 (4): 1137–1141. doi:10.1063/1.1731711. ISSN 0021-9606.
  20. ^ a b "1.2: VSEPR Theory and its Utility". Chemistry LibreTexts. 2019-08-15. Retrieved 2023-12-06.
  21. ^ a b Grabowski, Sławomir J. (2011-11-10). "Halogen Bond and Its Counterparts: Bent's Rule Explains the Formation of Nonbonding Interactions". The Journal of Physical Chemistry A. 115 (44): 12340–12347. doi:10.1021/jp205019s. ISSN 1089-5639.
  22. ^ Weinhold, F.; Landis, Clark R. (2012). Discovering Chemistry with Natural Bond Orbitals. Hoboken, N.J.: Wiley. pp. 67–68. ISBN 9781118119969.
  23. ^ a b c Huheey, James E. (1983). Inorganic Chemistry (3rd ed.). p. 230. ISBN 0-06-042987-9.
  24. ^ H. Friebolin (2008). Basic One- and Two- Dimensional NMR Spectroscopy (4 ed.). VCH. ISBN 978-3-527-31233-7.
  25. ^ Bent, H. A. (1960), "Distribution of atomic s character in molecules and its chemical implications", J. Chem. Educ., 37 (12): 616–624, Bibcode:1960JChEd..37..616B, doi:10.1021/ed037p616
  26. ^ Taft Jr., R. W. (1957), "Concerning the Electron—Withdrawing Power and Electronegativity of Groups", J. Chem. Phys., 26 (1): 93–96, Bibcode:1957JChPh..26...93T, doi:10.1063/1.1743270
  27. ^ a b c Coulson, C. A. (1961), Valence (2nd ed.), Oxford: Clarendon Press, pp. 203–5 Non–equivalent hybrids
  28. ^ Zhong, Ronglin; Zhang, Min; Xu, Hongliang; Su, Zhongmin (2016). "Latent harmony in dicarbon between VB and MO theories through orthogonal hybridization of 3σ g and 2σ u". Chemical Science. 7 (2): 1028–1032. doi:10.1039/C5SC03437J. ISSN 2041-6520. PMC 5954846. PMID 29896370.
  29. ^ Pfennig, Brian W. (2015). "10". Principles of Inorganic Chemistry. John Wiley and Sons. ISBN 9781118859018. Retrieved 11 August 2023. Equation (10.11) is also known as Coulson's theorem
  30. ^ a b c d Dubois, Maryne A. J.; Rojas, Juan J.; Sterling, Alistair J.; Broderick, Hannah C.; Smith, Milo A.; White, Andrew J. P.; Miller, Philip W.; Choi, Chulho; Mousseau, James J.; Duarte, Fernanda; Bull, James A. (2023-05-19). "Visible Light Photoredox-Catalyzed Decarboxylative Alkylation of 3-Aryl-Oxetanes and Azetidines via Benzylic Tertiary Radicals and Implications of Benzylic Radical Stability". The Journal of Organic Chemistry. 88 (10): 6476–6488. doi:10.1021/acs.joc.3c00083. ISSN 0022-3263. PMC 10204094. PMID 36868184.