세레이션(아카고로지)

고고학에서 톱니 모양은 같은 문화권의 수많은 유적지에서 온 조립품이나 유물들을 연대순으로 배열하는 상대적인 연대 측정 방법이다.방사성 탄소 같은 절대 연대 측정 방법을 적용할 수 없는 경우 고고학자들은 고고학적 발견과 특징의 연대를 측정하기 위해 상대 연대 측정 방법을 사용해야 한다.톱니 모양은 고고학에서 연대를 측정하는 표준 방법이다.그것은 석기, 도자기 조각, 그리고 다른 공예품들의 연대를 밝히는데 사용될 수 있다.유럽에서는 공동묘지의 무덤의 연대순을 재구성하는 데 자주 사용되어 왔다(예: Jörgensen 1992;^[1] Mussemeier, Niebeler 등 2003^[2]).

콘텍스트 및 주파수 세레이션

맥락적 연속성과 빈도 연속성의 두 가지 다른 변형이 적용되었다 (Renfrew 및 Bahn 1996, 페이지 116–117).문맥적 연속성은 설계 스타일의 유무에 기초하는 반면 주파수 연속성은 설계 스타일의 비례적 풍부성 또는 빈도를 측정하는 데 의존합니다.문맥적 톱니 모양은 설계 스타일이나 유형의 유무만 중요하기 때문에 무덤의 연대순서 재구성에 자주 사용됩니다.주파수 세레이션은 같은 스타일에 속하는 오브젝트가 많은 경우에 적용된다.예를 들어, 각각은 비율은 다르지만 거의 같은 종류의 도기 조각들을 조립하는 것이다.

역사

플린더스 페트리는 19세기 말 이집트 디오스폴리스 파르바에서 발굴했다.그는 그가 발굴한 무덤에는 그들의 연대를 알 수 있는 증거가 없고 그들의 분리된 성격은 그들의 층서학을 통해 시퀀스를 구성할 수 없음을 의미한다는 것을 발견했다.페트리는 각 무덤의 내용물을 골판지 조각에 나열하고 그가 ^[3]만족하는 순서에 도달할 때까지 서류를 교환했다.그는 가장 정확한 시퀀스는 특정 설계 스타일의 농도가 논문 시퀀스에 걸쳐 가장 짧은 지속 시간을 갖는 것이라고 추론했다(Renfrew and Bann 1996, 페이지 116; Kendall 1971, 페이지 215; Shennan 1997, 페이지 341).^[4]Petrie는 컨텍스트 연속성의 발명자로 여겨지는 반면, Brainerd(1951)^[5]와 Robinson(1951)^[6]은 주파수 연속성의 문제를 최초로 해결했다(Shennan 1997, 페이지 342).^[4]

모델

모델 설명

디자인 스타일이 인기 곡선을 따른다는 가정은 주파수 연속화의 기초를 제공합니다. 즉, 천천히 시작하여 정점으로 성장한 후 다른 스타일이 인기를 끌면서 사라집니다.또, 같은 문화권내에서, 사이트 마다 디자인의 인기는 대체로 비슷할 것이라고 상정하고 있습니다.또한 다양한 디자인 스타일의 수명이 겹치는 것이 중요합니다.이러한 규칙에 따라 특정 스타일의 비율이 가장 비슷한 사이트가 항상 함께 있도록 객체 집합을 순서대로 배치할 수 있습니다(Lock 2003, 페이지 125).

함정

설계 스타일을 식별하는 작업, 즉 동일한 설계 스타일에 속하는 객체 그룹을 형성하는 작업은 결코 간단하지 않습니다.활자를 자주 만드는 것은 연속성의 기본이다.유형 오류는 연속 오류의 원인이 됩니다.예를 들어, 특정 설계 스타일에 인기(이중 분포)가 두 개 있는 경우, 이 설계 스타일은 연속성에 적합하지 않으며 분석에 포함되면 이상한 결과가 발생할 수 있습니다.어떤 디자인 스타일은 만들어진 모양이 편리하고 개량이나 장식이 추가되지 않았기 때문에 매우 오랫동안 사용되었다.물론, 이러한 디자인 스타일은 시간순으로 정렬할 수 없습니다.예를 들어 중세 초기 유럽에서 칼은 연대순의 변화를 보이지 않는다고 한다.

시간적 구성뿐만 아니라, 톱니질 결과는 사회적 지위, 나이, 성별 또는 지역적 변화(또는 이러한 두 가지 이상의 요소의 조합)에 따른 조합 차이를 반영할 수 있다.Shennan(1997, 페이지 343)^[4]은 단검, 도끼, 검과 같은 유물 유형을 바탕으로 덴마크 호어의 톱니형 결과를 제시한다.종류 선택으로 인한 연대순이 아니라, 순서는 극단적으로 남성적인 말에서 시작하여 극단적으로 여성적인 말에서 끝나는 것 같습니다.

연대순 연속성을 위한 세 가지 조건

도란과 호드슨(1975, 페이지 269)^[7]은 연대순 연속성 결과를 얻기 위해 충족해야 하는 세 가지 조건을 열거한다.

• 지역별 변동은 최소한으로 유지해야 합니다. 즉, 어셈블리는 한 지역에서 도출하는 것이 가장 좋습니다.
• 분석 대상들은 모두 하나의 문화적 전통에서 나온 것이어야 한다.
• 톱니 모양에 포함된 특성 또는 속성은 (기능이 아닌) 문화적 측면에 따라 달라야 합니다.

통계적 방법

세레이션 방법의 개발

오늘날, 세레이션 결과는 더 이상 Petrie 시대처럼 수동으로 생성되지 않고 적절한 알고리즘에 의해 생성된다.David George Kendall(1971년)에 따르면, Petrie의 논문은 이미 톱니바퀴 문제의 수학에 대한 깊은 이해를 보여주었다(인용: "..내가 보기에 페트리는 19세기 가장 위대한 응용 수학자 중 한 명으로 꼽힐 것이다.박스터(2003, 페이지 8) 고고학 통계 랜드마크 목록에서 로빈슨(1951)의 논문은 ^[6]첫 번째 항목이다.로빈슨은 그의 주파수 세레이션법을 유사행렬에 기초했다.1971년 켄달은 톱니질 문제에 다차원 스케일링 기법의 사용을 제안했고, 이 접근방식은 일부 다른 과학자들에 의해서도 사용되었다. (백스터 2003 페이지 202–203 참조)백스터는 또한 연속성을 위한 통계적 방법의 검토와 이러한 접근법에 대한 설명을 제시한다(202–207페이지).1975년, 도란과 호드슨(269–281)^[7]은 켄달과 로빈슨의 접근법에 대한 자세한 설명을 제공하면서 톱니꼴 방법의 기술 상태를 철저히 요약했다.

연속 분석을 위한 대응 분석

오늘날 문맥적 문제와 빈도적 문제 모두에서 가장 인기 있는 세레이션 방법은 대응 분석에 기초하고 있다.대응 분석의 첫 번째 축 시퀀스는 최상의 톱니 순서로 간주된다(Shennan 1997,^[4] 페이지 342; Lock 2003, 페이지 127; Jensen & Höilund Nielsen 1997).이 기술을 사용하여 오브젝트의 순서뿐만 아니라 디자인 스타일의 순서도 확립할 수 있습니다.계산된 시퀀스의 방향을 설정하기 위해서는 외부 증거가 필요합니다. 즉, 방법은 시퀀스의 첫 번째 오브젝트가 가장 오래된 오브젝트인지 가장 어린 오브젝트인지 알 수 없습니다.

켄달(1971)은 뮌헨의 묘지 데이터에 다차원 척도를 적용했다.결과 산점도는 무덤이 시간순으로 곡선에 배열된 말굽의 형태를 보여 주었다.마찬가지로, 고려된 설계 스타일이 한 요인(연대기 등)으로만 제어되는 경우 대응 분석 결과의 처음 두 축에 대한 성분 점수 매핑은 포물선을 표시합니다.이것은 힐과 고흐(1980)^[8]에 의해 아치 효과라고 불린다.Kendall과 Jensen & Höilund Nielsen(1997년)은 포물선이 이상적인 상황에서 나타난다는 것을 보여주기 위해 인공 데이터 세트를 만들었다.따라서 대응 분석의 첫 번째 두 축의 산점도를 조사하여 다른 요인도 역할을 하는지 확인하는 것이 좋습니다(예 2 및 3 참조).

둘 이상의 요인이 중요한 경우 아치 효과로 인해 결과가 왜곡될 수 있습니다.Hill and Gauch(1980)는 이 효과를 제거하는 방법을 제시했다.

2003년에 Groenen과 Poblome은 대응 분석 알고리즘을 채택하여 seriation을 절대 날짜 ^[9][10]및 층서 관계와 결합하였다.

예

예 1: 작은 컨텍스트세레이션

아래의 작은 예는 렌프루와 반(1996년, 페이지 117년)에 의해 출판된 플린더스 페트리가 이집트 도자기를 연달아 주문하면서 영감을 얻었다.

원시 데이터는 별 기호로 컨텍스트에서 찾을 수 있는 설계 스타일을 나타내는 정렬되지 않은 이항 분할표에 저장됩니다.예를 들어 첫 번째 열을 고려합니다. 컨텍스트 3에는 블랙림, 병 및 손잡이 디자인 스타일이 포함되어 있습니다.비커는 콘텍스트1과 콘텍스트2에 포함되어 있습니다.콘텍스트 세레이션은 스타 기호가 테이블의 대각선에 가능한 한 가깝게 발견되도록 설계 스타일과 콘텍스트를 정렬합니다.물론 이와 같은 작은 예에서는 최적의 순서를 찾기 위해 컴퓨터 프로그램이 필요하지 않지만, Petrie가 연구한 900개의 무덤과 같은 대규모 데이터 세트의 경우 매우 유용합니다.

예 2: 시뮬레이션 데이터, 세레이션 및 대응 분석

이 예에서 제시된 데이터는 WinBasp에 의해 시뮬레이션되었습니다.처음에 60개의 컨텍스트(WinBasp에서는 유닛이라고 불린다)가 50개의 타입과 함께 작성되었습니다.콘텍스트는 01 ~60 의 순서로 라벨이 붙여져 타입은 T00001 ~T00050 의 형식으로 라벨이 붙여져 있습니다.유형이 하나의 개체로 표시되는 경우 이 개체만 다른 컨텍스트에 대한 링크를 제공하지 않으므로 시간순서와는 관련이 없습니다.마찬가지로 1개의 오브젝트만을 포함하는 컨텍스트는 seriation과 무관합니다.따라서 오브젝트 및 타입이1개 또는 0개 또는1개 오브젝트로 표현되지 않은 컨텍스트는 삭제되었습니다.43개의 컨텍스트와 34개의 유형으로 구성된 원시 시뮬레이션 데이터가 왼쪽에 표시됩니다.예상대로 컨텍스트 내의 타입 발생을 나타내는 점은 테이블의 대각선에 가깝다.

오른쪽 이미지는 이 데이터 세트에 대한 세레이션 결과를 보여 줍니다.원시 데이터에 비해 테이블의 대각선을 따라 점이 훨씬 더 작습니다.이것은, seriation의 경미한 문제를 나타내고 있습니다.실제로 생산 간격은 알고리즘에 의해 계산된 간격보다 다소 길 수 있습니다.일반적으로 연속 알고리즘에 의해 계산된 컨텍스트와 유형의 시퀀스는 정확한 시간순서열은 아니지만 상당히 유사합니다.

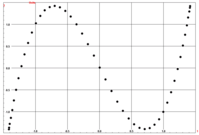
위의 이미지는 시뮬레이션된 데이터 세트의 컨텍스트에 대한 대응 분석의 처음 두 축의 전형적인 포물선 모양을 가진 산점도입니다.

예 3: 이상적인 데이터, 세레이션 및 대응 분석

분할표는 Kendall과 Jensen & Höilund Nielsen(위 참조)이 작성한 이상적인 연속성 데이터를 가진 29가지 맥락을 보여준다.새로운 컨텍스트마다 새로운 유형이 나타나고 다른 유형이 사라집니다.이 정규 데이터에서는 시간에 인접한 컨텍스트에 대해 일정한 시간 간격을 가정하는 것이 타당하다고 생각됩니다.

아래 그림에 나타난 대응 분석 결과는 이상적인 연속성 데이터를 가진 49가지 맥락을 바탕으로 계산되었다.처음 두 대응 분석 축의 산점도에는 일반적인 포물선 모양이 표시됩니다.첫 번째 및 세 번째 축에 점수가 표시되며 3도 다항식 곡선에 있는 점이 표시됩니다.마찬가지로, 첫 번째 축과 네 번째 축의 점수 그림에서는 이상적인 데이터에 대한 4차 다항식을 보여 줍니다.

첫 번째 축의 인접 컨텍스트 점수 거리는 다음과 같습니다.시작과 끝에서는 거리가 매우 작으며, 중심에서 가장 큰 거리는 가장 작은 거리의 약 30배입니다.힐과 가우치(^[8]1979)는 각 맥락이 6가지 유형을 포함하는 규칙적인 구조를 가진 유사한 분할표를 작성했다.또, 콘텍스트내의 거리는, 중간보다 끝부분이 작다는 점도 지적하고 있습니다.이것이 그들이 디렌딩 대응 분석이라고 불리는 조정을 제안한 이유 중 하나였다.

그럼에도 불구하고, 일부 고고학자들은 알려진 절대 날짜에 기초한 첫 번째 축의 점수 선형 변환이 알려지지 않은 절대 날짜에 대한 좋은 추정치를 만들어 낼 것이라고 생각하고, 이 접근법은 상대적인 날짜와 절대적인 날짜를 결합하기 위해 Groenen과 Poblome(위 참조)에 의해 제시된 방법의 기초이다.이 이상적인 예는 van de Velden, Groenen 및 Poblome의 시뮬레이션 연구에서 접근법의 예측이 상당히 ^[11]좋다는 결론에 도달했지만 선형 변환이 모든 경우에 적절하지는 않을 수 있음을 보여준다.

고고학적 순서

이 섹션은 확인을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2016년 8월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

특정 고고학적 장소에서의 고고학적 시퀀스(또는 시퀀스)는 두 가지 수준의 엄격함으로 정의될 수 있습니다.

1. 일반적으로 그것은 고고학적 기록과 동일시하기에 충분하다.그러나 이 두 용어가 정확히 서로 호환되지는 않습니다.'고고학적 기록'이라는 용어는 그 의미가 더 넓으며, 생물학적 사실과 Manuports와 같은 인공물과 다른 증거뿐만 아니라 현장의 지층학에도 적용될 수 있다.또한, 고고학적 순서와 고고학적 층서학이라는 용어는 밀접하게 관련되어 있고 어느 정도 호환성이 있다.이러한 구어적 용어의 사용은 대화에서 일반적으로 사용됩니다만, 다음과 같습니다.
2. '시퀀스'라는 용어는 좁게 정의되어 진지한 글에서 사용될 때, 계층화에 의해 밝혀진 특정 장소 또는 고고학적 기록의 분리된 부분의 층서학을 말한다.그것은 고고학적 맥락의 연속이며, 그들 사이의 관계가 그들의 층서학적 관계에 의해 연대순으로 순서를 만든다.즉, 층서학적 콘텍스트를 퇴적시키는 사건이 여러 콘텍스트의 연구로부터 결정될 수 있는 순서로 차례차례 일어났다.이것은 이 일련의 사건들이 고고학적 순서이다.

「 」를 참조해 주세요.

• 고고학 협회
• 고고학적 맥락
• 고고학적 단계
• 굴착
• 해리스 행렬
• 중첩의 법칙 – 형성되지 않은 층서열에서는 가장 오래된 층이 시퀀스의 맨 아래에 있습니다.
• 서수(통계) – 고고학에서의 연속과 같은 목적이지만 주로 생태학에서 사용된다.
• 역지층학
• 시퀀스 – 고고학적 기록의 층서학으로, 상대 연대 측정의 '연계' 방법의 일부로 사용됩니다.
• 시퀀스 연대 측정 – 도자기 양식과 시기를 연결하는 고고학적 상대 연대 측정 방법

메모들

레퍼런스

• 백스터, M. (2003)고고학의 통계학.런던:아놀드.ISBN 0-340-76299-3.
• 페이건, B. (2005)고대 북미.런던:템즈앤드허드슨
• 얀센(미국):Die frühbronzeitlichen Gréberfelder von Halawa, Shamseddin, Derniye, Tawi und Wreide am Mittleren Euphrat.Versuch einer Datierung and Deutung Sozialer Strukturen an hand multivariator 통계관 Verfahren (Korespectenzanalyse und Seriation).Ugarit Forschungen 34, Munster 2002.
• 젠슨, C.K., K.회일룬 닐슨(1997).매장 데이터 및 대응 분석.젠슨, C.K., K.에서Höilund Nielsen (에드)매장 및 사회: 고고학적 매장 데이터의 연대기 및 사회 분석.오르후스 대학 출판부, 페이지 29-61.ISBN 87-7288-686-2.
• 켄달, D.G.(1971년)"풍요행렬의 연속"고고학과 역사과학의 수학.편집 : F. R. Hodson, D. G. Kendall, P.타우투, 페이지 215~252.에든버러: 에든버러 대학 출판부.ISBN 0-85224-213-1.
• 잠금, G. (2003)고고학에서 컴퓨터를 사용하는 것: 가상 과거를 향해.런던: 루트리지.ISBN 0-415-16770-1.
• 오브라이언, 마이클 J. 그리고 R.Lee Lyman(1999년).톱니 모양, 층서학 및 색인 화석: 고고학적 연대 측정의 백본.뉴욕: 프레넘 프레스.ISBN 0-306-46152-8.
• C. 렌프루와 P. 반(1996년).고고학. 이론, 방법 및 실천.런던:템즈앤드 허드슨ISBN 0-500-276867-9.
• 시그문트, F. (2015년)대응 분석을 수행하는 방법. 고고학적 실천에 대한 짧은 안내서입니다.Charleston SC: CreateSpace. 2015.ISBN 978-1-5153-5347-8.

외부 링크

• WINBASP – Seriation 프로그램 (Windows)
• CAPCA – Excel 기반 Seriation 프로그램(Windows)
• R패키지 세레이션 (Windows/Linux/OS X)
• 과거 3.x 대응 분석, 디트렌딩 CA 또는 표준 CA를 계산하는 외빈드 해머(Oslo)의 프리 소프트웨어.
• 주파수 세레이션에 대한 단계별 소개