단위 거리 그래프
Unit distance graph수학, 특히 기하학적 그래프 이론에서 단위 거리 그래프는 두 점 사이의 거리가 정확히 1일 때마다 두 점을 모서리로 연결함으로써 유클리드 평면의 점들의 집합에서 형성된 그래프이다.이러한 그래프를 더 큰 계열의 하위 그래프와 구별하기 위해 엄밀한 단위 거리 그래프 또는 충실한 단위 거리 그래프라고 할 수 있다.유전적인 그래프 계열로서 금지된 유도 하위 그래프로 특징지을 수 있다.단위 거리 그래프에는 선인장 그래프, 성냥개비 그래프 및 페니 그래프 및 하이퍼큐브 그래프가 포함됩니다.일반화 피터슨 그래프는 단위 거리 그래프의 하위 그래프입니다.
단위 거리 그래프 n가 몇 개의 모서리를 가질 수 있는지 알 수 없습니다. 하한은 약간 초선형이며 상한(큰 O 표기로 표시됨)은 O 4/ O입니다단위 거리 그래프에 색을 입히는 데 필요한 색상 수도 알 수 없습니다. 일부 단위 거리 그래프에는 5가지 색상이 필요하며 모든 단위 거리 그래프를 7가지 색상으로 색칠할 수 있습니다.모든 대수적 숫자에 대해 두 개의 정점이 있는 단위 거리 그래프가 있습니다.모든 단위 거리 그래프를 유지하는 평면의 유일한 변환은 등각선입니다.
단위 거리 그래프를 효율적으로 작성할 수 있습니다.모든 단위 거리를 찾는 것은 패턴 매칭에 적용되며, 여기서 더 큰 패턴의 일치된 복사본을 찾는 첫 번째 단계로 사용할 수 있습니다.그러나, 주어진 그래프를 단위 거리 그래프로 나타낼 수 있는지 여부를 결정하는 것은 NP-hard이며, 보다 구체적으로 실재론의 실존 이론에 대해 완전하다.
정의.
평면의 점 집합에 대한 단위 거리 그래프는 이러한 점을 정점으로 하는 무방향 그래프이며, 유클리드 거리가 정확히 1일 때마다 두 정점 사이에 모서리가 있습니다.추상 그래프는 그 정점에 대해 평면에서 다른 위치를 찾을 수 있고, 그 가장자리가 단위 길이를 가지며, 모든 비인접 정점의 쌍이 단위 거리를 가지면 단위 거리 그래프라고 한다.이것이 가능한 경우 지정된 그래프는 선택한 위치의 단위 거리 그래프와 동형입니다.또는 일부 소스는 더 넓은 정의를 사용하여 인접하지 않은 정점 쌍을 단위 거리에 둘 수 있습니다.결과 그래프는 단위 거리 그래프의 하위 그래프입니다(여기서 [2]정의).이러한 그래프의 이름이 애매할 수 있는 경우, 비에지가 단위 거리 떨어져 있어야 하는 그래프를 엄격한 단위 거리[3] 그래프 또는 충실한 단위 거리 [2]그래프라고 할 수 있다.단위 거리 그래프의 하위 그래프는 모서리 [4]길이가 하나만 있는 평면에 그릴 수 있는 그래프입니다.
단위 거리 그래프는 단위 디스크 그래프와 혼동하지 마십시오.단위 디스크 그래프는 거리가 1 이하일 때 포인트의 쌍을 연결하고 무선 통신 [5]네트워크의 모델링에 자주 사용됩니다.
예
두 정점의 전체 그래프는 세 정점의 전체 그래프(삼각형 그래프)와 마찬가지로 단위 거리 그래프이지만 네 [3]정점의 전체 그래프는 아닙니다.삼각형 그래프를 일반화하면, 모든 주기 그래프는 단위 거리 그래프로,[4] 정다각형으로 실현됩니다.두 개의 유한 단위 거리 그래프가 하나의 공유 정점에 연결되어 있는 경우, 두 개의 그래프 중 하나를 다른 그래프에 대해 회전시켜 바람직하지 않은 추가 [6]단위 거리를 피할 수 있기 때문에 결과는 다시 단위 거리 그래프가 됩니다.이와 같이 그래프를 연결함으로써 모든 나무와 선인장 그래프를 단위 거리 [7]그래프로 실현할 수 있다.
단위 거리 그래프의 데카르트 곱은 다른 단위 거리 그래프를 생성합니다.그러나 일반적으로 사용되는 다른 그래프 제품에는 해당되지 않습니다.경로 그래프의 데카르트 곱은 모든 차원의 그리드 그래프를 형성하고, 두 꼭지점에 있는 완전한 그래프의 데카르트 곱은 하이퍼큐브 [8]그래프이며, 삼각 그래프의 데카르트 곱은 Hamming H ( ,3 ) \ H ( ,3 )[9]} 입니다.
단위 거리 그래프인 기타 특정 그래프로는 피터슨 그래프,[10] 휴우드 그래프,[11] 휠 W 거리 [3]그래프인 유일한 휠 그래프 모저 스핀들 및 골롬 그래프(4색 단위 거리 그래프)[12] 등이 있습니다.표시된 뫼비우스-칸토르 그래프와 같은 모든 일반화 페테르센 그래프는 단위 거리 [13]그래프의 하위 그래프이다.
매치스틱 그래프는 모서리가 교차하지 않는 단위 거리 그래프의 특수한 경우입니다.모든 매치스틱 그래프는 평면 [14]그래프이지만 일부 평면 단위 거리 그래프(Moser 스핀들 등)는 모든 표현에서 단위 거리 그래프로 교차합니다.또한 단위 거리 그래프에서 "평면"이라는 용어는 일부 저자가 교차 [3]금지 대신 단위 거리가 정의된 평면을 참조하기 위해 사용하기 때문에 주의해야 한다.페니 그래프는 단위 거리 그래프와 매치스틱 그래프의 훨씬 더 특별한 경우로, 모든 인접하지 않은 정점 쌍이 서로 [14]단위 거리보다 크다.
특성.
가장자리 수
Paul Erd's(1946)는 n개의\n개의 집합에서 서로 단위 거리에 몇 쌍의 포인트가 있을 수 있는지를 추정하는 문제를 제기했다.이 질문은 그래프 이론적인 용어로 단위 거리 그래프가 얼마나 조밀할 수 있는지를 묻는 것으로 표현될 수 있으며, 이 질문에 대한 Erds의 발표는 극단적 그래프 [15]이론의 첫 번째 연구 중 하나이다.하이퍼큐브 그래프와 해밍 그래프는 에 하는 단위 거리 수의 하한을 제공합니다.{ n n스페이스가 신중하게 선택된 정사각형 그리드의 점을 고려함으로써 Erd는 형식의 하한을 개선했습니다.
값 nn의 경우 가능한 정확한 최대 에지 수를 알 수 있습니다.n ,3,의 n 에지의 수는 다음과 같습니다.[18]
금지된 하위 그래프
엄격한 단위 거리 그래프 또는 단위 거리 그래프의 하위 그래프인 것은 유전적인 특성입니다. 즉, 어느 한 유형의 그래프의 유도 하위 그래프는 모두 동일한 유형의 그래프입니다.따라서 이러한 속성은 금지된 하위 그래프에 의해 설명될 수 있습니다. 유도된 하위 그래프가 속성에 대한 최소 반례를 포함하지 않는 경우에만 그래프는 이러한 속성 중 하나를 가집니다.완전한 K 4와 더불어 이러한 금지된 그래프에는 완전한 초당 ,3(\이 포함됩니다.이 그래프의 2개의 버텍스 쪽에 있는 정점이 배치되는 위치에 있는 경우 다른 3개의 정점이 배치될 수 있는 위치는 최대 2개입니다.d.[8] 이들은 최대 5개의 정점에 있는 단위 거리 그래프의 하위 그래프에 대해 유일하게 금지된 2개의 그래프이다. 최대 7개의[6] 정점에 6개의 금지된 그래프와 최대 9개의 정점에 74개의 금지된 그래프가 있다.두 개의 작은 단위 거리 그래프(또는 단위 거리 그래프의 하위 그래프)를 정점에 접착하여 형성된 그래프는 그 자체로 단위 거리 그래프이기 때문에 모든 금지된 그래프는 이 접착 [19]프로세스에서는 형성할 수 없는 쌍커넥티드 그래프입니다.
휠 7은 6개의 정점이 단위 정육각형이고 7번째 정육각형이 육각형의 중심에 있는 엄밀한 단위 거리 그래프로 구현될 수 있습니다.중심 정점에서 모서리 중 하나를 제거하면 단위 길이 모서리를 가지지만 정확한 단위 거리 그래프는 아닌 하위 그래프가 생성됩니다.정점의 정육각형 배치는 인접한 정점이 단위 거리만큼 떨어져 있는 다른 위치에 정점을 배치할 수 있는 유일한 방법이며, 이 배치는 누락된 모서리의 두 끝점을 단위 거리에 배치합니다.따라서 단위 거리 [20]그래프에 대해서는 금지된 그래프이지만 단위 거리 [19]그래프의 하위 그래프에 대해서는 금지된 6가지 그래프 중 하나가 아닙니다.
대수적 수와 강성
모든 대수적 수 α{\displaystyle \alpha} 들어, 그것은 vertices의 쌍 거리들은 단위 거리 그래프 G{G\displaystyle}G{G\displaystyle}의 모든 단위 거리 항의 .[21]에{\displaystyle \alpha}α을 찾을 수 있을 이는 Beckman–Quarles기 위해서는 유한한 버전을 내포한다.heorem: 서로 의 평면 내 임의의 두 점 q에 대해 p p를 하는 유한한 강체 단위 거리 그래프가 존재하며, 단위를 보존하는 평면의 변환은이 그래프의 ces는 p p와q 사이의 를 유지합니다. 완전한[22]Beckman-Quarles 정리에서는 단위 거리를 유지하는 유클리드 평면(또는 고차원 공간)의 변환은 일치뿐임을 나타냅니다.이를 나타내는 또 다른 방법은 정점이 평면의 모든 점이 되는 무한 단위 거리 그래프의 경우 모든 그래프 자기동형이 평면의 모든 거리를 유지하며 단위 [23]거리도 유지한다는 것입니다.
만약 \alpha가 단일성의 근이 아닌 계수 1의 대수적 α(\의 정수 조합은 단위 거리 그래프가 무한도인 복소수 가법군의 최종 생성 부분군을 형성한다.예를 들어, \alpha는 -- +1(\1의 2개의 복소근 중 하나로 선택될 수 있으며,[24] 4개의 생성기가 있는 무한도 단위 거리 그래프를 생성한다.
색칠
Hadwiger-Nelson 문제는 단위 거리 그래프의 색수, 특히 유클리드 평면의 모든 점에서 형성된 무한 단위 거리 그래프에 관한 것이다.de Bruijn-Erd's 정리에 따르면, 선택 공리를 가정하면, 이것은 유한 단위 거리 그래프의 가장 큰 색수를 요구하는 것과 같다.적절한 [25]색상으로 5가지 색상을 요구하는 단위 거리 그래프가 있으며, 모든 단위 거리 그래프는 최대 7가지 색상으로 [26]색칠할 수 있습니다.

Paul Erd's의 다른 질문에 답하면 삼각형이 없는 단위 거리 그래프에는 4가지 [27]색상이 필요할 수 있습니다.
열거
n vertices{\ n 4개의 레이블이 있는 정점에 (엄격한) 단위 거리 그래프의 수는 최대[2]
높은 차원으로의 일반화
단위 거리 그래프의 정의는 자연스럽게 고차원 유클리드 공간으로 일반화될 수 있다.3차원에서n개의 \n점의 거리 그래프는 의 3 { n개의 에지를 가지며, 서β {\}는 역아커만 [28]함수와 관련하여 매우 느리게 성장하는 함수이다.이 결과는 3차원 상대 근린 [29]그래프의 가장자리 수에 유사한 경계를 부여하는 데 사용될 수 있다.4차원 이상의 차원에서는 공통의 중심을 갖는 두 개의 수직원에 점을 배치함으로써 완전한 초당 그래프를 단위 거리 그래프로 나타낼 수 있으므로 단위 거리 그래프는 조밀한 [7]그래프가 될 수 있다.단위 거리 그래프의 열거 공식은 더 높은 차원으로 일반화되며, 4차원 이상의 엄격한 단위 거리 그래프의 수가 단위 거리 [2]그래프의 하위 그래프 수보다 훨씬 크다는 것을 보여준다.
모든 그래프는 충분히 높은 치수의 점 세트로 포함될 수 있다.모든 가장자리가 단위 거리를 가지도록 그래프를 삽입하는 데 필요한 치수와 가장자리가 정확히 단위 거리 쌍이 되도록 그래프를 삽입하는 데 필요한 치수는 서로 크게 다를 수 있습니다. 2n-vertex 크라운 그래프는 모든 가장자리의 단위 길이를 가지도록 4차원에 삽입할 수 있지만 n-2차원 이상이 필요합니다.단위가 유일한 단위-거리 [30]쌍이 되도록 삽입해야 합니다.그래프를 엄밀한 단위 그래프로 실현하는 데 필요한 치수는(가장자리를 정확히 단위 거리 쌍이 되도록 함) 최대 [31]두 배입니다.
계산의 복잡성
점으로부터 단위 거리 그래프를 구성하는 것은 더 큰 점 집합에서 일부 패턴의 일치된 복사본을 찾기 위한 다른 알고리즘의 중요한 단계입니다.이러한 알고리즘은 이 구성을 사용하여 패턴 내의 거리 중 하나가 존재하는 후보 위치를 검색하고 다른 방법을 사용하여 각 [32]후보에 대해 패턴의 나머지 부분을 테스트합니다.이 [32]문제에 대해 Matoushek(1993)의 방법을 적용할 수 있으며, 단위 거리 그래프의 가장자리를 n/3 n ) { n^ { 4 /} 2^ {*} 에서 구하는 알고리즘을 얻을 수 있습니다.서 log \ [33]^{*}는 로그함수입니다.
주어진 그래프가 단위 거리 그래프의 하위 그래프인지 또는 엄격한 단위 거리 [34]그래프인지를 테스트하는 것은 NP-hard이며, 특히 실존 실재 이론의 경우 더 완전하다.또한 그래프의 정점이 모두 정수 [35]좌표를 가지고 있는 경우에도 단위 거리 그래프에 해밀턴 사이클이 있는지 여부를 결정하는 것은 NP-완전입니다.
레퍼런스
메모들
- ^ 그리피스(2019).
- ^ a b c d Alon & Kupavskii (2014).
- ^ a b c d Gervacio, Lim & Maehara(2008).
- ^ a b 카미 등 (2008년).
- ^ Huson & Sen (1995).
- ^ a b Chilakamarri & Mahoney(1995).
- ^ a b Erdos, Harary & Tutte(1965).
- ^ a b Horvat & Pisanski (2010).
- ^ 브루어 & 해머(2012).
- ^ 에르데시스, 하라리 & 투트(1965년); 그리피스(2019년)
- ^ Gerbract (2009년)
- ^ Soifer (2008), 페이지 14-15, 19.
- ^ 지트니크, 호바트, 피산스키(2012).
- ^ a b Lavollée & Swaneboel (2022).
- ^ Szemerédi (2016).
- ^ 쿠퍼버그(1992)
- ^ Spencer, Szemerédi & Trotter(1984년), Clarkson 등(1990년), Pach & Tardos(2005년), Agoston & Palvölgyi(2022년)
- ^ Agoston & Palvölgyi (2022).
- ^ a b Globus & Parshall (2020년).
- ^ Soifer (2008), 페이지 94.
- ^ 마에하라(1991년, 1992년).
- ^ Tyszka(2000).
- ^ Beckman & Quarles(1953년).
- ^ 라드첸코(2021년).
- ^ Langin (2018년)
- ^ Soifer (2008), 17페이지.
- ^ Wormald(1979년), Chilakamarri(1995년), O'Donnell(1995년).
- ^ 클락슨 외 연구진(1990년)
- ^ Jaromczyk & Toussaint(1992)
- ^ Erdss & Simonovits(1980).
- ^ 마에하라 & 뢰들(1990).
- ^ a b 브라 ((2002년).
- ^ Matoushek(1993); 시간 )의 포인트 라인 발생을 나열하기 위한 밀접하게 관련된 알고리즘에 대해서는 Chan & Zheng(도 참조해
- ^ Shaefer(2013).
- ^ Itai, Papadimitriou & Swarcfiter(1982).
원천
- Ágoston, Péter; Pálvölgyi, Dömötör (April 2022), "An improved constant factor for the unit distance problem", Studia Scientiarum Mathematicarum Hungarica, Akademiai Kiado Zrt., 59 (1): 40–57, arXiv:2006.06285, doi:10.1556/012.2022.01517
- Alon, Noga; Kupavskii, Andrey (2014), "Two notions of unit distance graphs" (PDF), Journal of Combinatorial Theory, Series A, 125: 1–17, doi:10.1016/j.jcta.2014.02.006, MR 3207464
- Beckman, F. S.; Quarles, D. A., Jr. (1953), "On isometries of Euclidean spaces", Proceedings of the American Mathematical Society, 4 (5): 810–815, doi:10.2307/2032415, JSTOR 2032415, MR 0058193
- Braß, Peter (2002), "Combinatorial geometry problems in pattern recognition", Discrete & Computational Geometry, 28 (4): 495–510, doi:10.1007/s00454-002-2884-3, MR 1949897
- Brouwer, Andries E.; Haemers, Willem H. (2012), Spectra of Graphs, Universitext, New York: Springer, p. 178, doi:10.1007/978-1-4614-1939-6, ISBN 978-1-4614-1938-9, MR 2882891
- Carmi, Paz; Dujmović, Vida; Morin, Pat; Wood, David R. (2008), "Distinct distances in graph drawings", Electronic Journal of Combinatorics, 15 (1): Research Paper 107, arXiv:0804.3690, MR 2438579
- Chan, Timothy M.; Zheng, Da Wei (2022), "Hopcroft's problem, log-star shaving, 2d fractional cascading, and decision trees", in Naor, Joseph (Seffi); Buchbinder, Niv (eds.), Proceedings of the 2022 ACM-SIAM Symposium on Discrete Algorithms, SODA 2022, Virtual Conference / Alexandria, VA, USA, January 9 - 12, 2022, Society for Industrial and Applied Mathematics, pp. 190–210, arXiv:2111.03744, doi:10.1137/1.9781611977073.10
- Chilakamarri, Kiran B. (1995), "A 4-chromatic unit-distance graph with no triangles", Geombinatorics, 4 (3): 64–76, MR 1313386
- Globus & Parshall (2020)에서 인용한Chilakamarri, Kiran B.; Mahoney, Carolyn R. (1995), "Maximal and minimal forbidden unit-distance graphs in the plane", Bulletin of the Institute of Combinatorics and its Applications, 13: 35–43, MR 1314500 바와 같이
- Clarkson, Kenneth L.; Edelsbrunner, Herbert; Guibas, Leonidas J.; Sharir, Micha; Welzl, Emo (1990), "Combinatorial complexity bounds for arrangements of curves and spheres", Discrete & Computational Geometry, 5 (2): 99–160, doi:10.1007/BF02187783, MR 1032370
- Erdős, Paul (1946), "On sets of distances of points", American Mathematical Monthly, 53 (5): 248–250, doi:10.2307/2305092, JSTOR 2305092
- Erdős, Paul; Harary, Frank; Tutte, William T. (1965), "On the dimension of a graph" (PDF), Mathematika, 12: 118–122, doi:10.1112/S0025579300005222, hdl:2027.42/152495, MR 0188096
- Soifer(2008년, 페이지 97Erdős, Paul; Simonovits, Miklós (1980), "On the chromatic number of geometric graphs", Ars Combinatoria, 9: 229–246)가 인용한 바와 같이
- Gerbracht, Eberhard H.-A. (2009), Eleven unit distance embeddings of the Heawood graph, arXiv:0912.5395, Bibcode:2009arXiv0912.5395G
- Gervacio, Severino V.; Lim, Yvette F.; Maehara, Hiroshi (2008), "Planar unit-distance graphs having planar unit-distance complement", Discrete Mathematics, 308 (10): 1973–1984, doi:10.1016/j.disc.2007.04.050
- Globus, Aidan; Parshall, Hans (2020), "Small unit-distance graphs in the plane", Bulletin of the Institute of Combinatorics and its Applications, 90: 107–138, arXiv:1905.07829, MR 4156400
- Griffiths, Martin (June 2019), "103.27 A property of a particular unit-distance graph", The Mathematical Gazette, 103 (557): 353–356, doi:10.1017/mag.2019.74
- Horvat, Boris; Pisanski, Tomaž (2010), "Products of unit distance graphs", Discrete Mathematics, 310 (12): 1783–1792, doi:10.1016/j.disc.2009.11.035, MR 2610282
- Huson, Mark L.; Sen, Arunabha (1995), "Broadcast scheduling algorithms for radio networks", Military Communications Conference, IEEE MILCOM '95, vol. 2, pp. 647–651, doi:10.1109/MILCOM.1995.483546, ISBN 0-7803-2489-7
- Itai, Alon; Papadimitriou, Christos H.; Szwarcfiter, Jayme Luiz (1982), "Hamilton paths in grid graphs", SIAM Journal on Computing, 11 (4): 676–686, CiteSeerX 10.1.1.383.1078, doi:10.1137/0211056, MR 0677661
- Jaromczyk, Jerzy W.; Toussaint, Godfried T. (1992), "Relative neighborhood graphs and their relatives", Proceedings of the IEEE, 80 (9): 1502–1517, doi:10.1109/5.163414
- Kuperberg, Greg (1992), The Erdos kitty: At least $9050 in prizes!, Posting to usenet groups rec.puzzles and sci.math, archived from the original on 2006-09-29
- Langin, Katie (April 18, 2018), "Amateur mathematician cracks decades-old math problem", Science
- Lavollée, Jérémy; Swanepoel, Konrad J. (2022), "Bounding the number of edges of matchstick graphs", SIAM Journal on Discrete Mathematics, 36 (1): 777–785, arXiv:2108.07522, doi:10.1137/21M1441134, MR 4399020
- Maehara, Hiroshi (1991), "Distances in a rigid unit-distance graph in the plane", Discrete Applied Mathematics, 31 (2): 193–200, doi:10.1016/0166-218X(91)90070-D
- Maehara, Hiroshi (1992), "Extending a flexible unit-bar framework to a rigid one", Discrete Mathematics, 108 (1–3): 167–174, doi:10.1016/0012-365X(92)90671-2, MR 1189840
- Maehara, Hiroshi; Rödl, Vojtech (1990), "On the dimension to represent a graph by a unit distance graph", Graphs and Combinatorics, 6 (4): 365–367, doi:10.1007/BF01787703
- Matoušek, Jiří (1993), "Range searching with efficient hierarchical cuttings", Discrete & Computational Geometry, 10 (2): 157–182, doi:10.1007/BF02573972, MR 1220545
- O'Donnell, Paul (1995), "A 40 vertex 4-chromatic triangle-free unit distance graph", Geombinatorics, 5 (1): 31–34, MR 1337155
- Pach, János; Tardos, Gábor (2005), "Forbidden patterns and unit distances", in Mitchell, Joseph S. B.; Rote, Günter (eds.), Proceedings of the 21st ACM Symposium on Computational Geometry, Pisa, Italy, June 6-8, 2005, Association for Computing Machinery, pp. 1–9, doi:10.1145/1064092.1064096, MR 2460341
- Radchenko, Danylo (2021), "Unit distance graphs and algebraic integers", Discrete & Computational Geometry, 66 (1): 269–272, doi:10.1007/s00454-019-00152-4, MR 4270642
- Schaefer, Marcus (2013), "Realizability of graphs and linkages", in Pach, János (ed.), Thirty Essays on Geometric Graph Theory, Springer, pp. 461–482, CiteSeerX 10.1.1.220.9651, doi:10.1007/978-1-4614-0110-0_24, ISBN 978-1-4614-0109-4
- Soifer, Alexander (2008), The Mathematical Coloring Book, Springer-Verlag, ISBN 978-0-387-74640-1
- Spencer, Joel; Szemerédi, Endre; Trotter, William T. (1984), "Unit distances in the Euclidean plane", in Bollobás, Béla (ed.), Graph Theory and Combinatorics, London: Academic Press, pp. 293–308, ISBN 978-0-12-111760-3, MR 0777185
- Szemerédi, Endre (2016), "Erdős's unit distance problem", in Nash, John Forbes, Jr.; Rassias, Michael Th. (eds.), Open Problems in Mathematics, Cham, Switzerland: Springer, pp. 459–477, doi:10.1007/978-3-319-32162-2_15, MR 3526946
- Tyszka, Apoloniusz (2000), "Discrete versions of the Beckman-Quarles theorem", Aequationes Mathematicae, 59 (1–2): 124–133, arXiv:math/9904047, doi:10.1007/PL00000119, MR 1741475
- Wormald, Nicholas (1979), "A 4-chromatic graph with a special plane drawing", Journal of the Australian Mathematical Society, Series A, 28 (1): 1–8, MR 0541161
- Žitnik, Arjana; Horvat, Boris; Pisanski, Tomaž (2012), "All generalized Petersen graphs are unit-distance graphs", Journal of the Korean Mathematical Society, 49 (3): 475–491, doi:10.4134/JKMS.2012.49.3.475, MR 2953031
외부 링크
- Venkatasubramanian, Suresh, "Problem 39: Distances among Point Sets in R2 and R3", The Open Problems Project
- Weisstein, Eric W., "Unit-Distance Graph", MathWorld

 몇 개의 모서리를 가질 수 있는지 알 수 없습니다.
몇 개의 모서리를 가질 수 있는지 알 수 없습니다. 


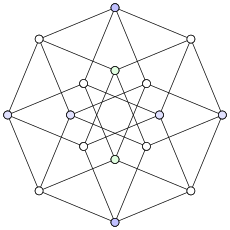
 16개의 정점과 32개의 단위 거리가 있습니다.
16개의 정점과 32개의 단위 거리가 있습니다.










 평면
평면









