골롬 그래프
Golomb graph| 골롬 그래프 | |
|---|---|
 | |
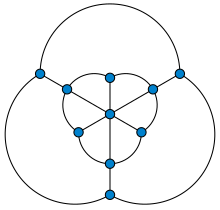| 이름을 따서 명명됨 | 솔로몬 W. 골롬 |
| 정점 | 10 |
| 가장자리 | 18 |
| 자동형성 | 6 |
| 색수 | 4 |
| 특성. | |
| 그래프 및 모수 표 | |
그래프 이론에서 골롬 그래프는 정점이 10개, 가장자리가 18개인 다면 그래프다.어떤 그래프 컬러링에도 4가지 색상이 필요한 단위 거리 그래프로 (비평면 임베딩으로) 시공한 솔로몬 W.골롬의 이름을 따서 지은 이름이다.따라서 보다 단순한 Moser 스핀들과 마찬가지로 Hadwiger-Nelson 문제에 대한 하한선을 제공한다. 즉, 유클리드 평면의 점들을 색칠하여 각 단위 라인 세그먼트의 색상이 다르도록 하기 위해서는 적어도 4가지 색상이 필요하다.[1]
건설
내부 트위스트 폴리곤이나 별 폴리곤에 연결된 외부 일반 폴리곤을 그려 단위 거리 그래프로 골롬 그래프를 구성하는 방법도 피터슨 그래프의 단위 거리 표현과 일반화된 피터슨 그래프의 단위 거리 표현에 사용되었다.[2]Moser 스핀들과 마찬가지로 Golomb 그래프의 단위 거리 내장 좌표는 2차 Q[ 에 나타낼 수 있다[3]
![{\displaystyle \mathbb {Q} [{\sqrt {33}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b920b3da2daef8f7f2ff1cbc6618b2ad08963bd)
분수색소
Golomb 그래프의 소수 색수는 10/3이다.이 숫자가 적어도 이만큼 크다는 사실은 그래프가 10개의 정점을 가지고 있다는 사실에서 따르며, 그 중 적어도 3개는 독립 집합에 있을 수 있다.그 숫자가 기껏해야 이만큼 크다는 사실은 각 꼭지점이 정확히 세 개 안에 들어 있을 정도로 세 개의 베르테스 독립 세트를 10개 찾을 수 있다는 사실에서 따온 것이다.이 분수 색도 번호는 Moser 스핀들에 대한 숫자 7/2보다 작으며 3.6190과 4.3599 사이의 경계인 평면의 단위 거리 그래프의 분수 색도 번호보다 작다.[4]
참조
- ^ Soifer, Alexander (2008), The Mathematical Coloring Book: Mathematics of Coloring and the Colorful Life of its Creators, New York: Springer, p. 19, ISBN 978-0-387-74640-1
- ^ Žitnik, Arjana; Horvat, Boris; Pisanski, Tomaž (2012), "All generalized Petersen graphs are unit-distance graphs", Journal of the Korean Mathematical Society, 49 (3): 475–491, doi:10.4134/JKMS.2012.49.3.475, MR 2953031
- ^ Pegg, Ed, Jr. (December 21, 2017), "Moser Spindles, Golomb Graphs and Root 33", Wolfram Demonstrations Project
- ^ Cranston, Daniel W.; Rabern, Landon (2017), "The fractional chromatic number of the plane", Combinatorica, 37 (5): 837–861, arXiv:1501.01647, doi:10.1007/s00493-016-3380-3, MR 3737371, S2CID 4687673
