탯줄 포인트

3차원의 표면의 차등 기하학에서, 탯줄이나 탯줄 점은 국소적으로 구형인 표면의 점들이다. 그러한 점에서 모든 방향의 정상 곡선은 동일하므로, 두 원곡선은 모두 동일하며, 모든 접선 벡터는 주 방향이다. "umbilic"이라는 이름은 라틴어 umbilicus (navel)에서 유래되었다.

탯줄 점들은 일반적으로 표면의 타원형 영역에서 격리된 점으로 발생한다. 즉, 가우스 곡면성이 양수인 경우.

구는 모든 점이 탯줄로 되어 있는 0이 아닌 곡률을 가진 유일한 표면이다. 납작한 탯줄은 가우스 곡률이 0인 탯줄이다. 원숭이 안장은 평평한 탯줄이 있는 표면의 한 예로서 평면에는 모든 점이 평평한 탯줄이 있다. 토러스에는 탯줄이 없지만 유클리드 공간에 매끄럽게 박혀 있는 0이 아닌 오일러 특성의 모든 닫힌 표면에는 적어도 1개의 탯줄이 있다. 콘스탄틴 캐러테오도리에 대한 입증되지 않은 추측에 따르면 유클리드 공간의 모든 매끄러운 위상학 영역에는 적어도 두 개의 탯줄이 있다고 한다.^[1]

탯줄 포인트의 세 가지 주요 유형은 타원형 탯줄, 포물선 탯줄, 쌍곡선 탯줄이다. 타원형 탯줄은 탯줄을 통과하는 3개의 능선이 있고 쌍곡선 탯줄은 1개만 있다. 포물선 탯줄은 두 개의 능선이 있는 과도기적인 경우로 그 중 하나는 단수적이다. 과도기적인 경우에 다른 구성이 가능하다. 이 사건들은 르네 톰의 재난 이론의₄⁻ D, D₅, D의₄⁺ 기본적인 재난에 해당한다.

또한 탯줄은 일반적으로 별, 레몬, 레몬 별(또는 몬스타)의 세 가지 구성 중 하나를 이루는 탯줄 주위의 주 방향 벡터 필드의 패턴에 의해 특징지어질 수 있다. 벡터 필드의 지수는 - -(별) 또는 ½(레몬, 몬스타)이다. 타원형 탯줄과 포물선 탯줄은 항성 패턴을 항상 가지고 있는 반면, 쌍곡선 탯줄은 항성, 레몬, 몬스타가 될 수 있다. 이 분류는 Darboux에 의한 것이고 이름은 Hannay에서 유래되었다.^[2]

고립된 탯줄이 있는 0 속 표면(예: 타원체)의 경우, 원칙 방향 벡터 필드의 지수는 푸앵카레-홉프 정리에 의해 2가 되어야 한다. 일반 속 0 표면은 지수 ½의 최소 4개의 탯줄을 가지고 있다. 혁명의 타원체에는 각각 지수 1을 갖는 두 개의 비장성 탯줄이 있다.^[3]

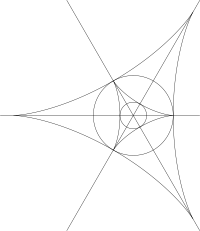
• 탯줄 근처의 곡률선 구성
• 

  별

• 

  몬스타

• 

  레몬

탯줄 분류

입방형식

The classification of umbilics is closely linked to the classification of real cubic forms ${\displaystyle ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3}}$. A cubic form will have a number of root lines ${\displaystyle \lambda (x,y)}$ such that the cubic form is zero for all real ${\displaystyle \lambda }$$다음$과 같은 여러 가지 가능성이 있다$.$

• 세 개의 구별되는 선: 타원형 입방형, 표준 모델 $x{\displaystyle {}^{}}$ ${\displaystyle {}^{}}$- ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}${\$displaystyle$ x$^{$2}$y-y^{3$
• 세 개의 선, 그 중 두 개의 선: 포물선 입방형, $표준{\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ x 2 y ${\displaystyle x^{$2}$y$
• 단일 실선: 쌍곡선 입방형, 표준 모델 $x{\displaystyle {}^{}}$ ${\displaystyle {}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\$ x$^{2}y+y^{3$
• 세 개의 일치선, 표준 모델 ${\displaystyle {x\mathrm{}}^{}}$ 3 ${\$ x$^{3$^[4]

균일한 스케일 하에서 그러한 큐빅의 등가 등급은 3차원 실제 투영 공간을 형성하고 포물선 형태의 부분집합은 표면을 정의하는데 크리스토퍼 지만이 탯줄 팔찌라고 부른다.^[4] Taking equivalence classes under rotation of the coordinate system removes one further parameter and a cubic forms can be represent by the complex cubic form ${\displaystyle z^{3}+3{\overline {\beta }}z^{2}{\overline {z}}+3\beta z{\overline {z}}^{2}+{\overline {z}}^{3}}$$$ with a single complex parameter ${\displaystyle \beta }$. Parabolic forms occur when ${\displaystyle \beta ={\tfrac {1}{3}}(2e^{i\theta }+e^{-2i\theta })}$, the inner deltoid, elliptical forms are inside the deltoid and hyperbolic one outside. ${\displaystyle \beta }$= ${\displaystyle 1}$ ${\displaystyle \left \beta \right =$1$}$및 $\beta {\displaystyle }$ ${\displaystyle \beta }$이(가) 통합의 큐브 루트가 아니라면$$ 입방 형태는 탯줄에 특별한 역할을 하는 직각 입방 형태다. ${\displaystyle \beta }$= ${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{3}{}}$ ${\$인 경우 루트 라인 중 두 개가 직교하는 것이다$$.^[5]

A second cubic form, the Jacobian is formed by taking the Jacobian determinant of the vector valued function ${\displaystyle F:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}}$, ${\displaystyle F(x,y)=(x^{2}+y^{2},ax^{3}+3b$$x^{2}y+3cxy^{2}+dy^{3})}$. Up to a constant multiple this is the cubic form ${\displaystyle bx^{3}+(2c-a)x^{2}y+(d-2b)xy^{2}-cy^{3}}$. Using complex numbers the Jacobian is a parabolic cubic form when ${\displaystyle \beta =-2e^{i\the$$ta }-e^{-2i\theta }},$ 분류 다이어그램의 바깥쪽 델토이드$.$^[5]

탯줄 분류

Any surface with an isolated umbilic point at the origin can be expressed as a Monge form parameterisation ${\displaystyle z={\tfrac {1}{2}}\kappa (x^{2}+y^{2})+{\tfrac {1}{3}}(ax^{3}+3bx^{2}y+3cxy^{2}+dy^{3})+\ldots }$, where ${\displaystyle \kappa }$${\displaystyle }$고유한$$ 주 곡면성이 바로 ${\displaystyle \kappa }$ 탯줄의 종류는 입방체에서 입방체로 분류되며, 이에 상응하는 자코비안 입방체로 분류된다. 주 방향은 탯줄에서 고유하게 정의되지 않지만, 표면의 능선을 따라갈 때 주 방향의 한계를 발견할 수 있으며, 이는 입방형식의 루트 라인에 해당한다. 곡률 선들의 패턴은 자코비안에 의해 결정된다.^[5]

탯줄 점의 분류는 다음과 같다.^[5]

• 내부 델토이드 - 타원형 탯줄 내부
  • 내부 원 - 접선되는 두 개의 능선
• 내부 델토이드 포물선 탯줄에 대하여
• 내부 델토이드 외부 - 쌍곡선 탯줄
  • 외부 원 내부 - 별 패턴
  • 외계에서 - 탯줄의 탄생
  • 외부 원과 외부 델토이드 사이 - 몬스타 패턴
  • 외부 델토이드 - 레몬 패턴
• 내부 델토이드 큐빅(심볼릭) 탯줄의 큐스
• 대각선 및 수평선 - 거울 대칭이 있는 대칭 탯줄

일반적인 표면 제품군에서 탯줄은 쌍으로 생성되거나 파괴될 수 있다: 탯줄 전환의 탄생. 두 탯줄 모두 쌍곡선이며, 하나는 별무늬가 있고 다른 하나는 몬스타무늬가 있을 것이다. 다이어그램의 바깥 원, 직각 입방 형태는 이러한 과도기적인 경우를 제시한다. 상징적인 탯줄은 이것의 특별한 경우다.^[5]

초점면

타원형 탯줄과 쌍곡선 탯줄은 초점 표면이 확연히 다르다. 표면의 능선은 가장자리에 해당하므로 타원 초점 표면의 각 시트에는 세 개의 가장자리가 있으며, 이 가장자리는 탯줄 초점에서 결합한 후 다른 시트로 전환된다. 쌍곡선 탯줄의 경우 한 시트에서 다른 시트로 전환되는 단일 가장자리가 있다.^[5]

리만 다양체에서 더 높은 차원의 정의

리만니안 하위 매니폴드의 p점은 p에서 (벡터 값) 두 번째 기본 형태는 유도 미터법(첫 번째 기본 형태)의 어떤 정상 벡터 텐서일 경우 탯줄이다. 동등하게 모든 벡터 U, V at p, II(U, V) = g_p(U, V) ${\displaystyle }$ ${\displaystyle \nu$ 여기서 $\nu {\displaystyle }$ ${\displaystyle \nu}$은 p의 평균 곡률 벡터다.

서브매니폴드는 이 상태가 모든 지점 "p"에서 유지되면 탯줄(또는 모든 음부)이라고 한다. 이는 주변("주변") 다지관의 측정기준을 적절히 변경하여 서브매니폴드를 완전히 지오디컬로 만들 수 있다고 말하는 것과 같다. 예를 들어 유클리드 공간의 표면은 구의 한 조각일 경우에만 탯줄로 되어 있다.

참고 항목

• 탯줄 – 배꼽의 의미 또는 이와 관련된 해부학적 용어
• 캐러테오도리 추측

참조

• Darboux, Gaston (1887,1889,1896), Leçons sur la théorie génerale des surfaces: Volume I, Volume II, Volume III, Volume IV, Gauthier-Villars 날짜 값 확인: year= (도움말); 외부 링크 위치 title= (도움말)
• 별, 레몬, 몬스타 및 추가 참조 사진