셸 밸런스

이 글에는 여러 가지 문제가 있다.이 문제를 개선하거나 대화 페이지에서 토의하십시오.(이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글에는 참고문헌, 관련 독서 또는 외부 링크 목록이 수록되어 있으나 인라인 인용구가 부족하여 출처가 불분명하다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2020년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) 이 기사의 주제는 위키피디아의 일반적인 공신력 가이드라인을 충족하지 못할 수 있다. 주제와 무관하고 사소한 언급 이상의 중요한 내용을 제공하는 신뢰할 수 있는 2차 소스를 인용함으로써 주제의 공신력을 증명할 수 있도록 도와주십시오. 공지를 표시할 수 없는 경우, 기사는 병합, 리디렉션 또는 삭제될 가능성이 높다. 출처 찾기: "Shell balance" – 뉴스 · 신문 · 책 · 학자 · JSTOR(2020년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 학습) 이 글은 특정 청중에게만 관심을 가질 수 있는 과도한 양의 복잡한 세부사항을 포함할 수 있다. 관련 정보를 줄이거나 재배치하고 위키피디아의 포함 정책에 위배될 수 있는 과도한 세부사항을 제거하여 도움을 요청하십시오.(2020년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

유체 역학에서, 조개 균형은 유체 속도가 흐름에서 어떻게 변화하는지 결정하는 데 사용될 수 있다.

껍데기는 흐름의 차등 요소다.하나의 작은 부분에 대한 운동량과 힘을 보면 흐름 위로 통합되어 흐름 전체의 큰 그림을 볼 수 있다.균형이 껍데기에 들어가고 나오는 것을 결정하는 것이다.탄력은 쉘에 들어오고 나가는 유체와 전단 응력을 통해 쉘 내에서 생성된다.게다가 껍질에는 압력과 중력이 있다.쉘 밸런스의 목적은 흐름의 속도 프로파일을 결정하는 것이다.속도 프로파일은 흐름의 특정 위치를 기준으로 속도를 계산하는 방정식이다.이를 통해 흐름을 가로지르는 어떤 지점의 속도도 찾을 수 있다.

적용들

Shell Balance는 많은 상황에서 사용될 수 있다.예를 들어, 파이프 안의 흐름, 여러 유체의 흐름, 또는 압력 차이로 인한 흐름.껍질 균형과 경계 조건의 용어는 변경되겠지만 기본 설정과 과정은 동일하다.

쉘 밸런스 계산 요구 사항

오일은 다음을 나타내야 한다.

• 층류 흐름
• 커브 또는 커브 없음
• 안정화 상태
• 두 경계 조건

경계 조건은 통합의 상수를 찾는 데 사용된다.

• 유체 - 고체 경계: 미끄럼 방지 조건, 고형에서 액체의 속도는 고형물의 속도와 동일하다.
• 액체 - 가스 경계:전단 응력 = 0.
• 액체 - 액체 경계: 두 액체의 동일한 속도 및 전단 응력

셸 밸런스 수행 중

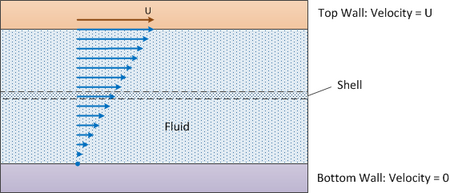
접촉 영역 A의 두 수평 표면 사이에 오일이 흐르고 있다.높이 Δy의 차동 쉘을 사용한다(아래 다이어그램 참조).

상단 표면은 속도 U에서 움직이고 하단 표면은 정지해 있다.

• 유체 밀도 = ρ
• 유체의 점성 = μ
• x 방향의 속도 = $V{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$ 위의 대각선으로 표시됨.이것이 바로 껍데기 균형이 해결되는 것이다.

모멘텀 보존이 쉘 밸런스의 핵심

• (운동량 비율) - (운동량 배출 속도) + (모든 힘의 합계) = 0

셸 밸런싱을 수행하려면 다음 기본 단계를 수행하십시오.

1. 전단 응력에서 운동량을 찾는다.(전단 응력에서 시스템으로의 모멘텀) - (전단 응력에서 시스템 밖으로의 모멘텀).전단 응력으로부터의 모멘텀은 y에서 쉘 안으로 들어가 y + Δy에서 시스템을 떠난다.전단 응력 = τ_yx, 면적 = A, 운동량 = τA_yx.
2. 흐름에서 추진력을 찾으십시오.모멘텀은 x = 0에서 시스템으로 유입되고 x = L에서 흘러나온다.흐름이 안정되어 있다.따라서 x = 0에서의 모멘텀 흐름은 x = L에서의 모멘트와 동일하다.그러므로, 이것들은 취소된다.
3. 껍질에서 중력을 찾아라.
4. 압력력을 찾아라.
5. 모멘텀 보존에 플러그를 꽂아 τ을_yx 해결한다.
6. 뉴턴 유체 τ_yx = -μ(dV_x/dy)에 뉴턴의 점성 법칙을 적용한다.
7. 적분하여 속도에 대한 방정식을 찾고, 적분 상수를 찾으려면 경계 조건을 사용하십시오.

경계 1: 상단 표면: y = 0 및 V = U_x

경계 2: 아래쪽 표면: y = D 및 V = 0_x

셸 밸런스 수행 예제를 보려면 아래 나열된 리소스를 방문하십시오.

자원.

• "Problem Solutions in Transport Phenomena : Fluid Mechanics Problems". Retrieved 2007-10-06.

• Harriott, Peter; W. McCabe; J. Smith (2004). Unit Operations of Chemical Engineering: Seventh Edition. McGraw-Hill Professional. pp. 68–132. ISBN 9780072848236.