포물선 반사경
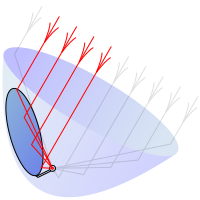
Parabolic reflector포물선(또는 포물선 또는 포물선) 반사체(또는 접시 또는 거울)는 빛, 소리 또는 전파와 같은 에너지를 수집하거나 투영하는 데 사용되는 반사 표면입니다.그 모양은 원형 포물선의 일부, 즉 포물선이 축을 중심으로 회전하면서 생기는 표면이다.포물선 반사기는 축을 따라 이동하는 들어오는 평면파를 포커스를 향해 수렴하는 구형파로 변환합니다.반대로 초점에 배치된 점원에 의해 발생한 구형파는 축을 따라 시준빔으로 전파되는 평면파에 반사된다.
포물선 반사기는 먼 소스(예: 음파 또는 들어오는 별 빛)로부터 에너지를 모으는 데 사용됩니다.반사의 원리는 가역적이기 때문에 포물선 반사기를 사용하여 등방성 선원의 방사선을 평행 [1]빔으로 콜리메이트할 수도 있다.광학에서, 포물선 거울은 반사 망원경과 태양로에 빛을 모으고, 손전등, 서치라이트, 무대 스포트라이트, 자동차 헤드라이트에 빛을 투사하는 데 사용됩니다.무선에서 포물선 안테나는 위성 접시 및 마이크로파 중계소에서 지점 간 통신을 위해 좁은 전파 빔을 방사하고 레이더 세트의 항공기, 선박 및 차량을 찾기 위해 사용된다.음향학에서는 포물선 마이크가 버드 울음소리, 스포츠 리포팅, 스파이 활동 및 법 집행 기관의 사적인 대화를 도청하는 데 사용됩니다.
이론.
이 섹션은 어떠한 출처도 인용하지 않습니다.2012년 11월 (이의 방법과 합니다) |
엄밀히 말하면, 반사체의 3차원 형상을 포물선이라고 합니다.포물선은 2차원 도형이다. (구(球)와 원의 구별과 같다.)그러나, 비공식 언어에서, 포물선과 포물선 대신 포물선이라는 단어와 관련된 형용사 포물선이 종종 포물선과 포물선 대신 포물선이 사용된다.
포물선이 원점에 정점이 있고 Y축을 따라 대칭 축이 있는 데카르트 좌표에 위치하여 포물선이 위로 열린 경우, 포물선은 f (\\2이며 서 f {\ \f}는 포물선의 초점 길이이다(Parabola# 참조).데카르트 좌표계"에서)이에 대응하여 대칭 포물면 접시의 치수는 2,{\ \ 4FD 서F {\ \ F는 초점거리, D {\ \scriptstyle D는 접시 깊이(V의 대칭축에 따른 길이)로 대응한다.ertex) 및 R은 중앙에서 접시의 반지름입니다.반지름, 초점 및 깊이에 사용되는 모든 단위는 동일해야 합니다.이 세 가지 양 중 두 가지를 알고 있는 경우 이 방정식을 사용하여 세 번째 양을 계산할 수 있습니다.
표면을 따라 측정된 접시의 직경을 찾으려면 더 복잡한 계산이 필요합니다.이것은 때때로 "선형 직경"이라고 불리며, 납작하고 둥근 재료, 보통 금속의 직경과 같으며, 접시를 만들기 위해 자르고 구부릴 수 있는 적절한 크기입니다.계산에는 {\ P (또는 동등한 값: 2 P=}}{2D Q \ style QScriptstyle의 두 가지 중간 결과가 유용합니다 F 및 R \displaystyle R은 위와 같이 정의됩니다.으로 표면을 따라 측정된 접시의 직경은 R P + ( + P) ,\ { } { P} +\ \ ( { \{ R + Q } { } \right )로 지정됩니다ln ( \ frac { R + \ script )밑수 "e"에 대한 로그입니다.
접시의 부피는 와 같이 정의된 1, {\ \}\로 지정됩니다.이는반구 † \\ R} D \2}{2} 서의 볼륨 공식과 비교할 수 있습니다} \2})는 접시의 조리개 면적으로, 테두리로 둘러싸인 면적으로, 반사 접시가 차단할 수 있는 햇빛의 양에 비례한다접시의 오목면적은 A 2( (2 + D) 3/ - 3 ){ A2}\left(R^2+2)인 의 면적식을 사용하여 구할 수 있다. D 0 입니다.접시에 반사되는 빛의 비율은 초점 광원에서 1 R - \ - { \ \ { R } { \ pi 서F, \ style F, } { \ } D - style R。
포물선 반사기는 포물선 모양의 기하학적 특성 때문에 기능합니다. 접시의 축에 평행한 입사 광선은 중심점, 즉 "초점"에 반사됩니다(기하학적 증거는 여기를 클릭하십시오).많은 유형의 에너지가 이러한 방식으로 반사될 수 있기 때문에 포물선 반사기는 반사기로 들어가는 에너지를 특정 각도로 모으고 집중시키는 데 사용될 수 있다.마찬가지로 포커스에서 접시로 방사되는 에너지는 접시의 축에 평행한 빔으로 외부로 전달될 수 있다.
빔 직경과 초점 거리의 비율이 커질수록 강해지는 구형 수차를 겪는 구형 반사체와 달리 포물선 반사체를 임의의 폭의 빔에 수용시킬 수 있다.그러나 들어오는 빔이 축과 0이 아닌 각도를 만드는 경우(또는 방출점 소스가 포커스에 배치되지 않은 경우) 포물선 반사기는 혼수라고 하는 수차를 겪습니다.대부분의 다른 애플리케이션은 포물선의 축에서 벗어난 날카로운 분해능을 필요로 하지 않기 때문에 망원경에서 주로 이 점이 관심을 끈다.
에너지를 잘 집중시키기 위해 포물선 접시가 만들어져야 하는 정밀도는 에너지의 파장에 따라 달라집니다.만약 접시가 파장의 4분의 1만큼 틀리면, 반사된 에너지는 반파장만큼 틀리게 되는데, 이것은 접시의 다른 부분에서 적절하게 반사된 에너지를 파괴적으로 간섭하게 된다는 것을 의미한다.이를 방지하려면 접시가 약 30cm 이내로 올바르게 만들어져야 합니다.파장의 20분의 1가시광선의 파장 범위는 약 400~700나노미터(nm)이기 때문에 모든 가시광선의 초점을 잘 맞추려면 반사경이 약 20nm 이내로 정확해야 한다.비교하자면, 인간의 머리카락 지름은 보통 약 50,000 nm이기 때문에 반사경이 가시광선을 집중시키는 데 필요한 정확도는 머리카락 지름의 약 2500배입니다.예를 들어, 허블 우주 망원경 거울의 결함(주변에서 약 2,200 nm가 너무 평평함)은 [2]COSTAR로 수정되기 전까지 심각한 구면 수차를 유발했습니다.
위성 TV 신호에 사용되는 전자파는 10밀리미터의 파장을 가지고 있기 때문에, 이러한 파장의 초점을 맞추기 위한 접시는 0.5밀리미터 정도 어긋나면서도 성능이 양호합니다.
바리에이션
포커스 밸런스 리플렉터

반사 접시의 질량 중심이 초점과 일치할 경우 유용할 수 있습니다.이것은 목표물이 있는 곳에 초점이 고정되어 있는 동안 하늘의 태양과 같은 움직이는 광원을 겨냥할 수 있도록 쉽게 방향을 바꿀 수 있게 해준다.접시는 초점을 통과하고 균형을 이루는 축을 중심으로 회전합니다.접시가 대칭이고 일정한 두께의 균일한 재료로 구성되어 있으며, F가 포물체의 초점거리를 나타내는 경우, 포물체의 축을 따라 측정되는 깊이가 접시의 정점에서 테두리 면까지의 화씨 1.8478배일 경우, 이 "초점균형" 상태가 발생한다.림의 반지름은 [a]2.7187F입니다.초점에서 볼 때 림의 각 반지름은 72.68도입니다.
셰플러 반사경
포커스 밸런스 구성(위 참조)에서는 반사 접시의 깊이가 초점 거리보다 커야 하므로 포커스가 접시 안에 있습니다.이로 인해 포커스에 접근하기 어려울 수 있습니다.대안적 접근법은 발명가인 볼프강 셰플러의 이름을 딴 셰플러 반사체에 의해 예시된다.이것은 질량 중심을 통과하는 축을 중심으로 회전하는 포물면 거울이지만, 접시 바깥의 초점과 일치하지 않습니다.반사경이 단단한 포물면 접시가 회전할 때 초점이 움직입니다.이를 피하기 위해 반사경은 유연하고 회전할 때 구부러져 포커스를 정지시킨다.이상적으로는 반사경은 항상 정확하게 포물선 모양이어야 합니다.실제로는 정확하게 달성할 수 없기 때문에 셰플러 리플렉터는 높은 정밀도를 필요로 하는 목적에 적합하지 않습니다.태양광 조리 등 조리 냄비에 햇빛이 충분히 집중되어야 하지만 정확한 지점까지는 [3]그렇지 않은 용도로 사용됩니다.
축외 리플렉터
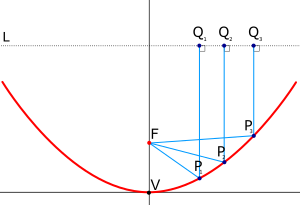
원형 포물체는 이론적으로 크기가 무한하다.모든 실제 반사경은 그것의 일부만을 사용합니다.종종 세그먼트는 포물체의 정점을 포함하는데, 포물체의 곡률이 가장 크고 대칭축이 포물체와 교차하는 곳이다.그러나 리플렉터가 들어오는 에너지를 리시버에 집중시키기 위해 사용되면 리시버의 그림자가 리플렉터의 일부인 포물체의 정점에 떨어지기 때문에 리플렉터의 일부가 낭비된다.이는 정점과 대칭축에서 오프셋되는 포물체의 세그먼트에서 반사체를 만들면 피할 수 있다.예를 들어 위의 그림에서 반사체는 P점과13 P점 사이의 포물체의 일부일 수 있다.리시버는 여전히 포물선의 초점에 위치하지만 반사체에 그림자를 드리우지는 않습니다.전체 반사기는 에너지를 받고, 그 에너지가 수신기에 집중됩니다.예를 들어 위성-TV 수신 접시 및 일부 천체 망원경(예: 그린 뱅크 망원경, 제임스 웹 우주 망원경)에서 자주 이루어진다.
태양로 및 기타 중요하지 않은 용도에 사용할 수 있는 정확한 축외 반사기는 용융 유리 용기가 회전 축에서 오프셋되는 회전로를 사용하면 매우 간단하게 만들 수 있습니다.덜 정확한 것은 위성 접시에 적합한 형태를 컴퓨터로 디자인한 후 판금으로 여러 개의 접시를 찍어낸다.
중위도에서 정지 TV위성으로 향하는 궤도반사기는 동축반사기보다 더 가파르다.그 결과 접시를 담는 팔이 짧아지고 접시에 눈이 쌓이지 않게 됩니다.
역사
포물선 반사체의 원리는 수학자 디오클레스가 그의 저서 불타는 거울에서 묘사하고 평행광선이 한 [4]점에 초점을 맞춘다는 것을 증명한 고전 고대부터 알려져 왔다.기원전 3세기에 아르키메데스는 정수적 [5]균형에 대한 그의 연구의 일환으로 포물체를 연구했고,[6] 그가 시라쿠사 공성전에서 로마 함대를 불태우기 위해 반사체를 사용했다고 주장되어 왔다.그러나 이 주장은 기원후 2세기 이전의 자료에는 나타나지 않고 디오클레스는 그의 [7]저서에 그것을 언급하지 않기 때문에 이는 사실이 아닌 것으로 보인다.포물선 거울은 또한 [8]10세기에 물리학자 이븐 살에 의해 연구되었다.제임스 그레고리(James Gregory)는 1663년 저서 옵티카 프로모타(1663)에서 포물선 모양의 거울이 달린 반사 망원경은 굴절 망원경에서 볼 수 있는 색 수차뿐만 아니라 구면 수차를 교정할 것이라고 지적했다.그가 고안한 디자인은 "그레고리안 망원경"이라는 이름을 가지고 있지만, 그레고리는 자신의 고백에 따르면 실용적인 기술이 없었고 [9]실제로 그것을 만들 수 있는 안경사를 찾을 수 없었다.아이작 뉴턴은 포물선 거울의 특성에 대해 알고 있었지만 그의 뉴턴식 망원경 거울의 구형을 건축을 [10]단순화하기 위해 선택했습니다.등대는 또한 19세기에 보다 효율적인 프레넬 렌즈로 대체되기 전에 랜턴에서 나오는 빛의 점을 빔으로 콜리메이트하기 위해 포물선 거울을 사용하기도 했다.1888년, 독일의 물리학자인 하인리히 헤르츠는 세계 최초의 포물선 반사 [11]안테나를 만들었다.
적용들
포물선 반사기의 가장 일반적인 현대적인 적용 분야는 위성 접시이며, 반사 망원경, 전파 망원경, 포물선 마이크, 태양열 조리기, 그리고 스포트라이트, 자동차 전조등, PAR 램프, LED [13]하우징과 같은 많은 조명 장치들을 포함한다.
올림픽 성화는 전통적으로 그리스 올림피아에서 햇빛을 집중시키는 포물선 반사경을 이용해 불을 붙인 뒤 올림픽 개최지로 옮겨진다.포물선 거울은 유리를 태우는 많은 모양 중 하나이다.
포물선 반사경은 착시현상을 만드는 데 널리 사용된다.이 거울은 두 개의 마주보는 포물선 거울로 구성되어 있으며 상단 거울 중앙에 구멍이 있습니다.아래쪽 미러에 물체를 배치하면 미러가 실제 이미지를 생성합니다.이것은 개구부에 표시되는 원본과 거의 동일한 복사본입니다.화질은 광섬유의 정밀도에 따라 달라집니다.그러한 환상은 100만분의 1인치까지 허용된다.
위쪽으로 향하는 포물선 반사체는 수은과 같은 반사 액체를 수직 축을 중심으로 회전시킴으로써 형성될 수 있다.이것은 액체 거울 망원경을 가능하게 한다.회전로에서도 동일한 기술이 사용되어 고체 반사체를 만듭니다.
또한 포물선 리플렉터는 무선 신호 강도를 높이기 위한 일반적인 대안입니다.단순한 것을 사용하더라도 사용자는 3dB 이상의 [14][15]이득을 보고했습니다.
「 」를 참조해 주세요.
각주
- ^ 자연 로그의 밑수인 "e"의 값에 대한 이 숫자의 근접성은 우연의 일치일 뿐이지만 유용한 니모닉이 됩니다.
레퍼런스
- ^ Fitzpatrick, Richard (2007-07-14). "Spherical Mirrors". Farside.ph.utexas.edu. Retrieved 2012-11-08.
- ^ "Servicing Mission 1". NASA. Archived from the original on April 20, 2008. Retrieved April 26, 2008.
- ^ Administrator. "The Scheffler-Reflector". www.solare-bruecke.org.
- ^ 162-164페이지, 페르가의 코니카의 아폴로니어스: 텍스트, 컨텍스트, 서브텍스트, 미카엘 N.프라이드 앤 사베타이 은구루, Bril, 2001, ISBN 90-04-11977-9.
- ^ 73-74페이지, 잊혀진 혁명: 어떻게 기원전 300년에 과학이 탄생했고 왜 과학이 다시 태어나야 했는지, Lucio Russo, Birkhauser, 2004, ISBN 3-540-20068-1.
- ^ "Archimedes' Weapon". Time Magazine. November 26, 1973. Archived from the original on October 12, 2007. Retrieved 2007-08-12.
- ^ 72페이지, 고대 불타는 거울의 기하학, 윌버 크노르, Isis 74 #1(1983년 3월), 53-73, doi:10.1086/353176.
- ^ 465, 468, 469페이지, 아나클라스틱의 선구자:거울과 렌즈를 태우는 이븐 살, 로쉬디 라셰드, 이시스, 81, 3위(1990년 9월), 페이지 464-491, doi:10.1086/355456.
- ^ Chambers, Robert (1875). A biographical dictionary of eminent Scotsmen. Oxford University. p. 175.
- ^ McLean, Ian S (2008-07-29). Electronic Imaging in Astronomy: Detectors and Instrumentation. Google Books. ISBN 9783540765820. Retrieved 2012-11-08.
- ^ "Prehistory of Radio Astronomy". www.nrao.edu.
- ^ "ALMA Doubles its Power in New Phase of More Advanced Observations". ESO Announcement. Retrieved 11 January 2013.
- ^ Fitzpatrick, Richard (2007-07-14). "Spherical Mirrors". Farside.ph.utexas.edu. Retrieved 2012-11-08.
- ^ "Parabolic Reflector Free WiFi Booster". Do-It-Yourself Wireless Antennas Update and Wi-Fi Resource Center WiFi Wireless Q & A. Binarywolf.com. 2009-08-26. Archived from the original on 2019-06-09. Retrieved 2012-11-08.
- ^ "Slideshow: Wi-Fi Shootout in the Desert". Wired. 2004-08-03. Retrieved 2012-11-08.
외부 링크
- 포물선 반사체의 Java 시연
- 포물선 리플렉터 안테나 www.antenna-theory.com
- QED에 의한 포물선 미러 시연 애니메이션
- 평면 세그먼트를 사용하여 큰 포물면 반사체 만들기




 초점거리, D {\
초점거리, D {\
 접시 깊이(V의 대칭축에 따른 길이)로 대응한다.ertex) 및
접시 깊이(V의 대칭축에 따른 길이)로 대응한다.ertex) 및 





 지정됩니다.이는
지정됩니다.이는

 (\displaystyle
(\displaystyle