광학적 수차
Optical aberration| 광학적 수차 |
|---|
광학에서 수차는 렌즈와 같은 광학계의 특성으로,[1] 빛이 한 점에 집중하기 보다는 공간의 특정 영역에 분산되도록 합니다.수차는 렌즈에 의해 형성되는 화상을 흐리게 하거나 왜곡시키는 원인이 되며, 수차의 종류에 따라 왜곡의 성질도 달라집니다.수차는 근축광학 [2]예측에서 광학계 성능의 이탈로 정의할 수 있다.영상촬영시스템에서는 사물의 한 지점으로부터의 빛이 시스템을 투과한 후 단일 지점으로 수렴되지 않을 때(또는 발산되지 않을 때) 발생합니다.수차는 단순한 근축 이론이 빛에 대한 광학계의 영향을 완전히 정확한 모델이 아니라 광학 [3]요소의 결함 때문에 발생합니다.
수차를 가진 영상 형성 광학 시스템은 선명하지 않은 영상을 생성합니다.광학기기 제조업체들은 수차를 보정하기 위해 광학계를 교정할 필요가 있다.
수차는 기하학적 광학 기술로 분석할 수 있다.반사, 굴절, 가성학에 관한 논문은 반사광과 굴절광의 일반적인 특징을 논한다.
개요
이상적인 렌즈를 사용하면 물체의 특정 지점에서 나오는 빛이 렌즈를 통과하여 이미지 평면(또는 일반적으로 이미지 표면)의 한 지점에서 모입니다.그러나 실제 렌즈는 완벽하게 만들어졌음에도 불구하고 빛을 정확히 한 점에 집중시키지 않는다.이상화된 렌즈 성능으로부터의 이러한 편차를 렌즈의 수차라고 합니다.
수차는 단색과 색색의 두 종류로 나뉜다.단색수차는 렌즈나 거울의 형상에 의해 발생하며 빛이 반사될 때와 굴절될 때 모두 발생합니다.단색광을 사용해도 나타나는 이름이라 할 수 있습니다.
색수차는 파장에 따른 렌즈의 굴절률의 변화인 분산에 의해 발생합니다.분산으로 인해, 다른 파장의 빛이 다른 지점에 집중됩니다.단색광을 사용하면 색수차가 나타나지 않습니다.
단색 수차
가장 일반적인 단색 이상은 다음과 같습니다.
디포커스는 광학 수차 중 기술적으로 가장 낮은 차수이지만 렌즈(또는 이미지 평면)를 움직여 이미지 평면을 렌즈의 광학 초점으로 가져옴으로써 보정할 수 있기 때문에 일반적으로 렌즈 수차로 간주되지 않습니다.
이러한 수차 외에도 피스톤과 틸트는 초점의 위치를 이동하는 효과입니다.피스톤과 틸트는 진정한 광학 이상이 아닙니다. 그렇지 않으면 완벽한 파면이 피스톤과 틸트에 의해 변경되어도 수차가 없는 완벽한 이미지를 형성하며, 다른 위치로만 이동하기 때문입니다.
색수차
색수차는 서로 다른 파장이 같은 지점에 집중되지 않을 때 발생합니다.색수차의 유형은 다음과 같습니다.
- 축방향(또는 "종방향") 색수차
- 가로(또는 "횡") 색수차
단색 수차 이론
고전광학 [4]이론의 완벽한 광학계에서는 어떤 물체점으로부터 진행되는 광선이 화상점에 집적되어 물체공간이 화상공간에서 재생된다.초점 거리와 초점 평면으로 명명된 가우스 [5][6]때문에 간단한 보조 용어의 도입은 모든 시스템에 대한 물체의 이미지를 결정할 수 있게 한다.그러나 가우스 이론은 광학 축(시스템의 대칭 축)을 가진 모든 광선에 의해 만들어진 각도가 무한히 작을 때에만 진실이다. 즉, 극소수 물체, 이미지 및 렌즈를 가진 경우, 실제로 이러한 조건은 실현되지 않을 수 있으며, 보정되지 않은 시스템에 의해 투영된 이미지는 일반적으로, 잘못 정의되고 정의되어 있다.개구부 또는 시야가 특정 [6]한계를 초과할 경우 10이 흐려집니다.
제임스 클러크 Maxwell[7]과 ErnstAbbe[8]의 수사는 광학 시스템이 이러한 복사물, 즉 상대적 위치와 이미지의 크기의 속성이 아니다 특별한 성질을 가지지만, 이미지의 우주의 모든 지점의 재생산의 그 상상(아베당)의 필요한 결과,indep 것으로 나타났다.endent재생산이 이루어지는 방식에 대해 설명합니다.그러나 이 저자들은 어떤 광학계도 이러한 가정들을 정당화할 수 없다는 것을 보여주었다. 왜냐하면 그것들은 반사와 굴절의 기본 법칙과 모순되기 때문이다.결과적으로, 가우스 이론은 현실을 근사하는 편리한 방법을 제공할 뿐이다; 현실 광학 시스템은 이 도달할 수 없는 이상에 미치지 못한다.현재 달성할 수 있는 것은 단일 평면을 다른 평면에 투영하는 것 뿐이지만, 이 경우에도 항상 이상 현상이 발생하고 이러한 현상이 완전히 [6]수정될 가능성은 거의 없습니다.
축점 수차(제한된 의미의 구면 수차)
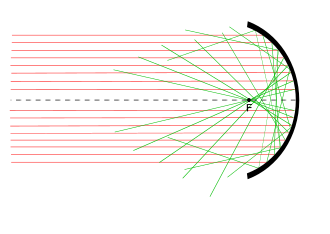
S(그림1)를 임의의 광학계라고 하면, 축점 O로부터 각도 u1아래로 흐르는 광선은 축점 O'1에, 각도 u2아래의 광선은 축점 O'2에 집결한다.집합 구면 또는 얇은 양의 렌즈를 통해 굴절이 있는 경우 각도 u2가 u1보다 크면 O'2는 O'1 앞에 있고(보정 중), 반대로 분산 표면 또는 렌즈와 함께(오버보정 중) O'2는 O'1 앞에 있습니다.첫 번째 케이스에서는 가성 부호가 > (보다 큼); 두 번째 < (보다 작음)과 비슷합니다.각도 u1이 매우 작을 경우, O'1은 가우스 화상, O'1 O'2는 세로 수차, O'1R은 개구 u2를 가진 연필의 가로 수차이다.각도 u2의 연필이 투과된 모든 연필의 최대 수차의 경우 O'1의 축에 수직인 평면에는 O'1R 반지름의 혼동의 원형 원반이 있고 O'2의 평행 평면에는 O'2R 반지름의 또 다른 원반이 있으며, 이들 사이에 [6]혼동이 최소인 원반이 있다.
O의 재생에 관여하는 연필의 가장 큰 개구부, 즉 각도 u는 일반적으로 렌즈의 가장자리 또는 시스템의 렌즈 앞 또는 뒤에 위치한 얇은 판의 구멍에 의해 결정된다.이 구멍을 스톱 또는 다이어프램이라고 합니다.Abbe는 구멍과 렌즈의 한계 여백 모두에 대해 조리개 스톱이라는 용어를 사용했습니다.조리개 스톱과 물체 O 사이에 위치한 시스템의 구성 요소 S1은 입구 동공 Abbe로 불리는 다이어프램의 이미지를 투영합니다. 출구 동공은 조리개 스톱 뒤에 위치한 구성 요소 S2에 의해 형성된 이미지입니다.O에서 방출되어 조리개를 통과하는 모든 광선은 조리개 정지 이미지이므로 입구 및 출구 동공을 통과합니다.O에서 나오는 연필의 최대 구멍은 현시점에서의 입구 동공에 의해 세팅된 각도 u이기 때문에 수차의 크기는 입구 동공의 위치와 직경에 의해 결정된다.시스템이 완전히 조리개 스톱 뒤에 있는 경우에는 입구 동공(프론트 스톱)이고, 완전히 전면인 경우에는 출구 동공(백 스톱)[6]입니다.
대상점이 무한히 먼 경우 시스템의 첫 번째 구성원에 의해 수신되는 모든 광선은 평행하며, 시스템을 횡단한 후 교차하는 광선은 수직 입사 높이, 즉 축으로부터의 거리에 따라 변화한다.이 거리는 앞의 고려사항에서 각도 u를 대체하며, 개구부, 즉 입구 동공의 반지름이 최대값이다.[6]
요소의 수차, 즉 축과 직각으로 가장 작은 물체
O에서 방출되는 광선(그림 1)이 동시에 발생하는 경우, 평면의 일부가 매우 작더라도 O에서 축에 수직인 평면의 일부에 있는 점도 동시에 발생하는 것은 아니다.렌즈의 직경이 증가함에 따라(즉, 조리개가 증가함에 따라), 인접한 점 N이 재현되지만 ON에 버금가는 크기의 수차가 수반됩니다.Abe에 따르면 사인 조건인 sin u'1/sin u1=sin u'2/sin u2가 점 O를 재생하는 모든 광선에 유지된다면 이러한 수차를 피할 수 있다.대상점 O가 무한히 멀면 u1과 u2를 입사 수직 높이인 h1과 h2로 치환하고 사인 조건은 sin u'1/h1=sin u'2/h2가 된다.이 조건을 충족하고 구면 수차가 없는 시스템을 평면도(그리스어 a-, privative, plann, warging)라고 한다.이 단어는 로버트 블레어가 뛰어난 무채색주의를 특징짓기 위해 처음 사용되었고, 그 후 많은 작가들에 의해 구면 이상으로부터의 자유를 나타내기 위해 사용되었다.[6]
수차는 렌즈의 중심으로부터의 광선의 거리에 따라 증가하기 때문에 렌즈 직경이 증가할수록(또는 이에 따라 조리개 직경에 따라), 따라서 조리개를 감소시킴으로써 화상 평면에 도달하는 빛의 양을 감소시키는 비용으로 최소화할 수 있다.
좁은 연필을 사용한 가로 방향 물체 점(축 밖의 점)의 수차 - 난시
축으로부터 유한한 거리에 있는 점 O(또는 무한히 먼 물체와 함께, 시스템에서 유한한 각도를 기울이는 점)는, 일반적으로, 이 점으로부터 발원해 시스템을 횡단하는 광선의 연필이 조리개를 줄임으로써 무한히 좁아지는 경우에서도, 선명하게 재현되지 않는다.이 연필은 광선으로 구성되어 있다.그 물체는 이제 무한히 작은 입구 동공을 통과할 수 있다.연필이 굴절 또는 반사 표면에 직각으로 닿지 않는 것으로 보여지므로 난시(Gr. a-, privative, stigmia, point)이다.입구 동공을 통과하는 중심 광선을 연필 또는 주 광선의 축으로 명명하면, 연필 광선이 한 점이 아닌 두 개의 초점 선으로 교차한다. 이 중 하나는 주 광선과 직각을 이루는 것으로 가정할 수 있다. 즉, 시스템의 축을 포함하는 평면에 있다.첫 번째 주요 섹션 또는 주변 섹션과 그에 직각인 다른 섹션, 즉 두 번째 주요 섹션 또는 시상 섹션.따라서 예를 들어 포커싱 스크린과 같이 시스템 뒤의 단일 가로채기 평면에서는 대상점의 이미지를 수신할 수 없습니다.한편, 2개의 평면에서는 각각 O'와 O'가 개별적으로 형성되며(인접 평면에서는 타원형이 형성됨), O'와 O' 사이의 평면에서는 혼동이 가장 적은 원이 형성됩니다.난시차이라고 불리는 간격 O'O"는 일반적으로 시스템의 축과 함께 주선 OP에 의해 만들어진 각도 W에 따라 증가한다(예: 시야).두 개의 난시상 표면은 하나의 물체 평면에 대응하고 있으며, 이것들은 축점에 접촉하고 있으며, 한쪽은 제1종의 초점, 다른 한쪽은 제2종의 초점 위에 놓여 있다.두 난시 표면이 일치하는 시스템을 문합계 또는 고정계라고 [6]한다.
아이작 뉴턴 경은 아마도 난시의 발견자였을 것이다; 난시 이미지 선의 위치는 토마스 [9]영에 의해 결정되었고, 그 이론은 올바 걸스트랜드에 [10][11][6]의해 개발되었다.P의 참고 문헌 목록.Culmann은 Optischen Instrumenten에 [12][6]있는 Moritz von Rohr의 Die Bilderzeugung에 나온다.
넓은 연필을 사용한 가로 방향 물체 점의 수차 - 혼수 상태
멈춤을 더 넓게 열면 축 점에 대해 이미 논의한 것과 유사한 편차가 횡방향 점에 대해 발생하지만, 이 경우에는 훨씬 더 복잡하다.자오선 부분의 광선의 코스는 연필의 주요 광선과 더 이상 대칭이 아닙니다; 그리고 가로채는 평면에는 광점 대신, 한 점에 대해 대칭적이지 않고, 종종 혜성의 꼬리가 축을 향하거나 축에서 멀리 떨어져 있는 것과 유사합니다.이 모양에서 이름을 따왔다.이전에는 유일하게 고려되었던 이 자오선연필의 비대칭 형태는 좁은 의미에서 혼수 상태일 뿐이며, 다른 혼수 오류는 Arthur König와 Moritz von Rohr에 [12]의해, 그리고 나중에는 Allvar Gulstrand에 [11][6]의해 치료되었다.
이미지 필드의 곡률
상기의 에러가 해소되면, 2개의 난시 표면이 결합해, 넓은 조리개로 선명한 화상을 얻을 수 있습니다.특히, 사진 촬영등의 평면면에 화상을 수신하는 경우는, 화상 표면의 곡률을 보정할 필요가 있습니다.대부분의 경우 표면은 [6]시스템을 향해 오목하게 되어 있습니다.
이미지 왜곡
화상이 선명해도 이상적인 핀홀 투영에 비해 왜곡될 수 있다.핀홀 투영에서 물체의 배율은 광축을 따라 카메라와의 거리에 반비례하므로 평평한 표면을 직접 가리키는 카메라가 그 평평한 표면을 재현한다.왜곡은 이미지를 균일하지 않게 늘리는 것으로 생각할 수도 있고, 필드 전체에 걸친 배율의 변동으로 간주할 수도 있습니다.「왜곡」에는, 화상의 임의의 변형이 포함되는 경우가 있습니다만, 종래의 촬상 광학에 의해서 발생하는 가장 현저한 왜곡 모드는, 화상의 중심이 주변보다 확대되는 「배럴 왜곡」입니다(그림 3 a).둘레가 중심보다 확대되는 역방향은 "핀쿠션 왜곡"이라고 합니다(그림 3b).이 효과는 렌즈 왜곡 또는 이미지 왜곡이라고 불리며 이를 보정하는 알고리즘이 있습니다.
왜곡이 없는 시스템을 직교(Orthoscopein to look) 또는 직선(직선)이라고 합니다.
이 수차는 재현의 선명도와는 상당히 다르다.즉, 선명하지 않은 재현에서는 그림에서 물체의 일부만 인식할 수 있는 경우 왜곡에 대한 문제가 발생한다.선명하지 않은 화상에서 빛의 패치가 대상점에 대응하고 있는 경우, 패치의 무게중심을 화상점, 예를 들어 포커스 스크린이 정지부 중앙을 통과하는 광선과 교차하는 점으로 간주해도 된다.조리개가 작아졌을 때 포커싱 스크린의 좋지 않은 이미지가 정지해 있는 경우, 이러한 가정은 정당화됩니다.실제로, 이것은 일반적으로 발생합니다.아베가 (가우스 이론의 주 광선과 혼동하지 말 것) 주 광선으로 명명한 이 광선은 첫 번째 굴절 전에는 입구 동공의 중심을 통과하고 마지막 굴절 후에는 출구 동공의 중심을 통과합니다.따라서 도면 정확도는 주 광선에 의해서만 결정되며, 영상 필드의 선명도 또는 곡률과는 무관합니다.그림 4를 참조하여 O'Q'/OQ = a' tan waa tan w = 1/N이며, 여기서 N은 이미지의 스케일 또는 확대입니다.N이 w의 모든 값에 대해 일정하려면 a' tan w'/a tan w도 일정해야 한다.비 a isa가 충분히 일정할 경우, 위의 관계는 Airy의 조건, 즉 tan w w tan w = 상수까지 감소한다.이 단순한 관계(Camb 참조).Phil. Trans., 1830, 3, 페이지 1)은 다이어프램에 대해 대칭이거나(간단히 이름 붙여진 대칭 또는 전체대칭 목적), 또는 크기 비율에 따라 다이어프램에서 배치되어 동일한 곡률을 나타내는 2개의 유사하지만 다른 구성 요소로 구성된 모든 시스템에서 충족된다(대칭 Obj).외부음); 이러한 시스템에서 황갈색 w' / 황갈색 w [6]= 1.
R. H. Bow(영국)는 이 관계가 유지되기 위해 필요한 a'/a의 항상성을 지적했다.일기장Photog., 1861) 및 Thomas Sutton(Photographic Notes, 1862)은 O에 의해 처리되었습니다.루머와 M. von Rohr(Zeit. f.Instrumentenk., 1897, 17, 1898, 18, 페이지 4).구면 수차 없이 입구 및 출구 동공의 중심에서 조리개 정지부의 중간을 재현해야 합니다.M. von Rohr는 에어리 조건과 보우-수튼 조건을 모두 만족시키지 못하는 시스템의 경우, a' cos w/a tan w는 물체의 한 거리 동안 일정할 것이라는 것을 보여주었다.이 결합된 조건은 척도 1을 사용하여 재현하는 홀대칭 목표에 의해 정확하게 충족되며, 재현 척도가 두 [6]구성 요소의 크기 비율과 동일한 경우 반대칭에 의해 충족된다.
제르니크 수차 모형
수차와 관련된 원형 파면 프로파일은 Zernike 다항식을 사용하여 수학적으로 모델링할 수 있다.1930년대에 프리츠 제르니케에 의해 개발된 제르니케의 다항식은 단위 반지름의 원에 걸쳐 직교한다.복잡한 수차 파면 프로파일은 개별적으로 다른 유형의 수차를 나타내는 일련의 적합계수를 산출하기 위해 Zernike 다항식으로 곡선 적합시킬 수 있다.이러한 Zernike 계수는 선형적으로 독립적이므로 전체 파면에 대한 개별 수차 기여도를 분리하여 별도로 정량화할 수 있다.
짝수 다항식과 홀수 다항식이 있다.짝수 Zernike 다항식은 다음과 같이 정의된다.
그리고 기묘한 제르니케 다항식이
여기서 m과 n은 n n m의 음이 아닌 정수이고, δ는 라디안 단위의 방위각, θ는 정규화된 반지름 거리입니다.방사 n { R_은 방위 의존성이 없으며 다음과 같이 정의된다.
{ style n -m (\ )= ) 。
처음 몇 개의 Zernike 다항식에 각각의 적합 계수를 곱하면 다음과 같다.[13]
| "피스톤", 파면의 평균값과 동일 | |
| "X-Tilt", 시상 방향의 전체 빔 편차 | |
| "Y-Tilt", 접선 방향의 전체 빔 편차 | |
| 초점이 맞지 않아 발생하는 포물선 파면인 "Defocus" | |
| X 또는 Y축을 따라 원통형인 "0° 난시" | |
| X축에서 ±45° 방향으로 원통형인 "45° 난시" | |
| "X-Coma", 수평 방향으로 영상 플레어링 | |
| "Y-Coma", 수직 방향으로 영상 플레어링 | |
| "3차 구면 수차" |
서 { }는 0≤{ displaystyle 0 \ 1의 정규화된 동공 반지름입니다. { \ \는 0 \ \ 의 동공 주위의 방위각입니다.는 파장의 파면 오차입니다.
사인 및 코사인(cosine)을 이용한 푸리에 합성에서와 같이 파면은 충분히 많은 수의 고차 Zernike 다항식으로 완벽하게 표현될 수 있다.그러나 대기 난류 또는 공기역학적 흐름장을 통한 전파에 의해 생성되는 것과 같이 매우 가파른 구배 또는 매우 높은 공간 주파수 구조를 가진 파면체는 파면의 미세한 공간 정의를 저역학적 필터하는 경향이 있는 Zernike 다항식에 의해 잘 모델링되지 않는다.이 경우 프랙탈 또는 특이값 분해와 같은 다른 피팅 방법을 사용하면 피팅 결과가 개선될 수 있습니다.
원 다항식은 Frits Zernike에 의해 회절의 영향을 고려한 이상 광학계의 점 이미지를 평가하기 위해 도입되었다.회절의 존재에서의 완벽한 점 이미지는 에어리에 의해 이미 1835년에 기술되었다.이상계(Zernike와 Nijboer)의 점 이미지에 대한 포괄적인 이론과 모델링에 도달하는 데 거의 100년이 걸렸다.Nijboer와 Zernike의 분석은 최적 초점 평면에 가까운 강도 분포를 설명한다.초점 영역의 훨씬 큰 부피에서 점 영상 진폭과 강도를 계산할 수 있는 확장 이론이 최근에 개발되었습니다(확장 Nijboer-Zernike 이론).이 점 이미지의 확장 Nijboer-Zernike 이론 또는 '점 확산 함수' 형성은 이미지 형성에 대한 일반적인 연구, 특히 높은 수치 개구부를 가진 시스템의 경우,[14] 그리고 그 이상에 대한 광학 시스템의 특성화에서 응용되었습니다.
이상에 대한 분석적 처리
몇 가지 재생 오류에 대한 이전의 검토는 확실한 수차를 별도로 논의하는 아베 이론에 속하며, 광학 기기의 구조에서 특정 오류를 제거하려고 하고, 경험에 의해 그 선택이 정당화되는 실질적인 요구에 매우 적합하다.그러나 수학적인 의미에서 이 선택은 임의적이다. 유한한 조리개를 가진 유한한 물체의 재현은 모든 확률에서 무한한 수의 수차를 수반한다.이 숫자는 물체와 개구부가 특정 차수의 무한히 작다고 가정할 경우에만 유한하다. 그리고 무한 소량의 각 순서, 즉 (유한 물체와 개구부에 대한) 현실에 대한 각 근사 정도와 함께, 특정한 수의 수차가 관련된다.이 연결은 무한 [6]급수를 통해 일반적으로 분석적으로 이상 현상을 다루는 이론에만 의해 제공됩니다.
대상점 O(그림5)에서 진행하는 광선을 좌표(θ, θ)로 정의할 수 있다.대상 평면 I의 이 점 O와 그 축에 대한 직각에서의 다른 2개의 좌표(x, y) 중 광선이 입구 동공에 교차하는 점, 즉 평면 II.마찬가지로 대응하는 화상선은 평면 I' 및 II'의 점(θ', θ', (x', y')에 의해 정의될 수 있다.이러한 4개의 평면 좌표계의 원점은 광학계의 축과 동일선상에 있을 수 있으며, 대응하는 축은 평행할 수 있습니다.4개의 좌표 θ', θ', x', y'는 각각 θ, θ, x, y의 함수이며, 시야 및 조리개가 무한히 작다고 가정하면 θ, θ, x, y는 무한소수의 차수가 같고, 결과적으로 θ', θ', θ', θ', x', y'를 θ의 승승차수로 확장함으로써 θ, θ, θ, θ, θ, x'의 y'의 y'의 함수이다.r 최저 전력광학계가 대칭인 경우 좌표계의 원점이 광학축 및 대응하는 축과 평행한 경우, θ, x, y'의 부호를 변경함으로써 값 θ', θ', x', y'도 마찬가지로 부호를 변경하되 산술값을 유지해야 한다는 것을 쉽게 알 수 있다. 즉, 직렬이 복원됨을 의미한다.d부터 표시되지 않은 변수의 [6]홀수 거듭제곱까지입니다.
생식의 성질은 점 O에서 다른 점 O'로 합쳐지는 광선에 의해 이루어지지만 일반적으로는 그렇지 않다. 일반적으로 θ, θ가 일정하지만 x, y가 변하면 θ', θ, θ'는 다르다.그것은 그 비행기 I과 II의 이미지에 축 근처의 평범한 가우시안 규칙에 의해서 형성된 것과 2등은 비행기들, 그리고 이들 규칙의 축에서 어느 정도의 거리에서 점 O의 연장선을 이루지는 못했지만, 현실에 해당하는 가우스 상점 O'0과 좌표, ξ'0 η'0에 의해 될 수 있const 것으로 가정할 수 있다.ructed. 쓰기 D'=ξ'-ξ'-''0과 D'=''-''-'',0 그렇다면 D'와 D'는 x, ,, x, y에 속하는 수차로, 위와 같은 이유로 직렬로 확장했을 때 홀수승만을 포함하는 크기 함수입니다.O를 통과하는 모든 광선의 수차에 따라 수차가 포함된 θ, θ, x, y의 최소 파워에 따라 빛의 패치가 평면 I'에 형성된다.J. Petzval(Bericht uber die Ergebnisse einiger dioptrischer Untersuchungen, Buda Pesth, 1843; Akad)에 의해 명명된 학위입니다. 시츠버, 빈, 1857년, 볼륨.xxiv. xxvi.) 화상의 숫자 순서는 홀수 거듭제곱일 뿐이며, m차 화상의 형성 조건은 D' 및 D' 계열에서 3차, 5차…(m-2)차 거듭제곱 계수가 사라져야 한다.가우스 이론의 이미지는 3차이고, 다음 문제는 5차 이미지를 얻거나 3차 거듭제곱 계수를 0으로 만드는 것입니다.이를 위해서는 5개의 방정식을 만족시켜야 합니다. 다시 말해, 3차에는 5개의 변경이 있으며, 이 [6]5차에는 5차 이미지가 생성됩니다.
광학계의 상수, 즉 반지름, 두께, 굴절률 및 렌즈 사이의 거리에 관한 이러한 계수의 식은 L에 의해 해결되었다. 세이델(아스트르)Nach., 1856, 페이지 289); 1840년에 J. Petzval은 출판되지 않은 유사한 계산으로부터 그의 초상화 목표를 구성했다. (M. von Rohr, Theorie und Geschichte des photographotischen Objectivs, Berlin, 1899 페이지 248 참조)그 이론은 S에 의해 상세하게 설명되었다.핀터스발더(Munchen).Acad. Abhandl., 1891, 17, 519페이지)는 또한 그의 작품에 대한 짧은 견해를 포함한 세이델의 사후 논문을 발표했다. Akad. Sitzber., 1898, 28, 395); A에 의해 더 간단한 형식이 주어졌다.Kerber(Beitrége zur Dioptrik, 라이프치히, 1895-6-7-8-9).A. Konig와 M. von Rohr(M. von Rohr, Die Bilderzeugung instrumenten, 페이지 317–323 참조)은 Kerber의 방법을 나타내며, Abebe 방법에 기초한 기하학적 고려에서 자이델 공식을 추론하고 분석 결과를 해석하였다(기하학적으로는 21pp).
수차는 렌즈의 반지름, &c 대신 시스템의 특성 함수 및 미분 계수를 통해 표현될 수 있다. 그러나 이러한 공식은 즉시 적용되지는 않지만 수차와 순서 사이의 관계를 제공한다.윌리엄 로완 해밀턴 경(영국 어소크).따라서 보고서, 1833, 페이지 360)는 3차 수차를 도출하였고, 이후 이 방법은 Cluck Maxwell(Proc)에 의해 추구되었다. 런던 수학. Soc., 1874–1875; (R. S. Heath와 L. A.의 논문도 참조).Herman), M.티센(베를린) 아카드, 시츠버, 1890, 35, 페이지 804), H. 브룬스(라이프치히). 수학, 물리 Ber., 1895, 21, 페이지 410) 그리고 특히 K에 의해 성공적으로.슈바르츠실트(괴팅겐). Akad. Abhandl., 1905, 4, No.1. 이렇게 해서 5차(9개)의 수차를 발견했고, 아마도 실용적인(Seidel) 공식의 가장 짧은 증거일 것이다.A. 걸스트랜드(초급 제공, 앤 d). Phys., 1905, 18, 페이지 941)는 표면의 [6]미분 기하학에 대한 그의 이상 이론을 확립했다.
3차 수차는 (1) 축 지점의 수차, (2) 축으로부터의 거리가 3차보다 작은 점의 수차, 즉 여기에서 사인 조건과 혼수 상태의 편차가 한 등급에 포함된다. (3) 난시, (4) 필드의 곡률, (5) [6]왜곡이다.
- (1) 제3의 축점 수차는 광학에 관한 모든 교과서에서 다루어진다.이것은 망원경 디자인에서 매우 중요하다.망원경에서 개구부는 보통 물체의 선형 직경으로 간주된다.물체의 입사 동공이나 시야를 기준으로 각도 측정으로 표현되는 현미경 구멍과는 다릅니다.망원경 설계의 고차 수차는 대부분 무시할 수 있다.현미경에 관해서는 무시할 수 없다.두께가 매우 작고 주어진 도수의 단일 렌즈의 경우, 수차는 반지름 r:r'의 비율에 따라 달라지며, 이 비율의 특정 값에 대한 최소값(하지만 절대 0이 아님)입니다. 굴절률(렌즈의 도수가 일정하게 유지됨)에 따라 반비례합니다.접촉하는 두 개 이상의 매우 얇은 렌즈의 총 수차는 개별 수차의 합이 0일 수 있습니다.이것은 렌즈가 같은 대수 부호를 가지고 있는 경우에도 가능합니다.n=1.5인 얇은 양극 렌즈 중 3차 구면 수차를 보정하기 위해 4개가 필요하다.그러나 이러한 시스템은 실질적으로 그다지 중요하지 않습니다.대부분의 경우, 두 개의 얇은 렌즈가 결합되어 있으며, 그 중 하나는 음의 렌즈로서 양의 수차(보정 부족, 비디오 수프라)가 매우 강하며, 첫 번째는 양의 렌즈여야 하며 두 번째는 음의 렌즈여야 합니다. 단, 도수는 다를 수 있으므로 렌즈의 바람직한 효과가 유지됩니다.일반적으로 하나의 고배율 렌즈보다 몇 가지 약한 굴절 효과를 확보할 수 있는 장점이 있습니다.1개, 마찬가지로 여러 개, 그리고 무한한 수의 접점 박렌즈로도 3차 수차 없이 2개 이하의 축점을 재현할 수 있다.한 축이 무한히 떨어져 있는 두 축 점에 대한 수차로부터의 자유는 허셜의 조건이라고 알려져 있습니다.렌즈의 두께와 거리는 고려하지 [6]않기 때문에 이 모든 규칙은 유효합니다.
- (2) 3차 혼수로부터 자유로워지는 조건은 망원경 목적에도 매우 중요하며, Fraunhofer's 상태라고도 한다. (4) 축, 혼수 및 난시에서의 수차를 제거한 후, 3차 혼수 및 난시에서의 필드 평탄도의 관계는 Petzval 방정식 S1/r(n'n'-n)에 의해 표현된다.굴절면의 아디우스, 인접 매체의 굴절률 n 및 n' 및 S는 모든 굴절면에 [6]대한 합계의 부호이다.
수차의 실질적인 제거
기존의 이미징 문제는 유한한 개구부를 통해 유한한 평면(물체)을 다른 평면(이미지)에 완벽하게 재현하는 것입니다.이러한 두 개 이상의 평면에 대해 완벽하게 그렇게 하는 것은 불가능하다(이는 1858년 맥스웰, 1895년 브룬스, 1926년 카라테오도리에 의해 증명되었다). 발터, A., J. 옵트. Soc. Am의 요약을 참조한다.A 6, 415~422(1989)그러나 단일 평면 쌍(예: 목표의 단일 초점 설정에 대한)의 경우, 원칙적으로 문제를 완벽하게 해결할 수 있다.이론적으로 완벽한 시스템의 예로는 루네부르크 렌즈와 맥스웰 어안이 있다.
실용적인 방법은 이 문제를 거의 각 종류의 계측기의 특수 목적에 적합한 정확도로 해결합니다.주어진 확대(수차를 고려해야 하는 경우)로 주어진 평면에서 주어진 물체를 재현하는 시스템을 찾는 문제는 근사 이론에 의해 처리될 수 있다. 그러나 대부분의 경우, 분석 난이도는 오래된 계산 방법에는 너무 컸지만 적용에 의해 개선될 수 있다.현대 컴퓨터 시스템의 이온.그러나 특수한 경우에는 해결 방법이 확보되었다(A 참조).M. von Rohr's Die Bilderzeugung, 373쪽, K.의 K.슈바르츠실트, 괴팅겐.Akad. Abhandl., 1905, 4, 2번과 3번)현시점에서는 생성자는 거의 항상 역법을 사용한다.즉, 특정, 종종 상당히 개인적인 경험으로부터 시스템을 구성하고 여러 광선의 경로를 삼각법으로 계산하여 시스템이 원하는 재생산을 제공하는지 여부를 테스트한다(예는 A에 제시되어 있다).Gleichen, Lehrbuch der Geometryshen Optik, 라이프치히 및 베를린, 1902).이미지의 오차가 충분히 작아질 때까지 반지름, 두께 및 거리가 지속적으로 변경됩니다.이 방법에 의해 특정 재생 오류만 조사되며, 특히 위에 명기된 개별 멤버 또는 모든 멤버를 조사한다.분석적 근사 이론은 일반적으로 [6]정확도가 충분하지 않기 때문에 잠정적으로 종종 사용된다.
구면수차와 사인조건으로부터의 편차를 조리개 전체에 걸쳐 작게 표현하기 위해 개구각 u*(무한 거리 물체: 입사높이가 h*)가 유한한 광선에 대하여 교차거리가 동일하고 인접한 축에 대하여 사인비가 동일(u* 또는 h*)하다.시스템에 사용되는 가장 큰 구멍 U 또는 H보다 작을 수 없습니다.)u*보다 작은 조리개 각도의 광선은 교차 거리 및 사인비가 동일하지 않습니다. 이러한 편차를 구역이라고 하며, 생성자는 이러한 편차를 최소화하려고 합니다.시야의 각도에 따른 오차도 마찬가지로 w: 난시, 시야의 곡률 및 왜곡을 제거하고 w*, 난시 구역, 시야의 곡률 및 왜곡을 w보다 작은 값에 추가한다.실제 안경사는 이러한 시스템을 다음과 같이 명명합니다. 즉, 조리개 u*(입사각 h*) 또는 시야각 w*에 대해 보정됩니다.구면수차 및 사인비의 변화를 조리개의 함수로 그래픽으로 나타내는 경우가 많아 축점의 화상평면의 2개의 난시상면의 편차가 [6]시야각의 함수로 표현되는 것과 같다.
따라서 실제 시스템의 최종 형태는 타협에 달려 있습니다. 즉, 조리개를 확대하면 사용 가능한 시야가 축소되고 그 반대도 마찬가지입니다.하지만 조리개가 클수록 해상도가 커집니다.다음은 [6]일반적인 것으로 간주할 수 있습니다.
- (1) 가장 큰 구멍, 필요한 보정은 축점과 사인 조건, 시야의 오차는 거의 무시된다. 예를 들어 고배율 현미경의 목적이다.
- (2) 광각 렌즈. 필요한 보정은 - 난시의 경우, 시야의 곡률 및 왜곡, 간극의 오차, 예 - 사진의 광각 목표 및 안구이다.
- 이러한 극단적인 예들 사이에 일반 렌즈가 있습니다. 이것은 조리개에 대해 더 많이 보정됩니다. 시야에 대해 더 많은 그룹에 대한 목표입니다.
- (3) Long Focus 렌즈는 시야가 좁기 때문에 축에 이상이 있는 것이 매우 중요합니다.따라서 구역은 가능한 작게 유지되며 디자인은 단순성을 강조해야 합니다.이 때문에, 이 렌즈는 해석 연산에 최적입니다.
색수차 또는 색수차
렌즈로 구성된 광학 시스템에서 이미지의 위치, 크기 및 오차는 사용된 유리의 굴절률에 따라 달라집니다(위의 렌즈(광학) 및 단색 수차 참조).굴절률은 빛의 색이나 파장에 따라 달라지기 때문에(분산 참조), 렌즈 시스템은 다소 다른 장소와 크기와 다른 수차로 서로 다른 색상의 이미지를 투사한다. 즉, 교차 거리, 확대 거리, 그리고 색상의 차이가 있다.단색 이상혼합된 빛(예: 흰색 빛)을 사용하는 경우 이러한 모든 이미지가 형성되고 색수차라고 하는 혼동을 일으킨다. 예를 들어 어두운 배경의 흰색 여백 대신 컬러 여백 또는 좁은 스펙트럼이 인식된다.이 오류가 없는 것을 무채색이라고 하며, 이렇게 보정된 광학계를 무채색이라고 합니다.시스템은 얇은 정렌즈와 같은 종류의 색오차를 보일 경우 색저보정을 하고, 그렇지 않을 경우 [6]색저보정을 한다고 한다.
애초에 단색수차가 무시된다면(즉, 가우스 이론이 받아들여진다면), 모든 생식은 초점면의 위치와 초점 거리의 크기에 의해 결정되거나, 또는 초점 거리가 보통 일어나는 것처럼, 세 개의 상수에 의해 동일하다면, 재생의 상수에 의해 결정된다.이러한 상수는 시스템의 데이터(렌즈의 반지름, 두께, 거리, 지수 등)에 의해 결정되므로 굴절률 및 결과적으로 색상에 [6]대한 의존성은 계산할 [16]수 있습니다.사용되는 각 종류의 유리에 대해 서로 다른 파장의 굴절률을 알아야 한다.이와 같이 재생의 어느 하나의 상수가 두 가지 다른 색상에 대해 동일하다는 조건이 유지된다. 즉, 이 상수는 무채색화된다.예를 들면, 공기중의 1개의 두꺼운 렌즈로, 초점 거리의 크기의 초점면의 위치를 무채색화할 수 있다.3가지 재생상수를 모두 무채색화하면 2가지 색상에서 물체의 모든 거리에 대한 가우스 화상이 같아져 안정된 무채색 [6]상태라고 할 수 있다.
실제로는 물체의 고정된 위치에 대한 색수차(예를 들어 교점 거리의 색수차)를 결정하고 각 성분이 각 굴절면에 [17][18][6]의한 양을 합한 합으로 표현하는 것이 더 유리하다.한 색상의 화상점을 포함한 평면에서 다른 색상은 혼동의 원반을 생성한다.이것은 구면 수차의 두 구역이 야기하는 혼돈과 유사하다.무한히 먼 물체의 경우 혼동의 색 디스크의 반경은 선형 개구부에 비례하며 초점 거리(초점, 축점의 단색 수차를 제공)와 독립적입니다. 그리고 이 디스크가 주어진 물체의 이미지가 증가하거나 초점 거리가 증가하면 덜 해롭기 때문에 다음과 같이 됩니다.이미지의 열화는 초점 거리에 대한 조리개 비율(상대 조리개)에 비례합니다.(이것은 무채색이 발견되기 전에 유행했던 거대한 초점 거리를 설명해준다.)[6]
예:
- (a) 초점거리와 초점의 거리가 같기 때문에 공기 중의 초점거리의 재생정수는 1개만 관측된다.한 색상의 굴절률이 n이고 색상의 굴절률이 n n+dn이고 초점 거리의 거듭제곱 또는 역수가 f이면 (1) (-) (\입니다. {dn { style dn은 분산,n { n[6]은 유리의 분산력이다
- 접촉에(b)2 얇은 렌즈:f1{\displaystyle f_{1}}와 f2{\displaystyle f_{2}}이 되는 권력에 굴절 지수의 1{\displaystyle n_{1}에 대해 렌즈에 해당하는}과 n2{\displaystyle n_{2}}와 틀 r1′{\displaystyle r'_{1}}, r1″{\displaystyle r"{1}.}, r2′{\displaystyle r'_{2}}, r2″{\displaystyle r"{2}}각각;f{\displaystyle f}는 총 에너지를 의미한다, df{\displaystyle의}, dn1{\displaystyle dn_{1}}, dn2{\displaystyle dn_{2}}f{\displaystyle f}의 변화, n1{\displays.Tyle n_{1}}, n2{\displaystyle n_{2}}색깔이.그리고 다음 관계:[6]을 가지고 있다.
- (2) 1 - 2 ( -) ( / - / )+ ( 2 -) ( - ) k1 + ( 2- ) ( \ f=_ { 1} - { }
- () d 1 + 2 ({ df_{22 비색도 df의 경우, (3)부터,
- (4) 1 / - 2 / 1({ k { / { } - _ { } / {} / = - n1 / ({ } / 2 - } } } } } ) 。집합 렌즈와 분산 렌즈로 구성되어 있습니다.따라서 (ff가 0이 되지 않도록 위해) 둘의 검정력이 달라야 하며 (4에 따라) 분산력도 달라야 한다.
뉴턴은 무채색주의에 의해 요구되는 서로 다른 분산력의 매체의 존재를 인지하지 못했다. 결과적으로 그는 굴절체 대신 큰 반사체를 만들었다.James Gregory와 Leonhard Oiler는 눈의 무채색성에 대한 잘못된 개념으로부터 올바른 견해에 도달했습니다; 이것은 1728년 Chester More Hall, 1754년 Clingenstierna 그리고 유명한 무채색 망원경을 만든 Dollond에 의해 결정되었습니다.([6]망원경 참조).
분산력이 약한 유리( 큰 v v는 크라운 글라스, 분산력이 큰 플린트 글라스로 불린다.무채색 집합렌즈 f의 구성에서는 (4)의 식에 따라 크라운 유리의 집합렌즈 I.와 플린트 유리의 분산렌즈 II.를 선택해야 하며, 후자는 약하지만 다른 한쪽은 더 큰 분산력으로 색보정한다.무채색 분산 렌즈의 경우 그 역치를 채택해야 한다.이는 현재 망원경 목적의 일반적인 유형으로, 4개의 반지름 값이 방정식 (2)와 (4)을 만족해야 한다.두 가지 다른 조건도 가정할 수 있습니다. 하나는 항상 축의 수차를 제거하는 것이고, 두 번째 조건은 허셜 또는 프라운호퍼 조건이며, 후자는 최상의 비디오 초프라, 단색 수차입니다.)그러나 실제로는 렌즈를 접촉시켜 두 번째 조건을 피하는 것이 더 유용합니다. 즉, 동일한 반지름입니다.P에 따르면.루돌프(에더의 자흐르브)photog., 1891, 5, 페이지 225; 1893, 7, 페이지 221)의 얇은 렌즈의 시멘트의 목표는 위에서와 같이 집합 렌즈가 더 작은 굴절률을 갖는 경우 축에서 구면 수차를 제거할 수 있게 한다. 반면에 집합 렌즈가 더 큰 굴절률을 갖는 경우, 그들은 난시와 필드의 곡률을 제거할 수 있게 한다.(이는 페츠발 방정식에서 나온 것이다. L. Seidel, Astr 참조).Nachr., 1856, 페이지 289).시멘트의 시스템이 양이면 렌즈가 양일수록 강력해야 하며, (4)에 따르면 더 큰 도수에 더 약한 분산력(더 큰 v이 있습니다. 즉, 크라운 글라스는 난시 및 평면 이미지에 대해 더 큰 굴절률을 가져야 합니다.그러나 이전의 모든 종류의 유리에서는 굴절률에 따라 분산력이 증가했습니다. 즉, n n이 할수록 v v가 감소했지만, E.Abe와 O에 의해 일부 제나 안경은 감소했습니다.쇼트는 높은 굴절률의 크라운 안경이었고, 이러한 크라운 안경에서 낮은 굴절률의 플린트 안경을 사용한 무채색 시스템은 새로운 무채색이라고 불리며, P에 의해 사용되었다.첫 번째 문합(사진 [6]목표)의 루돌프.
f {\ df를 소거하는 대신 특정 값을 할당하면 2개의 렌즈를 추가하여 원하는 색편차를 얻을 수 있습니다. 예를 들어 시스템의 다른 부분에 존재하는 1개의 렌즈를 제거할 수 있습니다.렌즈 I.와 II.가 시멘트가 되어 한 색에 대해 동일한 굴절률을 갖는 경우, 그 한 색에 대한 효과는 한 조각의 렌즈에 대한 효과입니다. 이러한 렌즈의 분해에 의해 구면 효과를 변경하지 않고 원하는 대로 색채 또는 무채색으로 만들 수 있습니다.그 색효과( d /f { df/ )가 같은 렌즈보다 크며, 2개의 유리가 분산되어 있는 것을 초색소라고 [6]한다.
D로 분리된 두 개의 얇은 렌즈({D})에서 무채색 조건은 1 + f {1} f_{2} f_{2}이다 v v {} =2}2} f_2} e} (같은 렌즈로 만들어진 )이다.(\[6] D}+2})/ 눈의 조건입니다
예를 들어 초점거리와 같은 재현정수가 두 가지 색상에 대해 동일할 경우 두 개의 다른 안경이 사용되면 다른 색상에 대해서도 동일하지 않습니다.예를 들어 2/ 1 ({}/이 스펙트럼 내에서 다르기 에 접촉하는 2개의 얇은 렌즈에 대한 무채색도 조건(4)은 스펙트럼의 한 부분에서만 충족된다.이 사실은 J. 프라운호퍼에 의해 처음 확인되었는데, 그는 태양 스펙트럼의 어두운 선으로 색을 정의했고, 두 개의 잔의 분산 비율이 빨간색에서 보라색까지 약 20%가 다르다는 것을 보여주었다(유리와 물의 변화는 약 50%).두가지 색, a와 b에 그러므로, fa=fb)f{\displaystyle f_{}=f_{b}=f}, 세번째 색, c에 초점 길이, 즉 만약 ca와 b사이에 놓여 있다, c<>f{\displaystyle f_{c}<, f}, 반대하는; 이러한 대수 결과는 사실은 적자로의 분산으로부터 얻어지는 것 f. 다르다그네거티브 플린트의 바이올렛을 향해 포지티브 크라운 글라스가 우세합니다.두 가지 색에 대해 무채색인 이러한 시스템의 색 오류는 2차 스펙트럼이라고 불리며, 1차 색 오류와 [6]같은 방식으로 조리개와 초점 거리에 의존합니다.
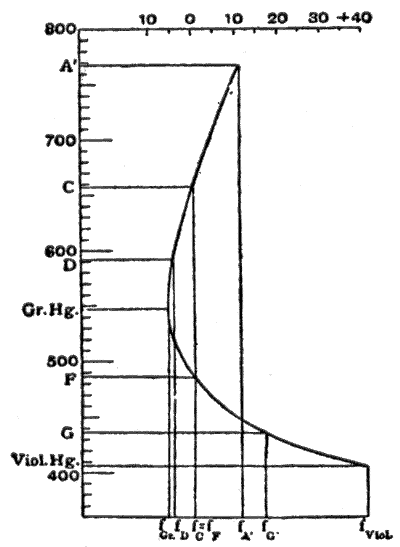
그림 6에서는 M. von Rohr의 Theory and Geschichte des photographitischen Objectivs에서 가져온 편광은 초점거리이며 파장은 규칙적이다.사용되는 Fraunhofer 행은 인접 [6]표에 나타나 있습니다.
| A' | C | D | 그린 Hg | F | G' | 바이올렛 Hg |
| 767.7 | 656.3 | 589.3 | 546.1 | 486.2 | 454.1 | 405.1 nm |
초점거리는 선 C와 F에 대해 동일합니다.550nm 부근에서 곡선에 대한 접선은 파장 축에 평행하며, 초점 거리는 적어도 매우 넓은 범위의 색에 걸쳐 변화하므로 이 부근에서는 색 합성이 가장 좋습니다.또한 스펙트럼의 이 영역은 인간의 눈에 가장 밝게 보이는 영역이며, 결과적으로 C {\} =F로 하여 얻은 스펙트럼의 이차 곡선은 G. G. Stokes 경(Proc)의 실험에 따른 것이다.Roy. Soc., 1878년, 시각 기구에 가장 적합(광학적 무채색증).마찬가지로 사진에 사용되는 시스템의 경우 색곡선의 정점을 플레이트의 최대 감도 위치에 배치해야 하며, 이는 일반적으로 G'로 추정되며, 이를 위해 F와 제비꽃 수은선이 일체화된다.이 기법은 천체 사진 촬영 목적(순수 무채색증)에 특별히 채택되었다.그러나 일반 사진에는 이러한 단점이 있습니다. 즉, 초점 화면의 이미지와 사진 감응판의 정확한 조절이 기록되지 않습니다. 천문학 사진에서는 이 차이가 일정하지만 다른 종류의 사진에서는 사물의 거리에 따라 달라집니다.이 때문에, 선 D와 G'는 통상의 촬영 목적을 위해서 일체가 되어 있다.광학 화상과 액티닉 화상은 색적으로는 열등하지만, 둘 다 같은 장소에 놓여 있다.따라서 최선의 보정은 F에 있다(이것은 액티닉 보정 또는 화학적 [6]초점으로부터의 자유라고 알려져 있다).
두 렌즈가 3가지 색상 a, b 및 c에 대해 동일한 초점 거리를 접촉하는 경우, 즉 b c= _ { b } = f _ { f _ { c } = f _ b=_ { 、 n - ( n - b ) \ ( { c _ { b )고용되어 있다.따라서 ac와 bc의 두 가지 색상 쌍에 대한 방정식 (4)을 고려합니다.최근까지 흡수도가 비례하는 안경은 알려져 있지 않았다; 다만 R이었다.블레어(트랜스).Edin. Soc., 1791, 3, 페이지 3) P. Barlow와 F.S. Archer는 유리벽 사이에 유체렌즈를 제작하여 어려움을 극복했다.프라운호퍼는 2차 스펙트럼을 줄이는 안경을 준비했지만, E.Abbe와 O가 제나 안경을 도입했을 때만 영구적인 성공을 보장했다.쇼트.비례분산을 가지지 않는 안경을 사용하는 경우, 2개의 렌즈에 의해, 또는 3개의 렌즈에 의해 제3색의 편차를 없앨 수 있다.3가지 색상을 결합하면 더 높은 차수의 무채색성이 도출됩니다. 아직 3차 스펙트럼이 남아 있지만 항상 [6]무시될 수 있습니다.
가우스 이론은 근사치일 뿐이며, 단색 또는 구면 수차는 여전히 발생하며, 이는 다른 색에 따라 다를 것이다. 그리고 만약 그것들이 한 색에 대해 보상된다면, 다른 색상의 이미지는 혼란스러운 것으로 판명될 것이다.가장 중요한 것은 다른 색상의 근축선이 적절한 유리 조합에 의해 결합된 후에도 여전히 영상을 방해할 수 있는 축점의 수차의 색차이다.일정한 파장에 대해 축점에 대해 집합 시스템을 보정하는 경우, 부성분인 플린트 글라스의 분산이 크기 때문에 짧은 파장에 대해서는 과잉 보정이 발생하고(이것은 부성분의 오차), 긴 파장에 대해서는 과소 보정이 발생합니다(크라운의 오차).유리렌즈(빨간색)를 나타냅니다.이 오류는 Jean Le Rond d'Alembert에 의해, 특히 C에 의해 처리되었습니다.F. 가우스이것은 조리개와 함께 빠르게 증가하고, 근축선의 2차 스펙트럼보다 중간 구멍에서 더 중요하다. 따라서 구면 수차는 두 가지 색상에 대해 제거되어야 하며, 이것이 불가능할 경우, 해당 기기에 가장 효과적인 특정 파장에 대해 제거되어야 한다(g).M. von Rohr, Theorie and Geschichte des photographyischen Objectivs)[6]에 이 오류의 알파벳 표현이 제시되어 있다.
선명하게 재현된 점 대신 표면 요소를 재현하기 위한 조건 - 사인 관계의 상수도 여러 색상에 대해 큰 구멍으로 충족되어야 합니다.E. Abebe는 축점의 오차로부터 현미경 목표를 계산하고 여러 색에 대한 사인 조건을 만족시키는 데 성공했습니다. 따라서 그의 정의에 따르면, 그가 아포크로매틱이라고 부르는 시스템들은 여러 색에 대해 무계획적이었습니다.그러나 개별 구역의 배율은 동일하지만 빨간색과 파란색은 동일하지 않으며 배율의 색차이가 있다.이것은 같은 양이지만 반대로 Abbe가 이러한 목적(안구 보정)에 사용한 안구에 의해 생성되어 전체 현미경의 이미지에서 사라집니다.최상의 망원경 목적과 3색 작업을 위한 사진 목적 또한 현미경 목적과 같은 보정 품질을 가지고 있지 않더라도 원색적이다.다른 재생산 오류의 색차이는 거의 실용적으로 [6]중요하지 않다.
「 」를 참조해 주세요.
레퍼런스
- ^ Kirkpatrick, Larry; Wheeler, Gerald (1992). Physics: A World View (2nd ed.). Philadelphia: Harcourt Brace College Publishers. p. 410. ISBN 0-03-000602-3.
- ^ Guenther, Robert (1990). Modern Optics. Cambridge: John Wiley & Sons Inc. p. 130. ISBN 0-471-60538-7.
- ^ "Comparison of Optical Aberrations". Edmund Optics. Archived from the original on December 6, 2011. Retrieved March 26, 2012.
- ^ 티센, M. (1890년) 베를린 아카드, 앉아서그리고 (1892) xxxv. 799; 베를린. 물리, Ges. Verh; 브룬스, H.(1895) 라이프치히. 수학, 물리 해밀턴 경의 특징적 기능(아일랜드 아카데미)에 의한 Ber., 215. 325.트랜스,광선계 이론, 1828 등).Czapski-Eppenstein, 페이지 155–161의 논문도 참조할 수 있다.
- ^ 가우스, 카를 프리드리히(1841), 괴팅겐 디옵트리스체 운터수춘겐.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao ap 앞의 문장 중 하나 이상에는 현재 퍼블릭 도메인에 있는 출판물의 텍스트가 포함되어 있습니다.
- ^ 맥스웰, 제임스 클락(1856) 필.Mag. 및 (1858) 쿼트. 일기장. 수학..
- ^ 에른스트 아베의 기하학 광학 연구는 원래 그의 대학 강의에서만 발표되었으며, 1893년 S. Czapski에 의해 처음 편집되었습니다.자세한 내용은 아래를 참조하십시오.
- ^ 영, 토마스(1807), 자연철학 강의 과정.
- ^ 걸스트랜드, 올바르(1890) 스칸드. 아아치 생리.; 및 (1901) Arch. f. 오브스, 53페이지, 2페이지, 185
- ^ a b Gullstrand, Allvar (1900). "Allgemeine Theorie der monochromat. Aberrationen, etc". Annalen der Physik. Upsala. 1905 (18): 941. Bibcode:1905AnP...323..941G. doi:10.1002/andp.19053231504.
- ^ a b von Rohr, Moritz (1904). Die bilderzeugung in optischen Instrumenten vom Standpunkte der geometrischen Optik. Berlin.
- ^ Schroeder, D. J. (2000). Astronomical optics (2nd ed.). San Diego: Academic Press. ISBN 978-0-08-049951-2. OCLC 162132153.
- ^ Born, Max; Wolf, Emil (1999-10-13). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. ISBN 978-0521642224.
- ^ "New Laser Improves VLT's Capabilities". ESO Announcement. Retrieved 22 February 2013.
- ^ 공식은 다음과 같습니다.
- ^ 참조
- ^ A. M. v. Rohr 소장품, Die Bilderzeugung, 340쪽
외부 링크
- 현미경의 목적: Molecular Expressions 웹사이트의 광학 수차 섹션, Michael W. Davidson, Mortimer Abramowitz, Olympus America Inc 및 Florida State University











 방위 의존성이 없으며 다음과 같이 정의된다.
방위 의존성이 없으며 다음과 같이 정의된다.













 0
0
 파장의 파면 오차입니다.
파장의 파면 오차입니다. 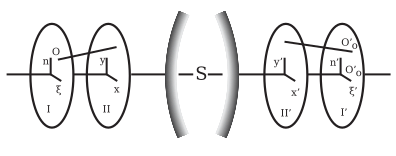












 소거하는 대신 특정 값을 할당하면 2개의 렌즈를 추가하여 원하는 색편차를 얻을 수 있습니다. 예를 들어 시스템의 다른 부분에 존재하는 1개의 렌즈를 제거할 수 있습니다.렌즈 I.와 II.가 시멘트가 되어 한 색에 대해 동일한 굴절률을 갖는 경우, 그 한 색에 대한 효과는 한 조각의 렌즈에 대한 효과입니다. 이러한 렌즈의 분해에 의해 구면 효과를 변경하지 않고 원하는 대로 색채 또는 무채색으로 만들 수 있습니다.그 색효과( d
소거하는 대신 특정 값을 할당하면 2개의 렌즈를 추가하여 원하는 색편차를 얻을 수 있습니다. 예를 들어 시스템의 다른 부분에 존재하는 1개의 렌즈를 제거할 수 있습니다.렌즈 I.와 II.가 시멘트가 되어 한 색에 대해 동일한 굴절률을 갖는 경우, 그 한 색에 대한 효과는 한 조각의 렌즈에 대한 효과입니다. 이러한 렌즈의 분해에 의해 구면 효과를 변경하지 않고 원하는 대로 색채 또는 무채색으로 만들 수 있습니다.그 색효과( d