보기와 말하기 순서

선은 시작점 23(빨간색), 1(파란색), 13(보라색), 312(녹색)로 구성된 look-and-say 시퀀스의 자릿수 증가를 보여준다. 이 선들(로그 수직 척도로 표현되는 경우)은 경사가 콘웨이의 상수와 일치하는 직선인 경향이 있다.

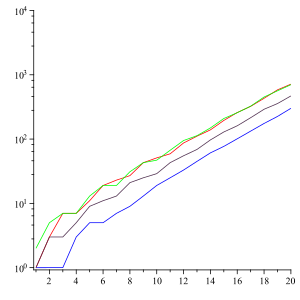
수학에서 look-and-say 순서는 다음과 같이 시작되는 정수의 순서다.

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ...(OEIS에서 시퀀스 A005150).

이전 멤버에서 시퀀스 멤버를 생성하려면 이전 멤버의 숫자를 읽고 동일한 숫자의 그룹에 있는 자릿수를 계산하십시오. 예를 들면 다음과 같다.

1은 "1" 또는 11로 읽힌다.
11은 "1초 2" 또는 21로 읽힌다.
21은 "하나 둘, 그 다음에 하나" 또는 1211로 읽힌다.
1211은 "하나의 1, 하나 둘, 그리고 두 개의 1s" 또는 111221로 읽힌다.
111221은 "3개의 1초, 2개의 2초, 1개의 1" 또는 312211로 읽힌다.

겉보기 순서는 존 콘웨이에 의해 소개되고 분석되었다.^[1]

look-and-say 시퀀스의 개념은 run-length 인코딩의 개념과 유사하다.

0에서 9까지의 숫자 d로 시작하는 경우 d는 시퀀스의 마지막 자릿수로 무한정 유지된다. 1 이외의 d의 경우 시퀀스는 다음과 같이 시작한다.

d, 1d, 111d, 311d, 13211d, 111312211d, 31131122211d, …

Ilan Vardi는 이 시퀀스를 d = 3, Conway 시퀀스(OEIS의 시퀀스 A006715). (d = 2는 OEIS: A006751 참조)^[2]로 불렀다.

기본 속성

복잡한 평면에 표시된 콘웨이 다항식의 뿌리. 콘웨이의 상수에는 그리스 문자 람다(λ田)가 표시되어 있다.

성장

순서가 무한히 커지다. 실제로 다른 정수 시드 번호로 시작하여 정의한 모든 변종도 22, 22, 22, 22, 22, … (OEIS에서 시퀀스 A010861)을 제외하고 무한히 성장할 것이다.^[3]

자릿수 존재 제한

시드 번호에 이러한 자릿수를 포함하거나 같은 자릿수의 3개 이상의 런이 없는 한, 1, 2, 3개 이외의 자릿수는 시퀀스에 나타나지 않는다.^[3]

우주적 붕괴

콘웨이의 우주론적 정리는 모든 시퀀스가 결국 "원자 요소"의 시퀀스로 분열되고 ("데이즈") 이것은 다시는 이웃과 상호작용하지 않는 유한한 부분이라고 주장한다. 숫자 1, 2, 3만 포함한 92개의 원소가 있다(92는 정확히 존슨 고형분의 수이고 정확히 비초우라늄 원소의 수이다). 존 콘웨이는 우라늄까지의 화학 원소의 이름을 따서 그 순서를 오디오 액티브라고 불렀다. 또한 각 자리에는 1, 2, 3개 외에 두 개의 "투명" 요소가 있다.^[3]^[4]

길이성장

그 용어는 결국 세대당 약 30%씩 길어졌다. 특히 L이_n 시퀀스 n번째 부재의 자릿수를 나타내는 경우, ${\frac {L_{n+1}}{L_{n}}}$ ${\frac {L_{n+1}}{L_{n}}}$ n + ${\frac {L_{n+1}}{L_{n}}}$ ${\frac {L_{n+1}}{L_{n}}}$ ${\frac {L_{n+1}}{L_{n}}}$ ${\$ }:{n+1}{{n+1 $}}$ 의 제한 값 $L_{n}}}}$ 이(가) 존재하며 ${\frac {L_{n+1}}{L_{n}}}$ 다음을 통해 제공됨

\lim _{n\to \inflt }{\frac {L_{n+1}:{n1}:{n\to \flt}{nL_{n}}=\lambda

여기서 λ = 1.303577269034... (OEIS에서 순서 A014715)는 71도의 대수적 수이다.^[3] 이 사실은 콘웨이에 의해 증명되었고, 상수 λ은 콘웨이의 상수로 알려져 있다. 또한 22개 이외의 다른 시드로 시작하는 시퀀스의 모든 변종에도 동일한 결과가 유지된다.

다항식 루트로서의 콘웨이 상수

콘웨이의 상수는 다음 다항식의 고유한 양의 실제 근이다: (OEIS의 순서 A137275).

{\displaystyle{\begin{정렬}&, \,\,\,\,\,\,\,x^{71}&,&&&-x^{69}&, &, -2x^{68}&, &, -x^{67}&, &, +2x^{66}&, &, +2x^{65}&, &, +x^{64}&, &, -x^{63}\\&, -x^{62}&, &, -x^{61}&, &, -x^{60}&, &, -x^{59}&, &, +2x^{58}&, &, +5x^{57}&, &, +3x^{56}&, &, -2x^{55}&, &, -10x^{54}\\&-3x^{53}&, &, -2x^{52}&, &, +6x^{51}&, &, +6x^{50}&, &, +x^{49}&, &, +9x^{48}&, &, -3x^{47}&, &, -7x^{46}&, &, -8x^{45}\\&, -8x^{44}&, &, +10x^{43}&, &, +6x^{42}&, &, +8x^{41}&,&-5x^{40}&&-12x^{39}&, &, +7x^{38}&, &, -7x^{37}&, &, +7x^{36}\\&, +x^{35}&, &, -3x^{34}&, &, +10x^{33}&, &, +x^{32}&, &, -6x^{31일}&, &, -2x^{30}&, &, -10x^{29}&, &, -3x^{28}&, &, +2x^{27}\\&, +9x^{26}&, &, -3x^{25}&, &, +14x^{24}&, &, -8x^{23}&,&&&-7x^{21}&,&+9x^{20}&a융점,&+3x^{19}&, &, -4x^{18}\\&, -10x^{17}&, &, -7x^{16}&, &, +12x^{15}&, &, +7x^{14}&, &, +2x^{13}&, &, -12x^{12}&, &, -4x^{11}&, &, -2x^{10}&,&+5x^{9}\\&&&+x^{7}}&-7x^{6}&+7x^{5}&-4x^{4}&+12x^{3}&-6x^{2}&+3x&-6x&-6\ed}}}}}}

콘웨이는 원문에서 x $x^{35}$ ${\$ 앞에 + 대신 이 다항식 글에 대해 부정확한 값을 주지만, 그의 글에 주어진 $λ$ 의 값은 정확하다 $x^{35}$ ^[5]

대중화

겉보기 순서는 암호학자 로버트 모리스의 뒤를 이어 모리스 번호 순서도 널리 알려져 있으며, 클리포드 스톨의 책 뻐꾸기 알에서 모리스에 대한 설명에서 "순서의 다음 숫자는 무엇인가?"라는 퍼즐은 때때로 뻐꾸기 알로 언급되기도 한다.^[6]^[7]

변형

look-and-say 시퀀스를 생성하는 데 사용되는 규칙에는 여러 가지 가능한 변형이 있다. 예를 들어, "pea pattern"을 형성하기 위해서는 전항을 읽고 연속 블록에서 발생하는 인스턴스뿐만 아니라 첫 번째 출현 순서로 나열된 각 자릿수의 모든 인스턴스(instance)를 계산한다. 따라서 종자 1을 시작으로 완자 패턴은 1, 11("1"), 21("2 "1"), 1211("1 2 및 1"), 3112("3 "1" 및 1"), 132112("1", 2 "1" 및 2"), 311322(" 3 "1" 및 2") 등이 진행된다. 이 버전의 완두 패턴은 결국 23322114와 32232114라는 두 용어로 주기를 형성한다.^[8]

다른 버전의 완두콩 패턴도 가능하다. 예를 들어, 숫자가 처음 나타날 때 숫자를 읽는 대신 오름차순으로 읽을 수 있다. 이 경우, 다음 21은 1112("하나 1, 하나 2"), 3112는 211213("2개의 1초, 하나 2, 하나 3")이 된다.

이러한 순서는 외관상 순서와 몇 가지 주목할 만한 방식으로 다르다. 특히, 콘웨이 시퀀스와는 달리, pea 패턴의 특정 항이 전항을 고유하게 정의하지는 않는다. 또한, 어떤 씨앗에 대해서도 완두 패턴은 한정된 길이의 항을 생성한다. 이 바운드는 일반적으로 2 * radix + 2자리를 초과하지 않으며, 변질된 긴 초기 씨앗("100개 등")의 경우 3 * radix 자릿수만 초과할 수 있다. 이러한 최대 경계 사례의 경우, 시퀀스의 개별 요소는 소수점 A0b1c2d3e4f5g6h7i8j9 형식을 취하며, 여기서 문자는 시퀀스의 선행 요소에서 숫자 카운트에 대한 자리 표시자입니다. 이 순서가 무한하고 길이가 한정되어 있다는 점에서 결국 비둘기구멍 원리로 인해 반복해야 한다. 결과적으로, 이러한 시퀀스는 결국 항상 주기적이다.

참고 항목

참조

^ Conway, John (January 1986). "The Weird and Wonderful Chemistry of Audioactive Decay". Eureka. 46: 5–16. Archived from the original on 2014-10-11.
^ 2011년 2월 4일 선에서 접속된 콘웨이 시퀀스, MathWorld.
^ ^a ^b ^c ^d Martin, Oscar (2006). "Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA" (PDF). American Mathematical Monthly. Mathematical association of America. 113 (4): 289–307. doi:10.2307/27641915. ISSN 0002-9890. JSTOR 27641915. Archived from the original (PDF) on 2006-12-24. Retrieved January 6, 2010.
^ Ekhad, S. B., Zeilberger, D.: Conway의 잃어버린 우주론적 정리 증명, 미국수학회의 전자 연구 발표, 1997년 8월 21일, Vol. 5, 페이지 78–82. 2011년 7월 4일 검색됨
^ Ilan Vardi, Mathematica의 컴퓨터 레크리에이션
^ 로버트 모리스 시퀀스
^ Morris 번호 순서에 대한 FAQ
^ "Ascending Pea Pattern generator". codegolf.stackexchange.com. Retrieved 2016-05-07.

외부 링크

콘웨이가 이 순서에 대해 말하고, 순서에 대해 이해하려면 몇 가지 설명이 필요하다고 말했어.
Rosetta Code에서 다양한 프로그래밍 언어로 구현
Weisstein, Eric W. "Look and Say Sequence". MathWorld.
Look and Say 시퀀스 생성기 p
OEIS 시퀀스 A014715(콘웨이 상수의 십진수 확장)
콘웨이 학위-71 다항식의 유래

[1] Conway, John (January 1986). "The Weird and Wonderful Chemistry of Audioactive Decay". Eureka. 46: 5–16. Archived from the original on 2014-10-11.

[2] 2011년 2월 4일 선에서 접속된 콘웨이 시퀀스, MathWorld.

[Martin2006-3] Martin, Oscar (2006). "Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA" (PDF). American Mathematical Monthly. Mathematical association of America. 113 (4): 289–307. doi:10.2307/27641915. ISSN 0002-9890. JSTOR 27641915. Archived from the original (PDF) on 2006-12-24. Retrieved January 6, 2010.

[4] Ekhad, S. B., Zeilberger, D.: Conway의 잃어버린 우주론적 정리 증명, 미국수학회의 전자 연구 발표, 1997년 8월 21일, Vol. 5, 페이지 78–82. 2011년 7월 4일 검색됨

[5] Ilan Vardi, Mathematica의 컴퓨터 레크리에이션

[6] 로버트 모리스 시퀀스

[7] Morris 번호 순서에 대한 FAQ

[8] "Ascending Pea Pattern generator". codegolf.stackexchange.com. Retrieved 2016-05-07.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Search