이산 전역 그리드

Discrete global grid
지오디
Azimutalprojektion-schief kl-cropped.png
기초
개념
기술
표준(이력)

이산 지구 그리드(DGG)는 지구 표면 전체를 덮고 있는 모자이크다. 수학적으로 그것은 공간 파티셔닝이다: 그것은 지구 표면의 파티션을 형성하는 비어있지 않은 지역들로 구성되어 있다.[1] 통상적인 그리드 모델링 전략에서는, 위치 계산을 단순화하기 위해, 각 지역을 점으로 나타내, 그리드를 지역 포인트 집합으로 추상화한다. 그리드의 각 지역 또는 지역 지점을 셀이라고 한다.

그리드의 각 셀이 재귀적 파티션에 따라 "진행적으로 더 미세한 해상도를 가진 이산형 글로벌 그리드의 시리즈"[2]가 생성되어 계층적 그리드를 형성하는 경우, 계층적 그리드(때로는 "글로벌 계층적 [3]테셀레이션" 또는 "DGG 시스템")로 명명된다.

이산 글로벌 그리드는 지리공간 데이터 구조 구축을 위한 기하학적 기준으로 사용된다. 각 셀은 데이터 객체 또는 값과 관련되거나, (위계층의 경우) 다른 셀과 관련될 수 있다. DGG는 벡터 및 래스터 위치 표현, 데이터 융합, 공간 데이터베이스 등 광범위한 지리공간 애플리케이션에서 사용하기 위해 제안되었다.[1]

가장 일반적인 그리드는 WGS84와 같은 표준 기준점을 사용하여 수평 위치 표현을 위한 것이다. 이러한 맥락에서, 지오코딩 표준화의 기초로서 특정 DGG를 사용하는 것도 일반적이다.

공간 지수의 맥락에서 DGG는 공간 인덱싱, 지오다타베이스 또는 지오코딩을 위해 이를 사용하여 각 그리드 셀에 고유 식별자를 할당할 수 있다.

지구본 참조 모델

DGG 개념에서 "글로브"는 엄밀한 의미론적 요소가 없지만, Geodsy에서 소위 "그리드 레퍼런스 시스템"은 기준점에 상대적인 정밀한 위치의 공간을 나누는 격자인데, 이것은 대략 "지오이드의 표준 모델"이다. 그래서, Geoid 역할에서, DGG에 의해 덮인 "글로브"는 다음 물체들 중 하나가 될 수 있다.

  • 그리드의 각 셀이 표준 Geoid에 대한 표면 위치 좌표와 표고를 가질 때 지구의 지형 표면. 예: 좌표(좌표, 좌표, 좌표, z)가 있는 격자. 여기서 z는 표고다.
  • 표준 지오이드 표면. z 좌표는 모든 그리드에 대해 0이므로 생략할 수 있다( (, λ).
    1687년 이전(뉴턴의 공국 간행물)의 고대 표준은 "기준 구"를 사용했는데, 오늘날에는 Geoid가 기준 타원체로 수학적으로 추상화된다.
    • 단순화된 Geoid: 때로는 오래된 지질 표준(예: SAD69) 또는 비지질 표면(예: 완벽한 구형 표면)을 채택해야 하며 그리드로 덮을 것이다. 이 경우 세포는 반드시 모호하지 않은 방법으로 표지를 붙여야 하며, (φ', λ'), 변환(φφ, ))⟾(φ', λ')을 알아야 한다.
  • 투영면. 일반적으로 지리적 좌표(지리적 좌표, 지리적 좌표)가 2D 데카르트 좌표(x, y)로 2D 매핑 평면에 투영된다(일부 왜곡)된다.

글로벌 모델링 프로세스로서, 현대의 DGG는 투영 프로세스를 포함할 때 실린더나 원뿔 고형물과 같은 표면을 피하여 불연속 및 지수화 문제를 유발하는 경향이 있다. "구형 투영은 지구의 정확한 토폴로지를 보존하기 때문에, 다루어야 할 특이점이나 불연속성이 없기 때문에,[1] 정규 다면체 및 구의 위상적 등가물은 DGG가 다루는 것으로 가장 유망한 옵션으로 이어졌다.[4]

DGG로 작업할 때 어떤 옵션이 채택되었는지 지정하는 것이 중요하다. 따라서 DGG 지구본의 기준 모델의 특성화는 다음과 같이 요약할 수 있다.

  • 복구된 개체: 전역 역할의 개체 유형. 투영이 없는 경우 그리드로 덮인 물체는 Geoid, Earth 또는 구체이며, 다른 것은 투영 표면의 기하학적 등급(예: 실린더, 큐브 또는 원뿔)이다.
  • 투영 유형: 없음(투영 없음) 또는 있음 존재하는 경우, 투영의 특성화는 투영의 목표 특성(예: 동일 면적, 등각 등)과 수정 기능의 등급(예: 삼각, 선형, 이차 등)으로 요약할 수 있다.

참고: DGG가 투영 표면을 커버하는 경우, 데이터 입증의 맥락에서 레퍼런스-Geoid에 대한 메타데이터도 중요하다. 일반적으로 투영 표면과의 혼동 없이 ISO 19111의 CRS 값을 알려준다.

유형 및 예제

DGG를 분류하거나 비교하기 위한 주요 구분 특성은 계층적 그리드 구조의 사용 여부다.

  • 계층적 참조 시스템에서 각 셀은 셀의 하위 집합에 대한 "상자 참조"이며, 셀 식별자는 번호를 매기는 논리나 구조에서 이 계층을 표현할 수 있다.
  • 비계층적 참조 시스템에서 각 셀은 구별되는 식별자를 가지며 공간의 고정 척도 영역을 나타낸다. 위도/경도 시스템의 탈고화가 가장 보편적이며, 변환에 대한 표준 참조가 된다.

DGG를 분류하는 다른 일반적인 기준은 타일 형태와 세분성(그리드 해상도):

  • 기와 규칙성 및 모양: 규칙성, 반규칙성 또는 불규칙한 격자가 있다. 일반 폴리곤에 의한 일반적인 틸팅과 마찬가지로 일반 면(벽 타일은 직사각형, 삼각형, 육각형 등)으로 타일링하거나 얼굴형은 같지만 크기나 각도를 변경하여 반정형 모양이 가능하다.
    형상의 균일성과 메트릭스의 규칙성은 더 나은 그리드 인덱싱 알고리즘을 제공한다. 비록 실용성은 떨어지지만, 보로노이 커버리지처럼 완전히 불규칙한 그리드가 가능하다.
  • 미세 또는 굵은 그래널링(셀 크기): 현대의 DGG는 그리드 분해능에서 파라메트리징이 가능하므로 최종 DGG 인스턴스의 특성이지만, DGG 유형이 특정 분해능을 사용해야 하거나 디스트리밍 한도를 가져야 하는 경우를 제외하고는 DGG를 분류하는 데 유용하지 않다. "미세" 과립 격자는 무제한이고 "코리"는 급격한 제한을 말한다. 역사적으로 주요 제한사항은 디지털/아날로그 미디어, 데이터베이스 내 그리드의 압축/확장 표현, 그리드를 저장하기 위한 메모리 제한과 관련이 있다. 정량적 특성화가 필요한 경우 그리드 셀의 평균 면적이나 셀 중심 간의 평균 거리를 채택할 수 있다.

비계층 그리드

이산 전역 그리드의 가장 일반적인 등급은 세포 중심점을 경도/위도 경맥과 평행도에 배치하거나, 직사각형 세포의 경계를 형성하기 위해 경도/위도 경맥과 평행도를 사용하는 등급이다. 모두 위도/경도를 기반으로 하는 그러한 그리드의 예:

UTM 영역:
지구를 60(스트립) 구역으로 나누고, 각각 경도 6도 띠를 이룬다. 디지털 미디어에서는 겹치는 영역을 제거한다. 각 구역에서 secant 가로 메르카토르 투영을 사용하십시오. 구역당 1개씩 60초짜리 실린더를 정의하십시오.
UTM 구역은 위도 대역을 추가하여 군사 그리드 기준 시스템(MGRS)에 의해 강화되었다. 		Utm-zones-USA.svg
인셉션: 1940년대 덮개가 있는 물체: 실린더(60개 옵션) 투영: UTM 또는 latlong 불규칙한 타일: 다각형 스트립 세밀도: 거칠다.
(현대) UTM - 범용 횡단 메르카토르:
연속 UTM 그리드의 탈바꿈이며, 2-수준 계층의 일종으로, 1단계 레벨(곡물 분석)이 "위도 대역이 있는 UTM 구역"(MGRS)에 해당하며, 기준-투영 객체와 동일한 60개의 실린더를 사용한다.
각 미세그레인 셀은 "그리드 존 지정자", "10만 미터 제곱 식별자" 및 "숫자 위치"에 의해 구성된 구조화된 ID에 의해 지정된다. 격자 분해능은 좌표에 있는 자릿수의 직접적인 함수로서, 또한 표준화된다. 예를 들어, 세포는 17N 630084 4833438 약 10mx10m의 제곱이다.
PS: 이 표준은 60개의 고유 실린더를 투영에 사용한다. 또한 "지역 횡단 메르카토르"(RTM 또는 UTM Regional)와 "지역 횡단 메르카토르"(LTM 또는 UTM Local) 표준이 있으며, 실린더가 보다 구체적이어서 관심 지점에서 더 잘 맞고 정밀하게 장착할 수 있다. 		Utmzonenugitterp.png
인셉션: 1950년대 덮개가 있는 물체: 실린더(60개 옵션) 투영: UTM 직사각형 타일: 등각(적합) 세분화: 미세
ISO 6709:
전통적인 "눈금" 표현과 현대적인 숫자로 조정된 셀 기반 위치를 확인한다. 세분성은 1도 눈금, .01도 눈금 등 숫자표현의 단순한 규약에 의해 고정되며 그리드를 통해 비등등 영역 셀이 발생한다. 세포의 모양은 삼각형인 극을 제외한 직사각형이다. 숫자 표현은 도(Annex D)와 십진수(Annex F)의 두 가지 주요 규약에 의해 표준화된다. 그리드 분해능은 자릿수(Annex H)에 의해 제어된다. 	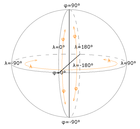	Geographic coordinates sphere.png
시작: 1983 덮개가 있는 개체: Geoid(ISO 19111의 CRS) 투영: 없음 직사각형 타일: 균일한 회전 모양 세분화: 미세
기본 DEM(TIN DEM):
벡터 기반 삼각 불규칙 네트워크(TIN) — TIN DEM 데이터 집합을 1차(측정된) DEM이라고도 한다. 많은 DEM은 위도와 경도의 일정한 각도 증분에 배치된 점의 격자 위에 생성된다. 예로는 Global 30 Arc-Second Iglation Dataset(GTOPO30)[5] 및 Global Multi-Deption Terminal Iglation Data 2010(GMTED2010)이 있다.[6]삼각형 불규칙 네트워크는 삼각형 전면으로 구성된 연속 표면을 나타낸다. 		Delaunay-Triangulation.svg
인셉션: 1970년대 덮개가 있는 물체: 지형 투영: 없음 삼각형이 아닌 타일: 파라메트리화(파라미터) 세분화: 미세
아라카와 그리드:
지구 환경 멀티스케일 모델(GEM)은 지구 기후 모델링에 아라카와 그리드를 사용한다.[7] 다른 DGG와 비교하기 위해 참조 DGG를 "A-grid"라고 부른다. 1980년대에 사용된 공간 해상도는 500x500까지 입니다.
인셉션: 1977 덮개가 있는 물체: 지오이드 투영: ? 직사각형 타일: 모수, 공간 시간 세분화: 중간
WMO 제곱:
NOAA가 고유하게 사용하는 특수 그리드는 위도 경도 격자선을 가진 세계의 차트를 각각 고유한 4자리 숫자 식별자를 가진 10° 위도의 그리드 셀로 나눈다(첫 번째 숫자는 사분원 NE/SE/SW/NW 식별).
인셉션: 2001 덮개가 있는 물체: 지오이드 투영: 없음 일반 타일: 36x18 직사각형 셀 세밀도: 거칠다.
월드 그리드 사각형:
일본 산업 표준(JIS X0410)에서 표준화된 일본 그리드 스퀘어의 호환 가능한 확장이다. World Grid Square 코드는 6개의 레이어를 기반으로 세계를 커버하는 격자 사각형을 식별할 수 있다. 격자 사각형은 해상도에 따라 6자리부터 13자리까지의 순서로 표현할 수 있다.[8]
인셉션: ? 덮개가 있는 물체: 지오이드 투영: ? ? 타일: ? 세분화: ?

계층 그리드

연속적인 공간 파티셔닝. 두 번째와 세 번째 지도에서 회색과 녹색의 격자는 계층적이다.

오른쪽 옆 그림에는 영국 해안의 3가지 경계 지도가 표시된다. 첫 번째 지도는 150km 크기의 셀이 있는 격자 레벨-0으로 덮여 있었다. 세부사항을 확대축소할 필요가 없는 중앙의 회색 셀만이 레벨 0으로 남아 있다; 두 번째 맵의 다른 모든 셀은 각각 75km의 4-셀-그리드(그리드 레벨 1)로 분할되었다. 세 번째 지도에서 12 셀 레벨-1은 회색으로 남아 있고, 다른 모든 셀은 다시 분할되었으며, 각 레벨-1 셀은 레벨 2-그리드(level-2-2)로 변환되었다.
계층적 그리드를 생성하는 이러한 재귀 프로세스를 사용하는 DGG의 예는 다음과 같다.

ISEA 이산 글로벌 그리드(ISEA DGG):
오레곤 주립 대학의 연구원들이 제안한 격자 등급이다.[1] 격자전지는 이코사면체 표면에 규칙적인 다각형으로 만들어진 다음, 이코사면체 스나이더 이퀄 에어리어(ISEA) 지도[9] 투영법을 사용하여 역투사하여 구체에 동일한 면적전지를 형성한다. 지구와 관련된 이코사면체의 방향은 다른 기준에 맞게 최적화될 수 있다.[10]

세포는 육각형, 삼각형 또는 사변형일 수 있다. 다중 분해능은 연속 분해능에서 조리개 또는 셀 영역 사이의 비율을 선택하여 표시한다. Some applications of ISEA DGGs include data products generated by the European Space Agency's Soil Moisture and Ocean Salinity (SMOS) satellite, which uses an ISEA4H9 (aperture 4 Hexagonal DGGS resolution 9),[11] and the commercial software Global Grid Systems Insight,[12] which uses an ISEA3H (aperture 3 Hexagonal DGGS).

인셉션: 1992년..2004 덮개가 있는 개체: ? 투영: 등면적 파라메트리된(파라미터, 삼각형 또는 4개 측광선) 타일: 동일 면적 세분화: 미세
COBE - 사각 구형 큐브:
큐브:[13] 구 tham HEALPix와 S2의 유사한 분해. 그러나 공간을 채우는 곡선을 사용하지 않고, 가장자리는 지오디컬이 아니며, 투영이 더 복잡하다.
인셉션: 1975년..1991 덮개가 있는 개체: 큐브 투영: 곡선 원근법 사각형 타일: 균일한 면적-변형 세분화: 미세
2차 삼각망사(QTM):
QTM은 구형 옥타헤드론의 4배 재귀분할에 의해 만들어진 삼각형 모양의 세포를 가지고 있다.[14][15]
인셉션: 1999... 2005 덮개가 있는 물체: 팔면체(또는 기타) 투영: 램버트의 등면적 원통형 삼각형 타일: 균일한 면적-배경 세분화: 미세
계층적 동일 영역 isoLatitude 픽셀레이션(HEALPix):
HEALPix는 동일한 면적 4각형 셀을 가지고 있으며, 원래 풀스카이 천체물리학 데이터 세트와 함께 사용하기 위해 개발되었다.[16]

일반적인 투영은 "H?4, K?3 HEALPix 투영"이다. S2와 동일한 인덱싱 틈새의 다른 부분과 비교한 주요 장점은 "구형 고조파 관련 계산에 적합하다".[17]

HealpixGridRefinement.jpg
인셉션: 2006 덮개가 있는 개체: 지오이드 투영: (K,H) 파라메타화된 HEALPix 투영 qradrrameter 타일: 균일한 구역-변환 세분화: 미세
계층적 삼각망사(HTM):
2003년 개발...2007년, HTM은 구의 다중 수준, 재귀적 분해다. 팔면체부터 시작해 레벨 0이 되게 해 팔면체의 가장자리를 (단위) 구에 투영하면 8개의 구면 삼각형이 생성되는데, 북방에는 4개, 남방에는 4개가 생성된다."[18] 각 삼각형은 4개의 하위 삼각형(1-4개 분할부터 4 분할). 첫 번째 공개 운영 버전은 2004년의 HTM-v2처럼 보인다[19]. 		HTM-diagram.png
인셉션: 2004 덮개가 있는 개체: 지오이드 투영: 없음 삼각형 타일: 구형 등각형 세분화: 미세
Geohash:
위도와 경도가 병합되어 결합된 숫자의 비트를 입력한다. 이진 결과는 base32로 표시되며, 사람이 판독할 수 있는 콤팩트한 코드를 제공한다. 공간 지수로 사용할 경우 Z 순서 곡선에 해당한다. Geohash-36 같은 변형도 있다. 		Four-level Z.svg
인셉션: 덮개가 있는 개체: 지오이드 투영: 없음 반정규 타일: 직사각형 세분화: 미세
S2 / S2Region:
"S2 그리드 시스템"은 "S2 지오메트리 라이브러리"[20]의 일부분이다(이 이름은 n-sphere, S²에 대한 수학적 표기법에서 유래한다). 구글에서 개발한 큐브 프로젝션과 공간을 채우는 힐버트 곡선을 기반으로 인덱스 시스템을 구현한다.[21][22] S2의 S2Region은 셀의 가장 일반적인 표현으로, 셀 위치와 미터법(예: 면적)을 계산할 수 있다. 각 S2Region은 서브그리드로서 31단계로 제한된다. 레벨 30 분해능은 1cm² 단위로 추정되며[23], 레벨 0은 85011012km²이다. 큐브 면(6면)의 계층적 그리드의 셀 식별자는 60비트의 ID를 가지고 있다. 따라서 "지구상의 모든 cm²는 64비트 정수를 사용하여 나타낼 수 있다." 		Hilbert Cubed Sphere.png
인셉션: 2015년 덮개가 있는 개체: 큐브 투영: 2차 함수를 사용한 각 입방체 면의 구형 투영 반정규 타일: 사방 투영 세분화: 미세
S2 / S2LatLng:
S2LatLng 표현에 의해 제공된 DGG는 ISO 6709 그리드처럼 계층적이고 그것의 특정 셀 모양을 가지고 있다.
인셉션: 2015년 덮개가 있는 개체: 지오이드 또는 구체 투영: 없음 반정규 타일: 사방형 세분화: 미세
S2 / S2CellId:
S2CellId 표현에 의해 제공된 DGG. 각 셀-ID는 모든 계층 수준에서 64비트 부호 없는 정수 고유 식별자다.
인셉션: 2015년 덮개가 있는 개체: 큐브 투영: ? 반정규 타일: 사방형 세분화: 미세

표준 등면적 계층 그리드

개방형 지리공간 컨소시엄(OGC)이 "Discrete Global Grid Systems"(DGGS)로 명명하는 계층형 DGG의 등급이 있으며, 이 등급은 18가지 요건을 충족해야 한다. 그 중에서도 이 세분류를 다른 계층적 DGG와 가장 잘 구분하는 것은 요구사항-8 "각 연속적인 그리드 정교화 수준과 각 셀 기하학에서 (...) 지정된 정밀도 수준 내에서 동일한 면적(...)인 셀"[24]이다.

DGGS는 항법용으로 원래 설계된 기존 좌표 참조 시스템과 구별되는 정보에 대한 프레임워크로 설계된다. 그리드 기반의 글로벌 공간정보 프레임워크가 분석 시스템으로서 효과적으로 작동하려면 지구의 표면을 균일하게 나타내는 셀을 사용하여 구성해야 한다.[24] DGGS 표준은 그 요건에 프레임워크가 제공해야 하는 일련의 기능과 작동을 포함한다.

모든 DGGS의 레벨 0 셀은 일반 다면체의 동일한 영역 면이다...

Regular polyhedra (top) and their corresponding equal area DGG

데이터베이스 모델링

모든 DGG 데이터베이스에서 그리드는 셀의 구성이다. 지역 및 중앙점은 대표적인 특성 또는 하위 분류로 설명된다. 셀 식별자(셀 ID)는 또한 지오코딩 애플리케이션에서 내부 인덱스 및/또는 (점 좌표 대신) 셀의 공개 라벨로 사용되는 중요한 속성이다. 때로는 MGRS 그리드에서와 같이 좌표가 ID의 역할을 하기도 한다.

대표성, 최적화, 모델링 대안이 많기 때문에 DGG가 많다. 모든 DGG 그리드는 그것의 셀들의 구성이고, 계층적 DGG에서 각각의 셀은 그것의 지역적 영역에 새로운 그리드를 사용한다.

이 그림은 데이터베이스가 셀 개념( 기하학적으로 삼각형 영역)을 사용하지 않고 노드와 에지: 각 노드는 표고이고 각 에지는 두 노드 사이의 거리인 TIN DEM 사례 및 유사한 "원시 데이터" 구조에 적합하지 않다.

일반적으로 DGG의 각 셀은 지역 점의 좌표(데이터베이스 표현의 중심점으로 표시됨)로 식별된다. 기능 상실로 "자유 식별자" 즉, 셀당 고유 번호나 고유한 기호 라벨인 셀 ID를 사용할 수도 있다. ID는 보통 공간지수(내부 쿼드트리나 k-d 트리 등)로 사용되지만, ID를 지오코딩 애플리케이션을 위해 사람이 판독할 수 있는 라벨로 변환하는 것도 가능하다.

최신 데이터베이스(예: S2 그리드 사용)는 동일한 데이터에 대해 여러 가지 표현을 사용하며, Geoid에 기반한 그리드(또는 셀 영역)와 투영에 기반한 그리드 기반 모두를 제공한다.

DGGS 프레임워크

이 표준은 그리드 작동 방법을 포함하여 계층적 DGG의 요구사항을 정의한다. 이러한 요건을 충족하는 모든 DGGG는 DGGS로 명명할 수 있다. "DGGS 규격에는 DGGS 핵심 개념 데이터 모델에서 정의한 DGGS 기준 프레임과 관련 기능 알고리즘이 포함되어야 한다."[25]

지구 그리드 시스템이 이 추상적 규격을 준수하려면, 그것은 두 가지 모두 여러 수준의 세분화로 지구 전체를 분할하고 전역 공간 기준 프레임을 제공하는 동일한 영역 셀의 계층적 다듬기를 정의해야 한다. 시스템은 또한 각 셀에 주소를 지정하고, 셀에 정량화된 데이터를 할당하며, 셀과 셀에 할당된 데이터에 대해 대수적 연산을 수행해야 한다. DGGS 핵심 개념 데이터 모델의 주요 개념:
  1. 기준 프레임 요소,
  2. 기능 알고리즘 요소, 구성 요소:
    1. 수량화 작업,
    2. 대수 연산,
    3. 상호운용성 운영.

역사

위도/경도의 평행선과 경맥으로 정의된 셀 영역을 가진 이산 전역 그리드는 지구 공간 컴퓨팅 초기부터 사용되어 왔다. 그 전에 종이 지도를 이용한 실용적 목적을 위한 연속 좌표의 탈바꿈은 오직 낮은 세분성으로만 일어났다. 아마도 이 사전 디지털 시대의 DGG의 가장 대표적인 예가 1940년대 군사 UTM DGG일 것이며, 지오코딩 목적을 위한 더 미세한 과립 세포 식별을 가지고 있을 것이다. 이와 유사하게 일부 계층적 그리드는 지리공간 컴퓨팅 이전에 존재하지만 굵은 그래널에만 존재한다.

지구 표면은 매일 지리적 지도에서 사용하기 위해 필요하지 않으며, 2000년대 이전에는 모든 행성 데이터를 같은 컴퓨터에 넣기 위해 매우 비쌌다. 첫 번째 디지털 글로벌 그리드는 위성 이미지의 데이터 처리와 글로벌(임계 및 해양학) 유체 역학 모델링에 사용되었다.

계층적 지오데틱 DGG 시스템에 대한 첫 번째 공개된 참조는 대기 모델링을 위해 개발되어 1968년에 출판된 시스템에 관한 것이다. 이 시스템들은 구면 이코사면체의 표면에 생성된 육각형 세포 영역을 가지고 있다. [26] [27]

공간 계층적 그리드는 Quadtree로서 주요 구조물이 이미지 인덱싱과 데이터베이스에 채택된 1980년대에 더욱 집중적인 연구의 대상이 되었다.[28]

이러한 그리드의 특정 사례가 수십 년 동안 사용되어 왔지만, 이산 글로벌 그리드라는 용어는 1997년[2] 오리건 주립대학의 연구자들에 의해 그러한 모든 실체의 등급을 설명하기 위해 만들어졌다.

… 2017년 OGC 표준화…

비교와 진화

서로 다른 두 곡선의 그리드 셀 식별자 스키마 비교, 모튼과 힐버트. 힐버트 커브(Hilbert curve)는 S2-지오메트리(S2-Geometry)와 같은 DGG, 지오하쉬(Geohash)와 같은 DGG의 모튼 커브(Morton curve)에서 채택되었다. 힐버트 곡선의 채택은 진화의 원인이었다. 왜냐하면 가장 가까운 세포를 이웃으로 보존하면서 덜 "점프"를 가지고 있기 때문이다.

평가 이산 글로벌 그리드는 면적, 형태, 소형성 등을 포함한 많은 측면으로 구성된다. 티쏘의 인디카트릭스와 같은 지도 투영을 위한 평가 방법은 이산 글로벌 그리드를 기반으로 한 지도 투영을 평가하는 데도 적합하다.

또한, 보완 프로파일 간의 평균 비율(AveRaComp)은 사각형 모양의 이산형 Global Grid에 대한 형상 왜곡을 잘 평가한다.

데이터베이스 개발 - 성능, 신뢰성 또는 정밀도를 높이기 위한 실질적인 요구에 따라 데이터베이스 개발 및 적응을 지향한다. 가장 좋은 선택은 DGG 아키텍처의 진화를 예언하면서 필수품에 선택되고 적응되는 것이다. 이러한 진화 과정의 예: 비계층적 DGGs에서 계층적 DGGs로, Geohash가 사용하는 Z-곡선 지수(숫자 간극을 기반으로 한 순진한 알고리즘)의 사용에서부터 S2와 같은 현대적 최적화에 사용되는 Hilbert-곡선 지수까지.

지오코드 변형

주요 기사: 지오코드

일반적으로 그리드의 각 셀은 지역 점의 좌표로 식별되지만, 좌표 구문과 의미론을 단순화하고, 고전적인 영숫자 그리드에서와 같이 식별자를 얻고, 식별자에서 지역 점의 좌표를 찾을 수도 있다. 소형 및 고속 조정 표현은 모든 DGG 솔루션에서 셀-ID 구현의 목표다.

좌표 대신 "자유 식별자"를 사용할 때, 즉 셀 ID인 지역 점당 고유 번호(또는 고유한 기호 라벨)를 사용할 때 기능 상실은 없다. 좌표를 사람이 읽을 수 있는 레이블로 변환하거나 레이블 길이를 압축하는 것은 그리드 표현에서 추가 단계다. 이 표현은 지오코드(geocode)라고 불린다.

행정 구역의 ISO 3166-1 알파-2 또는 지구 생태 구역의 롱허스트 코드로서 인기 있는 "글로벌 플레이스 코드"는 지구 커버리지의 일부에 속한다. 다른 한편으로는 특정 DGG의 모든 셀 식별자 세트를 "전체 탐지 가능 장소 코드"로 사용할 수 있다. 데이터 교환을 위한 표준으로 사용될 때 각각의 다른 ID 세트는 "지오코딩 시스템"으로 명명된다.

그리드의 셀 식별자(cell-ID)의 가치를 나타내는 방법에는 구조화 또는 단일화, 이진화 또는 인간 판독 가능 여부 등 여러 가지가 있다. 최소 경계 셀 또는 중앙 지점 셀로 대표되는 싱가포르의 머라이언 분수(약 5m 눈금 특징)와 같은 지도 특징을 가정하면 셀 ID는 다음과 같다.

셀 ID DGG 변종 이름 및 매개 변수 ID 구조, 그리드 분해능
(1° 17° 13.28° N, 103° 51° 16.88° E) ISO 6709/D 도(Annex ), CRS=WGS84 걸레에 걸다deg min sec dir) long ()deg min sec dir);
소수점 2자리 초
(1.286795, 103.854511) ISO 6709/F(십진수) 및 CRS=WGS 84 (lat,long); 6개의 소수점
(1.65AJ, 2V).IBCF) base36(비 ISO)의 십진수 ISO 6709/F 및 CRS=WGS 84 (lat,long); 4개의 소수점
w21z76281 Geohash, base32, WGS84 단일 문자, 9자
6PH57VP3+PR PlusCode, base20, WGS84 단일 문자, 10자
48N 372579 142283 UTM, 표준 소수점, WGS84 zone lat long; 3 + 6 + 6 숫자
48N 7ZHF 31SB UTM, 좌표 base36, WGS84 zone lat long; 3 + 4 + 4 자리

이러한 모든 지오코드는 지구상에서 같은 위치를 나타내며, 정밀도는 비슷하지만 문자열 길이, 구분자 사용 및 알파벳(비 구분 문자)이 다르다. 경우에 따라 "원래 DGG" 표현을 사용할 수 있다. 변형은 사소한 변화로, 예를 들어 숫자표현의 기초 또는 구조화된 부분을 단지 하나의 숫자표현이나 코드표현으로 교차시키는 등 최종표현에만 영향을 미친다. 가장 인기 있는 변형들은 지오코딩 어플리케이션에 사용된다.

영숫자 전역 그리드

사람이 판독할 수 있는 셀 식별자를 가진 DGG와 그 변형은 영숫자 그리드의 사실상의 표준으로 사용되어 왔다. 영숫자 기호로 한정되지 않고 '영숫자'가 가장 일반적인 용어다.

지오코드는 위치 및 DGG 컨텍스트에서 그리드 셀 ID를 나타내는 표기법이다. 디지털 표준과 DGG에는 지속적인 진화가 이루어지고 있기 때문에, 지난 몇 년 동안 각 지오코딩 협약의 인기에 있어서 지속적인 변화가 일어나고 있다. 더 넓은 채택은 또한 국가의 정부 채택, 인기 있는 지도 플랫폼에서의 사용, 그리고 많은 다른 요인에 달려 있다.

다음 목록에서 사용되는 예는 워싱턴 오벨리스크를 포함하는 "소형 그리드 셀"에 관한 것이다. 38° 53′ 22.11″ N, 77° 2′ 6.88″ W.

DGG 이름/var 인셉션 및 라이선스 변종 요약 설명 및 예제
UTM 영역/덮어지지 않음 1940년대 - CC0 겹치지 않고 독창적인 지구를 60개의 다각형으로 나눈다. 예: 18S
이산 UTM 1940년대 - CC0 원래 UTM 정수 지구를 60개의 영역으로 나누고, 각각은 경도 6도 띠를 이루며, 각 영역에 2분의 1의 횡단 메르카토르 투영법을 사용한다. 첫 번째 디지털 사용 및 규칙에 대한 정보 없음. 표준화가 나중에 ISO(1980년대)라고 가정한다. 예: 18S 323483 4306480
ISO 6709 1983 - CC0 원도표현. 격자 분해능은 숫자의 함수로서, 필요한 경우 선행 0이 채워지고, 그리드의 필요한 정밀도를 나타내기 위해 적절한 수의 숫자를 가진 소수 부분이다. 예: 38° 53′ 22.11″ N, 77° 2′ 6.88″ W.
ISO 6709 1983 - CC0 7자리 소수점 표시 데이터 구조가 "위도와 경도로 구성된 튜플은 2차원 지리적 위치를 나타낸다"는 XML 표현에 기초한 변종이며, 튜플의 각 숫자는 소수점 7자리 숫자로 구분된 실제 숫자다. 예: 38.889475, -77.035244.
맵코드 2001 - Apache2 독창적인 ISO 3166의 코드(국가 또는 도시)와 함께 혼합 코드를 최초로 채택한 경우. 2001년에 그 알고리즘은 특허권을 부여하는 아파치2의 허가를 받았다.
지오하시 2008 - CC0 독창적인 비트 인터레이스 latLong과 같으며, 결과는 base32로 표현된다.
거하시-36번길 2011 - CC0 독창적인 비슷한 이름에도 불구하고, Geohash와 같은 알고리즘을 사용하지 않는다. 6 X 6 그리드를 사용하고 각 셀에 문자를 연결한다.
What3words 2013년 특허 원본(영어) 3x3미터 정사각형을 3개의 영어 사전 단어로 변환한다.[30]
플러스코드 2014 - Apache2[31] 독창적인 또한 "Open Location Code"라는 이름이 붙었다. 코드는 기본 20개 번호로 도시 이름을 사용할 수 있어 도시의 경계 상자 코드 크기(맵코드 전략 등)에 따라 코드를 줄일 수 있다. 예: 87C4VXQ7+QV.
S2 셀 ID/베이스32 2015 - Apache2[32] base32로 표현된 원래 64비트 정수 계층적이고 매우 효과적인 데이터베이스 색인화. 그러나 PlusCode로서 base32 및 도시 프리픽스에 대한 표준 표현은 없다.
What3words/otherLang 2016년 … 2017년 - 특허 타국어 영어와 같지만, 다른 사전을 단어의 참고 자료로 사용한다.
포르투갈어 예 및 10x14m 셀: tenaz.fatual.davam.

기타 문서화된 시스템:

DGG 이름 인셉션 - 라이센스 요약 설명
C-제곱 2003 - "제한 없음" 라트롱 인터레이스 중간 사분면에 대한 추가 식별자를 포함한 ISO LatLong-di 표현 십진간격. 바이너리 인터레이싱이나 지오하시와 비교했을 때 "네이브" 알고리즘이다.
지오레프 ~ 1990 - CC0 ISO LatLong을 기반으로 하지만 보다 단순하고 간결한 표기법을 사용한다. "월드 지오그래픽 참조 시스템"은 지점 및 지역 식별을 위한 군사/항공 항법 좌표 시스템이다.
가스 2007 - 제한됨 미국/NGA 국립지질정보국(NGA)에서 개발한 참조 시스템. "DoD에 걸친 표준화된 전투공간 영역 참조 시스템으로서 전체 전투공간 파괴에 영향을 미칠 것"
WMO 사각형 2001년.. - CC0? 전문화된 NOAA의 이미지 다운로드 셀. ... 위도 경도 격자선을 가진 세계의 차트를 각각 고유한 4자리 숫자 식별자를 가진 10° 위도의 그리드 셀로 나눈다. 36x18 직사각형 셀(4자리 표시, 첫 번째 자리 식별 NE/SE/SW/NW).

참고 항목

참조

  1. ^ Jump up to: a b c d Sahr, Kevin; White, Denis; Kimerling, A.J. (2003). "Geodesic discrete global grid systems" (PDF). Cartography and Geographic Information Science. 30 (2): 121–134. doi:10.1559/152304003100011090.
  2. ^ Jump up to: a b Sahr, Kevin; White, Denis; Kimerling, A.J. (18 March 1997), "A Proposed Criteria for Evaluating Discrete Global Grids", Draft Technical Report, Corvallis, Oregon: Oregon State University
  3. ^ 제프리 더튼 "글로벌 위계적 테셀레이션이 무슨 큰일이냐?" 인용: "계층 테셀레이션, 글로벌 테셀레이션 또는 둘 다인 몇 가지 프로토타입 시스템"
  4. ^ "Overview".
  5. ^ "Global 30 Arc-Second Elevation (GTOPO30)". USGS. Archived from the original on July 10, 2017. Retrieved October 8, 2015.
  6. ^ "Global Multi-resolution Terrain Elevation Data 2010 (GMTED2010)". USGS. Retrieved October 8, 2015.
  7. ^ Arakawa, A.; Lamb, V.R. (1977). "Computational design of the basic dynamical processes of the UCLA general circulation model". Methods of Computational Physics. 17. New York: Academic Press. pp. 173–265.
  8. ^ "Research Institute for World Grid Squares". Yokohama City University. Retrieved November 21, 2017.
  9. ^ Snyder, J.P. (1992). "An equal-area map projection for polyhedral globes". Cartographica. 29 (1): 10–21. doi:10.3138/27h7-8k88-4882-1752.
  10. ^ Barnes, Richard (2019). "Optimal orientations of discrete global grids and the Poles of Inaccessibility". International Journal of Digital Earth. doi:10.1080/17538947.2019.1576786.
  11. ^ Suess, M.; Matos, P.; Gutierrez, A.; Zundo, M.; Martin-Neira, M. (2004). "Processing of SMOS level 1c data onto a discrete global grid". Proceedings of the IEEE International Geoscience and Remote Sensing Symposium: 1914–1917.
  12. ^ "Global Grid Systems Insight". Global Grid Systems. Retrieved October 8, 2015.
  13. ^ "LAMBDA - COBE Quadrilateralized Spherical Cube".
  14. ^ Dutton, G. (1999). A hierarchical coordinate system for geoprocessing and cartography. Springer-Verlag.
  15. ^ 반 스나이더 제트 추진 연구소. "분기 삼각망사: 지오프로세싱 및 카르토그래피용 위계 코르디네이트 시스템". 2016.
  16. ^ "HEALPix Background Purpose". NASA Jet Propulsion Laboratory. Retrieved October 8, 2015..
  17. ^ "S2 Cells".
  18. ^ "HTM Overview".
  19. ^ "ADASS 2003 Conference Proceedings".
  20. ^ "S2 Geometry".
  21. ^ "Overview". s2geometry.io. Retrieved 2018-05-11.
  22. ^ Kreiss, Sven (2016-07-27). "S2 cells and space-filling curves: Keys to building better digital map tools for cities". Medium. Retrieved 2018-05-11.
  23. ^ "S2 Cell Statistics".
  24. ^ Jump up to: a b Open Geospatial Consortium(2017), "Topic 21: 이산 글로벌 그리드 시스템 추상 사양". 문서 15-104r5 버전 1.0.
  25. ^ DGGS 표준의 섹션 6.1 "DGGS 핵심 데이터 모델 개요"
  26. ^ Sadourny, R.; Arakawa, A.; Mintz, Y. (1968). "Integration of the nondivergent barotropic vorticity equation with an icosahedral-hexagonal grid for the sphere". Monthly Weather Review. 96 (6): 351–356. CiteSeerX 10.1.1.395.2717. doi:10.1175/1520-0493(1968)096<0351:iotnbv>2.0.co;2.
  27. ^ Williamson, D.L. (1968). "Integration of the barotropic vorticity equation on a spherical geodesic grid". Tellus. 20 (4): 642–653. doi:10.1111/j.2153-3490.1968.tb00406.x.
  28. ^ [1]
  29. ^ Yan, Jin; Song, Xiao; Gong, Guanghong (2016). "Averaged ratio between complementary profiles for evaluating shape distortions of map projections and spherical hierarchical tessellations". Computers & Geosciences. 87: 41–55. doi:10.1016/j.cageo.2015.11.009.
  30. ^ "What3words: Find and share very precise locations via Google Maps with just 3 words". 2013-07-02. Retrieved 8 July 2014.
  31. ^ "Open Location Code is a library to generate short codes that can be used like street addresses, for places where street addresses don't exist.: Google/open-location-code". 2019-02-18.
  32. ^ "Computational geometry and spatial indexing on the sphere: Google/s2geometry". 2019-02-18.

외부 링크