k-d 트리

k-d 트리
k-d 트리
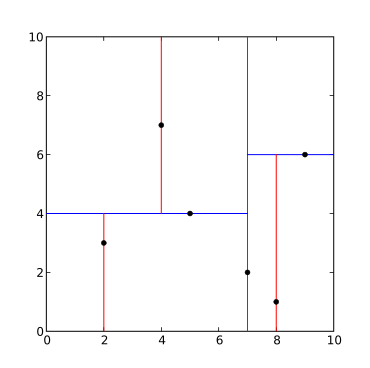
	3차원 K-D 트리입니다.첫 번째 분할(빨간색 수직면)은 루트 셀(흰색)을 2개의 서브 셀로 분할하고, 각 서브 셀(녹색 수평면)은 2개의 서브 셀로 분할합니다.마지막으로 4개의 셀이 (4개의 파란색 수직면에 의해) 2개의 서브셀로 분할됩니다.더 이상 분열이 없기 때문에, 마지막 8개는 잎 세포라고 불립니다.
유형	다차원 BST
발명된	1975
발명자	존 루이스 벤틀리
빅 O 표기의 시간 복잡도
알고리즘.
알고리즘.
공간
서치
삽입
삭제

컴퓨터 과학에서, k-d 트리(k-dimension tree의 줄임말)는 k-차원 공간에서 점을 구성하기 위한 공간 분할 데이터 구조이다. k-d 트리는 다차원 검색 키(예: 범위 검색 및 가장 가까운 이웃 검색)를 포함한 검색과 같은 여러 애플리케이션에 유용한 데이터 구조이다.k-d 트리는 이진 공간 분할 트리의 특별한 경우입니다.

묘사

k-d 트리는 모든 노드가 k차원 점인 이진 트리입니다.모든 비리프 노드는 공간을 두 부분으로 분할하는 분할 하이퍼플레인을 암묵적으로 생성하는 것으로 간주할 수 있습니다(반공간이라고 합니다).이 하이퍼플레인 왼쪽 포인트는 해당 노드의 왼쪽 서브트리로 표시되고 하이퍼플레인 오른쪽 포인트는 오른쪽 서브트리로 표시됩니다.하이퍼플레인 방향은 다음과 같은 방법으로 선택됩니다.트리의 모든 노드는 k차원 중 하나와 관련지어지며 하이퍼플레인 방향은 해당 차원의 축에 수직입니다.따라서 예를 들어 특정 분할에 대해 "x" 축을 선택하면 노드보다 작은 "x" 값을 가진 하위 트리의 모든 점이 왼쪽 하위 트리에 표시되고 더 큰 "x" 값을 가진 모든 점이 오른쪽 하위 트리에 표시됩니다.이 경우 하이퍼플레인은 점의 x값에 의해 설정되며, 그 정규값은 단위 x축이 ^[1]됩니다.

k-d 트리에 대한 작업

건설

축 정렬 분할 평면을 선택하는 방법은 다양하므로 k-d 트리를 구성하는 방법은 다양합니다.k-d 트리 구성의 표준 방법에는 다음과 같은 ^[2]제약이 있습니다.

트리를 내려갈 때 분할 평면을 선택하는 데 사용되는 축을 순환합니다.(예를 들어, 3차원 트리에서는 루트는 x-정렬 평면을 가지며 루트의 자녀는 모두 y-정렬 평면을 가지며 루트의 증손자는 모두 z-정렬 평면을 가지며 루트의 증손자는 모두 x-정렬 평면을 가진다.)eroot의 증손자들은 모두 Y자형 평면을 갖게 됩니다.)
분할 평면을 작성하는 데 사용되는 축의 좌표에 대해 하위 트리에 넣을 점의 중위수를 선택하여 점을 삽입합니다.(n개의 포인트 세트를 모두 알고리즘에 사전에 입력한다는 전제에 주의해 주세요).

이 방법은 균형 잡힌 k-d 트리로 이어지며, 이 트리에서 각 리프 노드는 루트로부터 거의 같은 거리에 있습니다.그러나 균형 잡힌 트리가 모든 애플리케이션에 최적인 것은 아닙니다.

중앙점을 선택할 필요는 없습니다.중위수를 선택하지 않은 경우에는 트리의 균형이 유지된다는 보장이 없습니다.복잡한 O(n) 중위수 검색^[3]^[4] 알고리즘을 코딩하거나 힙소트 또는 병합소트 등의 O(n log n) 정렬을 사용하여 모든 n개의 점을 정렬하지 않도록 하려면 랜덤으로 선택한 고정 수의 점을 정렬하고 해당 점의 중위수를 분할 평면으로 사용하는 것이 일반적입니다.실제로, 이 기술은 종종 나무의 균형을 잘 잡는 결과를 낳습니다.

n개의 점 목록이 주어지면 다음 알고리즘은 중위수 검색 정렬을 사용하여 해당 점을 포함하는 균형 잡힌 k-d 트리를 구성합니다.

함수 kdtree(점 목록, int 깊이) {// 모든 유효한 값 var int 축을 순환하도록 깊이에 따라 축을 선택합니다. := depth mod k;/// 점 목록을 정렬하고 pointList에서 축별로 중앙값을 선택한 피벗 요소로 중앙값을 선택합니다. // 노드를 만들고 하위 트리 노드를 구성합니다. := median; node.왼쪽.Child:= kdtree(중위수 앞의 점, 깊이+1); node.rightChild := kdtree(중위수 뒤의 점, 깊이+1); 리턴 노드; }

일반적으로 중위수 뒤에 있는 점은 현재 치수의 중위수보다 엄격하게 큰 점만 포함합니다.현재 치수의 중위수에 있는 점의 경우 모든 차원에서 점을 비교하는 함수를 정의할 수 있습니다.예를 들어, 점을 "보다 작은" 부분 집합과 "보다 크거나 같은" 부분 집합으로 분할하여 중앙값과 동일한 점을 중앙값의 한쪽에 둘 수 있습니다.

이 알고리즘은 임의의 노드에 대해 왼쪽 서브트리의 모든 노드가 분할 플레인의 한쪽에 있고 오른쪽 서브트리의 모든 노드가 다른 쪽에 있다는 불변성을 작성합니다.분할 평면에 있는 점은 양쪽에 나타날 수 있습니다.노드의 분할 플레인은 해당 노드에 관련되어 있는 포인트(코드에서는 node.location이라고 부릅니다)를 통과합니다.

균형 잡힌 k-d 트리를 구축하기 위한 대체 알고리즘은 트리를 구축하기 전에 데이터를 사전 정렬한다.그런 다음, 그들은 나무 건설 중에 사전 정렬 순서를 유지하며, 따라서 각 세분화 수준에서 중앙값을 찾는 비용이 많이 드는 단계를 제거한다.이러한 두 가지 알고리즘은 3차원 컴퓨터 그래픽에 대한 광선 추적 실행 시간을 개선하기 위해 삼각형을 정렬하는 균형 잡힌 k-d 트리를 구축한다.이러한 알고리즘은 k-d 트리를 구축하기 전에 n개의 삼각형을 사전 정렬한 다음 최적의 ^[5]^[6]경우 O(n log n) 시간 내에 트리를 구축합니다.균형 잡힌 k-d 트리를 구축하여 포인트를 정렬하는 알고리즘은 최악의 경우 복잡도는 O(kn log n)^[7]^[8]입니다.이 알고리즘은 트리를 구축하기 전에 Humpsort 또는 Mergesort 등의 O(n log n) 정렬을 사용하여 각 k차원에서 n개의 포인트를 유지합니다.그런 다음 트리 구성 중에 이러한 k개의 순서를 유지하며, 따라서 각 세분화 수준에서 중앙값을 찾는 것을 피한다.

구현 예시

Python 프로그래밍 언어로 구현된 위의 알고리즘은 다음과 같습니다.

부터 수집품 수입품 명명된 태플 부터 교환입니다. 수입품 아이템게터 부터 인쇄하다 수입품 포맷  학급 노드(명명된 태플("노드", "Location left_child right_child")):     방어하다 __repr__(자신):         돌아가다 포맷(태플(자신))  방어하다 kdtree(포인트_리스트, 깊이: 인트 = 0):     한다면 것은 아니다. 포인트_리스트:         돌아가다 없음.      k = 렌(포인트_리스트[0])  #는 모든 점의 치수가 동일하다고 가정합니다.     # 모든 유효한 값을 축이 순환하도록 깊이에 따라 축 선택     축. = 깊이 % k      # 축별로 점 리스트를 정렬하고 중앙값을 피벗 요소로 선택합니다.     포인트_리스트.종류(열쇠=아이템게터(축.))     중앙값 = 렌(포인트_리스트) // 2      # 노드 작성 및 서브트리 구축     돌아가다 노드(         위치=포인트_리스트[중앙값],         왼쪽_자녀=kdtree(포인트_리스트[:중앙값], 깊이 + 1),         오른쪽 아이=kdtree(포인트_리스트[중앙값 + 1 :], 깊이 + 1),     )  방어하다 주된():     「사용 예」     포인트_리스트 = [(7, 2), (5, 4), (9, 6), (4, 7), (8, 1), (2, 3)]     트리 = kdtree(포인트_리스트)     인쇄물(트리)  한다면 __name__ == "_메인__":     주된()

출력은 다음과 같습니다.

((7, 2), ((5, 4), ((2, 3), 없음, 없음), ((4, 7), 없음, 없음), (9, 6), ((8, 1), 없음, 없음), 없음)

생성된 트리는 다음과 같습니다.

점 집합에 대한 k-d 트리 분해
(2,3), (5,4), (9,6), (4,7), (8,1), (7,2).

결과 k-d 트리.

요소 추가

다른 검색 트리에 요소를 추가하는 것과 같은 방법으로 k-d 트리에 새 점을 추가합니다.먼저 삽입할 점이 분할 평면의 "왼쪽" 또는 "오른쪽"에 있는지 여부에 따라 루트에서 시작하여 왼쪽 또는 오른쪽 아이로 이동합니다.하위 노드를 배치해야 하는 노드에 도달하면 새 노드를 포함하는 노드의 분할 평면의 어느 쪽에 따라 새 지점을 리프 노드의 왼쪽 또는 오른쪽 하위 항목으로 추가합니다.

이 방법으로 포인트를 추가하면 트리가 불균형 상태가 되어 트리 성능이 저하될 수 있습니다.트리 성능 저하 속도는 추가되는 트리 포인트의 공간 분포와 트리 크기에 대해 추가된 포인트 수에 따라 달라집니다.트리가 너무 불안정해지면 트리 밸런싱에 의존하는 쿼리(가장 가까운 네이버 검색 등)의 성능을 복원하기 위해 트리를 재조정해야 할 수 있습니다.

요소 제거

기존 k-d 트리에서 점을 제거하고 불변성을 유지하려면 대상 노드의 자식에서 모든 노드와 리프의 집합을 형성하고 트리의 해당 부분을 재생성하는 것이 가장 쉬운 방법입니다.

또 다른 접근법은 ^[9]제거된 지점을 대체하는 방법을 찾는 것입니다.먼저 삭제할 점을 포함하는 노드 R을 찾습니다.R이 리프 노드인 기본 케이스의 경우 교체할 필요가 없습니다.일반적인 경우 R에 루트된 서브트리에서 대체 포인트(예를 들어 p)를 찾습니다.R에 저장된 점을 p로 바꿉니다.그런 다음 p를 재귀적으로 제거합니다.

대체점을 찾기 위해 R이 x를 구별하고 R이 올바른 아이를 갖는 경우 오른쪽 아이에 뿌리를 둔 하위 트리에서 최소 x 값을 가진 점을 찾습니다.그렇지 않으면 왼쪽 아이에 루트된 하위 트리에서 최대 x 값을 가진 점을 찾습니다.

밸런스

k-d 트리의 균형은 k-d 트리가 다차원으로 정렬되기 때문에 불변성을 깨뜨릴 수 있기 때문에 트리 회전 기법을 사용하여 균형을 맞출 수 없기 때문에 주의가 필요하다.

균형 잡힌 k-d 트리의 여러 변형이 존재한다.여기에는 분할된 k-d 트리, 의사 k-d 트리, K-D-B 트리, hB 트리 및 Bkd 트리가 포함됩니다.이러한 변형 중 많은 수가 적응형 k-d 나무이다.

가장 가까운 네이버 검색

2-d 트리에서 가장 가까운 네이버 검색의 예.여기서 트리는 이미 구축되어 있고, 각 노드는 직사각형에 대응하고, 각 직사각형은 2개의 동일한 서브직선으로 분할되어 있으며, 잎은 단일 점을 포함하는 직사각형에 대응하고 있다.

NN(Neighbor Search) 알고리즘은 트리에서 특정 입력점에 가장 가까운 점을 찾는 것을 목표로 합니다.이 검색은 트리 속성을 사용하여 검색 공간의 대부분을 빠르게 제거함으로써 효율적으로 수행할 수 있습니다.

k-d 트리에서 가장 가까운 네이버 검색은 다음과 같이 진행됩니다.

루트 노드부터 시작하여 알고리즘은 검색 포인트가 삽입될 때와 같은 방식으로 트리를 재귀적으로 아래로 이동합니다(즉, 점이 분할 차원의 현재 노드보다 작거나 큰지 여부에 따라 왼쪽 또는 오른쪽으로 이동합니다).
알고리즘이 리프 노드에 도달하면 노드 포인트를 확인하고 거리가 "현재 최선"보다 더 좋은 경우 해당 노드 포인트가 "현재 최선"으로 저장됩니다.
알고리즘은 트리의 재귀를 해제하고 각 노드에서 다음 단계를 수행합니다.
1. 현재 노드가 현재 최선 노드보다 가까우면 현재 최선 노드가 됩니다.
2. 알고리즘은 분할 평면의 다른 쪽에 현재 최량보다 검색 지점에 더 가까운 점이 있는지 확인합니다.개념적으로 이는 현재 가장 가까운 거리와 동일한 반지름을 가진 검색점 주변의 하이퍼스피어와 분할하는 하이퍼플레인을 교차시킴으로써 이루어집니다.하이퍼플레인은 모두 축방향으로 정렬되어 있기 때문에 이는 검색점과 현재 노드의 분할 좌표 사이의 거리가 검색점에서 현재 최선까지의 거리(전체 좌표)보다 작은지 여부를 확인하기 위한 단순한 비교로 구현됩니다.
  1. 하이퍼스피어가 평면을 통과할 경우 평면의 다른 쪽에 더 가까운 지점이 있을 수 있으므로 알고리즘은 전체 검색과 동일한 재귀 프로세스를 따라 더 가까운 지점을 찾는 현재 노드에서 트리의 다른 분기를 아래로 이동해야 합니다.
  2. 하이퍼스피어가 분할 평면과 교차하지 않으면 알고리즘은 트리를 계속 걸어 올라가 노드 반대편에 있는 가지 전체가 제거됩니다.
알고리즘이 루트 노드에 대해 이 프로세스를 완료하면 검색이 완료됩니다.

일반적으로 알고리즘은 제곱근 계산을 피하기 위해 비교에 제곱근 거리를 사용합니다.또한 비교를 위해 변수의 전류 최적 거리 제곱을 유지함으로써 계산을 절약할 수 있습니다.

알고리즘은 간단한 변경으로 여러 가지 방법으로 확장할 수 있습니다.1개 대신 k개의 현재 베스트를 유지함으로써 한 점에 가장 가까운 k개의 네이버를 제공할 수 있습니다.분기는 k개의 점이 발견되고 분기가 k개의 현재 최량점보다 가까운 점을 가질 수 없는 경우에만 제거됩니다.

또한 더 빨리 실행되도록 근사 알고리즘으로 변환할 수도 있습니다.예를 들어 트리에서 검사할 수 있는 개수의 상한을 설정하거나 실시간클락에 기반한 검색 프로세스를 중단하는 것(하드웨어 구현에 더 적합할 수 있음)으로 대략적인 근접 검색을 수행할 수 있습니다.그 결과 거리가 0인 노드에 대한 정밀도를 업데이트하지 않으면 트리에 이미 있는 포인트의 가장 가까운 인접 라우터를 얻을 수 있습니다.이 때문에, 일의는 아니지만, 원래의 검색 포인트와 같은 위치에 있는 포인트는 폐기되는 단점이 있습니다.

최적의 지점을 철저히 검색하지 않음으로써 상당한 속도 향상으로 인해 로봇 공학 같은 실시간 애플리케이션에서 가장 가까운 이웃이 유용합니다.구현 중 하나는 best-bin-first 검색입니다.

범위 검색

범위 검색은 파라미터의 범위를 검색합니다.예를 들어 나무가 소득과 연령에 해당하는 값을 저장하는 경우 범위 검색은 20세에서 50세 사이의 연령과 50,000세에서 80,000세 사이의 소득을 가진 트리의 모든 구성원을 찾는 것과 비슷할 수 있습니다.k-d 트리는 트리의 각 수준에서 도메인의 범위를 반으로 나누기 때문에 범위 검색을 수행하는 데 유용합니다.

이진 검색 트리의 분석 결과, n개의 노드를 포함하는 k-차원 k-d 트리에서 범위 검색에 대한 최악의 시간은 ^[10]다음 방정식으로 주어진다.

t_{\text{filename}}}=O\left(k\cdot n^{1-{\frac {1}{k}}\right)

고차원 데이터에 의한 성능 저하

일반적으로 분석이 ^[11]까다롭지만 랜덤하게 분포된 점의 경우 가장 가까운 점을 찾는 것이 평균 O(log n) 연산입니다.

고차원 공간에서는 차원성의 저주로 인해 알고리즘이 저차원 공간보다 더 많은 지점을 방문해야 합니다.특히 점의 수가 차원 수보다 약간 많은 경우 알고리즘은 모든 점을 선형으로 검색하는 것보다 약간만 우수합니다.일반적으로 치수가 k이면 데이터의 점 수 n은 n ÷ 2가^k 되어야 한다.그렇지 않으면, k-d 트리를 고차원 데이터와 함께 사용할 때 트리의 대부분의 포인트가 평가되고 효율은 철저한 ^[12]검색과 다를 바 없으며, 충분한 빠른 답변이 필요한 경우 대신 근사 가장 가까운 이웃 방법을 사용해야 한다.

쿼리 포인트가 k-d 트리의 포인트와 멀리 떨어져 있는 경우 성능 저하

또한 저차원 공간에서도 쿼리 포인트의 k개의 가장 가까운 인접 라우터 간의 평균 쌍별 거리가 쿼리 포인트와 각 k개의 가장 가까운 인접 라우터 간의 평균 거리보다 현저히 작을 경우 쿼리 포인트에서 로의 거리가 선형으로 저하되기 때문에 가장 가까운 인접 라우터 검색의 성능이 저하됩니다.각각의 가장 가까운 인접 라우터의 크기는 비슷합니다.최악의 경우 원점을 중심으로 한 구면의 표면에 분포된 점 구름을 고려합니다.모든 포인트는 원점에서 등거리에 있기 때문에 원점에서 가장 가까운 네이버를 검색하려면 구면상의 모든 포인트에서 반복해야 합니다.이 경우 가장 가까운 네이버를 특정할 수 있습니다).

최악의 경우 k-d 트리 검색의 잠재적으로 현저한 성능 저하를 완화하기 위해 최대 거리 파라미터를 트리 검색 알고리즘에 제공할 수 있으며, 트리의 특정 분기 중 가장 가까운 점이 이 최대 거리보다 가까이 있을 수 없을 때마다 재귀 검색을 플루닝할 수 있습니다.이로 인해 가장 가까운 네이버 검색에서 가장 가까운 네이버를 반환하지 못할 수 있습니다.즉, 쿼리 포인트로부터 이 최대 거리 내에 포인트가 없는 것을 의미합니다.

복잡성

n개의 포인트에서 정적 k-d 트리를 구축하면 다음과 같은 최악의 복잡성이 발생합니다.
- O(n log n) Humpsort 또는 Mergesort와 같은 O²(n log n) 정렬을 사용하여 초기 트리의 각 수준에서 중앙값을 찾는 경우
- O(n log n) 중위수 알고리즘을^[3]^[4] 사용하여 초기 트리의 각 수준에서 중위수를 선택하는 경우
- k-d ^[8]트리를 구축하기 전에 Humpsort 또는 Mergesort 등의 O(n log n) 정렬을 사용하여 각 k차원에서 n개의 포인트가 사전 정렬된 경우 O(kn log n).
균형 잡힌 k-d 트리에 새 점을 삽입하려면 O(log n) 시간이 걸립니다.
균형 잡힌 k-d 트리에서 점을 제거하려면 O(log n) 시간이 걸립니다.
균형 잡힌 k-d 트리에서 축 병렬 범위를 쿼리하려면 O(n^1−1/k +m) 시간이 걸립니다. 여기서 m은 보고된 점의 수이고 k는 k-d 트리의 치수입니다.
랜덤하게 분포된 포인트가 있는 균형 잡힌 k-d 트리에서 가장 가까운 이웃을 1개 찾는 데 평균 O(log n) 시간이 걸린다.

바리에이션

볼륨 측정 객체

점 대신 k-d 트리는 직사각형 또는 ^[13]^[14]초직각형을 포함할 수도 있습니다.따라서 범위 검색은 검색 직사각형과 교차하는 모든 직사각형을 반환하는 문제가 됩니다.나무는 잎사귀에 직사각형이 있는 일반적인 방식으로 만들어져 있다.직교 범위 검색에서는 중앙값과 비교할 때 반대 좌표가 사용됩니다.예를 들어 현재 레벨이 x를 따라_high 분할된 경우 검색 직사각형의_low x 좌표를 확인합니다.중위수가 검색 직사각형의 x좌표보다_low 작을 경우 왼쪽 가지에 있는 직사각형이 검색 직사각형과 교차할 수 없으므로 제거할 수 있습니다.그렇지 않으면 두 지점을 모두 통과해야 합니다.1차원 특수 케이스인 간격 트리를 참조하십시오.

잎만 포인트

잎에만 ^[2]점이 저장된 k-d 트리를 정의할 수도 있습니다.이러한 형태의 k-d 트리는 표준 중위수 분할을 제외한 다양한 분할 역학을 허용합니다.중간점 분할^[15] 규칙은 점의 분포에 관계없이 검색할 공간의 가장 긴 축 가운데를 선택합니다.이렇게 하면 가로 세로 비율이 최대 2:1이 되지만 깊이는 점의 분포에 따라 달라집니다.슬라이딩 중간점이라고 하는 변형은 분할의 양쪽에 점이 있는 경우에만 중간에 분할됩니다.그렇지 않으면 중앙에서 가장 가까운 지점에서 분할됩니다.Maneewongvatana 및 Mount는 일반적인 데이터 세트에서 "충분한" 성능을 제공함을 보여줍니다.

슬라이딩 미드포인트를 사용하면 근접 근접 쿼리에 대해 O $O\left({\tfrac {1}{{\epsilon \ }^{d}}}\log n\right)$ 1µ $O\left({\tfrac {1}{{\epsilon \ }^{d}}}\log n\right)$ $O\left({\tfrac {1}{{\epsilon \ }^{d}}}\log n\right)$ display $)\$ O $\left({\tfrac {1}{\epsilon \}^{d}}\log n\$ right $O\left({\tfrac {1}{{\epsilon \ }^{d}}}\log n\right)$ 로 응답할 수 있습니다.O $($ + $O\left(\log n+{\left({\tfrac {1}{\epsilon \ }}\right)}^{d}\right)$ ( $O\left(\log n+{\left({\tfrac {1}{\epsilon \ }}\right)}^{d}\right)$ 1 $display$ ) display $style display$ $lon \}\right)}^{d}\right)}$ 이 $O\left(\log n+{\left({\tfrac {1}{\epsilon \ }}\right)}^{d}\right)$ 메서드를 사용합니다.

「」를 참조해 주세요.

변형 닫기:

암묵적 k-d 트리, 명시적으로 정의된 분할 집합이 아닌 암묵적 분할 함수에 의해 정의된 k-d 트리
min/max k-d 트리, 각 노드에 최소값과 최대값을 관련짓는 k-d 트리
완화 k-d 트리, 각 노드의 판별자가 임의인 k-d 트리

오픈 소스 구현

ALGLIB에는 k-d 트리 기반의 가장 가까운 네이버 및 대략적인 가장 가까운 네이버알고리즘의 C# 및 C++ 실장이 있습니다.
CGAL 계산 알고리헴 라이브러리는 k-d 트리 기반 가장 가까운 이웃, 근사 가장 가까운 이웃 및 범위 검색 알고리즘을 구현합니다.
SciPy는 과학 컴퓨팅을 위한 Python 라이브러리이며 k-d 트리 기반의 가장 가까운 네이버 검색 알고리즘의 구현을 포함합니다.
머신러닝용 Python 라이브러리 skikit-learn에는 가장 가까운 네이버 및 radius 네이버 검색을 지원하는 k-d 트리의 구현이 포함되어 있습니다.

레퍼런스

^ Bentley, J. L. (1975). "Multidimensional binary search trees used for associative searching". Communications of the ACM. 18 (9): 509–517. doi:10.1145/361002.361007. S2CID 13091446.
^ ^a ^b Berg, Mark de; Cheong, Otfried; Kreveld, Marc van; Overmars, Mark (2008). "Orthogonal Range Searching". Computational Geometry. pp. 95–120. doi:10.1007/978-3-540-77974-2_5. ISBN 978-3-540-77973-5.
^ ^a ^b Blum, M.; Floyd, R. W.; Pratt, V. R.; Rivest, R. L.; Tarjan, R. E. (August 1973). "Time bounds for selection" (PDF). Journal of Computer and System Sciences. 7 (4): 448–461. doi:10.1016/S0022-0000(73)80033-9.
^ ^a ^b Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. Introduction to Algorithms. MIT Press and McGraw-Hill. 10장
^ Wald I, Havran V (September 2006). "On building fast kd-trees for ray tracing, and on doing that in O(N log N)" (PDF). In: Proceedings of the 2006 IEEE Symposium on Interactive Ray Tracing: 61–69. doi:10.1109/RT.2006.280216. ISBN 1-4244-0693-5. S2CID 1603250.
^ Havran V, Bittner J (2002). "On improving k-d trees for ray shooting" (PDF). In: Proceedings of the WSCG: 209–216.
^ Procopiuc, T; Agarwal, M; Arge, L; Vittner, J (2003). "Bkd-tree: A dynamic scalable kd-tree". In Hadzilacos, T; Manolopoulos, Y; Roddick, J; Theodoridis, Y (eds.). Lecture Notes in Computer Science. Vol. 2750. Berlin: Springer-Verlag. pp. 46–65.
^ ^a ^b Brown R (2015). "Building a balanced k-d tree in $O(kn log n)$ time". Journal of Computer Graphics Techniques. 4 (1): 50–68.
^ 찬드란, 샤랏kd-tree의 개요메릴랜드 대학교 컴퓨터과학과.
^ Lee, D. T.; Wong, C. K. (1977). "Worst-case analysis for region and partial region searches in multidimensional binary search trees and balanced quad trees". Acta Informatica. 9. doi:10.1007/BF00263763. S2CID 36580055.
^ Freidman, J. H.; Bentley, J. L.; Finkel, R. A. (1977). "An Algorithm for Finding Best Matches in Logarithmic Expected Time". ACM Transactions on Mathematical Software. 3 (3): 209. doi:10.1145/355744.355745. OSTI 1443274. S2CID 10811510.
^ Jacob E. Goodman, Joseph O'Rourke and Piotr Indyk, ed. (2004). "Chapter 39: Nearest neighbours in high-dimensional spaces". Handbook of Discrete and Computational Geometry (2nd ed.). CRC Press.
^ Rosenberg, J. B. (1985). "Geographical Data Structures Compared: A Study of Data Structures Supporting Region Queries". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 4: 53–67. doi:10.1109/TCAD.1985.1270098. S2CID 31223074.
^ Houthuys, P. (1987). "Box Sort, a multidimensional binary sorting method for rectangular boxes, used for quick range searching". The Visual Computer. 3 (4): 236–249. doi:10.1007/BF01952830. S2CID 3197488.
^ S. Maneewongvatana와 D. 엠마운트친구들이 뚱뚱하다면 마른 것도 괜찮아.제4회 CGC 연산기하학 워크숍, 1999.

[1] Bentley, J. L. (1975). "Multidimensional binary search trees used for associative searching". Communications of the ACM. 18 (9): 509–517. doi:10.1145/361002.361007. S2CID 13091446.

[compgeom-2] Berg, Mark de; Cheong, Otfried; Kreveld, Marc van; Overmars, Mark (2008). "Orthogonal Range Searching". Computational Geometry. pp. 95–120. doi:10.1007/978-3-540-77974-2_5. ISBN 978-3-540-77973-5.

[blum-3] Blum, M.; Floyd, R. W.; Pratt, V. R.; Rivest, R. L.; Tarjan, R. E. (August 1973). "Time bounds for selection" (PDF). Journal of Computer and System Sciences. 7 (4): 448–461. doi:10.1016/S0022-0000(73)80033-9.

[cormen-4] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L. Introduction to Algorithms. MIT Press and McGraw-Hill. 10장

[5] Wald I, Havran V (September 2006). "On building fast kd-trees for ray tracing, and on doing that in O(N log N)" (PDF). In: Proceedings of the 2006 IEEE Symposium on Interactive Ray Tracing: 61–69. doi:10.1109/RT.2006.280216. ISBN 1-4244-0693-5. S2CID 1603250.

[6] Havran V, Bittner J (2002). "On improving k-d trees for ray shooting" (PDF). In: Proceedings of the WSCG: 209–216.

[7] Procopiuc, T; Agarwal, M; Arge, L; Vittner, J (2003). "Bkd-tree: A dynamic scalable kd-tree". In Hadzilacos, T; Manolopoulos, Y; Roddick, J; Theodoridis, Y (eds.). Lecture Notes in Computer Science. Vol. 2750. Berlin: Springer-Verlag. pp. 46–65.

[knlogn-8] Brown R (2015). "Building a balanced k-d tree in $O(kn log n)$ time". Journal of Computer Graphics Techniques. 4 (1): 50–68.

[9] 찬드란, 샤랏kd-tree의 개요메릴랜드 대학교 컴퓨터과학과.

[Lee1977-10] Lee, D. T.; Wong, C. K. (1977). "Worst-case analysis for region and partial region searches in multidimensional binary search trees and balanced quad trees". Acta Informatica. 9. doi:10.1007/BF00263763. S2CID 36580055.

[Friedman:1977:AFB:355744.355745-11] Freidman, J. H.; Bentley, J. L.; Finkel, R. A. (1977). "An Algorithm for Finding Best Matches in Logarithmic Expected Time". ACM Transactions on Mathematical Software. 3 (3): 209. doi:10.1145/355744.355745. OSTI 1443274. S2CID 10811510.

[12] Jacob E. Goodman, Joseph O'Rourke and Piotr Indyk, ed. (2004). "Chapter 39: Nearest neighbours in high-dimensional spaces". Handbook of Discrete and Computational Geometry (2nd ed.). CRC Press.

[13] Rosenberg, J. B. (1985). "Geographical Data Structures Compared: A Study of Data Structures Supporting Region Queries". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 4: 53–67. doi:10.1109/TCAD.1985.1270098. S2CID 31223074.

[14] Houthuys, P. (1987). "Box Sort, a multidimensional binary sorting method for rectangular boxes, used for quick range searching". The Visual Computer. 3 (4): 236–249. doi:10.1007/BF01952830. S2CID 3197488.

[midpointsplit-15] S. Maneewongvatana와 D. 엠마운트친구들이 뚱뚱하다면 마른 것도 괜찮아.제4회 CGC 연산기하학 워크숍, 1999.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

v t 트리 데이터 구조
트리 검색 (다이나믹 세트/어소시에이션 어레이)	2–3 2–3–4 AA (a, b) AVL B B+ B* B^x. (최적) 바이너리 검색 춤추다 HTree 간격 주문통계 (좌향) 레드-블랙 희생양 스플라이 T 나무 UB 무게 밸런스
수북이	바이너리 이항 브로달 피보나치 좌파 페어링 스큐 판 엠데 보아스 약한
시도하다	Ctrie C-trie(압축 ADT) 해시 기수 서픽스 삼진수 검색 X-Fast 고속
공간 데이터 파티션 트리	공 BK BSP 데카르트어 힐베르트 R k-d(표준 k-d) M 미터법 MVP 옥트리 PH 우선 순위 R 쿼드 R R+ R* 부분 부사장 X
기타 트리	덮다 지수 펜윅 손가락. 프랙탈 트리 인덱스 퓨전 해시 캘린더 i디스턴스 K-ary 좌측자녀 우측자매 링크/컷 로그 구조화 결합 머클 p q. 범위 SPQR 정상

Search

k-d 트리

네임스페이스

더

목차

묘사

k-d 트리에 대한 작업

건설

구현 예시

요소 추가

요소 제거

밸런스

가장 가까운 네이버 검색

범위 검색

고차원 데이터에 의한 성능 저하

쿼리 포인트가 k-d 트리의 포인트와 멀리 떨어져 있는 경우 성능 저하

복잡성

바리에이션

볼륨 측정 객체

잎만 포인트

「」를 참조해 주세요.

오픈 소스 구현

레퍼런스

Search

k-d 트리

묘사

k-d 트리에 대한 작업

건설

구현 예시

요소 추가

요소 제거

밸런스

가장 가까운 네이버 검색

범위 검색

고차원 데이터에 의한 성능 저하

쿼리 포인트가 k-d 트리의 포인트와 멀리 떨어져 있는 경우 성능 저하

복잡성

바리에이션

볼륨 측정 객체

잎만 포인트

「 」를 참조해 주세요.

오픈 소스 구현

레퍼런스

「」를 참조해 주세요.