트리 회전
Tree rotation이산 수학에서 트리 회전은 요소의 순서를 방해하지 않고 구조를 바꾸는 이진수 트리의 연산입니다.트리 회전은 트리 내에서 한 노드를 위쪽으로, 한 노드를 아래로 이동합니다.트리의 모양을 변경하는 데 사용되며, 특히 작은 서브트리를 아래로, 큰 서브트리를 위로 이동함으로써 높이를 낮추기 위해 사용되며, 결과적으로 많은 트리 작업의 성능이 향상됩니다.
회전 방향의 정의에 대한 여러 설명에 일관성이 없습니다.어떤 이들은 회전 방향이 노드가 회전할 때 움직이는 방향을 반영한다고 말하는 반면, 다른 이들은 회전 방향이 어떤 서브트리가 회전하고 있는지를 반영한다고 말한다(왼쪽 서브트리가 부모 위치로 회전하는 것은 형태와 반대되는 왼쪽 서브트리가 회전 방향은 어떤 서브트리를 반영한다고 말한다.er) 이 글은 회전 노드의 방향 이동에 접근한다.
일러스트
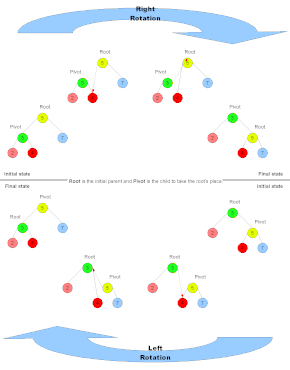
인접 이미지에 나타난 것과 같은 오른쪽 회전 조작은 Q를 루트로 하여 수행되므로 Q에 대해 오른쪽 회전 또는 루트를 합니다.이 작업을 수행하면 트리가 시계 방향으로 회전합니다.역작전은 왼쪽 회전으로, 반시계 방향으로 이동하게 됩니다(위의 왼쪽 회전은 P에 뿌리를 두고 있습니다).회전의 기능을 이해하기 위한 열쇠는 회전의 제약을 이해하는 것입니다.특히 트리의 잎 순서(예를 들어 왼쪽에서 오른쪽으로 읽었을 때)는 변경할 수 없습니다(순서대로 트래버설로 잎을 방문하는 순서는 이전과 동일해야 합니다).또 다른 제약사항은 이진 검색 트리의 주요 속성입니다. 즉, 오른쪽 하위가 부모보다 크고 왼쪽 하위가 부모보다 작습니다.서브트리의 루트의 왼쪽 자녀(예를 들어 Q에 루트된 트리의 그림에서 노드B)의 오른쪽 자녀는 루트의 왼쪽 자녀가 될 수 있으며, 그 자체가 회전된 서브트리의 "새로운" 루트의 오른쪽 자녀가 될 수 있습니다.그림에서 보듯이 잎의 순서는 변하지 않습니다.반대쪽 동작도 순서를 유지하며 두 번째 종류의 회전입니다.
위에서 설명한 바와 같이 이것이 이진 검색 트리라고 가정하면 요소는 서로 비교할 수 있는 변수로 해석되어야 합니다.왼쪽의 알파벳 문자는 이러한 변수의 자리 표시자로 사용됩니다.오른쪽 애니메이션에서는 대문자 알파벳이 변수 자리 표시자로 사용되고 그리스 소문자가 변수 집합 전체에 대한 자리 표시자로 사용됩니다.원은 개별 노드를 나타내고 삼각형은 하위 트리를 나타냅니다.각 서브트리는 비어 있거나 단일 노드로 구성되거나 임의의 수의 노드로 구성될 수 있습니다.
상세 일러스트
서브트리가 회전할 때 서브트리가 회전하는 서브트리 측은 그 높이를 한쪽 노드만 증가시키고 다른 쪽 서브트리는 그 높이를 감소시킵니다.이를 통해 트리 회전이 트리의 균형을 재조정하는 데 유용합니다.
회전하는 서브트리의 부모 노드에는 루트, 새로운 부모 노드가 되는 노드에는 피벗, 회전하는 쪽에는 RS, 회전하는 쪽에는 OS라는 용어를 검토합니다.위 그림의 루트Q는 RS는 C, OS는 P입니다.이러한 용어를 사용하여 회전의 의사 코드는 다음과 같습니다.
피벗 = 루트입니다.OS 루트OS = 피벗.RS 피벗RS = 루트 루트 = 피벗
이것은 고정 시간 작업입니다.
또한 프로그래머는 루트의 부모가 회전 후 피벗을 가리키는지 확인해야 합니다.또한, 프로그래머는 이 조작으로 인해 트리 전체에 새로운 루트가 발생할 수 있다는 점에 유의하고 그에 따라 포인터를 업데이트해야 합니다.
순서 불변성
트리 회전에 의해 바이너리 트리의 순서는 불변합니다.이는 트리의 모든 부분에서 회전이 수행될 때 요소의 순서가 영향을 받지 않음을 의미합니다.위에 나타낸 트리의 순서대로 트래버스를 다음에 나타냅니다.
왼쪽 트리: (A, P, B), Q, C) 오른쪽 트리: (A, P, (B, Q, C)
하나를 다른 것으로부터 계산하는 것은 매우 간단합니다.다음은 해당 계산을 수행하는 Python 코드의 예입니다.
방어하다 right_filename(오른쪽)(삼면체): "지정된 트리를 오른쪽으로 회전시킵니다.""" 왼쪽, Q, C = 삼면체 A, P, B = 왼쪽 돌아가다 (A, P, (B, Q, C)) 또 다른 시각은 다음과 같습니다.
노드 Q의 오른쪽 회전:
P를 Q의 왼쪽 아이로 두자.Q의 왼쪽 아이를 P의 오른쪽 아이로 설정합니다.[P의 오른쪽 자녀 부모를 Q로 설정]P의 오른쪽 자녀 부모를 Q로 설정합니다.[Q의 부모를 P로 설정]
노드 P의 왼쪽 회전:
Q를 P의 올바른 아이로 만들자.P의 오른쪽 아이를 Q의 왼쪽 아이로 설정합니다.[Q의 왼쪽 자녀 부모를 P로 설정]Q의 왼쪽 자녀 부모를 P로 설정][P의 부모를 Q로 설정]
다른 모든 연결은 현재 상태로 유지됩니다.
좌우 회전의 조합인 이중 회전도 있습니다.X에서의 이중좌회전이란 X의 우측자녀에서 우회전, X에서의 좌측자녀에서 좌회전, X에서의 이중좌회전, X에서의 우측자녀의 좌측자녀에서 좌회전, X에서의 우측자녀에서 우회전 순으로 정의할 수 있다.
트리 로테이션은 AVL 트리, 레드-블랙 트리, WAVL 트리, 스플레이 트리 및 트리프 등 다양한 트리 데이터 구조에 사용됩니다.로컬 변환이므로 일정 시간만 필요합니다. 5개의 노드에서만 작동하며 트리의 나머지 부분을 검사할 필요가 없습니다.
재밸런싱을 위한 회전
트리는 회전을 사용하여 균형을 재조정할 수 있습니다.회전 후 회전측도 높이가 1 증가하는 반면 회전측도 마찬가지로 높이가 감소합니다.따라서 왼쪽 아이와 오른쪽 아이의 키가 1개 이상 차이가 나는 노드에 전략적으로 회전을 적용할 수 있다.자체 밸런싱 바이너리 검색 트리는 이 작업을 자동으로 적용합니다.이 재조정 기술을 사용하는 트리의 종류는 AVL 트리입니다.
회전 거리
노드 수가 같은 2개의 바이너리 트리 간의 회전 거리는 한 개를 다른 것으로 변환하는 데 필요한 최소 회전 수입니다.이 거리에서 n-노드 이진 트리 집합은 메트릭 공간이 된다. 즉, 거리는 대칭이며, 두 개의 다른 트리가 주어졌을 때 양수이며 삼각 부등식을 만족한다.
회전 거리를 계산하기 위한 다항식 시간 알고리즘이 존재하는지 여부는 미해결 문제이다.그러나, Fordham의 알고리즘은 선형 시간으로 거리를 계산하지만, (ab)c = a(bc)와 a(bc)d = a(bc)의 두 가지 종류의 회전만 허용합니다.Fordham 알고리즘은 노드를 7가지 유형으로 분류하는 데 의존하며, 룩업 테이블을 사용하여 한 유형의 노드를 다른 노드로 변환하는 데 필요한 회전 수를 구합니다.
다니엘 슬레이터, 로버트 타잔, 윌리엄 서스턴은 두 개의 n-노드 나무 사이의 회전 거리(n ≤ 11)가 최대 2n - 6이며, n이 충분히 [1]크면 일부 쌍이 이만큼 떨어져 있음을 보여주었다.라이오넬 푸르닌은 사실 11번과 11번 [2]모두 그러한 쌍이 존재한다는 것을 보여주었다.
「 」를 참조해 주세요.
- AVL 트리, 빨간색-검은색 트리 및 스플레이 트리, 회전을 사용하여 균형을 유지하는 바이너리 검색 트리 데이터 구조의 일종입니다.
- 이진 연산의 연관성은 이 연산에서 트리 회전을 수행해도 최종 결과는 변경되지 않음을 의미합니다.
- Day-Stout-Warren 알고리즘은 불균형 BST의 균형을 조정합니다.
- Tamari 격자는 요소가 이진 트리로 정의될 수 있고 요소 간의 순서가 트리 회전에 의해 정의되는 부분 순서 집합입니다.
레퍼런스
- ^ 를 클릭합니다Sleator, Daniel D.; Tarjan, Robert E.; Thurston, William P. (1988), "Rotation distance, triangulations, and hyperbolic geometry", Journal of the American Mathematical Society, 1 (3): 647–681, doi:10.2307/1990951, JSTOR 1990951, MR 0928904.
- ^ 를 클릭합니다Pournin, Lionel (2014), "The diameter of associahedra", Advances in Mathematics, 259: 13–42, arXiv:1207.6296, doi:10.1016/j.aim.2014.02.035, MR 3197650.