유클리드 최소 신장 트리

유클리드 평면 또는 고차원 유클리드 공간의 유한 집합의 유클리드 최소 신장 트리는 점을 끝점으로 하는 선분 체계로 점을 연결하여 세그먼트의 전체 길이를 최소화합니다.그 안에서 임의의 두 점은 선분을 통과하는 경로를 따라 서로 도달할 수 있습니다.점을 정점으로 하고 점 사이의 유클리드 거리를 에지 가중치로 하는 완전한 그래프의 최소 신장 트리로 찾을 수 있습니다.

최소 신장 트리의 가장자리는 정점에 대해 최소 60°, 최대 6°의 각도로 만납니다.고차원에서 정점당 모서리 수는 접선 단위 구의 키싱 수에 의해 제한됩니다.단위 제곱의 점에 대한 모서리의 총 길이는 점 개수의 제곱근에 최대 비례합니다.각 가장자리는 평면의 빈 영역에 놓여 있으며, 이 영역은 유클리드 최소 신장 트리가 상대 이웃 그래프 및 들라우네 삼각 분할을 포함한 다른 기하 그래프의 하위 그래프임을 증명하는 데 사용될 수 있습니다.Delaunay 삼각 분할을 구성한 다음 그래프 최소 신장 트리 알고리즘을 적용하여 평면 점이 $주어진$ n ${\displaystyle n}$의 최소 신장 트리를 시간 O${\displaystyle (\mathrm{nlog}}$ ⁡ n$){\displaystyle O(n\log n)}$에서 찾을 수 있습니다$.$이것은 일부 계산 모델에서 최적이지만, 정수 좌표를 가진 점에 대해서는 더 빠른 무작위 알고리즘이 존재합니다.고차원의 점의 경우 최적의 알고리즘을 찾는 것은 여전히 미해결 문제로 남아 있습니다.

정의 및 관련 문제

유클리드 평면 또는 유클리드 공간에 $있는{\displaystyle }$ n개의 ${\displaystyle n}$개의$$ 점 집합에 대한 유클리드 최소 신장 트리는 주어진 점만 끝점으로 가지는 선분의 체계이며, 그 결합은 연결된 집합의 모든 점을 포함하고 이러한 시스템의 가능한 총 길이가 최소입니다.이러한 네트워크는 세그먼트의 다각형 링을 포함할 수 없습니다. 세그먼트가 존재하는 경우 다각형의 가장자리를 제거하여 네트워크를 단축할 수 있습니다.따라서 최소 길이 네트워크는 트리를 형성합니다.이러한 관측은 유클리드 최소 신장 트리가 최소 총 길이의 주어진 점 쌍 사이의 선분 트리라는 동등한 정의로 이어집니다.^[1]동일한 트리를 가중치가 부여된 완전 그래프의 최소 신장 트리로 설명할 수도 있으며, 주어진 점을 정점으로 하고 점 사이의 거리를 에지 가중치로 합니다.^[2]동일한 점에 두 개 이상의 최소 신장 트리가 있을 수 있습니다.예를 들어, 일반 다각형의 꼭짓점의 경우, 다각형의 가장자리를 제거하면 최소 신장 트리가 생성됩니다.^[3]

유클리드 최소 신장 트리에 대한 출판물은 일반적으로 "EMST"로 약칭합니다.^[4][5]"기하학적 최소 신장 트리"라고도 할 수 있지만,^[6][7] 이 용어는 L 공간과 같이^p 비유클리드 거리가 있는 기하학적 공간에 더 일반적으로 사용될 수 있습니다.^[8]유클리드 점 집합의 문맥이 명확할 때, 그것들은 단순히 "최소 신장 트리"라고 불릴 수 있습니다.^[9][10][11]

다른 여러 표준 기하학 네트워크는 유클리드 최소 신장 트리와 밀접한 관련이 있습니다.

• 슈타이너 트리 문제는 주어진 점에서만 시작과 종료를 요구하지 않고 모든 주어진 점을 연결하는 선분 시스템을 다시 찾습니다.이 문제에서는 세그먼트 끝점으로 추가 지점이 추가되어 스타이너 트리가 최소 신장 트리보다 짧을 수 있습니다.^[12]
• 유클리드 순회 판매원 경로 문제에서 연결선 세그먼트는 스패닝 트리와 같이 주어진 점에서 시작하고 종료해야 하며 슈타이너 트리와는 달리 각 점은 최대 두 개의 선 세그먼트에 접촉할 수 있으므로 결과는 다각형 체인을 형성합니다.이러한 제한 때문에 최적 경로는 유클리드 최소 신장 트리보다 길 수 있지만 최대 두 배입니다.^[2]
• 기하학적 스패너는 최소 신장 트리처럼 모든 점을 연결하는 저중량 네트워크입니다.최소 신장 트리와는 달리, 이러한 모든 연결 경로는 연결 지점 간의 거리에 비례하는 길이를 갖도록 요구됩니다.이 속성을 달성하기 위해 이러한 네트워크는 일반적으로 주기를 가지며 트리가 아닙니다.^[13]

특성.

각도 및 꼭지점 도

유클리드 최소 신장 트리의 두 모서리가 꼭지점에서 만날 때마다 60° 이상의 각도를 형성해야 하며, 정삼각형의 두 변을 형성할 때만 동일합니다.이는 더 날카로운 각도를 형성하는 두 모서리의 경우 두 모서리 중 하나가 삼각형의 세 번째 짧은 모서리로 대체되어 전체 길이가 더 작은 트리를 형성할 수 있기 때문입니다.^[14]이에 비해 슈타이너 트리 문제는 각도 경계가 더 강합니다. 최적의 슈타이너 트리는 모든 각도가 최소 120°^[12]입니다.

유클리드 공간에서 두 개의 구가 교차하지 않고(접선점을 넘어) 중심 단위 구에 접할 수 있는 최대 단위 구를 찾는 키싱 수 문제에서도 동일한 60° 각도 경계가 발생합니다.이 구들의 중심점은 별 형태의 최소 신장 트리를 가지며, 중심점은 다른 모든 점에 인접합니다.반대로, 최소 신장 트리의 모든$$ 정점 $v{\displaystyle }$ ${\displaystyle v}$에 대해 $v{\displaystyle }$ ${\displaystyle v}$ 및 각$$ 가장자리를 따라 두 개의 점에 v ${\displaystyle v}$의 각 이웃에 대한 접선을 사용하여 중첩되지 않는 단위 구를 구성할 수 있습니다$.$따라서 $n개$의$${\$displaystyle n}$차원 공간에서$$ 정점의 최대 가능한 정도(연결된 신장 트리 가장자리의 수)는$n개$의 {\displaystyle $n}$차원에서$$ 키싱 구의 수와 같습니다.^[15]평면 최소 신장 트리는 최대 6도를 가지며, 트리가 6도를 가질 때 항상 최대 5도를 가지는 다른 최소 신장 트리가 있습니다.^[7]3차원 최소 신장 트리는 최대 12개의 각도를 갖습니다.^[15]키스 숫자의 정확한 값이 알려진 더 높은 차원은 4차원, 8차원, 그리고 24차원뿐입니다.^[16]

주어진 연속 분포에서 임의로 생성된 점의 경우 최소 신장 트리는 거의 유일합니다.주어진 차수의 정점 수는 많은 수의 정점에 대해 그 정점 수의 일정한 배로 수렴합니다.이러한 상수의 값은 정도와 분포에 따라 달라집니다.그러나 단위 제곱에 균일하게 분포된 점의 잎 수와 같은 단순한 경우에도 정확한 값을 알 수 없습니다.^[17]

빈 지역

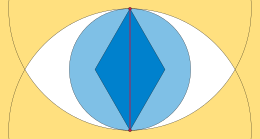
유클리드 최소 신장 트리의$$ 임의의 ${\displaystyle \mathrm{edge}}$ u$$v {\$displaystyle$uv}에 대해, ${\displaystyle \mathrm{uv}}$ ${\displaystyle uv}$를 반경으로$$ 하여 두 원을 교차시켜 형성된 렌즈(또는 베시카 피스시스)는 내부에 다른$$ 주어진 정점 $w{\displaystyle }$ ${\displaystyle w}$을 가질 수 없습니다.다른 방법으로, 렌즈가 세 번째 $점{\displaystyle }$ w ${\displaystyle$ w$}$을(를) 포함하는$$ 에지 ${\displaystyle u}$ v ${\displaystyle uv}$이(가) 있는 트리의 경우 최소 길이가 아닙니다$.$두 원의 기하학적 $구조$에$$따라 w {\$displaystyle w}$는$u$ {\$displaystyle$ $u$}$$및 v {\$displaystyle v}$ 둘 다에 가깝습니다$$$$.Edge $u{\displaystyle }$ ${\displaystyle v}$ ${\displaystyle$ u$}$이(가) 트리에서 제거된$$ 경우 $w{\displaystyle }$ ${\displaystyle$ w}은$($는) u ${\displaystyle u}$ $및$ v ${\displaystyle v}$ 중 하나에 연결된 상태로 유지되지만$$ 다른 하나는 연결되지 않습니다$.$제거된 Edge $u{\displaystyle }$ ${\displaystyle v}$ ${\displaystyle uv}$을(를) $u{\displaystyle }$ ${\displaystyle uw}$ 또는$$ ${\displaystyle \mathrm{vw}}$ ${\displaystyle vw}($연결이 끊긴 $정점$에 w\$displaystyle w}$을(를) 다시 연결하는 두 에지 중 하나)$$로 대체하면 더 짧은 트리가 생성됩니다.^[12]

유클리드 최소 신장 트리의 가장자리$$ $u{\displaystyle }$ ${\displaystyle v}$ ${\$$displaystyle uv}$에 대해, $u{\displaystyle }$ v {\${\displaystyle \mathrm{displaystyle}}$ $uv}$를 긴$$대각선으로 하는$$ 60° 및 120° 각도의 마름모는 다른 모든 가장자리에 의해 유사하게 형성된 마름모와 서로소입니다.끝점을 공유하는 두 모서리는 중첩된 마름모를 가질 수 없는데, 이는 60°보다 더 날카로운 모서리를 의미하고, 두 개의 서로소인 모서리는 중첩된 마름모를 가질 수 없기 때문입니다. 두 모서리 중 더 긴 모서리는 동일한 네 개의 꼭짓점 사이에서 더 짧은 모서리로 대체될 수 있습니다.^[12]

수퍼그래프

특정 기하 그래프에는 점 집합의 빈 영역을 포함하는 정의가 있으며, 이 정의에서 유클리드 최소 신장 트리의 일부가 될 수 있는 모든 가장자리를 포함합니다.여기에는 다음이 포함됩니다.

• 상대 인접 그래프는 정의된 렌즈가 비어 있을 때마다 점 쌍 사이에 가장자리가 있습니다.
• 쌍을 지름으로 하는 원이 비어 있을 때마다 점 쌍 사이에 가장자리가 있는 가브리엘 그래프.
• 한 쌍을 코드로 갖는 빈 원이 존재할 때마다 점 쌍 사이에 가장자리가 있는 들라우네 삼각형.
• 각 삼각형의 가장 긴 모서리를 제거하여 들라우네 삼각형에서 형성된 우르쿠하트 그래프입니다.나머지 각 모서리에 대해 해당 모서리를 사용하는 들라우네 삼각형의 꼭짓점은 상대 인접 그래프의 빈 달에 놓일 수 없습니다.

이러한 그래프의 빈 영역 기준이 점진적으로 약하기 때문에 이러한 그래프는 순서가 있는 하위 그래프 시퀀스를 형성합니다.즉, ⊆를 사용하여 가장자리 사이의 부분집합 관계를 나타내면 다음과 같은 관계를 갖습니다.

최소 신장 트리를 포함하도록 보장된 또 다른 그래프는 야오 그래프로, 각 점 주위의 평면을 6개의 60° 웨지로 나누고 각 점을 각 웨지에서 가장 가까운 이웃과 연결하여 평면의 점에 대해 결정됩니다.결과 그래프에는 상대 이웃 그래프가 포함되는데, 빈 렌즈를 가진 두 꼭지점은 쐐기에서 서로 가장 가까운 이웃이어야 하기 때문입니다.위의 다른 많은 기하학 그래프와 마찬가지로, 이 정의는 더 높은 차원으로 일반화될 수 있으며, 들라우네 삼각형과는 달리 일반화는 항상 선형 수의 에지를 포함합니다.^[20][21]

총길이

단위 사각형에 있는 $n개$의 ${\displaystyle n}$개의$$ 점(또는 기타 고정된 모양)에 대해 최소 신장 트리 가장자리의 총 길이는 $O{\displaystyle (n)}$ ${\displaystyle$ O$({\sqrt {n})}$입니다${\displaystyle .}$xn ${\${\$sqrt {n}}$개$$ 격자에 균등하게 위치한 점 등 일부 점 집합이 이 경계에 도달합니다.^[12]$단위{\displaystyle }$ 하이퍼큐브가 {\$displaystyle d}$차원$$ 공간에 있는 점의 경우 해당 경계는 $O{\displaystyle ({}^{(d}}$ -${\displaystyle 1^{}}$)${\displaystyle {}^{}}$/ ${\displaystyle d^{}}$ ${\displaystyle O(n^{(d-1)/d})}$입니다$.$^[22]단위 사각형 또는 단위 하이퍼큐브에서 균일하고 독립적으로 선택된 $n개$의 ${\displaystyle n}$개$$ 점에 대한 최소 신장 트리의 예상 총 길이에 동일한 경계가 적용됩니다.^[23]단위 제곱으로 돌아가면 최소 신장 트리의 모서리 길이 제곱의 합은 $O{\displaystyle (1)}$ ${\displaystyle O(1)}$입니다$.$이 경계는 가장자리에 서로소 마름모가 있고 가장자리 길이 제곱에 비례하는 면적이 있다는 관측 결과를 따릅니다.전체 길이에서 $O{\displaystyle (n)}$ ${\displaystyle O({\sqrt {n}})}$ 경계는$$ 코시-슈바르츠 부등식을 적용하여 이어집니다.^[12]

이 결과에 대한 또 다른 해석은 단위 사각형의 점 집합에 대한 평균 모서리 길이가 $O{\displaystyle (1\sqrt{}}$/ n${\displaystyle }$) ${\displaystyle O(1$ / ${\sqrt {n}})}$이며$,$ 정규 격자의 점 간격에 최대 비례한다는 것입니다. 그리고 단위 사각형의 임의의 점에 대한 평균 $길이$는${\displaystyle }$1 / ${\displaystyle n\sqrt{}}$ ${\$1 / ${\sqrt {n}}$에 비례한다는 것입니다$.$ 어떻게ver, 확률이 높은 경우 가장 긴 모서리의 길이는 대략적으로

비 constant 계수에 의한 평균보다 긴 값입니다.높은 확률로 가장 긴 에지는 신장 트리의 리프를 형성하고 다른 모든 점으로부터 멀리 떨어진 점을 가장 가까운 이웃에 연결합니다.많은 수의 점의 경우 기대 값을 중심으로 가장 긴 모서리 길이의 분포가 라플라스 분포로 수렴됩니다.^[24]

유클리드 거리에 가까운 최단 경로를 갖는 완전한 기하학 그래프의 하위 그래프인 기하학적 스패너는 적어도 최소 스패닝 트리만큼 큰 총 모서리 길이를 가져야 합니다.기하학적 스패너에 대한 표준 품질 척도 중 하나는 같은 점에 대한 총 길이와 최소 스패너 트리 사이의 비율입니다.탐욕스러운 기하학적 스패너와 같은 스패너를 구성하는 여러 방법은 이 비율에 대한 일정한 경계를 달성합니다.^[13]평면의 동일한 점 집합에 대해 최소 신장 트리의 총 길이와 슈타이너 트리 사이의 가능한 최대 비율인 슈타이너 비율은 $2{\displaystyle /3}$ ≈ ${\displaystyle 1.1547}$ ${\displaystyle 2/{\sqrt {3}}\약 1.1547}$로$$정삼각형의 세 점에 대한 비율이라고 추측되었습니다.

세분류

유클리드 최소 신장 트리의 모든 가장자리가 그 중점에 새로운 점을 추가하여 세분화된 경우, 결과 트리는 여전히 증강 점 집합의 최소 신장 트리입니다.이 세분화 과정을 반복하면 유클리드 최소 신장 트리가 임의로 미세하게 세분화될 수 있습니다.그러나 일부 가장자리만 세분화하거나 중간점이 아닌 점에서 가장자리를 세분화하면 세분화된 트리가 최소 신장 트리가 아닌 점 집합이 생성될 수 있습니다.^[25]

계산 복잡도

어떤 차원의 점에 대해서도, 최소 신장 트리는 유클리드 거리로 가중치를 부여하여 모든 점 쌍 사이의 가장자리를 갖는 완전한 그래프를 구성함으로써$$ $시간{\displaystyle }$ O ${\displaystyle ({}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle O(n^{2})}$에 구성할 수 있습니다.그리고 나서 Prim-Dijkstra-Jarnik 알고리즘 또는 Bor ůvka 알고리즘과 같은 그래프 최소 신장 트리 알고리즘을 적용합니다.이 알고리즘은 다른 일반적인 선택인 Kruskal의 알고리즘과 달리 완전한 그래프에서 시간$$ $O{\displaystyle }$(${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$) ${\displaystyle O(n^{2})}$이(가) 걸리도록 만들 수 있는데, 이는 모든 거리를 정렬하는 것을 포함하기 때문에 더 느립니다.^[13]저차원 공간에 있는 점의 경우 아래에서 자세히 설명하는 것처럼 문제를 더 빨리 해결할 수 있습니다.

유클리드 거리 계산에는 제곱근 계산이 포함됩니다.에지 가중치를 비교할 때 거리 자체 대신 유클리드 거리의 제곱을 비교하면 동일한 순서가 산출되므로 트리의 나머지 계산은 변경되지 않습니다.이 바로 가기를 사용하면 계산 속도가 빨라지고 정수 산술만 사용하여 좌표가 정수인 점에 대한 최소 신장 트리를 구성할 수 있습니다.^[20]

2차원

평면 점의 최소 신장 트리를 찾는 더 빠른 접근법은 들라우네 삼각형의 하위 그래프라는 속성을 사용합니다.

1. Delaunay 삼각측량을 계산합니다$.$ 이는 O($nlog$ ⁡ ${\displaystyle n}$) $displaystyle O(n\log$ n$)} 시간$ 내에 수행할 수 있습니다.들라우네 삼각형은 평면 그래프이므로 최대 ${\displaystyle \mathrm{3n}}$ -${\displaystyle 6}$ ${\displaystyle 3n$ - 6$}$개의 모서리를 가집니다$$.
2. 각 모서리에 (제곱) 길이로 레이블을 지정합니다.
3. 그래프 최소 신장 트리 알고리즘을 실행합니다.$O{\displaystyle (n)}$ ${\displaystyle O(n)}$개의 에지가 있으므로 표준 최소 신장 트리 알고리즘을 사용하여 $O{\displaystyle (\mathrm{nlog}}$ ⁡ ${\displaystyle n)}$ ${\displaystyle O(n\log n)}$시간이 필요합니다.

결과적으로 $O{\displaystyle }$(${\displaystyle n}$ log ⁡ ${\displaystyle n}$) ${\displaystyle O(n\log n)}$ 시간이 걸리는 알고리즘이며, 특정 계산 모델에서 최적입니다(아래 참조).

입력 좌표가 정수이고 배열 인덱스로 사용할 수 있다면 더 빠른 알고리즘이 가능합니다. 들라우네 삼각형은 O (${\displaystyle n\log }$ ⁡ ${\displaystyle \log }$ ⁡ ${\displaystyle n)}$ ${\displaystyle O(n\log \log n)}$ 예상 시간에서 무작위 알고리즘으로 구성할 수 있습니다.또한 들라우네 삼각형은 평면 그래프이기 때문에 최소 신장 트리는 알고리즘의 각 단계 후 각 구성 요소 쌍 사이의 가장 저렴한 에지를 제외한 모든 것을 제거하는 Bor ůvka 알고리즘의 변형에 의해 선형 시간으로 찾을 수 있습니다.따라서 이 알고리즘의 총 예상 시간은 $O{\displaystyle (n}$ ${\displaystyle \log }$ ⁡ ${\displaystyle \log }$ ⁡ ${\displaystyle n)}$ ${\displaystyle O(n\log \log n)}$입니다$.$ 다른 방향으로는 Delaunay 삼각형을 선형 시간 경계 $O{\displaystyle (n}$ ${\displaystyle {\log }^{}}$ ∗ ⁡ ${\displaystyle n)}$ ${\displaystyle O(n\log ^{*}n)}$의 최소 신장 트리로 구성할 수 있습니다$.$여기서 ${\displaystyle {\log }^{}}$ ∗ ${\displaystyle \log ^{*}$는 반복 로그를 나타냅니다.

고차원

이 문제는 $또한{\displaystyle }$ d ${\displaystyle$ d$}$ - 차원$$ $공간{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}${\$displaystyle {R}$^{$d}$의 n$${\$displaystyle n}$ 점으로 일반화될 수 있습니다$.$ 고차원에서 들라우네 삼각 분할(Delaunay triangulation, 마찬가지로 볼록 선체를 $d{\displaystyle }$ ${\displaystyle d}$ - 차원$$ 단순으로 분할)에 의해 결정된 연결은 최소 스팬을 포함합니다.ning tree; 그러나 삼각측량은 완전한 그래프를 포함할 수 있습니다.^[4]따라서 유클리드 최소 신장 트리를 완전 그래프의 신장 트리 또는 들라우네 삼각형의 신장 트리로 찾는 것은 모두 $O{\displaystyle }$(${\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle O(dn^{2})}$시간이$$ 걸립니다.3차원의 경우 최소 신장 트리는 O $시간{\displaystyle ((\mathrm{nlog}}$⁡${\displaystyle {}^{}n}$ ) ${\displaystyle 4^{}}$/ 3${\displaystyle {}^{}}$)$${\$displaystyle O{\bigl (}(n\log$ n$)^{4/3}{\bigr )}},$ 그리고$$더 큰 차원에서 시간 내에 찾을 수 있습니다.

의ε >0 {\$displaystyle$ \$varepsilon$ >$0}$- 완전 그래프 및 들라우네 삼각 분할 알고리즘에 대한 2차 시간 경계보다 빠릅니다.

고차원 최소 신장 트리에 대한 최적의 시간 복잡성은 알려지지 않았지만,^[29] 이중 색 근접 쌍 계산의 복잡성과 밀접한 관련이 있습니다.쌍채색 최인접 쌍 문제에서 입력은 두 가지 다른 색(예를 들어, 빨간색과 파란색)이 주어진 점의 집합입니다.출력은 가능한 거리가 최소인 빨간색 점과 파란색 점의 쌍입니다.이 쌍은 항상 최소 신장 트리의 가장자리 중 하나를 형성합니다.따라서, 쌍채색으로 가장 가까운 쌍 문제는 최소 신장 트리를 구성하고 가장 짧은 적색-청색 에지를 위해 가장자리를 스캔하는 데 걸리는 시간으로 해결할 수 있습니다.반대로, 주어진 점 집합의 모든 부분 집합의 모든 빨강-파랑 색상에 대해, 쌍채색으로 가장 가까운 쌍은 부분 집합의 최소 신장 트리의 한 가장자리를 생성합니다.하위 집합의 일련의 색칠을 신중하게 선택하고 각 하위 문제의 이중색 가장 가까운 쌍을 찾음으로써, 최적의 시간이 무엇이든 동일한 수의 점에 대한 이중색 가장 가까운 쌍을 찾는 최적의 시간에 비례하는 최소 신장 트리를 찾을 수 있습니다.^[4][11]

임의의 경계 차원에서 균일하게 랜덤한 점 집합의 경우 Yao 그래프^[20] 또는 Delaunay 삼각형은 선형 예상 수의 에지를 가지며 최소 신장 트리를 포함하도록 보장되며 선형 예상 시간으로 구성할 수 있습니다.^[21][6][30]이러한 그래프에서 최소 신장 트리 자체는 그래프 최소 신장 트리에 대해 무작위화된 선형 시간 알고리즘을 사용하여 선형 시간으로 구성될 수 있습니다.^[31]그러나 클러스터링된 데이터에서 오는 입력에 대한 이러한 방법의 성능이 좋지 않아 알고리즘 공학 연구자들은 거리와 클러스터링이 랜덤 데이터와 유사한 랜덤 입력 또는 입력에 대해 O(${\displaystyle n}log$ ⁡ $){\displaystyle O(n\log n)}$ 시간 경계가 다소 느린 방법을 개발하게 되었습니다.실제 데이터에서 더 나은 성능을 발휘할 수 있습니다.^[8][32][5]

잘 분리된 쌍 분해는 주어진 점들의 부분집합 쌍들의 집합으로, 모든 점들의 쌍들이 이러한 부분집합 쌍들 중 하나에 속하며, 동일한 부분집합 쌍에서 나오는 모든 점들의 쌍들이 거의 동일한 길이를 갖도록 합니다.선형 수의 부분 집합을 갖는 잘 분리된 쌍 분해와 각 부분 집합에 대한 대표적인 점 쌍을 시간 $O{\displaystyle (n}$ ${\displaystyle \log }$ ⁡ ${\displaystyle n)}$ ${\displaystyle O(n\log n)}$에서 찾을 수 있습니다$.$이러한 대표 쌍으로 구성된 그래프의 최소 신장 트리는 최소 신장 트리에 대한 근사치입니다.이러한 아이디어를 사용하면$,$ (${\displaystyle 1}$ +${\displaystyle }$ε${\displaystyle )}$ ${\displaystyle (1+\$$varepsilon$ $)}$ - 최소 신장 트리에 근접한 값을 $O$ ${\displaystyle (n}$ ${\displaystyle \log }$ ⁡ ${\displaystyle n)}$ ${\displaystyle$$O(n\log$ n$)}$ 시간 내에 찾을 수 있습니다$.$ 보다 정확하게는, 동치 클래스에서 가장 가까운 쌍을 근사화할 각 대표 쌍을 선택하고 신중하게 변경합니다.서로 다른 쌍에 대한 이 근사치의 품질에 대해, 시간 경계에서 ε ${\displaystyle \varepsilon}$에 대한 의존성은 O($n$ ${\displaystyle \mathrm{로그}}$ ⁡ ${\displaystyle n}$ + (${\displaystyle }$ε -${\displaystyle {}^{}}$2 ${\displaystyle {\mathrm{로그}}^{}}$ ${\displaystyle 2^{}}$ ⁡ ${\displaystyle 1}$ ε${\displaystyle }$) ${\displaystyle n}$ ${\displaystyle ),}$ 고정 차원에 대해 ${\displaystyle O(n\log n+(\varepsilon ^{-2})\log ^{2}{\tfrac {1}{\varepsilon })n})$로 지정할 수 있습니다.

동적 및 동적

유클리드 최소 신장 트리는 다양한 방법으로 이동하거나 점을 변경하는 시스템으로 일반화되었습니다.

• 점 집합이 일련의 동적 삽입 또는 점 삭제를 겪는 경우, 이러한 업데이트 각각은 점의 최소 신장 트리에 제한된 양의 변경을 유도합니다.평면의 점에 대해 업데이트 순서를 미리 알 수 있는 경우 각 삽입 또는 삭제 후의 변경 사항은 삽입 또는 삭제 시 O $시간{\displaystyle ({\log }^{}}$ ${\displaystyle 2^{}}$ ⁡ ${\displaystyle n}$) ${\displaystyle O(\log ^{2}n)}$에 확인할 수 있습니다.업데이트를 온라인 방식으로 처리해야 하는 경우 더 느린(그러나 여전히 다논리식) $O{\displaystyle ({\log }^{}}$ ${\displaystyle {10}^{}}$ ⁡${\displaystyle n)}$ ${\displaystyle O(\log ^{10}n)}$ 시간 바인딩을 알 수 있습니다.문제의 고차원 버전의 경우 업데이트당 시간은 느리지만 여전히 하위 선형입니다.^[36]
• 일정한 속도로 선형으로 이동하는 $n개$의 ${\displaystyle n}$개의$$ 점 또는 더 일반적인 대수적 움직임의 경우, 최소 신장 트리는 한 에지가 제거되고 다른 에지가 길이가 같은 시점에 대체되는 일련의 스왑에 의해 변경됩니다.^[37]선형 운동의 경우, 변화의 수는 기껏해야 n ${\displaystyle {25\mathrm{}}^{}}$/ 9 ${\$보다 약간 큽니다$.$^[38] 보다 일반적인 대수 운동의 경우, 대븐포트-신젤 수열 이론에 기초하여 스왑 횟수에 대한 입방체에 가까운 상한이 있습니다.^[39]
• 최소 이동 스패닝 트리 문제는 다시 일정한 속도로 일정한 간격으로 선형적으로 이동하는 점에 관한 것으로, 이 간격 동안 발생하는 가중치의 최대 합을 최소화하는 단일 트리를 찾습니다.정확하게 계산하는 것은 NP-hard이지만 다항 시간 내에 2배 이내로 근사할 수 있습니다.^[40]
• 운동 유클리드 최소 신장 트리 문제는 점이 연속적인 움직임과 삽입 및 삭제를 모두 겪기 때문에 최소 신장 트리를 유지할 수 있는 운동 데이터 구조를 요구합니다.여러 논문에서 이러한 구조를 연구했으며,^{[41][42][43][44][45]} 교환 횟수의 경계와 거의 일치하는 입방체에 가까운 총 시간을 가진 대수적으로 움직이는 점에 대한 운동 구조가 알려져 있습니다.^[44]

하한값

유클리드 최소 신장 트리 $문제$의 ω (n ${\displaystyle \log }$⁡ ${\displaystyle n}$) ${\displaystyle \Omega (n\log$ n$)}$의 점근적 하한을 제한된 계산 모델에서 설정할 수 있습니다.여기에는 알고리즘이 좌표에 간단한 대수 계산을 수행하는 특정 제한된 프리미티브를 통해서만 입력 지점에 액세스할 수 있는 대수적 결정 트리 및 대수 계산 트리 모델이 포함됩니다.이러한 모델에서 가장 가까운 점 쌍 문제는 ω${\displaystyle (n}$ ${\displaystyle \log }$ ⁡ n${\displaystyle }$) ${\displaystyle \Omega(n\log$ n$)}$ 시간이 필요하지만 가장 가까운 쌍은 반드시 최소 신장 트리의 가장자리이므로 최소 신장 트리도 이 정도의 시간이 필요합니다.따라서 예를 들어 들라우네 삼각 분할법을 사용하여 이 모델 내에서 O $시간{\displaystyle (n}$ ${\displaystyle \log }$ ⁡ ${\displaystyle n}$ )${\displaystyle O(n\log$ n$)}$에 평면 최소 신장 트리를 구성하는 알고리듬이 최적입니다.그러나 이러한 하한은 해당 좌표에 대한 비트 와이즈 연산 및 테이블 인덱싱 연산이 허용되는 정수 점 좌표를 사용하는 계산 모델에는 적용되지 않습니다.이러한 모델에서는 위에서 설명한 것처럼 더 빠른 알고리즘이 가능합니다.^[26]

적용들

유클리드 최소 신장 트리의 명백한 적용은 링크가 단위 길이당 고정된 양이라고 가정할 때, 한 세트의 장소를 연결하기 위해 가장 저렴한 와이어 또는 파이프 네트워크를 찾는 것입니다.최소 신장 트리에 대한 최초의 출판물은 모라비아 남부를 위한 전기 그리드의 설계를 포함하는 문제의 지리적 버전에 더 일반적으로 관한 것이었고,^[47] 회로에서 전선 길이를 최소화하기 위한 적용은 1957년 Loberman과 Weinberger에 의해 기술되었습니다.^[48]

최소 신장 트리는 계층적 클러스터링을 위한 여러 방법 중 하나인 단일 링크 클러스터링과 밀접한 관련이 있습니다.최소 신장 트리의 가장자리는 길이에 따라 정렬되며 이 클러스터링 방식으로 클러스터를 더 큰 클러스터로 병합하는 순서를 제공합니다.이러한 에지가 발견되면, 알고리즘에 따라 O $시간{\displaystyle (n}$ ${\displaystyle \log }$ ⁡ ${\displaystyle n)}$ ${\displaystyle O(n\log$ n$)}$에 단일 링크 클러스터링을 구성하는 데 사용될 수 있습니다$.$ 단일 링크 클러스터링으로 생성된 길고 얇은 클러스터 모양은 가우스 분포의 혼합과 같은 특정 유형의 데이터에 적합하지 않을 수 있지만, 이는 좋은 ch일 수 있습니다.은하계의 암흑 물질 후광을 모델링할 때와 같이 성단 자체가 길고 얇은 모양을 가질 것으로 예상되는 응용 분야의 얼음.^[5]지리 정보 과학에서 몇몇 연구자 그룹은 건물의 중심부의 최소 신장 트리를 사용하여 건물의 의미 있는 클러스터를 식별했습니다. 예를 들어 다른 방법으로 일관성이 없는 것으로 식별된 가장자리를 제거하는 것입니다.^[49]

최소 신장 트리는 또한 곡선을 따라 샘플링된 점이 주어진 평면에서 곡선 모양을 추론하는 데 사용되었습니다.로컬 피쳐 크기보다 미세하게 샘플링된 부드러운 곡선의 경우 최소 신장 트리는 곡선을 따라 연속된 점을 연결하는 경로를 형성합니다.일반적으로 비슷한 방법으로 연결된 단일 집합이 아닌 점선 또는 점선 스타일로 그려진 곡선을 인식할 수 있습니다.이 곡선 찾기 기술의 응용에는 입자가 거품 챔버에 남긴 흔적을 자동으로 식별하는 입자 물리학이 포함됩니다.^[50]이 아이디어의 더 정교한 버전은 스패닝 트리의 토폴로지를 사용하여 최소 제곱 이동 방법을 안내함으로써 곡선 윤곽을 대략적으로 따르는 잡음이 많은 샘플 포인트 구름에서 곡선을 찾을 수 있습니다.^[51]

최소 신장 트리의 또 다른 적용은 유클리드 여행 세일즈맨 문제, 점 집합의 최단 다각화를 찾는 문제에 대한 상수 인자 근사 알고리듬입니다.최소 신장 트리의 경계를 걸어 다니면 최적의 길이의 2배 이내로 최적의 여행 세일즈맨 투어를 근사화할 수 있습니다.^[2]그러나 이 문제에 대해 더 정확한 다항식 시간 근사 체계가 알려져 있습니다.^[52]무선 애드 혹 네트워크에서, 최소 신장 트리의 경로를 따라 메시지를 브로드캐스트하는 것은 최소 에너지 브로드캐스트 라우팅에 대한 정확한 근사치가 될 수 있으며, 이는 다시 정확히 계산하기 어렵습니다.^{[53][54][55][56]}

깨달음

유클리드 최소 신장 트리에 대한 실현 문제는 추상 트리를 입력으로 하고 주어진 트리가 해당 점의 최소 신장 트리와 동일하도록 트리의 각 정점(일부 고정된 차원의 공간)에 대한 기하학적 위치를 찾습니다.모든 추상적인 트리가 그러한 깨달음을 가지고 있는 것은 아닙니다. 예를 들어, 트리는 각 정점의 정도에 구속된 키싱 수에 따라야 합니다.예를 들어 평면 최소 신장 트리가 5도 또는 6도의 정점에 인접한 6도의 정점을 갖는 것은 불가능합니다.^[7]2차원 구현이 존재하는지 여부를 결정하는 것은 NP-hard입니다.그러나 경도의 증명은 트리의 6도 정점이 매우 제한된 실현 집합을 가지고 있다는 사실에 달려 있습니다. 이러한 정점의 이웃은 해당 정점에 중심을 둔 정육각형의 정점에 배치되어야 합니다.^[57]실제로 최대 5도의 나무의 경우 항상 평면적인 실현이 존재합니다.^[7]마찬가지로 최대 10도의 나무에 대해서도 항상 3차원의 실현이 존재합니다.^[10]이러한 실현을 위해 일부 트리는 가장 짧은 에지의 길이에 대해 지수 길이의 에지와 지수 영역의 경계 상자가 필요할 수 있습니다.^[58]최대 차수 4의 트리는 다항식 경계 에지 길이와 경계 상자가 있는 더 작은 평면 현실화를 가집니다.^[9]

참고 항목

• 직선형 최소 신장 트리, 택시 지오메트리를 이용하여 거리를 측정한 최소 신장 트리

참고문헌

외부 링크

• EMST 자습서, mlpack 설명서