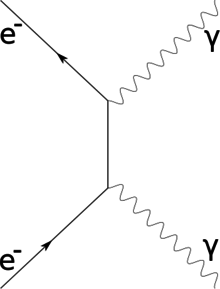
전자 산란

산란 유형
전자빔이 핵 N, 전자 껍질 K,L,M과 샘플과 어떻게 상호작용하는지를 그림으로 기술한다. 전송된 전자와 탄성/불탄성 산란 전자를 보여준다. SE는 빔 전자에 의해 방출되는 2차 전자로서, 특징적인 광자(X-Ray) γ을 방출한다. BSE는 백-스캐터 전자, 즉 표본을 통해 전달되는 대신 뒤쪽으로 흩어지는 전자다.
전자( e− , β− )
입자	전자
미사	9.16838291(40)×10kg−31[1] 5.4857990946(22)×10−4 u[1] [1822.8884845(14)]−1 u[note 1] 0.510998928(11) MeV/c2[1]
전하	−1 e[주2] -1.6021765(35)×10−19 C[1] −4.80320451(10)×10−10 esu
마그네틱 모멘트	−1.00115965218076(27) μB[1]
스핀	1⁄2
산란
힘/효과	로렌츠 힘, 정전력, 중력, 약한 상호작용
방안	충전, 전류
분류	탄성 충돌, 비탄성 충돌, 고에너지, 저에너지
상호작용	e-e-− − e e-− γ e-e-− + e e-p− e-n− e− — 핵
종류들	콤프턴 산란 뫼르 산란 모트 산란 하바 산란 브렘스스트라흘룽 깊은 비탄성 산란 싱크로트론 방출 톰슨 산란

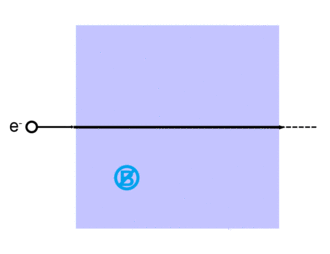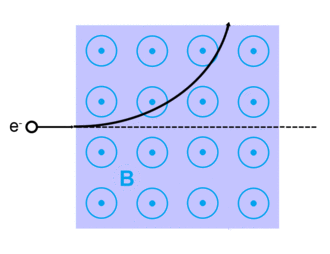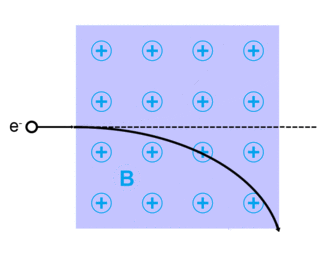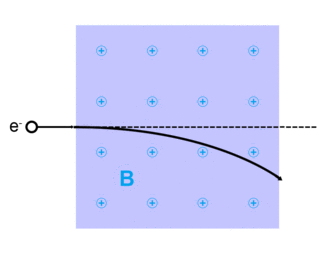
전자 산란은 전자가 원래 궤적에서 이탈할 때 발생한다. 이는 물질 상호작용 내의 정전력이나 외부 자기장이 존재하는 경우 전자가 로렌츠 힘에 의해 비껴갈 수 있기 때문이다.^{[2][3][citation needed][4][5]} 이러한 산란은 일반적으로 금속, 반도체 및 절연체와 같은 고형물에서 발생하며,^[6] 집적회로 및 트랜지스터의 제한 요인이다.^[2]

전자 산란 적용은 핵 및 핵구조물의 전하 분포를 측정할 수 있는 해드론 시스템용 고해상도 현미경으로 활용할 수 있는 것이다.^[7][8] 전자의 산란으로 양자와 중성자가 쿼크라고 불리는 작은 초등 아원자 입자로 이루어져 있다는 것을 이해할 수 있게 되었다.^[2]

전자는 다음과 같은 여러 가지 방법으로 고체를 통해 산란될 수 있다.

• 전혀 그렇지 않다: 전자 산란 현상이 전혀 일어나지 않고 빔이 직선으로 통과한다.
• 단일 산란: 전자가 단 한 번만 산란할 때.
• 복수 산란: 전자가 여러 번 산란할 때
• 다중 산란: 전자가 여러 번 산란할 때.

전자 산란 확률과 산란 정도는 평균 자유 경로에 대한 표본 두께의 확률 함수다.^[6]

역사

전자의 원리는 1838년에서 1851년 사이에 자연 철학자 리처드 라밍이 처음으로 이론화했는데, 그는 원자핵이 물질핵을 둘러싸고 있는 전기 입자의 동심원 껍질의 '전기적 조개'라고 생각했다.^{[9][note 3]}

비록 전하 입자 이론의 발달에 있어서 다른 주목할 만한 멤버는 조지 존스톤 스토니(전자기라는 용어를 창안한 사람), 에밀 위처트(전자의 독립적 발견을 최초로 출판한 사람), 월터 카우프만(Walter Kaufmann), 피터 지만(Pieter Zeeman), 헨드리크 L(Hendrik L)이지만, J. 톰슨이 1897년에 처음으로 전자를 발견했다는 것이 일반적으로 받아들여진다.오렌츠^[10]

콤프턴 산란은 1923년 워싱턴대에서 1927년 노벨물리학상을 받은 아서 콤프턴에 의해 처음 관찰됐다. 그의 대학원생 Y. H. Woo도 그 결과를 추가로 검증했다. 콤프턴 산란은 보통 원자의 전자와 관련된 상호작용에 관하여 인용되지만 핵 콤프턴 산란이 존재한다.^{[citation needed]}

최초의 전자 회절 실험은 1927년 클린턴 데이비슨과 레스터 게머에 의해 현대 LEED 시스템의 프로토타입이 될 것을 이용하여 수행되었다.^[11] 이 실험은 전자의 파동 같은 특성을 증명할 수 있었고,^{[note 4]} 따라서 물질 입자는 파동 같은 성질을 가지고 있다는 드 브로글리 가설을 확인할 수 있었다.^{[citation needed]} 그러나, 이 후 LEED에 대한 관심이 되살아난 1960년대 초까지 고에너지 전자 회절(High-energy electron diffraction)을 선호하여 LEED에 대한 관심이 줄어들었다. 이 기간 동안 주목할 만한 언급은 LEED 기술을 계속 발전시킨 H. E. Farnsworth가 있다.^[11]

고에너지 전자전자 충돌빔 역사는 1956년 K에서 시작된다. 프린스턴 대학의 O'Neill은 높은 에너지 충돌에 관심을 갖게 되었고, 스토리지 링에 가속기를 주입하는 아이디어를 소개했다. 빔과 빔의 충돌에 대한 생각은 대략 1920년대부터 존재해 왔지만, 1953년에 이르러서야 충돌 빔 장치에 대한 독일의 특허가 롤프 위더뢰에에 의해 획득되었다.^[12]

현상

전자는 정전기 쿨롱의 힘을 통해 다른 충전된 입자에 의해 산란될 수 있다. 더욱이 자기장이 존재한다면, 움직이는 전자는 로렌츠 힘에 의해 굴절될 것이다. 양자 및 상대론적 측면을 포함한 모든 전자 산란에 대한 극히 정확한 설명은 양자 전자역학 이론에 의해 제시된다.

로렌츠 힘

네덜란드 물리학자 헨드릭 로렌츠의 이름을 딴 로렌츠 힘은 충전된 입자 q에 대해 다음과 같은 방정식으로 주어진다.^[13]

${\displaystyle \mathbf {F} =q\mathbf {E} +q\mathbf {v} \times \mathbf {B}}}$

여기서 qE는 q에 작용하는 현재의 전기장 E로 인한 전기력을 설명한다.
그리고 qv x B는 q가 속도 v로 움직일 때 q에 작용하는 현재의 자기장 B로 인한 자력을 설명한다.^[13][14]
또한 다음과 같이 기록될 수 있다.

${\displaystyle \mathbf {F} =q[-\nabla \phi -{\frac {d\mathbf {A}}}{dt}+\nabla(\mathbf {A}\cdot \mathbf {v} )]}}$

여기서 $\varphi {\displaystyle }$ ${\displaystyle \phi }$은(는) 전위이고, A는 자기 벡터 전위임.^[15]

1885년과 1889년에 qv x B의 로렌츠 힘에 대한 정확한 표현을 처음으로 도출한 것으로 추정되는 사람은 올리버 헤비사이드였다.^[16]헨드릭 로렌츠는 1892년에 그 개념을 도출하고 정제하여 전기장으로 인한 힘을 통합하여 ^[17]그의 이름을 붙였다.
이것을 전하 q 질량 m의 자유 입자에 대한 운동 방정식으로 다시 쓰면 다음과 같이 된다.^[13]

${\displaystyle m{\frac {d\mathbf {v}}{dt}=q\mathbf {E} +q\mathbf {v} \times \mathbf {B}}}}$

또는

${\displaystyle m{\frac {d\gamma \mathbf {v}}{dt}=q\mathbf {E} +q\mathbf {v} \times \mathbf {B}}}}$

로렌츠 수축을 사용한 상대론적 사례에서 γ은 다음과 같다.^[18]

${\displaystyle \cHB(v)\equiv {1}{\frac {1}{1-v^{2}/c^{2}}}}$

이 운동 방정식은 1897년 J. J. 톰슨의 자기장 내 광선의 굴절을 통해 이 광선이 현재 전자라고 알려진 전하 입자의 흐름임을 확인한 음극선을 조사하는 실험에서 처음 검증되었다.^[10][13]

이 기본 공식에 대한 변화들은 전류를 운반하는 와이어(라플라스 힘이라고도 함), 자기장을 통해 이동하는 와이어 루프에 있는 기전력(파라데이의 유도 법칙의 한 측면) 및 빛의 속도 근처로 이동할 수 있는 입자에 대한 힘(로렌츠 의 상대적 형태)을 설명한다.ce.

정전기 쿨롱 힘

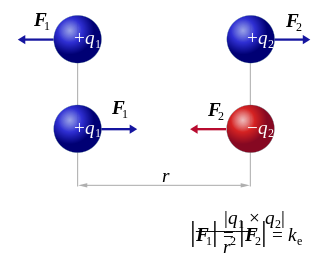
1785년에 결과를 발표한 Charles-Augustin de Coulomb의 이름을 딴 Coulomb 상호작용과 정전기력이라고도 알려진 정전기는 전하에 의한 입자의 끌어당김이나 반발에 대해 설명한다.^[19]

쿨롱의 법칙은 다음과 같이 명시하고 있다.

두 점 전하 사이의 전기력의 크기는 전하 산출물에 정비례하며, 두 점 전하 사이의 거리의 제곱에 반비례한다.^[20][주5]

정전력의 크기는 전하 크기의 스칼라 배수에 비례하고 거리의 제곱(즉 역제곱법)에 반비례하며, 다음과 같이 주어진다.

${\displaystyle F=k{\frac {q_{1}q_{2}}{{r^{2}}={\frac {q_{1}q_{2}{4\pi \epsilon _{0}r^{2}}:}$

또는 벡터 표기법:

${\displaystyle \mathbf {F} =k{\frac {q_{1}q_{2}}{ \mathbf {r} ^{2}}}\mathbf {\hat {r}} ={\frac {q_{1}q_{2}}{4\pi \epsilon _{0} \mathbf {r} ^{2}}}\mathbf {\hat {r}} }$

여기서, q₁₂,q는 두 개의 서명된 점 전하이다; r-hat는 전하 사이의 거리 r의 단위 벡터 방향이다; k는 쿨롬브 상수이고 ε은₀ SI 단위로 주어지는 자유 공간의 허용률이다.^[20]

${\displaystyle k={\frac {1}{4\pi \epsilon _{0}\\약 8.988\limit 10^{9}}Nm^{2}{C^{-}^{2}}:$

${\displaystyle \epsilon _{0}\times 약 8.854\{-12}C^{2}N^{-1}m^{-2}}회$

두 전하가 서로 작용하는 힘의 방향은 항상 서로 연결되는 직선을 따라 움직이며(최단 거리), 무한대의 벡터 힘이며, 뉴턴 제3법칙은 크기가 같고 방향이 반대다. 또한, 전하 q와₁ q의₂ 부호가 같을 때(양 또는 모두 음) 그들 사이의 힘이 역겨워지며, 반대 기호가 있으면 그 힘이 매력적이다.^[20][21] 이러한 힘은 세 번째 전하가 도입되면 그 전하에 작용하는 총력이 다른 전하가 개별적으로 발휘하는 힘의 벡터 합이라는 힘의 중첩 원칙이라는 중요한 속성을 준수하며, 이것은 어떤 수의 전하를 보유한다.^[20] 그러나, Coulomb's Law는 진공 상태에서 요금에 대해 명시되었다. 포인트 요금 사이의 공간에 물질이 포함되어 있다면, 요금 간의 허용성은 다음과 같이 설명되어야 한다.

${\displaystyle F=k{\frac {q_{1}q_{2}{{}{{\엡실론 _{r}r^{2}}:}$

여기서 ε은_r 힘이 작용하고 치수가 없는 공간의 상대적 자유도 또는 유전 상수다.^[20]

충돌

산란 과정에서 두 입자가 서로 상호작용하는 경우, 상호작용 후 두 가지 결과가 가능하다.^[22]

탄성

탄성 산란이란 대상 입자와 입사 입자 간의 충돌이 운동에너지를 완전히 보존하는 것을 말한다.^[23] 이는 입자의 분해나 진동을 통한 에너지 손실이 없다는 뜻으로,^[23][24] 즉 각 입자의 내부 상태는 변하지 않고 있다는 것을 의미한다.^[22] 끊어지는 존재가 없기 때문에 탄성 충돌은 전자와 같은 기초 입자에 매우 유용한 원리인 ^[24]점성 입자 사이에서 일어나는 것으로 모델링할 수 있다.^[22]

비탄성적

비탄성 산란이란 충돌로 운동에너지가 보존되지 않아 ^[23][24]한 입자 또는 두 입자의 내부 상태가 모두 변했을 때를 말한다.^[22] 이는 에너지가 진동으로 변환되기 때문이며, 이는 열, 파동(소리), 또는 충돌 당사자의 구성 입자 사이의 진동으로 해석될 수 있다.^[23] 입자들은 또한 분열될 수 있고, 추가 에너지는 성분들 사이의 화학적 결합을 깨뜨리는 것으로 변환될 수 있다.^[23]

또한 탄성 및 비탄성 산란에서 탄력이 유지된다.^[23] 산란 이외의 다른 결과는 상호작용하는 입자의 구조가 변화하여 일반적으로 둘 이상의 복잡한 입자가 생성되는 반응과 상호작용하는 입자의 구성 요소인 기본 입자가 아닌 새로운 입자가 생성되는 반응이다.^[22][23]

기타 산란 유형

전자 분자 산란

고립된 원자와 분자에 의한 전자 산란은 가스 단계에서 발생한다. 이것은 플라즈마 물리학과 화학에서 중요한 역할을 하며 반도체 물리학과 같은 응용 분야에 중요하다. 전자 분자/원자 산란은 일반적으로 양자역학을 통해 처리된다. 단면을 계산하기 위한 선도적인 접근방식은 R-매트릭스 방법을 사용하는 것이다.

콤프턴 산란

콤프턴 산란은 1922년에 처음 효과를 관측하여 1927년 노벨 물리학상을 받은 아서 콤프턴의 이름을 딴 것으로, 자유 전하 입자에 의한 고에너지 광자의 비탄성 산란이다.^{[25][26][note 6]}

이는 1923년 기존의 방사선 이론과 일치하지 않는 방식으로 산란된 포일(탄소 표적)을 통해 주어진 파장(특정 사례의 X선)의 방사선을 발사함으로써 입증되었다.^{[26][note 7]} 콤프턴은 '물리 리뷰'에 그 현상을 설명하는 논문을 발표했다: 빛 원소에 의한 X선 산란 양자 이론이다.^[27] 콤프턴 효과는 들어오는 광자가 에너지의 일부를 전자에 주면 산란된 광자는 플랑크 관계에 따라 에너지와 주파수가 낮고 파장이 길어지는 개별 전자에서 탄성적으로 산란하는 고에너지 광자로 이해할 수 있다.^[26][28]

$[\displaystyle E=h=h\nu =hf}$

주파수 f 또는 ν 단위로 광자의 에너지 E와 Planck의 상수 h(6.626×10⁻³⁴ J⋅s = 4.136×10⁻¹⁵ eV.s)^[29]를 제공한다. 그러한 산란에서 파장의 변화는 주어진 표적 입자에 대한 산란 각도에 의해서만 결정된다.^[28][30]

이것은 광전 효과에 의해 제안된 빛의 입자(사진) 성질이 여전히 논의되고 있던 1920년대에 중요한 발견이었는데, 콤프턴 실험은 입자 유사 행동의 명확하고 독립적인 증거를 제공했다.^[25][30]

산란으로 인한 파장의 콤프턴 이동을 설명하는 공식은 다음과 같다.

${\displaystyle \f}-\ftda _{i}={\frac {h}{m_{e}c}}(1-\cos \theta )}$

여기서 λ은_f 산란 후 광자의 최종 파장, λ은_i 산란 전 광자의 초기 파장, h는 플랑크의 상수, m은_e 전자의 나머지 질량, c는 빛의 속도, θ은 광자의 산란각이다.^[25][30]

(1 - cos θ)의 계수는 콤프턴 파장이라고 알려져 있지만, 사실 파장 이동에 대한 비례 상수다.^[31] 충돌은 광자 파장을 0도(0° 산란 각도)에서 콤프턴 파장(180°^[32] 산란 각도)의 2배까지 증가시킨다.

톰슨 산란은 산란 과정의 고전적인 탄력적 양적 해석이며,^[26] 이것은 낮은 에너지의 광자와 중간 에너지의 양적 해석으로 볼 수 있다. 전하 입자에 의해 산란된 전자파의 고전적 이론은 파장의 저강도 변화를 설명할 수 없다.

역 콤프턴 산란은 전자가 움직일 때 발생하며 광자에 비해 운동 에너지가 충분하다. 이 경우 순 에너지가 전자에서 광자로 전달될 수 있다. 역 콤프턴 효과는 낮은 에너지 광자(예: 우주 마이크로파 배경)가 높은 에너지(상대성) 전자를 튕겨낼 때 천체물리학에서 나타난다. 그러한 전자는 초신성과 활성 은하핵에서 생성된다.^[26]

뫼르 산란

모트 산란

하바 산란

브렘스스트라흘룽 산란

깊은 비탄성 산란

싱크로트론 방출

전자와 같은 충전된 입자가 가속되는 경우(직선에서의 가속이나 곡선 경로에서의 동작일 수 있음) 전자기 방사선이 입자에 의해 방출된다. 전자 저장 링과 싱크로트론(synchrotron)으로 알려진 원형 입자 가속기 안에서 전자는 원형 경로로 구부러지고 전형적으로 X선을 방출한다. 이 방사상 방출(${\displaystyle \mathbf{}}$ 입자가 가속될 때${\displaystyle v\mathbf{}}$ v ${\$) 전자기 방사선을 싱크로트론 방사선이라고 한다.^[33] 그것은 구부러진 자석, 불연속기 및/또는 위글러를 사용하여 싱크로트론에서 생산된다.^{[citation needed]}

첫 번째 관측은 1947년 4월 24일 허브 폴락 팀이 RF 가속기의 위상안정성 원리를 시험하기 위해 구축한 싱크로트론에 있는 뉴욕주 쉐넥타디의 일반전기연구소에서 나왔다.^{[note 8]} 정비사에게 튜브의 불꽃을 확인하기 위해 커다란 거울로 차폐물을 둘러보라는 요청을 받았을 때, 그는 전자빔에서 밝은 아크가 나오는 것을 보았다. 로버트 랭무어는 이것을 싱크로트론 방사선이나 줄리안 슈윙거의 이름을 따서 "슈윙거 방사선"으로 인식한 공로를 인정받고 있다.^[34]

고전적으로 가속 전자에서 복사 전력 P는 다음과 같다.

${\displaystyle P={\frac {2Ke^{2}}:{3c^{2}}:a^{2}}:2}}:$

이것은 Larmor 공식에서 온다. 여기서 K는 전기적 순열도 상수,^{[note 9]} e는 전자 전하, c는 빛의 속도, a는 가속도다. 저장고리와 같은 원형 궤도 안에서 비상대적 경우는 단순히 구심 가속이다. 그러나 스토리지 링 내에서 가속은 매우 재실현적이며 다음과 같이 얻을 수 있다.

${\displaystyle a_{non-relativistic}={\frac {v^{2}}{r}}\rightarrow a_{relativistic}={\frac {1}{m}}{\frac {dp}{d\tau }}={\frac {1}{m}}\gamma {\frac$${d(\vmv)}{dt}=\frac ^{2}{{dt}=\$frac }{dt$}=\frac ^{v^{2$}}{$r$

여기서 v는 원형 속도, r은 원형 가속기의 반지름, m은 충전된 입자의 나머지 질량, p는 운동량, τ은 적정 시간(t/γ), γ은 로렌츠 계수다. 그러면 복사 전력이 다음과 같이 된다.

${\displaystyle P={\frac{2Ke^{2}}:{3c^{2}}:{3c^{2}}:2}}:{\frac {2Ke^{2}}:{3c^{2}}:}{\frac {\frac}{4}v^{4}{r^{2}}:2}}:}$

매우 상대론적 입자들의 경우 그러한 그 속도 거의, 그 입자 에너지 γmc2의 4이 손실 규모 손실률 결정의γ4 용어가 지배적인 변수, 싱크로트론 복사 손실의 반경 argues에 가속기도 possib로 큰 설립을 역 의존도 일정하게 된다.르.^[33]

시설.

슬락

스탠포드 선형가속기 센터는 캘리포니아 주 스탠퍼드 대학교 근처에 위치해 있다.^[35] 1962년 2마일 길이의 선형가속기에서 공사가 시작되어 1967년에 완공되었으며, 1968년 SLAC의 리처드 테일러와 제롬 1세가 공유한 1990년 노벨 물리학상을 계기로 쿼크의 첫 실험 증거가 발견되었다. MIT의 프리드먼과 헨리 켄달.^[36] 가속기는 전자 가속을 위한 20GeV 용량을 가지고 나왔고, 러더포드의 산란 실험과 유사하지만, 그 실험은 겨우 7MeV의 알파 입자로 작동했다. SLAC 사례에서 입사 입자는 전자였고 대상자는 양성자였으며, 전자 파장은 짧기 때문에(높은 에너지와 운동량 때문에) 양성자를 탐사할 수 있었다.^[35] SLAC에 추가된 스탠포드 포시트론 전자 비대칭 링(SPEAR)은 그러한 발견을 더욱 가능하게 하여 1974년에 J/psi 입자가 발견되었는데, 이 입자는 짝을 이룬 매력 쿼크와 반-차르 쿼크로 구성되어 있으며, 1976년에는 또 다른 노벨 물리학상을 수상하였다. 이는 마틴 펄이 1995년 노벨 물리학상을 공동 수상했던 타우 렙톤을 발견했다고 발표한 데 따른 것이다.^[36]

SLAC는 최고의 가속기 실험실이 되고,^[37] 입자 물리학, 입자 천체 물리학, 우주론에서의 전략적인 프로그램뿐만 아니라 치유를 위한 신약, 전자 장치를 위한 신소재 그리고 깨끗한 에너지를 생산하고 환경을 정화하기 위한 새로운 방법들을 발견하는 응용 프로그램들을 추구하는 것을 목표로 한다.^[38] SLAC의 다섯 번째 이사인 치창 카오의 감독(2012년 11월 기준)에 따라 2010년 SLAC에 와서 스탠포드 싱크로트론 방사선 광원 부연구실장을 역임한 저명한 X선 과학자가 있다.^[39]

바바

SSRL - 스탠포드 싱크로트론 방사선 광원

SLAC에서 실행되는 기타 과학 프로그램에는 다음이 포함된다.^[40]

• 어드밴스트 액셀러레이터 리서치
• ATLAS/대형 하드론 충돌기
• 기초 입자 이론
• EXO - 농축 제논 관측소
• FACET - 첨단가속기 실험용 설비
• 페르미 감마선 우주 망원경
• 갠트4
• KIPAC - 입자 천체물리학 및 우주론 연구소
• LCLS - Linac 일관성 있는 광원
• LSST - 대형 시냅스 측량 망원경
• NLCTA - 다음 선형 충돌기 테스트 가속기
• 스탠퍼드 펄스 연구소
• SIMES - Stanford 재료 및 에너지 과학 연구소
• SUNCAT 인터페이스 과학 및 카탈루션 센터
• 슈퍼 CDMS - 슈퍼 극저온 암흑 물질 검색

RIKEN RI 빔 공장

RIKEN은 1917년 도쿄의 민간연구재단으로 설립되었으며, 일본 최대의 종합연구기관이다. 규모와 범위가 급성장한 이곳은 오늘날 다양한 과학분야의 수준 높은 연구로 유명하며, 일본 전역의 세계적인 연구센터와 연구소의 네트워크를 망라하고 있다.^[41]

RIKEN RI Beam Factory는 RIKEN Nishina Centre (가속기 기반 과학을 위한)라고도 알려져 있으며, 2007년에 운영을 시작한 사이클로트론 기반 연구 시설로, 일본 사이클로트론에서 최초로 개발된 지 70년 후, 닥터 로부터의 것이다. 시설에 이름이 붙여진 니시나 요시오.^[42]

2006년 현재 이 시설에는 세계적인 중이온가속기 단지가 있다. 이것은 K540-MeV 링 사이클로트론(RRC)과 두 개의 다른 인젝터, 즉 가변 주파수 헤비이온 라이낙(RILAC)과 K70-MeV AVF 사이클로트론(AVF)으로 구성된다. 세계에서 가장 강도가 높은 광원자질량 RI 빔인 60au 미만의 RI(방사능 동위원소) 빔을 제공하는 발사체-파쇄 분리막(RIPS)을 탑재했다.^[43]

니시나 센터가 감독하는 RI 빔 팩토리는 핵, 입자, 하드론 물리학 분야의 연구를 촉진하는 전 세계 사용자들에 의해 이용되고 있다. 이러한 가속기 응용연구의 촉진은 니시나 센터의 중요한 임무로서, 국내 및 해외 가속기 설비의 이용을 실시한다.^[44]

스크리트

SCRIT(자체정립방사성동위원소 이온대상) 설비는 현재 일본 RIKEN RI 빔 공장(RIBF)에서 건설 중이다. 이 프로젝트는 전하 밀도 분포의 탄성 전자 산란 시험을 통해 단수 핵에 대한 조사를 목표로 하며, 초기 시험은 안정 핵으로 한다. 불안정한 Sn 동위원소에서 전자가 처음으로 산란되면서 2014년에 발생하게 된다.^[45]

단수명 방사능 핵 전자 산란의 방법으로(R1)의 조사는 무능 이 핵은 target,[46]현재 세계 최초의 시설의 소설self-confining R1기술은 핵의 구조체의 전자 산란 번째에 의해 연구에 전용의 도래로 인해 점검 내용을 수행한 적이 없었다.r은에스테크는 가능해진다. 이 기법의 원리는 전자 저장 링 시설에서 관측되는 이온 트래핑 현상을 중심으로 하여 전자 저장 링의 성능에 악영향을 미친다.^{[note 10][45]}

SCRIT에 채택될 새로운 아이디어는 산란 실험에 전자빔에 갇힌 이온으로 단명된 RI를 표적으로 만들기 위해 이온 트래핑을 사용하는 것이다. 이 아이디어는 교토대학의 전자 저장 링인 KSR을 이용한 원리 증명 연구가 먼저 이루어졌는데, 이는 120MeV 전자 빔 에너지, 75mA의 대표적인 저장 빔 전류 및 100초 빔 수명을 실험한 결과 Cs의 안정된 핵을 표적으로 삼았다. 이 연구의 결과는 갇힌 C에서 나오는 탄성적으로 산란된 전자가 선명하게 보이는 것에 유리했다.^[45]

참고 항목

• 지만 효과
• 입자물리학
• 저에너지 전자회절
• 양자전기역학
• R 매트릭스

메모들

참조

외부 링크

• 물리학 소리: 전자 산란(비디오)
• 브라이트스톰: 콤프턴 산란(비디오)