고전 XY 모형
Classical XY model고전 XY 모형(고전 회전자(회전자) 모형 또는 O(2) 모형이라고도 함)은 통계 역학의 격자 모형입니다.일반적으로 XY 모형은 n = 2에 대한 Stanley의 n-입자[1] 모형 전문화로 볼 수 있습니다.
정의.
D차원 격자 δ가 주어졌을 때, 각 격자 부위 j δ δ마다 2차원 단위 길이 벡터j s =(cos δj, sin δj)가 있다.
스핀 구성 s = (sj)j ∈ Λ는 각 j δ에 대한 각도 -θ < θj θ θ의 할당이다.
변환-등가 상호작용ij J = J(i - j) 및 점 의존 외부 j ( j ,) { _}=(가 주어지면 구성 에너지는 다음과 같습니다.
ij 가장 가까운 이웃을 제외하고 J = 0인 경우를ij 가장 가까운 이웃 대소문자라고 합니다.
구성 확률은 역온도β 0 0의 볼츠만 분포로 구할 수 있다.
여기서 Z는 정규화 또는 파티션 [2]함수입니다.표기법 A(s ) { A ( \ )\는 주기적인 경계 조건이 적용된 후 무한 볼륨 제한에서 랜덤 변수 A의 기대를 나타냅니다.
엄격한 결과
- 자유 에너지와 스핀 상관관계에 대한 열역학 한계의 존재는 지니브에 의해 증명되었고, 이 경우 그리피스 [3]부등식으로 확장되었다.
- Ginibre, Aizenman과 Simon[4]의 입 안이 그리피스 불평등 사용하면 치수 D의 ferromagnetics XY모델, J를 결합, 0과 역 temperatureβ의 2점 스핀 상관 관계(즉 상한에 의해 제공했다)에 의해 치수 D의ferromagneticIsing 모델, 연결 장치의 2점 상관 관계를 지배하고 있는 것을 증명했다.J>0그리고 역 온도.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.border-top:1px}고체.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}β/2 따라서 XY 모델의 임계 β는 Ising 모델의 임계 온도의 두 배보다 작을 수 없습니다.
일차원
자유(비주기적) 경계 조건을 가진 모든 '가장 가까운' n-벡터 모델에서와 마찬가지로 외부 필드가 0이면 단순하고 정확한 솔루션이 존재합니다.자유 경계 조건의 경우, 해밀토니안은
열역학적 한계에서도 비열은 발산되지 않습니다.실제로 1차원 이싱 모델과 마찬가지로 1차원 XY 모델도 유한 온도에서 위상 전이가 없습니다.
주기적 경계 조건(그리고 여전히 h = 0)에 대한 동일한 계산은 결과는 [6]동일하지만 전달 행렬 형식을 필요로 한다.
파티션 함수는 다음과 같이 평가할 수 있습니다.
이 전송 매트릭스 어프로치는 자유 경계 조건을 사용하는 경우에도 필요합니다만, 적용 가 0h\ 0 필드 h h가 제로 필드의 시스템에 대한 섭동으로 취급할 수 있을 정도로 작을 경우 자기 민감도 )가 됩니다. M h를 추정할 수 있습니다.이는 전달 행렬 접근법에 의해 계산된 고유 상태를 사용하고 2차 섭동 이론으로 에너지 이동을 계산한 다음 자유 에너지 F 0- 1 2{\ F h과와)를 비교함으로써 이루어진다.
2차원
가장 가까운 이웃 상호작용을 가진 2차원 XY 모델은 메르민-워그너 정리에 의해 요구되는 장거리 순서를 가지지 않는 연속 대칭을 가진 2차원 시스템의 한 예이다.마찬가지로 대칭 파괴와 관련된 일반적인 위상 전이는 존재하지 않습니다.그러나 나중에 논의될 것처럼, 시스템은 무질서한 고온 상태에서 임계 온도 이하인 준질서 상태로 전환되는 징후를 보입니다. 이를 Kostlerlitz-Thouless 전이라고 합니다.스핀의 이산 격자의 경우, 2차원 XY 모델을 전송 매트릭스 어프로치를 사용해 평가할 수 있어 모델을 고유치 문제로 환원하고 전송 매트릭스로부터의 최대 고유치를 이용한다.정확한 용액은 다루기 어렵지만, 저온에서 발생하는 T cc {\c}}에 대한 추정치를 얻기 위해 특정 근사치를 사용할 수 있다.예를 들어, Mattis(1984)는 시스템의 임계 온도를 추정하기 위해 이 모델에 대한 근사치를 사용했다.
더욱이, 통계역학을 사용하여 열역학적 평균을 계산함으로써 특정 열과 같은 양에 연관시킬 수 있다.
임계 전이 및 소용돌이 형성의 특성은 XY 모델의 연속 버전을 고려함으로써 설명할 수 있습니다.여기서 이산 스핀 n})은 공간 내 임의의 점에서의 스핀 각도를 나타내는 필드( {로 대체됩니다.이 경우 회전각도 () \ ( \ { x )는 위치 변경에 따라 부드럽게 변화해야 합니다.테일러 급수로서 원래의 코사인(cosine)을 확장하면, 해밀토니안은 연속체 근사에서 다음과 같이 표현될 수 있다.
XY 모델의 연속 버전은 종종 초유체 헬륨, 육각 액정 등 동일한 종류의 대칭을 갖는 순서 매개변수를 가진 시스템을 모델링하는 데 사용됩니다.이것이 항상 대칭 파괴를 수반하는 다른 위상 천이로부터 그것들을 특이하게 만드는 것입니다.XY 모델의 위상 결함은 저온 단계에서 고온 무질서 단계로 소용돌이 결합 해제 전환으로 이어집니다.실제로, 두 가지 조건 모두 M(β) = 0임에도 불구하고, 고온에서는 기하급수적으로 빠르게 붕괴하는 반면, 낮은 온도에서는 멱함수 법칙과 함께 붕괴한다는 사실을 코스테리츠라고 한다.투울리스 천이군요.코스테를리츠와 툴레스는 왜 그런지에 대한 간단한 논거를 제시했는데, 이것은 하나의 소용돌이를 더하여 모든 스핀이 같은 방향으로 구성되어 있는 지면 상태를 고려한 것이다.이들 존재는 대략 S ln ( L / )(\ S의 엔트로피를 기여한다. 서\a는 이산 격자의 유효 길이 척도이다.양 E J ln / ) { E=\ J 이들을 종합하면, 소용돌이의 자연 형성에 의해 계의 자유 에너지가 변화한다.
Ising 모델을 시각화하려면 위쪽 또는 아래쪽을 가리키는 화살표를 사용하거나 검은색/흰색으로 표시된 점을 사용하여 모델을 표시할 수 있습니다.XY 스핀 시스템을 시각화하기 위해 스핀은 특정 방향을 가리키는 화살표로 나타내거나 특정 색상의 점으로 나타낼 수 있습니다.여기서는 각각의 가능한 연속변수로 인해 다양한 색상으로 스핀을 표현할 필요가 있다.예를 들어 연속적이고 주기적인 적-녹-청 스펙트럼을 사용하여 이를 수행할 수 있다.그림과 같이 청록색은 0도 각도(오른쪽을 가리킴)에 해당하는 반면, 빨간색은 180도 각도(왼쪽을 가리킴)에 해당합니다.그런 다음 서로 다른 온도에서 스핀 구성의 스냅샷을 연구하여 XY 모델의 임계 온도 이상과 이하에서 발생하는 현상을 설명할 수 있습니다.고온에서는 에너지적으로 유리한 구성이 선호되지 않기 때문에 스핀의 방향이 선호되지 않으며 인접한 스핀 간에 예측 불가능한 각도 변화가 발생합니다.이 경우 컬러 맵은 매우 화소화되어 보입니다.한편, 저온에서는, 1개의 가능한 지면 상태 구성이, 모든 스핀이 같은 방향(동일한 각도)을 가리키고 있습니다.이것은, 모든 스핀이 거의 같은 색을 가지는 칼라 맵의 영역(도메인)에 대응합니다.
코스테리츠의 결과로 존재하는 소용돌이(또는 항피질제)를 식별한다.툴리스 천이는 시계 반대 방향으로 격자점들의 원을 가로지르는 것으로 각도의 부호 변화를 결정할 수 있다.각도의 총 변화가 0인 경우 이는 소용돌이가 존재하지 않는 것에 해당하지만 ± \\pi각도의 총 변화는 소용돌이(또는 대피질)에 해당합니다.이 소용돌이는 위상적으로 중요하지 않은 물체입니다. 소용돌이와 대피질의 쌍으로 이루어져 분리되거나 쌍으로 소멸될 수 있습니다.콜로맵에서 이러한 결함은 스펙트럼의 모든 색상이 점 주위에서 만나는 큰 색 구배가 있는 영역에서 확인할 수 있습니다.질적으로 이러한 결함은 흐름의 내향 또는 외향 소스, 집합적으로 시계방향 또는 반시계방향으로 향하는 스핀의 소용돌이, 또는 일부 스핀이 결함에서 멀어지는 쌍곡선처럼 보일 수 있다.긴 시간 척도와 낮은 온도에서 구성이 연구됨에 따라, 이러한 소용돌이-대피질 쌍 중 많은 쌍이 서로 더 가까워지고 결국 쌍-안니힐레이트되는 것이 관찰됩니다.이러한 소용돌이와 항피질제가 서로 분리되고 결합이 풀리는 것은 고온에서만 가능합니다.
연속 XY 모델에서는 고온 자연 자화가 사라집니다.
McBryan과 Spencer가 상한을 찾은 동안, 임의의 > \ > }에 대해
3차원 이상
상호작용의 범위와는 무관하게 충분히 낮은 온도에서 자화는 양입니다.
- 고온에서는 (β) : i (\ M (\ ) : \ ). 또한 클러스터 팽창은 스핀 상관 클러스터가 기하급수적으로 빠른 것으로 나타납니다. 예를 들어 s s s βj C
- 낮은 온도에서, 적외선 범위에서 자연 발생 자기화 엄격하게 긍정적:M(β):\s⟨ 나는 을 ⟩;0{\displaystyle M(\beta):)\langle \mathbf{s}_{나는}\rangle<>를 사용하여 0}일 경우. 이외에도 극값의 국가들이1-parameter 가족, ⟨⋅⟩ θ{\displaystyle \langle.\cdot\;\rangle ^{\theta}}존재한다. , such si ( ) ( 、 )) ) _ \ { { } \ ^ { \ } =( \ \ , \ \ ) } ,,,, extremationsations decayurally,,, icallyicallyicallyicallyicallyicallyicallyicallyicallyicallyically theicallyicallyically the the the the algebra algebra algebra algebra algebra algebra algebra algebra algebra algebra algebra algebra{{{{ algebra algebra algebra algebra algebra algebra algebra
상전이
위에서 언급한 것처럼 XY 모델은 위상 전이가 없는 반면, 2차원에서는 지수 상관 함수와 멱함수 붕괴 상관 함수가 있는 위상 간에 Berezinski-Kosterlitz-Thouless 전이가 있습니다.
XY 모델은 3차원 이상에서 강자석-패러마그넷 상전이 있습니다.저온에서 자연 자화는 0이 아닙니다. 이것이 강자성상입니다.온도가 상승함에 따라 자연 자화는 임계 온도에서 점차 감소하여 사라진다.고온에서는 모두 제로로 남습니다.이것은 상사성 단계입니다.
4차원 이상에서 위상 천이는 평균 필드 이론 임계 지수를 가집니다(4차원의 로그 보정 포함).
3차원 케이스: 임계 지수
3차원 사례는 위상 전이 시 임계 지수가 중요하지 않기 때문에 흥미롭다.많은 3차원 물리적 시스템은 3차원 XY 모델과 동일한 보편성 클래스에 속하며 동일한 임계 지수, 특히 쉬운 평면 자석과 액체 헬륨-4를 공유합니다.이러한 임계 지수의 값은 실험, 몬테카를로 시뮬레이션에 의해 측정되며, 또한 재규격화 그룹 및 등가 부트스트랩과 같은 양자장 이론의 이론적 방법에 의해 계산될 수 있다.XY 모델의 임계점은 재규격화 그룹 고정점에 의해 설명된다고 생각되므로 재규격화 그룹 방법이 적용됩니다.컨포멀 부트스트랩 방식은 유니터리 3차원 컨포멀 필드 이론으로도 간주되기 때문에 적용할 수 있습니다.
3차원 XY 모델의 가장 중요한 중요 지수는 β,, β, β, ,, {\, \, \eta 입니다.모두 스케일링 치수 ϕ \ style \ _ and and and and and and and and and and and and and and r 파라미터 및 선두 싱글트 "\ s (긴즈부르크-란다우 설명의 " ^{ 와 동일)또 다른 중요한 분야는 치러′{s\displaystyle'}(ϕ 4{\displaystyle\phi ^{4} 같은})의 차원Δ s′{\displaystyle \Delta_{s'}}. computation,[14]이 세차원이 있는 giv 정각의 부트 스트랩에 따르면correction-to-scaling 지수ω{\displaystyle \omega}을 결정한다.en기준:
| 0.519088(22) | |
| 1.51136(22) | |
| 3.794(8) |
이를 통해 다음과 같은 임계 지수 값이 제공됩니다.
| 일반식 ( { d ) | 수치 | |
|---|---|---|
| α | -0.01526(30) | |
| β | 0.34869(7) | |
| γ | 1.3179(2) | |
| δ | 4.77937(25) | |
| η | 0.038176(44) | |
| ν | 0.67175(10) | |
| ω | 0.794(8) |
Monte Carlo 메서드는 호환 [15]가능한 결정을 제공합니다. ) 、 0. )、 )\ \=0 ) \ nu ) \
「 」를 참조해 주세요.
메모들
- ^ Stanley, H.E. (1968). "Dependence of Critical Properties on Dimensionality of Spins". Phys. Rev. Lett. 20 (12): 589–592. Bibcode:1968PhRvL..20..589S. doi:10.1103/PhysRevLett.20.589.
- ^ Chaikin, P.M.; Lubensky, T.C. (2000). Principles of Condensed Matter Physics. Cambridge University Press. ISBN 978-0521794503.
- ^ Ginibre, J. (1970). "General formulation of Griffiths' inequalities". Comm. Math. Phys. 16 (4): 310–328. Bibcode:1970CMaPh..16..310G. doi:10.1007/BF01646537. S2CID 120649586.
- ^ Aizenman, M.; Simon, B. (1980). "A comparison of plane rotor and Ising models". Phys. Lett. A. 76 (3–4): 281–282. Bibcode:1980PhLA...76..281A. doi:10.1016/0375-9601(80)90493-4.
- ^ Badalian, D. (1996). "On the thermodynamics of classical spins with isotrop Heisenberg interaction in one-dimensional quasi-periodic structures". Physica B. 226 (4): 385–390. Bibcode:1996PhyB..226..385B. doi:10.1016/0921-4526(96)00283-9.
- ^ Mattis, D.C. (1984). "Transfer matrix in plane-rotator model". Phys. Lett. 104 A (6–7): 357–360. Bibcode:1984PhLA..104..357M. doi:10.1016/0375-9601(84)90816-8.
- ^ Mattis, D. C. (1985). The Theory of Magnetism II. Springer Series in Solid-State Physics. ISBN 978-3-642-82405-0.
- ^ Ota, S.; Ota, S.B.; Fahnle, M (1992). "Microcanonical Monte Carlo simulations for the two-dimensional XY model". J. Phys.: Condens. Matter. 4 (24): 5411. Bibcode:1992JPCM....4.5411O. doi:10.1088/0953-8984/4/24/011.
- ^ Hsieh, Y.-D.; Kao, Y.-J.; Sandvik, A.W. (2013). "Finite-size scaling method for the Berezinskii-Kosterlitz-Thouless transition". Journal of Statistical Mechanics: Theory and Experiment. 2013 (9): P09001. arXiv:1302.2900. Bibcode:2013JSMTE..09..001H. doi:10.1088/1742-5468/2013/09/P09001. S2CID 118609225.
- ^ Nguyen, P.H.; Boninsegni, M. (2021). "Superfluid Transition and Specific Heat of the 2D x-y Model". Appl. Sci. 11 (11): 4931(8). doi:10.3390/app11114931.
- ^ Tobochnik, J.; Chester, G.V. (1979). "Monte Carlo study of the planar spin model". Phys. Rev. B. 20 (9): 3761–3769. Bibcode:1979PhRvB..20.3761T. doi:10.1103/PhysRevB.20.3761.
- ^ Binder, K. (2013). Applications of the Monte Carlo Method in Statistical Physics. Springer Science & Business Media. ISBN 978-3-642-51703-7.
- ^ Fröhlich, J.; Spencer, T. (1981). "The Kosterlitz–Thouless transition in two-dimensional abelian spin systems and the Coulomb gas". Comm. Math. Phys. 81 (4): 527–602. Bibcode:1981CMaPh..81..527F. doi:10.1007/bf01208273. S2CID 73555642.
- ^ Chester, Shai M.; Landry, Walter; Liu, Junyu; Poland, David; Simmons-Duffin, David; Su, Ning; Vichi, Alessandro (2020). "Carving out OPE space and precise O(2) model critical exponents". Journal of High Energy Physics. 2020 (6): 142. arXiv:1912.03324. Bibcode:2020JHEP...06..142C. doi:10.1007/JHEP06(2020)142. ISSN 1029-8479. S2CID 208910721.
- ^ Hasenbusch, Martin (2019-12-26). "Monte Carlo study of an improved clock model in three dimensions". Physical Review B. 100 (22): 224517. arXiv:1910.05916. Bibcode:2019PhRvB.100v4517H. doi:10.1103/PhysRevB.100.224517. ISSN 2469-9950. S2CID 204509042.
레퍼런스
- Evgeny Demidov, XY 모델의 Vortices(2004)
추가 정보
- H. E. 스탠리, 위상 전이 및 임계 현상 입문(Oxford University Press, Oxford and New York 1971)
- H. 클라이너트, 응축 물질의 게이지 필드, Vol. I, "SUPERFLOW AND Voltex LINE", 페이지 1~742, Vol.II, "스트레스와 결함", 743-1456, World Scientific(싱가포르, 1989), Paperback ISBN 9971-5-0210-0(온라인: Vol. I와 Vol. II)


![{\displaystyle P(\mathbf {s} )={\frac {e^{-\beta H(\mathbf {s} )}}{Z}}\qquad Z=\int _{[-\pi ,\pi ]^{\Lambda }}\prod _{j\in \Lambda }d\theta _{j}\;e^{-\beta H(\mathbf {s} )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71ef5f2950de7a5f4eb1d1eacee3cd891b7ea028)



![{\displaystyle H(\mathbf {s} )=-J[\cos(\theta _{1}-\theta _{2})+\cdots +\cos(\theta _{L-1}-\theta _{L})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c073664bcdcef4270af90ece05425114d25b43c)

![{\displaystyle {\begin{aligned}Z&=\int _{-\pi }^{\pi }d\theta _{1}\cdots d\theta _{L}\;e^{\beta J\cos(\theta _{1}-\theta _{2})}\cdots e^{\beta J\cos(\theta _{L-1}-\theta _{L})}\\&=2\pi \prod _{j=2}^{L}\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}=(2\pi )\left[\int _{-\pi }^{\pi }d\theta '_{j}\;e^{\beta J\cos \theta '_{j}}\right]^{L-1}=(2\pi )^{L}(I_{0}(\beta J))^{L-1}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75a41062f2bd4551ebe2affdddaed54033d95f2f)
 첫 번째 유형의
첫 번째 유형의 
![{\displaystyle f(\beta ,h=0)=-\lim _{L\to \infty }{\frac {1}{\beta L}}\ln Z=-{\frac {1}{\beta }}\ln[2\pi I_{0}(\beta J)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fef0b98102ed3e9d32986fb1205efd82c47936c3)


 단거리 상관 함수입니다.
단거리 상관 함수입니다. 







![{\displaystyle Z=[2\pi I_{0}(\beta J)]^{L}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/888ecca89dd7e964668cafd70f8c1da8756baf56)

 제로 필드의 시스템에 대한 섭동으로 취급할 수 있을 정도로 작을 경우
제로 필드의 시스템에 대한 섭동으로 취급할 수 있을 정도로 작을 경우  추정할 수 있습니다.이는 전달 행렬 접근법에 의해 계산된 고유 상태를 사용하고 2차
추정할 수 있습니다.이는 전달 행렬 접근법에 의해 계산된 고유 상태를 사용하고 2차 








 변화합니다.음의 경우 알고리즘은 각도 변화를 받아들이고 양의 경우 에너지 변화에 대한
변화합니다.음의 경우 알고리즘은 각도 변화를 받아들이고 양의 경우 에너지 변화에 대한 





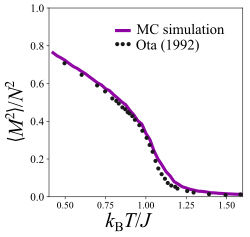
 스핀 수입니다.평균 자화는 시스템의 순 자기 모멘트의 크기를 나타냅니다. 많은 자기 시스템에서는 임계 온도 이상에서 0이 되며 저온에서는 자연스럽게 0이 아닙니다.마찬가지로 평균 제곱 자화는 격자를 가로지르는 스핀의 순 성분 제곱의 평균을 나타냅니다.이들 중 하나는 일반적으로 시스템의 순서 매개변수를 특성화하는 데 사용됩니다.XY 모델의 엄밀한 분석 결과, 열역학 한계에서의 자화는 제로이며, 정사각형 자화는
스핀 수입니다.평균 자화는 시스템의 순 자기 모멘트의 크기를 나타냅니다. 많은 자기 시스템에서는 임계 온도 이상에서 0이 되며 저온에서는 자연스럽게 0이 아닙니다.마찬가지로 평균 제곱 자화는 격자를 가로지르는 스핀의 순 성분 제곱의 평균을 나타냅니다.이들 중 하나는 일반적으로 시스템의 순서 매개변수를 특성화하는 데 사용됩니다.XY 모델의 엄밀한 분석 결과, 열역학 한계에서의 자화는 제로이며, 정사각형 자화는 





















 .모두 스케일링 치수
.모두 스케일링 치수