축류

유사 벡터 또는 키랄 전류로도 표시되는 축 전류는 시스템의 키랄 대칭 또는 축 대칭과 관련된 보존 전류입니다.

기원.

Noether의 정리에 따르면, 시스템의 각 대칭은 보존된 ^[1]^[2]양과 관련이 있습니다.예를 들어, 시스템의 회전 불변성은 각운동량의 보존을 의미하거나 시공간 불변성은 에너지-운동량의 보존을 의미합니다.양자장 이론에서, 내부 대칭은 또한 보존된 양을 초래합니다.예를 들어, QED의 U(1) 게이지 변환은 전하의 보존을 의미합니다.마찬가지로, 만약 어떤 이론이 내부 키랄 또는 축 대칭을 가지고 있다면, 축 전하라고 불리는 보존된 양이 있을 것입니다.또한, 대전된 입자의 움직임이 전류를 생성하는 것처럼, 이동하는 축방향 전하는 축방향 전류를 구성합니다.

정의.

축방향으로 대전된 움직이는 입자의 움직임에 따른 축방향 전류는 공식적으로 j $j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi$ $j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi$ $=$ $j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi$ 5 $ψ$ \ $displaystyle j_{5}^{\mu$ } = $j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi$ }\ $^{\mu$ }\ psi로 $정의$ 됩니다 $j_{5}^{\mu }={\overline {\psi }}\gamma ^{5}\gamma ^{\mu }\psi$ 여기서 $\psi$ γ ${\displaystyle$ \psi $}$ 는 $\psi$ (입자가 일반적으로 스핀-1/2 페르미온이기 때문에) 디랙 스피너로 표현되는 입자 필드이고, $\gamma ^{\mu }$ 5 ${{\$ ^{ $5$ 와 γ ${{{\$ ^{\ $mu$ }}는 디랙 감마 ^[3]행렬입니다.

비교를 위해, 전하를 띤 움직이는 입자에 의해 생성되는 전자기 전류는 j $j^{\mu }={\overline {\psi }}\gamma ^{\mu }\psi$ $=$ $j^{\mu }={\overline {\psi }}\gamma ^{\mu }\psi$ $γ$ μ $j^{\mu }={\overline {\psi }}\gamma ^{\mu }\psi$ ψ \ $displaystyle$ j $^{\mu$ } = $j^{\mu }={\overline {\psi }}\gamma ^{\mu }\psi$ ^{\mu $}\psi$ 입니다.

의미.

위에서 설명한 바와 같이 축 전류는 U(1) 대칭이 아닌 축 대칭에 대한 전자기 전류와 동일합니다.또 $\psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}$ 다른 관점은 키랄 대칭이 필드 회전 하에서 이론의 불변성이라는 것을 상기함으로써 제공됩니다. $\psi _{\rm {R}}\rightarrow \psi _{\rm {R}}$ L $\psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}$ $\psi _{\rm {R}}\rightarrow \psi _{\rm {R}}$ $\psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}$ $\psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}$ L $\psi _{\rm {L}}\rightarrow e^{i\theta _{\rm {L}}}\psi _{\rm {L}}$ ψ L \ $displaystyle \psi$ _ ${\$ $rm$ { $L$ $}}\rightarrow$ e $^{i\theta$ _ ${\$ $rm$ { $L$ $}}}\$ $psi$ $\psi _{\rm {R}}\rightarrow \psi _{\rm {R}}$ → $ψ$ R $\$ $rm {\rightpsi$ \ $rm$ \ $rm}$ ${R}}($ 또는 $\psi _{\rm {L}}\rightarrow \psi _{\rm {L}}$ $\psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}$ L $\psi _{\rm {L}}\rightarrow \psi _{\rm {L}}$ $\psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}$ $\psi _{\rm {L}}\rightarrow \psi _{\rm {L}}$ $L$ _ ${\rm$ { $L}})$ 및 $\psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}$ R → e ψ R $\psi _{\rm {L}}\rightarrow \psi _{\rm {L}}$ $θ$ R \ $\psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}$ ${\rm {R}\rightarrow^{i\rightarrow^{i\$ rm ${R$ }), $\psi _{\rm {R}}\rightarrow e^{i\theta _{\rm {R}}}\psi _{\rm {R}}$ 여기서 $\psi _{\rm {L}}$ $\psi _{\rm {R}}$ L{\ $displaystyle \psi_{\rm {L}}$ 은 $\psi _{\rm {L}}$ (는) 왼손잡이 필드를 나타내고 $\psi _{\rm {R}}$ R{\ $displaystyle \psi_{\rm {R}}$ 은 $\psi _{\rm {R}}$ (는) 오른손잡이 필드를 나타냅니다.여기에 더하여 $=$ $\psi =\psi _{\rm {L}}+\psi _{\rm {R}}$ L + $\psi =\psi _{\rm {L}}+\psi _{\rm {R}}$ R ${$ =\ $psi$ _ ${\rm$ { $L}}+\psi$ _ ${\rm$ ${$ $R}}$ 와 $\psi =\psi _{\rm {L}}+\psi _{\rm {R}}$ $j_{5}^{\mu }$ 위의 $j_{5}^{\mu }$ 5 $j_{5}^{\mu }$ 의 정의를 보면 축류는 왼손잡이 페르미온에 의한 전류와 오른손잡이에 의한 $전류$ 사이의 차이임을 알 수 있습니다.전자기 전류가 합인 동안.

키랄 대칭은 질량이 없는 페르미온을 가진 벡터 게이지 이론에 의해 나타납니다.자연에 알려진 무질량 페르미온이 없기 때문에 키랄 대칭은 기본 이론에서 기껏해야 대략적인 대칭이며 축 전류는 보존되지 않습니다.(참고: 0이 아닌 질량에 의한 키랄 대칭의 명시적인 깨짐은 강입자 물리학에서 지배적인 역할을 하는 자발적인 키랄 대칭 깨짐과 혼동되어서는 안 됩니다.)이러한 비보존의 중요한 결과는 중성 파이온 붕괴와 파이온 붕괴 ^[5]^[6]폭과 직접적인 관련이 있는 키랄 ^[4]이상입니다.

적용들

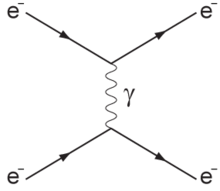
축류는 고에너지 산란 반응을 설명하는 형식주의의 중요한 부분입니다.이러한 반응에서 두 입자는 전자파 산란을 위한 광자와 같은 힘 보손을 교환하여 서로 산란합니다(그림 참조).

가상 광자의 방출에 의해 두 전자 사이에 산란하는 파인만 다이어그램.

그러한 반응에 대한 단면은 산란 진폭의 제곱에 비례하며, 이는 두 충돌 ^[7]입자 운동과 관련된 두 전류와 보손 전파 시간의 곱에 의해 주어집니다.따라서 전류(축 또는 전자기)는 고에너지 산란을 계산하는 데 필요한 두 가지 필수 요소 중 하나이며, 다른 하나는 보손 전파기입니다.

전자-핵자 산란(또는 더 일반적으로 하전 렙톤-하드론/핵자 산란)에서 축류는 ^[8]단면의 스핀 의존적인 부분을 산출합니다.(단면의 스핀 평균 부분은 전자기 ^[7]전류에서 나옵니다.)

중성미자-핵자 산란에서 중성미자는 축류를 통해서만 결합하므로 전하를 띤 ^[9]렙톤과는 다른 핵자 구조 정보에 접근합니다.

중성 파이온은 또한 파이온이 유사 스칼라 입자이기 때문에 축 전류를 통해서만 결합하고 진폭(스칼라 양)을 생성하려면 파이온이 축 전류와 같은 다른 유사 스칼라 물체에 결합해야 합니다. (충전된 파이온도 전자 전류를 통해 결합할 수 있습니다.)

참고 항목

레퍼런스

^ Byers, Nina (1998). "E. Noether's Discovery of the Deep Connection Between Symmetries and Conservation Laws". arXiv:physics/9807044.
^ Baez, John (2002). "Noether's Theorem in a Nutshell". math.ucr.edu. Retrieved 28 August 2020.
^ Zee, A. (2010-02-01). Quantum Field Theory in a Nutshell: Second Edition. Princeton University Press. p. 100. ISBN 978-1-4008-3532-4.
^ Dolgov, A. D. (1997). "Baryogenesis, 30 years after". Surveys in High Energy Physics. 13 (1–3): 83–117. arXiv:hep-ph/9707419. Bibcode:1998SHEP...13...83D. doi:10.1080/01422419808240874. S2CID 119499400.
^ Adler, S. L. (1969). "Axial-Vector Vertex in Spinor Electrodynamics". Physical Review. 177 (5): 2426–2438. Bibcode:1969PhRv..177.2426A. doi:10.1103/PhysRev.177.2426.
^ Bell, J. S.; Jackiw, R. (1969). "A PCAC puzzle: π⁰→γγ in the σ-model". Il Nuovo Cimento A. 60 (1): 47–61. Bibcode:1969NCimA..60...47B. doi:10.1007/BF02823296. S2CID 125028356.
^ ^a ^b Peskin, M.; Schroeder, D. (1995). An Introduction to Quantum Field Theory. Westview Press. ISBN 978-0-201-50397-5.
^ A. Deur, S. J. Brodsky, G. F. de Teramond (2019) "핵자의 스핀 구조" 파충류.프로그램. 물리학.82 076201
^ Zuber, K. (2003). Neutrino Physics. IOP Publishing. ISBN 978-0-7503-0750-5.

[1] Byers, Nina (1998). "E. Noether's Discovery of the Deep Connection Between Symmetries and Conservation Laws". arXiv:physics/9807044.

[2] Baez, John (2002). "Noether's Theorem in a Nutshell". math.ucr.edu. Retrieved 28 August 2020.

[3] Zee, A. (2010-02-01). Quantum Field Theory in a Nutshell: Second Edition. Princeton University Press. p. 100. ISBN 978-1-4008-3532-4.

[4] Dolgov, A. D. (1997). "Baryogenesis, 30 years after". Surveys in High Energy Physics. 13 (1–3): 83–117. arXiv:hep-ph/9707419. Bibcode:1998SHEP...13...83D. doi:10.1080/01422419808240874. S2CID 119499400.

[Adler-5] Adler, S. L. (1969). "Axial-Vector Vertex in Spinor Electrodynamics". Physical Review. 177 (5): 2426–2438. Bibcode:1969PhRv..177.2426A. doi:10.1103/PhysRev.177.2426.

[bj-6] Bell, J. S.; Jackiw, R. (1969). "A PCAC puzzle: π⁰→γγ in the σ-model". Il Nuovo Cimento A. 60 (1): 47–61. Bibcode:1969NCimA..60...47B. doi:10.1007/BF02823296. S2CID 125028356.

[peskin-7] Peskin, M.; Schroeder, D. (1995). An Introduction to Quantum Field Theory. Westview Press. ISBN 978-0-201-50397-5.

[SR_review-8] A. Deur, S. J. Brodsky, G. F. de Teramond (2019) "핵자의 스핀 구조" 파충류.프로그램. 물리학.82 076201

[Zuber-9] Zuber, K. (2003). Neutrino Physics. IOP Publishing. ISBN 978-0-7503-0750-5.

[1]

[2]

[3]

[5]

[6]

[4]

[7]

[8]

[9]

Search

축류

네임스페이스

더

목차

기원.

정의.

의미.

적용들

참고 항목

레퍼런스