감도 및 특이성
Sensitivity and specificity민감도와 특수성은 조건의 유무를 보고하는 검정의 정확성을 수학적으로 기술합니다.조건이 충족된 개인은 "긍정적"으로 간주되고, 그렇지 않은 개인은 "부정적"으로 간주됩니다.
- 감도(진정한 양성 비율)는 진정 양성을 조건으로 하는 양성 검정의 확률을 나타냅니다.
- 특이성(참 음수 비율)은 음수가 되는 것을 조건으로 하는 음수 검정의 확률을 나타냅니다.
실제 조건을 알 수 없는 경우 "골드 표준 테스트"가 올바른 것으로 가정합니다.진단 검정의 감도는 검정이 참 양성을 얼마나 잘 식별할 수 있는지를 나타내는 척도이며, 특수성은 검정이 참 음성을 얼마나 잘 식별할 수 있는지를 나타내는 척도입니다.모든 테스트(진단 및 스크리닝)에 대해 일반적으로 민감도와 특이성 사이에 트레이드오프가 있기 때문에 높은 민감도는 낮은 특이성을 의미하며 그 반대도 마찬가지이다.
만약 이 검사의 목적이 질환이 있는 모든 사람을 식별하는 것이라면, 거짓 음성 수치는 낮아야 하며, 이것은 높은 민감도를 필요로 한다.즉, 이 질환이 있는 사람은 테스트에 의해 식별될 가능성이 매우 높아야 한다.이는 질환 치료 실패의 결과가 심각하거나 치료가 매우 효과적이고 부작용이 최소인 경우에 특히 중요하다.
만약 이 검사의 목적이 질환이 없는 사람을 정확하게 식별하는 것이라면, 거짓 양성자의 수는 매우 낮아야 하며, 이것은 높은 특수성을 필요로 한다.즉, 조건을 갖추지 않은 사람은 검사에서 제외될 가능성이 매우 높습니다.이는 특히 질환이 있는 것으로 확인된 사람들이 더 많은 검사, 비용, 낙인, 불안 등을 받을 수 있는 경우에 중요합니다.
민감성과 특이성이라는 [1]용어는 1947년 미국의 생물학자 제이콥 예루샬미에 의해 도입되었다.
출처:포싯(2006년),[2] 피료네시와 엘-디라비(2020년),[3] 파워스([4]2011년), [5]팅(2011년), CAWCR,[6] D. 치코&G. 주르만(2020년,[7][8] 2021년), 타르와트(2018년).[9] |
스크리닝 스터디에 적용
질병을 검사하는 검사를 평가하는 연구를 상상해 보십시오.시험을 보는 사람마다 그 병이 있거나 없거나 둘 중 하나다.검사 결과는 양성(질병에 걸린 것으로 분류) 또는 음성(질병에 걸리지 않은 것으로 분류)일 수 있습니다.각 피험자의 테스트 결과는 피험자의 실제 상태와 일치하거나 일치하지 않을 수 있습니다.이 설정에서는:
- 진정한 긍정:아픈 사람이 아픈 것으로 올바르게 식별됨
- 잘못된 긍정:건강한 사람이 병으로 잘못 식별됨
- True Negative(진정한 부정):건강한 사람이 건강한 것으로 올바르게 식별됨
- 거짓 부정:건강한 것으로 잘못 식별된 환자
참 긍정, 거짓 긍정, 참 부정 및 거짓 부정의 수를 얻은 후 테스트의 민감도와 특이도를 계산할 수 있습니다.민감도가 높은 것으로 판명되면, 그 병에 걸린 사람은 검사에서 양성으로 분류될 가능성이 높습니다.반면 특이성이 높으면 그 병에 걸리지 않은 사람은 검사에서 음성으로 분류될 가능성이 높다.NIH 웹사이트에서는 이들 비율이 어떻게 [10]계산되는지에 대해 논의하고 있습니다.
정의.
감도
상태를 진단하기 위한 의료 검사의 예를 생각해 보십시오.민감도는 그 [11]상태를 가진 아픈 환자들을 정확하게 발견할 수 있는 테스트의 능력을 말한다.상태를 식별하는 데 사용되는 의료 검사의 예에서 검사의 민감도(임상 환경에서 검출률이라고도 함)는 질병을 가진 사람 중 질병에 대해 양성 반응을 보이는 사람의 비율이다.이는 수학적으로 다음과 같이 나타낼 수 있습니다.
감도가 높은 검사에서 음성 결과가 나오면 질병을 [11]배제하는 데 도움이 됩니다.고감도 검사는 환자 오진을 거의 하지 않기 때문에 음성일 때 신뢰성이 높다.100% 민감도 검사는 양성 반응을 통해 모든 환자를 인식합니다.음성 검사 결과는 환자에게서 질병의 존재를 분명히 배제할 것이다.그러나 고감도 검사에서 양성 반응이 나온다고 해서 반드시 질병 판정에 도움이 되는 것은 아니다.'보거스' 테스트 키트가 항상 양의 판독값을 제공하도록 설계되었다고 가정합니다.병든 환자에게 사용할 경우 모든 환자가 양성 반응을 보여 100% 민감도를 보입니다.단, 감도는 false positive는 고려하지 않습니다.이 가짜 테스트는 또한 모든 건강한 환자들에게 양성으로 나타나 100%의 잘못된 양성률을 주며, 질병을 발견하거나 "결정"하는 데 무용지물이 됩니다.
민감도 계산에는 불확실한 검사 결과는 고려되지 않습니다.테스트를 반복할 수 없는 경우, 불확정 표본은 분석에서 제외되거나(감도를 인용할 때 제외 수를 명시해야 함) 거짓 음성으로 취급될 수 있다(감도에 대한 최악의 경우 값을 제공하므로 과소평가할 수 있음).
특이성
질병 진단을 위한 의료 검사의 예를 생각해 보십시오.특이성은 조건 없이 건강한 환자를 정확하게 거부할 수 있는 테스트 능력과 관련이 있습니다.검정의 특수성은 해당 조건에 대해 음성을 검정하는 실제로 조건을 가지고 있지 않은 사람의 비율입니다.수학적으로 이것은 다음과 같이 쓸 수도 있습니다.
특이성이 높은 검사에서 양성 반응이 나오면 질병 판정에 도움이 됩니다.그 검사는 건강한 환자들에게 양성 반응을 보이는 경우는 거의 없다.양성 결과는 [12]질병이 존재할 가능성이 높다는 것을 의미합니다.100% 특이성 검사는 음성 검사를 통해 질병이 없는 모든 환자를 인식하기 때문에 양성 검사 결과는 반드시 질병 유무에서 판정됩니다.그러나 높은 특이성 검사에서 음성 결과가 반드시 질병을 배제하는 데 도움이 되는 것은 아닙니다.예를 들어, 항상 음성 검사 결과를 반환하는 검정의 특수성은 거짓 음성을 고려하지 않으므로 100%의 특수성을 가집니다.그런 검사는 환자들에게 음성으로 돌아오기 때문에 질병을 배제하는 데 도움이 되지 않는다.
그래픽스 일러스트
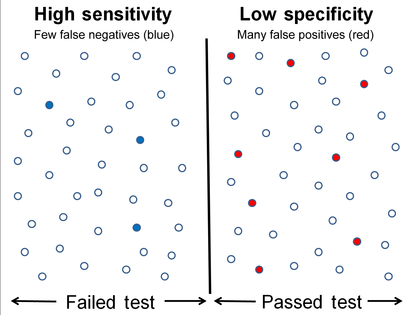
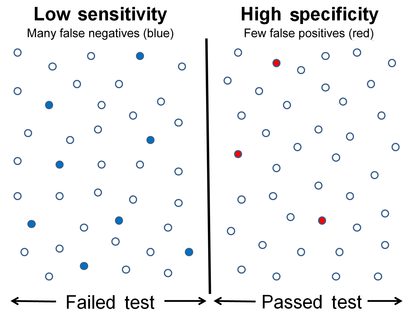
위의 그래픽 그림은 민감도와 특수성 사이의 관계를 보여주기 위한 것입니다.그래프 중앙에 있는 검은색 점선은 감도와 특이도가 동일한 부분입니다.검은 점선의 왼쪽으로 이동하면 감도가 증가하여 A선에서 최대값인 100%에 도달하고 특이도가 감소합니다.라인 A의 감도는 100%입니다. 왜냐하면 이 시점에는 잘못된 음이 0개 있기 때문입니다. 즉, 모든 음의 검정 결과가 참 음이 됩니다.오른쪽으로 이동하면 반대로 B 라인에 도달하여 100%가 될 때까지 특이도가 증가하고 감도가 감소합니다.라인 B에서는 폴스 포지티브의 수가 0이기 때문에, 라인 B의 특이성은 100%입니다.이는 모든 양성 테스트 결과가 참 양성임을 의미합니다.
두 그림에서 감도와 특이성의 수준을 나타내는 중간 실선은 테스트 컷오프 포인트입니다.이 선을 이동하면 앞서 설명한 민감도와 특수성 수준 간에 트레이드오프가 발생한다.이 선의 왼쪽에는 조건이 있는 데이터 포인트가 포함되어 있습니다(파란색 점은 잘못된 음수를 나타냅니다).선의 오른쪽에는 조건이 없는 데이터 포인트가 표시됩니다(빨간색 점은 false positive를 나타냅니다).데이터 포인트의 총수는 80개입니다.그 중 40개는 병세가 있고 왼쪽에 있습니다.나머지는 우측에 있고 의학적 상태는 아닙니다.
고감도 및 저특이도를 나타내는 수치는 거짓 음수 3개, 의료 조건을 가진 데이터 포인트 수 40개이므로 민감도는 (40 - 3) / (37 + 3) = 92.5%이다.잘못된 긍정의 수는 9이므로 특수성은 (40 - 9) / 40 = 77.5%입니다.마찬가지로, 다른 그림에서 거짓 음성의 수는 8이고, 의료 조건을 가진 데이터 지점의 수는 40이므로 민감도는 (40 - 8) / (37 + 3) = 80%이다.잘못된 긍정의 수는 3이므로 특수성은 (40 - 3) / 40 = 92.5%입니다.
빨간색 점은 의료 상태가 있는 환자를 나타냅니다.빨간색 배경은 검정에서 데이터 점이 양수일 것으로 예측되는 영역을 나타냅니다.이 그림에서 진정한 양의 값은 6이고 잘못된 음의 값은 0입니다(모든 양의 조건이 양으로 올바르게 예측되기 때문입니다).따라서 감도는 100%(6 / (6 + 0)입니다.이 상황은 점선이 위치 A에 있는 이전 그림에도 나타나 있습니다(왼쪽은 모델에 의해 음으로 예측되고 오른쪽은 모델에 의해 양으로 예측됨).점선, 검정 컷오프 선이 위치 A에 있으면 검정에서는 참 양수 클래스의 모든 모집단을 올바르게 예측하지만 참 음수 클래스의 데이터 점을 올바르게 식별하지 못합니다.
앞서 설명한 그림과 마찬가지로 빨간색 점은 의학적 상태가 있는 환자를 나타냅니다.그러나 이 경우 녹색 배경은 검사에서 모든 환자가 의학적 상태를 벗어났음을 나타냅니다.그러면 참 음수인 데이터 포인트의 수는 26이 되고 거짓 긍정의 수는 0이 됩니다.그 결과 특이성이 100%가 됩니다(26 / (26 + 0)).따라서 민감도 또는 특이성만으로는 테스트 성능을 측정할 수 없습니다.
의료용
의료 진단에서 테스트 민감도는 질병이 있는 사람을 정확하게 식별하는 테스트 능력(진정한 양성률)인 반면, 테스트 특이성은 질병이 없는 사람을 정확하게 식별하는 테스트 능력(진정한 음성률)이다.질병이 있는 것으로 알려진 100명의 환자를 검사하고 43명의 환자가 양성 반응을 보인 경우 검사의 민감도는 43%입니다.질병이 없는 100을 검사하고 96이 완전히 음성 결과를 반환하면 검사의 특이성은 96%입니다.민감도와 특이성은 해당 값이 시험에 고유하며 관심 [13]모집단의 질병 유병률에 의존하지 않기 때문에 유병률에 의존하지 않는 검사 특성이다.민감도나 특이성이 아닌 양성과 음성의 예측값은 테스트 대상 모집단의 질병 유병률에 의해 영향을 받는 값이다.이러한 개념은 이 애플릿 베이지안 임상 진단 모델에서 그래픽으로 설명되며, 이 모델은 유병률, 민감도 및 특이성의 함수로서 양의 예측 값과 음의 예측 값을 보여준다.
오해
흔히 양성일 경우 특정 검사가 질병 판정에 효과가 있는 반면, [14][15]음성일 경우 민감도가 높은 검사가 질병을 배제하는 데 효과적이라고 주장합니다.이에 따라 널리 사용되는 니모닉 SPPIN과 SNNOUT가 생겨났으며, 이에 따라 양성일 경우 질병(SP-P-IN)에 대한 매우 구체적인 검사(SP-P-IN)가, 음성일 경우 매우 민감한 검사(SN-N-OUT)가 질병을 배제합니다.그러나 두 가지 경험칙은 모두 테스트의 진단력이 [16][17][18]민감도와 특수성 모두에 의해 결정되기 때문에 추정적으로 오해를 불러일으킨다.
특수성과 민감도 사이의 트레이드오프는 TPR과 FPR 사이의 트레이드오프(즉, 리콜과 낙진)로서 [19]ROC 분석에서 탐구된다.동일한 가중치를 부여하면 지식도 = 특이성 + 민감도 - 1 = TPR - FPR을 최적화할 수 있다(> 0은 정보의 적절한 사용을 나타내고, 0은 기회 수준의 성과를 나타내며, < 0은 정보의 [20]왜곡된 사용을 나타낸다).
감도 지수
감도 지수 또는 d (("dee-prime"로 발음됨)는 신호 검출 이론에서 사용되는 통계량입니다.이는 소음 분포의 표준 편차와 비교하여 신호 평균과 소음 분포 간의 분리를 제공합니다.평균 및 표준 를 갖는 정규 분포 신호 및 노이즈의 경우 S(\_ 및N(\ _ 및 N(\ _은 다음과 같이 정의됩니다.
d†의 추정치는 히트 레이트와 폴스 알람 레이트의 측정에서도 확인할 수 있습니다.계산은 다음과 같습니다.
- d440 = Z(히트 레이트) - Z(허위 알람 레이트),[22]
여기서 함수 Z(p), p [ [0, 1]는 누적 가우스 분포의 역수입니다.
ddp는 무차원 통계 정보입니다.d'가 클수록 신호를 더 쉽게 검출할 수 있음을 나타냅니다.
혼란 행렬
민감도, 특이성 및 유사한 용어 간의 관계는 다음 표를 사용하여 이해할 수 있습니다.어떤 조건의 P 양의 인스턴스와 N 개의 음의 인스턴스가 있는 그룹을 고려합니다.4가지 결과는 다음과 같이 2×2 분할표 또는 혼란 행렬과 4가지 결과를 사용하는 여러 가지 지표의 도출으로 공식화할 수 있다.
| 예측 상태 | 출처:[23][24][25][26][27][28][29][30] | ||||
| 총인구 = P + N | 긍정(PP) | 네거티브(PN) | 정보성, 장부 제작자 정보성(BM) = TPR + TNR - 1 | 유병률 임계값(PT) = × - - displaystyle {\ | |
| 플러스(P) | True Positive (TP; 참, 때리다 | False Negative(FN; 거짓 음성), 타입 II 오류입니다. 과소 평가 | True Positive Rate(TPR), 리콜, 감도(SEN), 검출 확률, 적중률, 전력 =TP/P= 1 - FNR | False Negative Rate(FNR; 거짓 네거티브레이트), 미스 레이트 = FN/P= 1 - TPR | |
| 네거티브(N | False Positive(FP; 거짓 긍정), 유형 I 오류, 잘못된 경보, 과대 평가 | True Negative(TN; 트루 네거티브), 정정 거부 | False Positive Rate(FPR; 거짓 양수율), 허위 경보 발생 확률, 탈락 = FP/N= 1 - TNR | True Negative Rate(TNR; 참 마이너스 레이트), 특이성(SPC), 선택성 = TN/N= 1 - FPR | |
| 유병률 = P/P + N | 양의 예측값(PPV), 정확 = TP/PP = 1 - FDR | 허위누락률(FOR) = FN/PN= 1 - NPV | 양의 우도비(LR+) = TPR/FPR | 음우도비(LR-) = FNR/TNR | |
| 정확도(ACC) = TP + TN/P + N | FDR(False Discovery Rate) = FP/PP= 1 - PPV | 음의 예측값(NPV) = TN/PN = 1 - FOR | 마크니스(MK), 델타P(δP) = PPV + NPV - 1 | 진단 승산비(DOR) = LR+/LR- | |
| 균형 정확도(BA) = TPR + TNR/2 | F1 스코어 = PPV × TPR/PPV + TPR = TP/2 TP + FP + FN | Fowlkes – Mallows 색인(FM) = × \ | Matthews 상관 계수(MCC) = × × ×\ \scriptstyle \{\ ×× {\ | 위협 점수(TS), 중요 성공 지수(CSI), 자카드 지수 = TP/TP + FN + FP | |
- 작업 예
- 인구 유병률 1.48%의 장애를 찾기 위해 민감도 67%, 특이도 91%의 진단 테스트를 2030명에게 적용한다.
| 분변잠혈검사 결과 | |||||
| 총인구 (pop.) = 2030 | 테스트 결과 양성 | 검사 결과 음성 | 정밀도(ACC) = (TP + TN) / 팝. = (20 + 1820) / 2030 § 90.64% | F1 스코어 = 2 × 정밀도 × 회수 / 회수 + 회수 § 0.120 | |
| 환자: 대장암 (확인대로) 내시경 검사 중) | 실제. 조건. 긍정의 | True Positive(TP) = 20 (2030 × 1.48% × 67%) | False Negative(FN; 거짓 음성) = 10 (표준×1.48%×(100%~67%) | True Positive Rate(TPR), 리콜, 감도 = TP / (TP + FN) = 20 / (20 + 10) § 66.7% | False Negative Rate(FNR; 거짓 네거티브레이트), 미스레이트 = FN / (TP + FN) = 10 / (20 + 10) § 33.3% |
| 실제. 조건. 아니요. | False Positive(FP) = 180 (139 × (100% - 1.48%) × (100% - 91%) | True Negative(TN) = 1820 (124 × (100 % - 1.48 %) × 91 %) | False Positive Rate(FPR; 거짓 양수율), 탈락, 거짓 경보 발생 가능성 = FP / (FP + TN) = 180 / (180 + 1820) = 9.0% | 특이성, 선택성, 진정한 네거티브 레이트(TNR) = TN / (FP + TN) = 1820 / (180 + 1820) =91% | |
| 유병률 =(TP + FN) / 팝. = (20 + 10) / 2030 § 1.48 % | 양의 예측값(PPV), 정밀도 = TP / (TP + FP) = 20 / (20 + 180) =10 % | 허위누락률(FOR) = FN / (FN + TN) = 10 / (10 + 1820) § 0.55% | 양의 우도비 (LR+) = TPR/FPR = (20 / 30) / (180 / 2000) § 7.41 | 음우도비 (LR−) = FNR/TNR = (10 / 30) / (1820 / 2000) § 0.366 | |
| FDR(False Discovery Rate) = FP / (TP + FP) = 180 / (20 + 180) = 90.0% | 음의 예측값(NPV) = TN / (FN + TN) = 1820 / (10 + 1820) § 99.45% | 진단 승산비(DOR) = LR+/LR- § 20.2 | |||
관련 계산
- 거짓 양수 비율(α) = 유형 I 오류 = 1 - 특이도 = FP / (FP + TN) = 180 / (180 + 1820) = 9%
- 거짓 음수 비율(β) = 유형 II 오류 = 1 - 민감도 = FN / (TP + FN) = 10 / (20 + 10) 33 33 %
- 검정력 = 감도 = 1 - β
- 양의 우도비 = 민감도 / (1 - 특이도) 0 0.67 / (1 - 0.91) 7 7.4
- 음의 우도비 = (1 - 민감도) / 특이도 ( (1 - 0.67) / 0.91 0 0.37
- 유병률 임계값 = T ( - N +) + R- 1 ( P + - ){ PT =frac {TPR1)}++ 0 0.2686 ≈ 26.9%
이 가상의 선별 검사(분비잠혈 검사)는 [a]대장암 환자의 3분의 2(66.7%)를 정확하게 식별했다.불행히도, 유병률을 고려하면 이 가상의 테스트는 높은 거짓 양성률을 가지고 있으며, 무증상인 전체 모집단에서 대장암을 신뢰성 있게 식별하지 못한다(PPV = 10%).
한편, 이 가상의 테스트는 암이 없는 개인(NPV np 99.5%)의 매우 정확한 검출을 보여준다.따라서, 무증상 성인의 일상적인 대장암 검진에 사용될 때, 음성 결과는 위장 증상의 원인에서 암을 배제하거나 대장암 발생을 우려하는 환자를 안심시키는 등 환자와 의사에게 중요한 데이터를 제공합니다.
인용된 민감도 또는 특수성의 오차 추정
민감도 및 특이성 값만으로는 매우 오해의 소지가 있습니다.결과가 거의 없는 실험에 의존하지 않으려면 '최악의 경우' 민감도 또는 특이도를 계산해야 합니다.예를 들어, 특정 테스트는 금본위제에 대해 네 번 테스트하면 100% 감도를 쉽게 나타낼 수 있지만, 좋지 않은 결과를 얻은 금본위제에 대한 단일 추가 테스트는 80%의 감도만을 의미합니다.이를 위한 일반적인 방법은 종종 Wilson 점수 구간을 사용하여 계산되는 이항 비율 신뢰 구간을 기술하는 것입니다.
민감도 및 특이성에 대한 신뢰 구간을 계산하여 올바른 값이 주어진 신뢰 수준(예: 95%)[33]에 있는 값의 범위를 제공할 수 있다.
정보 검색 용어
정보 검색에서 양의 예측 값을 정밀도라고 하고 감도를 호출이라고 합니다.특이성 대 민감성 트레이드오프와 달리, 이러한 척도는 일반적으로 알려지지 않은 실제 음의 수와 무관하며 관련 문서 및 검색된 문서의 실제 수보다 훨씬 크다.실제 부정 대 긍정의 수가 매우 많다는 가정은 다른 [20]응용 프로그램에서는 거의 찾아볼 수 없습니다.
F 점수는 양성 클래스에 대한 검정 수행의 단일 척도로 사용할 수 있습니다.F 점수는 정밀도와 호출의 조화 평균입니다.
통계 가설 테스트의 전통적인 언어에서, 테스트의 민감도는 테스트의 통계적 힘이라고 불리지만, 그 맥락에서의 단어 힘은 현재 맥락에서는 적용되지 않는 더 일반적인 용법을 가지고 있다.기밀 테스트에서는 타입 II 에러가 적어집니다.
「 」를 참조해 주세요.
메모들
레퍼런스
- ^ Yerushalmy J (1947). "Statistical problems in assessing methods of medical diagnosis with special reference to x-ray techniques". Public Health Reports. 62 (2): 1432–39. doi:10.2307/4586294. JSTOR 4586294. PMID 20340527.
- ^ Fawcett, Tom (2006). "An Introduction to ROC Analysis" (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). "Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index". Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512.
- ^ Powers, David M. W. (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). "WWRP/WGNE Joint Working Group on Forecast Verification Research". Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
- ^ Chicco D.; Jurman G. (January 2020). "The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation". BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^ Chicco D.; Toetsch N.; Jurman G. (February 2021). "The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation". BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
- ^ Tharwat A. (August 2018). "Classification assessment methods". Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
- ^ Parikh, Rajul; Mathai, Annie; Parikh, Shefali; Chandra Sekhar, G; Thomas, Ravi (2008). "Understanding and using sensitivity, specificity and predictive values". Indian Journal of Ophthalmology. 56 (1): 45–50. doi:10.4103/0301-4738.37595. PMC 2636062. PMID 18158403.
- ^ a b Altman DG, Bland JM (June 1994). "Diagnostic tests. 1: Sensitivity and specificity". BMJ. 308 (6943): 1552. doi:10.1136/bmj.308.6943.1552. PMC 2540489. PMID 8019315.
- ^ "SpPins and SnNouts". Centre for Evidence Based Medicine (CEBM). Retrieved 26 December 2013.
- ^ Mangrulkar R. "Diagnostic Reasoning I and II". Retrieved 24 January 2012.
- ^ "Evidence-Based Diagnosis". Michigan State University. Archived from the original on 2013-07-06. Retrieved 2013-08-23.
- ^ "Sensitivity and Specificity". Emory University Medical School Evidence Based Medicine course.
- ^ Baron JA (Apr–Jun 1994). "Too bad it isn't true". Medical Decision Making. 14 (2): 107. doi:10.1177/0272989X9401400202. PMID 8028462. S2CID 44505648.
- ^ Boyko EJ (Apr–Jun 1994). "Ruling out or ruling in disease with the most sensitive or specific diagnostic test: short cut or wrong turn?". Medical Decision Making. 14 (2): 175–9. doi:10.1177/0272989X9401400210. PMID 8028470. S2CID 31400167.
- ^ Pewsner D, Battaglia M, Minder C, Marx A, Bucher HC, Egger M (July 2004). "Ruling a diagnosis in or out with "SpPIn" and "SnNOut": a note of caution". BMJ. 329 (7459): 209–13. doi:10.1136/bmj.329.7459.209. PMC 487735. PMID 15271832.
- ^ Fawcett, Tom (2006). "An Introduction to ROC Analysis". Pattern Recognition Letters. 27 (8): 861–874. Bibcode:2006PaReL..27..861F. doi:10.1016/j.patrec.2005.10.010.
- ^ a b Powers, David M. W. (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Gale SD, Perkel DJ (January 2010). "A basal ganglia pathway drives selective auditory responses in songbird dopaminergic neurons via disinhibition". The Journal of Neuroscience. 30 (3): 1027–37. doi:10.1523/JNEUROSCI.3585-09.2010. PMC 2824341. PMID 20089911.
- ^ Macmillan NA, Creelman CD (15 September 2004). Detection Theory: A User's Guide. Psychology Press. p. 7. ISBN 978-1-4106-1114-7.
- ^ Fawcett, Tom (2006). "An Introduction to ROC Analysis" (PDF). Pattern Recognition Letters. 27 (8): 861–874. doi:10.1016/j.patrec.2005.10.010.
- ^ Piryonesi S. Madeh; El-Diraby Tamer E. (2020-03-01). "Data Analytics in Asset Management: Cost-Effective Prediction of the Pavement Condition Index". Journal of Infrastructure Systems. 26 (1): 04019036. doi:10.1061/(ASCE)IS.1943-555X.0000512.
- ^ Powers, David M. W. (2011). "Evaluation: From Precision, Recall and F-Measure to ROC, Informedness, Markedness & Correlation". Journal of Machine Learning Technologies. 2 (1): 37–63.
- ^ Ting, Kai Ming (2011). Sammut, Claude; Webb, Geoffrey I. (eds.). Encyclopedia of machine learning. Springer. doi:10.1007/978-0-387-30164-8. ISBN 978-0-387-30164-8.
- ^ Brooks, Harold; Brown, Barb; Ebert, Beth; Ferro, Chris; Jolliffe, Ian; Koh, Tieh-Yong; Roebber, Paul; Stephenson, David (2015-01-26). "WWRP/WGNE Joint Working Group on Forecast Verification Research". Collaboration for Australian Weather and Climate Research. World Meteorological Organisation. Retrieved 2019-07-17.
- ^ Chicco D, Jurman G (January 2020). "The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation". BMC Genomics. 21 (1): 6-1–6-13. doi:10.1186/s12864-019-6413-7. PMC 6941312. PMID 31898477.
- ^ Chicco D, Toetsch N, Jurman G (February 2021). "The Matthews correlation coefficient (MCC) is more reliable than balanced accuracy, bookmaker informedness, and markedness in two-class confusion matrix evaluation". BioData Mining. 14 (13): 1-22. doi:10.1186/s13040-021-00244-z. PMC 7863449. PMID 33541410.
- ^ Tharwat A. (August 2018). "Classification assessment methods". Applied Computing and Informatics. doi:10.1016/j.aci.2018.08.003.
- ^ Lin, Jennifer S.; Piper, Margaret A.; Perdue, Leslie A.; Rutter, Carolyn M.; Webber, Elizabeth M.; O’Connor, Elizabeth; Smith, Ning; Whitlock, Evelyn P. (21 June 2016). "Screening for Colorectal Cancer". JAMA. 315 (23): 2576–2594. doi:10.1001/jama.2016.3332. ISSN 0098-7484.
- ^ Bénard, Florence; Barkun, Alan N.; Martel, Myriam; Renteln, Daniel von (7 January 2018). "Systematic review of colorectal cancer screening guidelines for average-risk adults: Summarizing the current global recommendations". World Journal of Gastroenterology. 24 (1): 124–138. doi:10.3748/wjg.v24.i1.124. PMC 5757117. PMID 29358889.
- ^ "Diagnostic test online calculator calculates sensitivity, specificity, likelihood ratios and predictive values from a 2x2 table – calculator of confidence intervals for predictive parameters". medcalc.org.
추가 정보
- Altman DG, Bland JM (June 1994). "Diagnostic tests. 1: Sensitivity and specificity". BMJ. 308 (6943): 1552. doi:10.1136/bmj.308.6943.1552. PMC 2540489. PMID 8019315.
- Loong TW (September 2003). "Understanding sensitivity and specificity with the right side of the brain". BMJ. 327 (7417): 716–9. doi:10.1136/bmj.327.7417.716. PMC 200804. PMID 14512479.






















![{\displaystyle {\begin{aligned}{\text{sensitivity}}&={\frac {\text{number of true positives}}{{\text{number of true positives}}+{\text{number of false negatives}}}}\\[8pt]&={\frac {\text{number of true positives}}{\text{total number of sick individuals in population}}}\\[8pt]&={\text{probability of a positive test given that the patient has the disease}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12ec58e26222c7c528150ce69c86e2aa91ddc4c2)
![{\displaystyle {\begin{aligned}{\text{specificity}}&={\frac {\text{number of true negatives}}{{\text{number of true negatives}}+{\text{number of false positives}}}}\\[8pt]&={\frac {\text{number of true negatives}}{\text{total number of well individuals in population}}}\\[8pt]&={\text{probability of a negative test given that the patient is well}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d48cee2cea0745bcc29d228f8c2783e4cb34547c)






 다음과 같이 정의됩니다.
다음과 같이 정의됩니다.





