제2하모닉

두 번째 고조파 생성(Second-harmonic generation, SHG)은 동일한 주파수를 가진 두 광자가 비선형 물질과 상호작용하고 "결합"되어 초기 광자의 두 배의 에너지(주파수의 두 배, 파장의 절반)로 새로운 광자를 생성하는 비선형 광학 프로세스입니다.흥분의 일관성을 보존하는 것입니다.이것은 합-주파수 생성(2개의 광자)의 특별한 경우이며, 더 일반적으로 고조파 생성의 경우입니다.

매질의 2차 비선형 민감성은 SHG를 유발하는 경향을 특징으로 합니다.다른 짝수차 비선형 광학 현상과 마찬가지로 2차 고조파 생성은 반전 대칭을 가진 매체에서는 허용되지 않습니다(선행 전기 쌍극자 ^[1]기여에서).그러나, 2단계 시스템이 그들의 전이 주파수와 비슷한 라비 주파수에서 구동될 때 발견되는 Bloch-Siegert 이동(진동)과 같은 효과는 중심대칭 시스템에서 두 번째 고조파 발생을 일으킬 것입니다.^{[2] [3]} 또한 결정학적 점군 432에 속하는 비중심대칭 결정에서는 SHG가 불가능하며 클라인만의 조건에서는 일부 예외가 ^[6]존재하지만 422 및 622 점군의 SHG가 사라져야 합니다^[5].

경우에 따라서는 광 에너지의 거의 100%를 두 번째 고조파 주파수로 변환할 수 있습니다.이러한 경우에는 일반적으로 큰 결정을 통과하는 강력한 펄스 레이저 빔과 위상 정합을 얻기 위한 세심한 정렬이 포함됩니다.다른 경우에는 2차 하모닉 이미징 현미경과 같이 빛 에너지의 극히 일부만이 2차 하모닉으로 변환되지만, 그럼에도 불구하고 이 빛은 광학 필터를 사용하여 감지할 수 있습니다.

주파수 배가라고 불리는 두 번째 고조파를 생성하는 것도 무선 통신의 한 과정입니다. 20세기 초에 개발되어 메가헤르츠 대역의 주파수와 함께 사용되어 왔습니다.주파수 곱셈의 특별한 경우입니다.

역사

두 번째 하모니 세대는 피터 프랭큰, A.E. 힐, C.W. 피터스, G에 의해 처음 시연되었습니다.1961년 ^[7]미시간 대학교 앤아버의 와인라이히.이 시연은 레이저의 발명으로 가능해졌는데, 레이저는 필요한 고강도의 일관된 빛을 만들어냈습니다.그들은 694 nm 파장의 루비 레이저를 석영 샘플에 집속했습니다.그들은 347 nm에서 빛의 생성을 나타내는 스펙트럼을 사진 용지에 기록하면서 분광기를 통해 출력된 빛을 보냈습니다.유명한 것은 Physical Review Letters ^[7]저널에 실렸을 때 복사 편집자가 사진 용지의 희미한 부분(347 nm)을 먼지의 얼룩으로 착각하여 ^[8]출판물에서 제거했다는 것입니다.SHG의 제형은 1962년 ^[9]하버드 대학의 N. Bloembergen과 P. S. Pershan에 의해 처음 기술되었습니다.선형 매질과 비선형 매질 사이의 평면 계면에서 맥스웰 방정식의 광범위한 평가에서 비선형 매질에서 빛의 상호작용에 대한 몇 가지 규칙이 설명되었습니다.

수정체의 종류

임계 위상 정합

2차 고조파 생성은 0, I 및 II로 표시되는 임계 위상 ^[10]정합을 위해 세 가지 유형으로 발생합니다.타입 0 SHG에서는 결정에 대해 특이한 편광을 가진 두 광자가 결합하여 주파수/에너지가 두 배이고 특이한 편광을 가진 단일 광자를 형성합니다.타입 I SHG에서는 결정에 대해 일반적인 편광을 갖는 두 광자가 결합하여 주파수와 특별한 편광을 갖는 하나의 광자를 형성합니다.Type II SHG에서는 직교편파를 갖는 두 개의 광자가 결합하여 주파수와 일반편파의 두 배를 갖는 하나의 광자를 형성합니다.주어진 결정 방향에 대해, 이러한 유형의 SHG만 발생합니다.일반적으로 유형 0 상호 작용을 활용하려면 준상 일치 결정 유형이 필요합니다. 예를 들어 주기적으로 폴링되는 니오베이트 리튬(PPLN)이 필요합니다.

중요하지 않은 위상 정합

위상 정합 공정은 기본적으로 광학 지수 n을 λ와 2λ로 조정하는 것을 의미하기 때문에 n이 온도에 따라 변하기 때문에 일부 복굴절 결정에서 온도 제어를 통해 수행할 수도 있습니다.예를 들어, LBO는 1200 또는 1400 ^[11]nm에서 여기된 SHG의 경우 25 °C에서 완벽한 위상 정합을 보여주지만, SHG의 경우 200 °C에서 1064 nm의 일반적인 레이저 라인으로 상승시켜야 합니다.일반적인 위상 정합처럼 결정 방향에 의존하지 않기 때문에 "비임계"라고 불립니다.

광이중하모닉

반전 대칭이 있는 매체는 (3차 고조파 생성과 달리) 선도적인 전기 쌍극자 기여를 통해 2차 고조파 빛을 생성하는 것이 금지되기 때문에 표면과 인터페이스는 SHG로 연구하기에 흥미로운 주제가 됩니다.실제로, 2차 고조파 생성 및 합 주파수 생성은 대량의 신호를 구별하여 표면 특정 기술로 암묵적으로 라벨링합니다.1982년, T. F. 하인즈와 Y. R. 셴은 SHG가 ^[12]표면에 흡착된 분자 단층을 탐사하는 분광 기술로 사용될 수 있음을 처음으로 명백하게 증명했습니다.Heinz와 Shen은 레이저 염료 로다민의 단일층을 평면상의 융합 실리카 표면에 흡착시켰고, 코팅된 표면은 나노초의 초고속 레이저에 의해 펌핑되었습니다.흡착된 분자의 특징적인 스펙트럼을 갖는 SH 광과 그 전자적 전이는 표면으로부터의 반사로 측정되었고 펌프 레이저 파워에 대한 2차 파워 의존성을 보여주었습니다.

SHG 분광기에서, 표면에 대한 정보를 드러내기 위해 들어오는 $전기장{\displaystyle }$ E${\displaystyle (\lambda )}$ ${\displaystyle$ E$(\omega)}$가 주어지면 입사 주파수 2π의 두 배를 측정하는 것에 중점을 둡니다.간단히 말하면, (아래의 좀 더 심층적인 유도를 위해) 단위 부피당 유도된 2차 조화 쌍극자 $P{\displaystyle {}^{}}$(${\displaystyle 2^{}}$) (${\displaystyle 2}$ω )$${\$displaystyle$ P$^{(2)}$ ($2\omega$는 다음과 같이 쓸 수 있습니다.

${\displaystyle E(2\omega )\propto P^{(2)}(2\omega )=\chi ^{(2)}E(\omega )E(\omega )}$

여기서${\displaystyle {}^{}}$χ (${\displaystyle {2)}^{}}$ ${\displaystyle \chi ^{(2)}}$는 비선형 민감도 텐서로 알려져 있으며 연구 인터페이스에서 재료의 특성입니다.$생성$된 E${\displaystyle }$(${\displaystyle 2}$㎛)$${\$displaystyle$E ($2\omega)}$와 $상응$하는${\displaystyle {}^{}}$㎛ (${\displaystyle {2)}^{}}${\$displaystyle \chi ^{(2)}}$는 표면/계면에서 분자의 방향, 표면의 계면 분석 화학 및 계면에서의 화학 반응에 대한 정보를 나타내는 것으로 나타났습니다.

평면 표면에서

이 분야의 초기 실험들은 ^[14]금속 표면으로부터 2차 조화 발전을 보여주었습니다.결국, SHG는 공기-물 인터페이스를 조사하는 데 사용되었으며, 가장 보편적인 ^[15]표면 중 하나에서 분자 방향과 순서에 대한 상세한 정보를 허용했습니다.χ${\displaystyle {(2)}^{}}$의$$특정 $요소 {\displaystyle$ \chi$^{(2$ :

${\displaystyle {\display{aligned}\chi _{zz}^{(2)}&=N_{s}\left\langle \cos ^{3}(\theta )\right\rangle \alpha _{zzz}^{(2)}\\chi _{xzx}^{(2)}&={\frac {1}{2}N_{s}\left\langle \cos(\theta )\sin ^{2}(\theta )\right\rangle \alpha _{zzz}^{(2)}\end{aligned}}}$

여기서_s N은 흡착질 밀도이고, θ는 분자 축 z가 표면 정규 Z와 이루는 각도이며, ${\displaystyle {\alpha }_{}^{}}$ ${\displaystyle z_{}^{}}$ ${\displaystyle z_{}^{}}$z ($)${\$displaystyle \alpha$ _${zzz}^{(2$)}}는$$ 계면에서 분자의 비선형 분극성의 지배적인 요소이며, 실험실 좌표 (x, y,^[16] z)가 주어지면 θ를 결정할 수 있습니다.간섭 SHG 방법을 사용하여 γ(2)의 이러한 요소를 결정함으로써, 첫 번째 분자 배향 측정은 페놀의 하이드록실 그룹이 공기-물 계면에서 물 속으로 아래쪽을 가리킨다는 것을 보여주었습니다(예상대로 수소 결합을 형성하는 하이드록실 그룹의 잠재력으로 인해).또한 평면 표면에서의 SHG는 계면에서 분자의 pK^a 및 회전 운동의 차이를 밝혀냈습니다.

평면이 아닌 표면에서

두 번째 조화광은 '국소적으로' 평면이지만 더 큰 스케일에서 반전 대칭(중심대칭)을 가질 수 있는 표면에서도 생성될 수 있습니다.구체적으로, 최근 이론은 작은 구형 입자(마이크로 및 나노미터 스케일)로부터의 SHG가 레일리 산란(흡수된 파동에서 방출된 ^[17]파동으로의 주파수 변화 없이 산란)의 적절한 처리에 의해 허용된다는 것을 보여주었습니다.작은 구의 표면에서, 반전 대칭이 깨져서 SHG와 다른 짝수 순서의 조화가 일어날 수 있습니다.

상대적으로 낮은 농도의 미세 입자 콜로이드 시스템의 경우, 총 SH $신호$ I ${\displaystyle 2_{}^{}}$ ω 총$${\$displaystyle$ I_${2\omega}}^{\text{$total$\}\}$는 다음과 같이 제공됩니다.

${\displaystyle I_{2\omega }^{\text{total}}\propto \sum \sum _{j=1}^{n}\left(E_{j}^{2\omega }\right)^{2}=n\left(E^{2\omega }\right)^{2}=nI_{2\omega}}$

$여기$서 ${\displaystyle {\mathrm{}}_{}^{}}$ 2 $∈$ {\$displaystyle$ E_${j}^{2\omega}}}$는 j번째 입자에 의해 생성된 SH 전기장이며,^[18] n개의 입자의 밀도입니다.각 입자에서 생성된 SH 광은 일관성이 있지만 다른 입자에서 생성된 SH 광에 일관성 없이 추가됩니다(밀도가 충분히 낮은 한).따라서 SH 빛은 구와 그 환경의 계면에서만 발생하며 입자-입자 상호작용과는 무관합니다.또한 두 번째 고조파 $전기장{\displaystyle }$ E${\displaystyle (2}$㎛)$${\$displaystyle$ E$(2\omega)}$는 입자의 반지름이 a인³ 것으로 나타났습니다.

구체 이외에도 막대와 같은 다른 작은 입자들도 SHG에 ^[19]의해 유사하게 연구되었습니다.작은 입자의 고정화된 시스템과 콜로이드 시스템을 모두 조사할 수 있습니다.두 번째 세대의 비평면 시스템을 사용하는 최근의 실험에는 살아있는 세포막을^[20] 가로지르는 수송 속도론과 복잡한 나노 ^[21]물질에서 SHG의 시연이 포함됩니다.

방사패턴

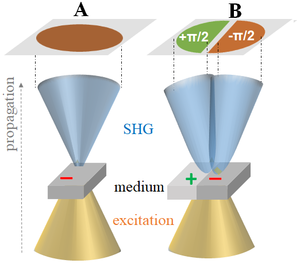
여기된 비선형 매질이 균일한 경우 여기된 가우시안 빔에 의해 생성된 SHG 방사 패턴은 또한 (균질한) 2D 가우시안 프로파일을 갖습니다.그러나 여기 빔이 빔 전파와 평행한 반대 극성(± 경계, B) 사이의 인터페이스에 위치하는 경우 SHG는 진폭이 반대 부호를 갖는 두 개의 로브로 $분할$됩니다$($즉, π${\displaystyle$ \pi$$}).

이러한 경계는 근육의 희귀체(예를 들어 = 미오신)에서 찾을 수 있습니다.여기서 우리는 오직 미래 세대만을 고려해 왔음을 주목합니다.

또한 SHG 위상 $변환$은 k → ${\displaystyle 2_{}}$ ω = - ${\displaystyle {}_{}}$ k →$$ω {\$displaystyle${\$vec {k}}_{2\omega}$=$-2{\vec {k}}_{\omega$ 일부 SHG는 역방향(epi 방향)으로도 방출됩니다.생물학적 조직에서와 같이 위상 정합이 수행되지 않을 때, 후방 신호는 충분히 높은 위상 정합에서 비롯되며,^[23] 이를 보상하기 위해 약간의 후방 기여가 가능합니다.형광과 달리 공정의 공간 간섭성은 두 방향으로만 방출하도록 제한하지만, 후방의 간섭성 길이는 항상 전방보다 훨씬 작으며, 이는 후방 SHG ^[24]신호보다 전방이 항상 더 많다는 것을 의미합니다.

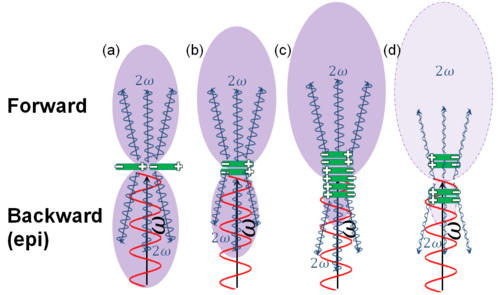
전방(F) 대 후방(B) 비율은 들뜸되는 여러 쌍극자(그림의 녹색)의 배열에 따라 달라집니다.그림의 쌍극자 (a) 하나만 가지고, F = B이지만 전파 방향 (b, c)을 따라 쌍극자를 더 쌓으면 F가 B보다 높아집니다.그러나 가우시안 빔의 Gouy 위상 이동은 초점 볼륨 가장자리에서 생성된 SHG 간에$$π {\$displaystyle$ \pi$}$ 위상 이동을 의미하며, 따라서 이 가장자리에 동일한 방향(그림의 경우(d))을 갖는 쌍극자가 있을 경우 파괴적 간섭(0 신호)이 발생할 수 있습니다.

상업용

2차 하모닉 세대는 레이저 업계에서 1064 nm 소스로 녹색 532 nm 레이저를 만드는 데 사용됩니다.1064 nm 빛은 벌크 KDP 결정을 통해 공급됩니다.고품질 다이오드 레이저에서 수정은 적외선 필터로 출력 측에 코팅되어 빔에 강렬한 1064 nm 또는 808 nm 적외선 빛이 새는 것을 방지합니다.이 두 파장 모두 눈에 보이지 않으며 눈에서 방어적인 "깜깜이 반사" 반응을 유발하지 않으므로 사람의 눈에 특별한 위험이 될 수 있습니다.또한, 아르곤 또는 다른 녹색 레이저를 위한 일부 레이저 안전 안경은 녹색 구성 요소를 걸러낼 수 있지만(잘못된 안전감을 제공) 적외선을 전송할 수 있습니다.그럼에도 불구하고 일부 "녹색 레이저 포인터" 제품은 시장에서 구입할 수 있게 되었고,^[25] 이는 종종 경고 없이 고가의 적외선 필터를 생략합니다.2차 하모닉 세대는 자기 상관기로 초단 펄스 폭을 측정하는 데도 사용됩니다.

기타 어플리케이션

초단 펄스 측정

시간 척도가 1ps(${\displaystyle {10}^{}}$- ${\displaystyle {12}^{}}$ ${\$ 10$^{-12}}$초$$) 미만이기 때문에 초단 펄스를 특성화하는 것은 전자 장치만으로 직접 할 수 없습니다. 펄스 자체를 사용해야 하므로 자동 상관 함수가 자주 사용됩니다.SHG는 두 개의 입력 필드를 혼합하여 고조파를 생성할 수 있는 장점이 있으므로, 이러한 펄스 측정을 수행하기에 좋은 후보(유일한 것은 아님)입니다.광학적 자기 상관은 현장 자기 상관과 달리 강도 또는 프린지 분해능(상호계량) 버전에서 ^[26]SHG를 사용합니다.또한, 대부분의 FROG(SHG-FROG) 버전은 지연된 ^[27]필드를 혼합하기 위해 SHG를 사용합니다.

2세대 현미경법

생물학과 의학에서, 2차 하모닉 세대의 효과는 고해상도 광학 현미경에 사용됩니다.0이 아닌 두 번째 고조파 계수 때문에, 오직 중심대칭 구조만이 SHG 빛을 방출할 수 있습니다.그러한 구조 중 하나는 대부분의 부하를 받는 조직에서 발견되는 콜라겐입니다.펨토초 레이저와 같은 단펄스 레이저와 적절한 필터 세트를 사용하면 방출된 주파수가 두 배 증가한 SHG 신호에서 여기광을 쉽게 분리할 수 있습니다.이를 통해 핀홀을 사용할 필요 없이 공초점 현미경에 버금가는 매우 높은 축방향 및 측면 해상도를 얻을 수 있습니다.SHG 현미경은 주로 콜라겐으로 구성된 각막과^[28] 라미나 크립로사 ^[29]공막의 연구에 사용되었습니다.2차 하모닉 세대는 몇몇 비 중심대칭 유기 염료에 의해 생성될 수 있지만, 대부분의 유기 염료는 2차 하모닉 세대 ^[30]신호와 함께 부수적인 형광을 발생시키기도 합니다.지금까지, 어떤 부수적인 형광을 생성하지 않고 순수하게 2차 조화 ^[30][31]세대에서 작동하는 유기 염료의 두 종류만 보여졌습니다.최근, 옥스포드 대학 연구진은 2광자 여기형 형광과 2차 고조파 기반 현미경을 이용하여 유기 포르피린형 분자가 2광자 형광과 2차 고조파 ^[32]발생에서 서로 다른 전이 쌍극자 모멘트를 가질 수 있다는 것을 보여주었습니다.그렇지 않으면 동일한 전이 쌍극자 ^[33]모멘트에서 발생하는 것으로 생각됩니다.

2차 세대 현미경은 또한 재료 과학에서 사용되는데, 예를 들어 나노 구조 ^[34]재료를 특성화하기 위해 사용됩니다.

결정성 물질의 특성화

2차 고조파 생성은 또한 비 중심대칭을 ^[36]검출하는 가장 판별적이고 신속한 기술 중 하나이기 때문에 유기 또는 무기^[35] 결정을 특성화하는 것과 관련이 있습니다.또한, 이 기술은 분말 샘플뿐만 아니라 단결정에도 사용될 수 있습니다.SHG는 비중심대칭(NC) 결정에서만 가능하다는 것을 기억해야 합니다.Nature에서 중심대칭이 아닌 결정의 비율은 중심대칭 결정보다 훨씬 낮지만(Cambridge 구조^[37] 데이터베이스의 약 22%), NC 결정의 빈도는 제약, 생물학 및 전자 분야에서 많이 증가하는데, 이는 이러한 결정의 특정한 특성(압전, 열전, polar ph) 때문입니다.asses, chirality, ...).

1968년(^[38]단결정에^[7] 대한 SHG의 첫 실험적 증거로부터 7년 후), Kurtz와 Perry는 분말 결정성 샘플에서 반전 중심의 존재 여부를 신속하게 감지하기 위한 SHG 분석기를 개발하기 시작했습니다.SHG 신호의 검출은 신뢰 수준이 99%보다 높은 결정성 비중심대칭의 검출에 대해 신뢰할 수 있고 민감한 테스트인 것으로 나타났습니다.단결정 X선 ^[39]회절에서 프리델의 법칙으로 인해 발생할 수 있는 공간군의 모호성을 해결하는 데 유용한 도구입니다.또한, 이 방법은 국제 결정학 표(International Tables for Crystalography)에 참조되어 있으며, "대칭 ^[40]중심이 없는 경우에 대해 결정성 물질을 시험하는 강력한 방법"으로 설명되어 있습니다.

제약 ^[41]산업에 특히 관심이 있는 대기업과 같은 카이랄 단계를 빠르게 구분하는 것도 한 가지 가능한 적용입니다.또한 SHG ^[43]현미경을 이용하여 100억분의 1부피까지 Kurtz&Perry 장치를 이용하여 불순물 중 하나가 검출 임계치 1ppm에^[42] 도달한 NC일 경우 재료의 구조적 순도를 조사하는 기술로 사용될 수 있습니다.

이 기술은 높은 감도로 인해 위상^[44] 다이어그램의 정확한 결정에 유용한 도구가 될 수 있으며, 적어도 하나의 위상이 ^[45][46][47]NC일 때 위상 전이(폴리모픽 전이, 탈수, ...)를 모니터링하는 데에도 사용될 수 있습니다.

이론적 유도(평면파)

낮은 전환율로

2차 조화 생성을 분석하는 가장 간단한 경우는 k 벡터 방향으로 비선형 매질을 진행하는 진폭 E(λ)의 평면파입니다.2차 고조파 ^[48]주파수에서 편광이 생성됩니다.

${\displaystyle P(2\omega )=\varepsilon _{0}\chi ^{(2)}E^{2}(\omega )=2\varepsilon _{0}d_{\text{float}}(2\omega ;\omega ,\omega )E^{2}(\omega ),\,}$

$여기$서 ${\displaystyle {\text{deff}}_{}}${\$displaystyle d_{\text{$eff$}}$는 이 특정 상호작용에 관련된${\displaystyle {}^{}}$π ($)$ {\$displaystyle \chi ^{(2)}}$의 특정 성분에 종속되는 유효 비선형 광학 계수입니다.2π에서의 파동 방정식(소규모 손실 가정 및 천천히 변하는 포락선 근사치 주장)은

${\displaystyle {\frac {\fac E(2\omega)}{\fac z}=-{\frac {i\omega}{n_{2\omega}c}}d_{\text{eff}E^{2}(\omega)e^{i\,\Delta k\,z}}$

여기서 ${\displaystyle \Delta }$ k =${\displaystyle k}$ (${\displaystyle 2}$ω ${\displaystyle )}$ - ${\displaystyle 2k}$ (${\displaystyle }$ω )$${\$displaystyle \Deltak$ =$k$ ($2\omega$) - 2$k$ (\$omega$

낮은 변환 효율(E(2π) ≪ E(ω))에서 $진폭$ E${\displaystyle (\omega )}${\$displaystyle$ E$(\omega)}$는 상호작용 길이에서 본질적으로 일정하게 유지되며, $\omega$ ${\displaystyle \ell$ $\}$입니다. 그런 다음 경계 $조건{\displaystyle }$E (${\displaystyle \mathrm{2\pi },}$ ${\displaystyle z}$ =${\displaystyle 0}$ ) = ${\displaystyle 0}${\$displaystyle$ E$(2\$omega$,z$=$$0) =$0$}을(를) 얻습니다.

${\displaystyle E(2\omega,z=\ell)=-{\frac {i\omega d_{\text{disc}}{n_{2\omega}}}{n_{2\omega}}\int_{0}^{\ell }e^{i\,\Delta k\,z}\,ω=-{\frac {i\omega d_{\text{disc}}{n_{2\omega}}}\ell \,{\frac {\sin \left\frac {1}{2}}\,\delta k\,\ell \right)}{{\frac {1}{2}},\delta k\,\ell }e^{\frac {i}{2}},\delta k\,\ell }}e^{\frac {i}{2}},\delta k\,\ell }}$

광학 강도에 $있어서$ I =${\displaystyle n}$ / ${\displaystyle 2}$ ㎛ ${\displaystyle \sqrt{0_{}}}$/ ${\displaystyle \mu 0}$ E ${\displaystyle {}^{}}${\$displaystyle$ I =$n$ / $2${\$sqrt${\$varepsilon$ _${0}/\mu$_{$0}}$ E ^{$2$ $이것$은,

${\displaystyle I(2\omega,\ell )={\frac {2\omega ^{2}d_{\text{flag}}^{2}\ell ^{2}}{n_{\omega }^{2}c^{3}\varepsilon_{0}}\left ({\frac {\sin \left ({\frac {1}{2}\,\Delta k\,\ell \right)}{\frac {1}{2}},\delta k\,\ell }\right)^{2}I^{2}(\omega )}$

이 세기는 위상 동기 조건 Δk = 0일 때 최대가 됩니다. 공정이 위상 일치하지 않으면 θ에서의 구동편광은 발생파 E(2θ)와 함께 위상에 들어가고 변환은 sin(Δkθ/2)으로 진동합니다.코히어런스 ${\displaystyle {길이}_{}}$는 π${\displaystyle {}_{}}$c = δ ℓ$$matching k ${\displaystyle \ell$ _{c$}$=${\frac {\pi$}{\Deltak$\}\}\}$로 정의됩니다. 코히어런스 길이보다 훨씬 긴 비선형 결정을 사용하는 것은 비용이 들지 않습니다. (주기적 폴링과 준위상 패턴은 이 문제에 대한 또 다른 접근법을 제공합니다.)

고갈과 함께

2차 고조파로의 변환이 중요해지면 기본값의 고갈을 포함할 필요가 있습니다.에너지 변환은 모든 관련 분야가 맨리-로우 관계를 확인한다고 명시합니다.하나는 다음과 ^[49]같은 결합 방정식을 갖습니다.

${\displaystyle {\display{aligned}{\frac {\display{aligned}{\frac E(2\omega)}{\text{eff}}{n_{2\omega}c}}d_{\text{eff}E^{2}(\omega)e^{i\,\delta k\,z},\[5pt]{\frac {i\omega}{\text{eff}}&=-{\frac {i\omega}{n_{\omega}c}d_{\text{eff}}^{*}E^{*}(\omega)e^{-i\,\delta k\,z},\end{aligned}}$

여기서 ∗ {\$displaystyle *}$는 복소수 켤레를 나타냅니다.단순화를 위해 위상 일치 생성($$ ${\displaystyle k}$ = ${\displaystyle 0}${\$displaystyle \Deltak$ =$0$})을 가정합니다.그렇다면, 에너지 절약은 다음을 요구합니다.

${\displaystyle n_{2\omega}\left[E^{*}(2\omega ){\frac {\partial E(2\omega )}{\partial z}}+{\text{c.c.}}\right]=-n_{\omega}}\left[E(\omega ){\frac {\fac {\fac E^{*}(\omega )}{\fac z}}+{\text{c.c.}}}\right]}$

${\${\$text{c.$$c$.$}}}$는 다른 항의 복소수 켤레 또는

${\displaystyle n_{2\omega}\left E(2\omega)\right ^{2}+n_{\omega} E(\omega) ^{2}=n_{2\omega}E_{0}^{2}}$

이제 우리는 다음과 같은 전제를 가지고 방정식을 풀게 됩니다.

${\displaystyle {\begin{aligned}E(\omega )&=\leftE(\omega )\righte^{i\varphi (\omega )}\E(2\omega )&=\leftE(2\omega )\righte^{i\varphi (2\omega )}\end{aligned}}$

구하다, 구하다, 구하다, 구하다, 구하다, 구하다,

${\displaystyle {\frac {d\left E(2\omega)\right }{{flag}}=-{\frac {i\omega d_{\text{flag}}{n_{\omega}c}}\left[E_{0}^{2}-\left E(2\omega )\right ^{2}\right]e^{2i\varphi (\omega )-i\varphi (2\omega )}$

로 이어집니다.

${\displaystyle \int _{0}^{\left E(2\omega)\right \ell }{\frac {d\left E(2\omega)\right }{E_{0}^{2}-\left E(2\omega)\right ^{2}}=-\int _{0}^{\ell }{\frac {i\omega d_{\text{http}}{n_{\omega}}}^{2i\varphi (\omega )-i\varphi (2\omega )}\,189.}$

사용.

${\displaystyle \int {\frac {display}{a^{2}-x^{2}}={\frac {1}{a}}\tanh ^{-1}{\frac {x}{a}}}$

우리가 얻는

${\displaystyle \left E(2\omega )\right _{z=\ell } = E_{0}\tanh \left({\frac {-iE_{0}}\ell \omega d_{\text{flag}}{n_{\omega }c}}e^{2i\varphi (\omega )-i\varphi (2\omega )}\right}.$

$실제$ ${\displaystyle {\text{deff}}_{}}${\$displaystyle d_{\text{$eff$\}\}$를 가정할 경우, 실제 고조파 성장에 대한 상대 ${\displaystyle {\mathrm{위상}}^{}}$은 e 2 i${\displaystyle {}^{}}$φ ( ω${\displaystyle {)}^{}}$ - $i$φ ( ${\displaystyle 2^{}}$ω ) = ${\displaystyle i}${\$displaystyle$ e$^{2i\varphi (\omega$) - i\$varphi (2\omega$ )} =$i$이어야 합니다.그리고나서

${\displaystyle I(2\omega,\ell )=I(\omega,0)\tanh ^{2}\left({\frac {E_{0}\omega d_{\text{time}}\ell }{n_{\omega }c}\right)}$

아니면

${\displaystyle I(2\omega,\ell )=I(\omega,0)\tanh^{2}(\Gamma \ell),}$

여기서 $\Delta$ = ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle E_{}}$0 / ${\displaystyle \mathrm{nc}}${\$displaystyle \Gamma$ =\$omega$ d_${\text{text}}$$E_{0}/nc$ I${\displaystyle }$(${\displaystyle 2}$$ω$,${\displaystyle }$$ℓ$${\displaystyle }$) +${\displaystyle I}$ (${\displaystyle }$$ω$,${\displaystyle }$$ℓ$ ) $=$${\displaystyle I}$ (${\displaystyle }$$ω$,${\displaystyle 0}$ )$${\$displaystyle$I ($2\omega,\ell$) + $I$(\$omega,\ell$ ) $=$ I$(\omega,0$부터 다음과 같습니다.

${\displaystyle I(\omega,\ell )=I(\omega,0)\operatorname {sech}^{2}(\Gamma \ell )}$

가우시안 보를 이용한 이론적 표현

여기 파형은 진폭의 가우스 빔으로 가정됩니다.$=$$A_{0}{\sqrt {\frac {2}{\pi}}}{\frac {z_{R}}{iq(z)}}\exp \left(ik_{1}{\frac {x^{2}+y^{2}}{2q(z)}\right)}$

$q{\displaystyle (z)}$ =$$z${\displaystyle }$- ${\displaystyle z}$ ${\displaystyle R_{}}$ ${\displaystyle$ q$(z$) = $z$ $-iz_{R$ z ${\displaystyle$ z$}$ 전파 방향, $z$ ${\displaystyle R_{}}$ ${\displaystyle z_{R}$ 레일리 범위, ${\displaystyle {}_{}}$ 1 ${\displaystyle {k}_{1}$ 파동 벡터.

각 파동은 파동 방정식을 검증합니다.

${\displaystyle \left[{\frac {\laude}}{\laude x^{2}}+{\frac {\laude }{\laude y^{2}}}+2ik_{1}{\frac {\laude z}}\right]A(x,y,z;k_{1})={\begin{case}0&{\text{fundament}},\{\frac {\omega_{n}^{2}c^{2}}}{\chi ^{(n)}}A(x,y,z;k_{1})e^{i\,\delta k\,z}&{\text{for }}n{\text{th-harmonic}}.\end{case}}$

여기서 ${\displaystyle \Delta }$ k = ${\displaystyle k_{}}$n - ${\displaystyle k_{}}$ 1$${\$displaystyle \Deltak$ = $k_{n}$ - $k_{1$

위상 매칭 포함

$A$ n${\displaystyle {}_{}}$= - ${\displaystyle i}$ ω n${\displaystyle }$2 n ∞ ${\displaystyle \frac{c_{}}{}}$ ( ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{02}_{}}{}}$ ω${\displaystyle \frac{}{}}$) ${\displaystyle {\sqrt{}z}^{}}$ R ${\displaystyle {}_{}^{}{}_{}^{}}$∫ - χ z ⁡ ( n ) ( u )${\displaystyle \frac{{}^{}q}{}}$(${\displaystyle \frac{{}^{}u}{}}$) ${\displaystyle \frac{2^{}}{}\frac{{}^{}}{}\mathrm{du}}$ exp${\displaystyle }$π ( i k ${\displaystyle \frac{x^{}}{}}$ 2 + y 22 ${\displaystyle \frac{q}{}}$(${\displaystyle \frac{}{}}$z${\displaystyle \frac{}{}}$)$${\$displaystyle A_{n$}=-$i{\frac${\$omega$ _${n}}{2n_{n\$omega $}c}{\left(A_{0}{\sqrt${\$frac {2}{\pi }}\right)$$^{n}}z_{R}^{2}\int _{-\infty}^{z}{\frac {\chi ^{(n)}(u)}{q(u)}}\,du\exp \left(ik_{n}{\frac {x^{2}+y^{2}}}{2q(z)}}\right)}$

(가우시안), 는 식 (SHG의 경우 n = 2)의 해입니다.

위상 일치 없음

완벽하지 않은 위상 정합은 실제로 특히 생물학적 샘플에서 더 현실적인 조건입니다.${\displaystyle {그러나}_{}}$ paraxial 근사치는 k${\displaystyle {}_{}{}_{}}$ = ${\displaystyle n_{}}$k 1 {\$displaystyle k_{$n}=nk$\_$$\{1$}}이며, 고조파 표현식에서${\displaystyle {}^{}}$χ (${\displaystyle n}$ )$$( z ) ${\displaystyle \chi$ ${\displaystyle {^\{(}^{}}$$n)}($z)}는 ${\displaystyle {\mathrm{이제}}^{}}$χ${\displaystyle {}^{}}$(${\displaystyle {}^{}}$ ) ( ${\displaystyle z^{}}$ ) ${\displaystyle e^{}}$δ k z {\$displaystyle$ \$chi ^{(n)}(z)e^{i$\,\$Delta k\,$z$\}$입니다.

SHG(n = 2)의 특수한 경우 길이 L과 초점 $위치$ z ${\displaystyle 0_{}}${\$displaystyle z_{0$의 중간에서 강도는 다음과 같이 적습니다.

${\displaystyle I_{2\omega} = {\frac {2\omega ^{2}}{\pic^{2}\varepsilon _{0}w_{0}^{2}n_{2\omega }n_{\omega }^{2}}}I_{\omega }^{2}(\chi ^{(2)}^{2}}\left(\int_{z_{0}}^{z_{0}+L}{\frac {e^{i\,\Delta k\,z}{1+iz/z_{R}}\right)^{2}\,dz.}$

$여기$서 c$${\$displaystyle$ c$}$는 진공에서의 빛의 속도이고, ε$$0 ${\displaystyle$ \$varepsilon _{$0}}은 진공 $유전율$이고, ${\displaystyle n_{}}$ω {\$displaystyle n_${n\omega$}$는 매질의 광학 지수이며, n$$ω {\$displaystyle$ n$\omega}$와 $w$ 0 ${\displaystyle w_{0}$은 여기의 허리 크기입니다.

따라서 가우시안 빔의 Gouy 위상 이동으로 인해 SHG 강도는 벌크(< < ${\displaystyle$ 0<$z_{0}< L$})에서 빠르게 감소합니다.

실험에 따라 SHG 신호는 벌크(중간 두께가 너무 크면)에서 사라지고 SHG는 재료 표면에서 생성되어야 합니다. 따라서 변환은 평면파 모델이 나타내는 것과 달리 산란자 수의 제곱으로 엄격하게 스케일링되지 않습니다.흥미롭게도, THG와 같이 더 높은 주문에 대해서도 신호가 대량으로 사라집니다.

2세대에 사용되는 재료

두 번째 고조파를 생성할 수 있는 물질은 반전 대칭이 없는 결정입니다.이를 통해 물, 입방체 대칭 결정 ^[48]및 유리가 제거됩니다.

다음은 SHG 변환을 위해 특정 유형의 레이저와 함께 사용되는 몇 가지 결정입니다.

• 600-1500 ^[51]nm에서의 기본 여기: BiBO (BiBO₃₆)
• 570-4000 ^[52]nm에서의 기본 여기: 리튬 아이오딘산염₃ LiIO.
• 800-1100, 종종 860 또는 980 ^[53]nm에서의 기본 여기: 칼륨 니오베이트 KnbO₃
• 410-2000 nm에서의 기본 여기 : BBO (β-BaBO₂₄)^[54]
• 984 nm-3400 nm에서의 기본 여기: KTP (KTiOPO₄) 또는 KTA,^[55]
• 1064 nm에서의 기본 여기 : 모노포타슘 포스페이트 KDP (KHPO₂₄), 리튬 트리보레이트 (LiBO₃₅), CsLiBO₆₁₀ 및 바륨 보레이트 BBO (β-BaBO₂₄).
• 1319 nm에서의 기본 여기 : KNbO₃, BBO (β-BaBO₂₄), 모노포타슘 포스페이트 KDP (KHPO₂₄), LiIO₃, LiNbO₃ 및 포타슘 티타닐 포스페이트 KTP (KTiOPO₄).
• ~1000~^[56]2000 nm에서의 기본 여기 : PPLN과 같은 주기적으로 폴링된 결정.

특히, 콜라겐, 튜불린 또는 미오신과 같은 원통형 대칭을 갖는 필라멘트 생물학적 단백질뿐만 아니라 특정 탄수화물(전분 또는 셀룰로스와 같은) 또한 SHG(^[57]근적외선에서 기본적인)의 상당히 좋은 변환체입니다.

참고 항목

• 반하모닉 세대
• 비선형 광학
• 광 주파수 승수기
• 이차 고조파 영상 현미경
• 자발적 매개변수 하향 변환
• 표면 2차 고조파 발생
• 고조파 발생

참고문헌

외부 링크

기사들

• Parameswaran, K. R.; Kurz, J. R.; Roussev, M. M.; Fejer (2002). "Observation of 99% pump depletion in single-pass second-harmonic generation in a periodically poled lithium niobate waveguide". Optics Letters. 27 (1): 43–45. Bibcode:2002OptL...27...43P. doi:10.1364/ol.27.000043. PMID 18007710.
• "Frequency doubling". Encyclopedia of laser physics and technology. Retrieved 2006-11-04.