방향매트로이드

지향성 항진법은 지시된 그래프의 속성, 순서된 필드에 대한 벡터 배열, 순서된 필드에 대한 하이퍼플레인 배열 등을 추상화하는 수학적 구조다.^[1]이에 비해 보통(즉, 비지향적) 매트로이드(matroid)는 반드시 지시되지 않는 그래프와 필드 위에 벡터 배열로 공통되는 의존성을 추상화하는데, 반드시 순서가 정해진 것은 아니다.^[2][3]

모든 지향성 모종에는 기저 모종이 있다.따라서 일반 매트로이드에 대한 결과는 지향적인 매트로이드에 적용될 수 있다.그러나, 그 반대는 거짓이다. 일부 매트로이드는 기초 구조(예: 회로 또는 독립형 세트)의 방향을 정하여 지향적인 매트로이드(matroid)가 될 수 없다.^[4]모성애와 지향성 모성애 사이의 구별은 아래에서 더 자세히 논의된다.

매트로이드는 종종 차원 이론과 알고리즘과 같은 분야에서 유용하다.구조물의 방향성에 대한 추가적인 세부사항 포함으로 인해, 그 유용성은 기하와 최적화를 포함한 몇 가지 영역으로 더 확장된다.

배경

세트할 그래프 가장자리의 방향 개념을 추상화하려면 세트 요소에 "방향"을 할당하는 기능이 필요하다.이것이 달성된 방법은 다음과 같은 서명된 세트의 정의에 있다.

• 서명된 $X{\displaystyle }$ ${\displaystyle X}$세트는 $X{\displaystyle {}^{}}$ ${\displaystyle \underset{}{\_}}$ ${\$ 개체 세트를 X${\displaystyle {}^{}}$+ ${\$ X$^{+}$와 X${\displaystyle {}^{}}$- ${\$ X$^{-}$의 두 하위 집합으로 결합한다$.$

$X{\displaystyle {}^{}}$+ ${\$의 멤버는 플러스 요소라고 하며, $X{\displaystyle {}^{}}$- ${\$의 멤버는 마이너스 요소다.

• $X{\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{\_}}$= ${\displaystyle {}^{}}$+ ${\displaystyle {}^{}}$ X${\displaystyle {}^{}}$- ${\$ $집합{\displaystyle }$ X$$_는 ${\displaystyle {}^{}}$ {\$displaystyle X}$의 지원이라고 한다$$$.$
• 빈 서명 세트인$,{\displaystyle \emptyset }}$은(는$)$ 빈 세트인 $\varnothing {\displaystyle \underset{}{\mathrm{}}}$ ${\displaystyle \underset{}{\_}}${\$displaystyle {\underline {\empt}}}}$과(와$$) $\varnothing {\displaystyle {\mathrm{}}^{}}$+ ${\$의 "파티션"과 결합된 빈 세트로$$ 정의된다$.$
• The signed set ${\displaystyle Y}$ is the opposite of ${\displaystyle X}$, i.e., ${\displaystyle Y=-X}$, if and only if ${\displaystyle Y^{+}=X^{-}}$ and ${\displaystyle Y^{-}=X^{+}}$

서포트 $x{\displaystyle }$ ${\displaystyle x}$의 요소를 감안하여$,$ $양$의 요소는$$ x ${\displaystyle x},$ ${\displaystyle 음}$의 요소는${\displaystyle }$- x ${\displaystyle -x}$을(를) 작성한다.이렇게 해서 서명된 집합은 구별되는 요소에 부정적인 기호를 추가하는 것일 뿐이다.이것은 우리가 더 큰 구조물의 방향을 고려할 때만 "방향"으로 의미가 있을 것이다.그러면 각 원소의 부호는 이 방향과 관련된 방향을 인코딩할 것이다.

공리화

일반 매트로이드와 마찬가지로 공리의 몇 가지 등가 시스템이 존재한다. (다중 등가 공리화를 보유한 그러한 구조를 암호형 구조라고 한다.)

회로 공리

$E{\displaystyle }$ ${\displaystyle E}$을(를) 원하는 대로 설정하십시오$$.$E{\displaystyle }$ ${\displaystyle E}$을(를) 접지 세트라고 한다.$C{\displaystyle \mathcal{}}$ ${\${$C$$}$을(를) 서명된 집합의 집합으로$$ 두십시오$.$ 각 $집합$은$$E ${\displaystyle$$${\$mathcal {C}$에 대해 다음 공리가 $C{\displaystyle \mathcal{}}$ ${\$을(를)를$($를) 유지한다면, 동일한 방향의 매트로 된 회로 집합이$$ 된다.$n{\displaystyle }$ E ${\displaystyle$ E$\}.$

• (C0) $\varnothing {\displaystyle \mathrm{}}$ ${\displaystyle \notin }$ ${\displaystyle C\mathcal{}}$ ${\${C$}}$
• (C1) (대칭) ${\displaystyle 모든\mathcal{}}$ X ${\displaystyle \in }$ C${\displaystyle }$,${\displaystyle }$- ${\displaystyle X}$ ${\displaystyle \in }$ ${\displaystyle C}$. ${\displaystyle {\text{ 모든 }}}X\in {\mathcal$ {$C},~~-\!$$X\in {\mathcal {C}.$$}$
• (C2) (incomparable) ${\displaystyle {\text{ For all }}X,Y\in {\mathcal {C}},~~{\text{ if }}{\underline {X}}\subseteq {\underline {Y}}{\text{ then }}(X=Y{\text{ or }}X=-Y).$$}$
• (C3) (weak elimination) ${\displaystyle {\text{ For all }}X,Y\in {\mathcal {C}},X\neq -Y{\text{ with an }}e\in X^{+}\cap Y^{-}{\text{ there is a }}Z\in {\mathcal {C}}{\text{ such that }}}$
  • ${\displaystyle Z^{+}\subseteq (X^{+}\컵 Y^{+}}\setminus \{e\}{\text{}}}}}}}}}}}$
  • ${\displaystyle Z^{-}\subseteq (X^{-}\cup Y^{-}}\setminus \{e\}).}$

벡터 공리음

The composition of signed sets ${\displaystyle X}$ and ${\displaystyle Y}$ is the signed set ${\displaystyle X\circ Y}$ defined by ${\displaystyle {\underline {X\circ Y}}={\underline {X}}\cup {\underline {Y}}}$, ${\display$$style (X\circ Y)^{+}=X^{+}\cup \left(Y^{+}\setminus X^{-}\right)}$, and ${\displaystyle (X\circ Y)^{-}=X^{-}\cup \left(Y^{-}\setminus X^{+}\right)}$.지향성 매트로이드의 벡터는 회로의 구성이다.지향성 매트로이드의$$ 벡터 $V{\displaystyle \mathcal{}}$ ${\$은(는) 다음 공리를 만족한다.

• ${\displaystyle \emptyset \in {\mathcal {V}}$
• ${\displaystyle {\mathcal{V}=-{\mathcal {V}}$
• 모든 $X{\displaystyle }$, ${\displaystyle Y}$ ${\displaystyle \in }$ ${\displaystyle V\mathcal{}}$ ${\$Y\$in$ {\mathcal {$V},$X${\displaystyle }$$math$ Y $cal$$$V ${\$${\displaystyle \mathrm{displaystyle}}$ $X\$circle Y\$in$ {\$mathcal {V}}$에 대해
• for all ${\displaystyle X,Y\in {\mathcal {V}}}$, ${\displaystyle e\in X^{+}\cap Y^{-}}$and ${\displaystyle f\in ({\underline {X}}\setminus {\underline {Y}})\cup ({\underline {Y}}\setminus {\underline$${X}}\cup (X^{+}\cap$ Y$^{+}}\cap$ Y$^{-}}},$ $$$Z{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle V\mathcal{}}$ ${\$cup}이(가) 있다$.$
  • ${\displaystyle {}^{}{}^{}{}^{}}$+ ${\displaystyle {}^{}}$ X${\displaystyle {}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle Y{}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle$ Z$^{+}\subset$ X$^{+}\컵$ Y$^{+}\setminus$ e$\},$
  • ${\displaystyle Z^{}}$- ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ -${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ -${\displaystyle {}^{}}$ ${\displaystyle e}$ ${\displaystyle Z^{-}\subset$ X$^{-}\컵$ Y$^{-}\setminus e}$및
  • ${\displaystyle f}$ ${\displaystyle \in }$ ${\displaystyle Z\underset{}{}}$ ${\displaystyle \underset{}{\_}}$ ${\$

치로토페 공리

$E{\displaystyle }$ ${\displaystyle E}$을(를) 위와 같이 두십시오.음이 아닌 각 정수 r ${\displaystyle r$에 대해 $순위{\displaystyle }$ r ${\displaystyle r}$의 치로토프는 다음 공리를 만족하는$$ 함수 $\chi {\displaystyle }$: ${\displaystyle E^{}}$ ${\displaystyle {}^{}}$→${\displaystyle }${${\displaystyle }$- 1,${\displaystyle 0,1}$} {\$displaystyle \chi$ \$colon$ E^{$r}\$colon $E^}\1\}이다.$

• (B0) (비경쟁): $\chi {\displaystyle }$ ${\displaystyle \chi }$이(가) 0과(와) 동일하지 않음
• (B1) (대체):For any permutation ${\displaystyle \sigma }$ and ${\displaystyle x_{1},\dots ,x_{r}\in E}$, ${\displaystyle \chi \left(x_{\sigma (1)},\dots ,x_{\sigma (r)}\right)=\operatorname {sgn} (\sigma )\chi \left(x_{1},\dot$$s ,x_{r}\right$ 여기서 ${\displaystyle \mathrm{sgn}}$ ${\displaystyle }$ (${\displaystyle \sigma }$ $){\displaystyle \operatorname {sgn} (\sigma )}$은 순열의 표시다.
• (B2) (교환):For any ${\displaystyle x_{1},\dots ,x_{r},y_{1},\dots ,y_{r}\in E}$ such that ${\displaystyle \chi (y_{i},x_{2},\dots ,x_{r})\chi (y_{1},\dots ,y_{i-1},x_{1},y_{i+1},\dots ,y_$각 $i{\displaystyle }$ ${\displaystyle i}$에 대해$$ ${r}\geq$ 0$}$을(를) 지정한 다음$,$ $\chi {\displaystyle (x{}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle }$…${\displaystyle }$,${\displaystyle y_{}}$ ${\displaystyle {}_{}}$)${\displaystyle \ge }$ $(\displaystyle \chi \left(x_{1}, x_{r}\right)\chi \left(y_{1},y_{r}\re$}\ge}\q$)\backslash$$q$}.

치로토프(chirotope)라는 용어는 화학에서 추상화된 개념인 치리성의 수학적 개념에서 유래되었는데, 여기서 반사를 제외하고 구조가 같은 분자를 구별하는 데 사용된다.

등가성

순위 $r{\displaystyle }$ ${\displaystyle r}$의 모든 치로토프는$gives{\displaystyle }$ ${\displaystyle$$r}$ -element$$ 하위 집합으로 구성된$$ $E{\displaystyle }$ ${\displaystyle$ $E$$}$에 0이 아닌 값을 할당하는$$ 매트로이드의 집합을 생성한다$$.^[5]치로토프는 매트로이드의 회로에 사인할 수 있다.If ${\displaystyle C}$ is a circuit of the described matroid, then ${\displaystyle C\subset \{x_{1},\dots ,x_{r},x_{r+1}\}}$ where ${\displaystyle \{x_{1},\dots ,x_{r}\}}$ is a basis.$그런{\displaystyle }$ 다음 C ${\displaystyle C}$을(를) 양의 요소로 서명할 수 있음$$

${\displaystyle C^{+}=\{x_{i}}:(-1)^{i}\chi(x_{1},\dots,x_{i-1},\dots,x_{r+1}=1\}}$

그리고 부정적인 요소들을 보완한다.따라서 치로토프는 지향적인 매트로이드의 지향적인 기초가 된다.이런 의미에서 (B0)은 기지의 비빈 공리, (B2)는 기본 교환 재산이다.

예

지향성 매트로이드는 지시된 그래프나 선형 불평등의 시스템에 대한 추상화로서 종종 도입된다(예: 바첼과 케른).아래는 명시적인 구성이다.

지시 그래프

digraph를 주어, 우리는 다음과 같은 방법으로 그래프의 표준회로의 서명회로를 정의한다.서명 회로 $X{\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{\_}}$ ${\$의 지원은 최소 사이클의 표준 에지 집합이다$$.$X{\displaystyle {}^{}}$ + ${\$X^{-} 방향과 일치하는 가장자리 및 X$$ ${\displaystyle {-}^{}}$${\$ $방향$과 반대되는 가장자리를 할당하는 시계 방향 또는 반시계 방향으로 순환한다$.$$f{\displaystyle \mathcal{}}$ ${\$은(는) 그러한 $모든{\displaystyle }$ X ${\$의 집합이고$,$ $C{\displaystyle \mathcal{}}$ ${\$은 지시된 그래프의 모서리 집합에 있는 지향적인 매트로이드의 서명 회로의 집합이다$$.

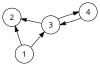
If we consider the directed graph on the right, then we can see that there are only two circuits, namely ${\displaystyle \textstyle \{(1,2),(1,3),(3,2)\}}$ and ${\displaystyle \textstyle \{(3,4),(4,3)\}}$. Then there are only four possible signed circuits correspondingto clockwise and anticlockwise orientations, namely ${\displaystyle \textstyle \{(1,2),-(1,3),-(3,2)\}}$, ${\displaystyle \textstyle \{-(1,2),(1,3),(3,2)\}}$, ${\displaystyle \textstyle \{(3,4),(4,3)\}}$, and ${\displaystyle \{-}$${\displaystyle \textstyle \{-(3,4),-(4,3)\}}$. These four sets form the set of signed circuits of an oriented matroid on the set ${\displaystyle \textstyle \{(1,2),(1,3),(3,2),(3,4),(4,3)\}}$.

선형대수학

$E{\displaystyle }$ ${\$이(가) ${\displaystyle {}^{}}$ n ${\$$^n}$의 유한 부분 집합인 경우, 최소 선형 종속 세트는 $E{\displaystyle }${\$displaystyle \textstyle E$}에 매트로이드의 회로 집합을 형성한다${\displaystyle .<img\; alt="\backslash textstyle\; E"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/baedc8b2d5a4fce1b5a81e1e60764db1c89d30c3"\; style="vertical-align:\; -0.338ex;\; width:1.776ex;\; height:2.176ex;"\; papago-attr-id="268">}$ 이 구조를 각 회로 {${\displaystyle {}_{}}{\displaystyle {1\mathrm{}}_{}}$…${\displaystyle v_{}}$ ${\displaystyle m_{}}$ ${\displaystyle {}_{}}$ ${\$ 최소한의 선형 종속성이 있음$$

${\displaystyle \sum _{i=1}^{m}\lambda _{i}v_{i}=0}$

λ 나}. 그리고 부호 있는 회로 X)({\displaystyle\textstyle X=\{X^{+},X^{-}\}}X+){vi:λ 나는입니다.;0}{\displaystyle\textstyle X^{+}=\{v_{나는}:\lambda _{나는}>, 0\}긍정적인 요소를 가지}과 부정적 요소를 R{\displaystyle\textstyle \lambda_{나는}\in \mathbb{R}∈. X−{ : < ${\$$그러한{\displaystyle }$ 모든 $X{\displaystyle }$ ${\$의 집합은 E ${\$에 있는 지향성 매트로이드의 서명 회로 집합을 형성하며$,$ 이러한 방식으로 실현될 수 있는 지향성 매트로이드를 표현 가능하다고 한다.

벡터 $E{\displaystyle }$ ${\displaystyle E}$의 동일한 집합을 고려할 때$,$ 우리는 치로토프 $\chi {\displaystyle }$: ${\displaystyle {}^{}}$ ${\displaystyle r^{}}$→${\displaystyle }${${\displaystyle }$- 1,${\displaystyle 0}$, ${\displaystyle 1}$ {\$displaystyle \chi :$$E$$$$^{r}\오른쪽$ 화살표 $\{-1,1$ 모든 x ${\displaystyle 1_{}}$에 대해${\displaystyle }$x r${\displaystyle r_{}E}$ ${\displaystyle x_{1$},\$dots$,x_${r}\in E}$

${\displaystyle \chi(x_{1},\filename ,x_{r}=\det(x_{1},\detail(x_{1},\filename,x_{r})}}$

여기서 방정식의 우측은 결정 인자의 부호다.그러면 $set{\displaystyle }$ ${\displaystyle \chi}$은(는) 세트 $E{\displaystyle }$ ${\displaystyle$ E$}$에 있는 동일한 방향 매트로이드의 치로토프 입니다$.$

하이퍼플레인 배열

실제 하이퍼플레인 배열 $A{\displaystyle \mathcal{}}$=${\displaystyle }${${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle H_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {\mathcal{A}=\{H_{1},\ldots, H_{n}\}\}}}}}}}}$는 각각 원점을 포함하는 R $d{\displaystyle {\mathbb{}}^{}}$ ${\$의 유한 집합이다$.$각 하이퍼 평면의 한 면을 양면으로 선택함으로써, 우리는 절반의 공간을 확보한다.반공간 배치는 주변 공간을 유한한 셀 집합으로 분해하며, 각 셀은 각 하이퍼플레인의 어느 쪽에 착륙하느냐에 의해 정의된다.That is, assign each point ${\displaystyle x\in \mathbb {R} ^{d}}$to the signed set ${\displaystyle X=(X^{+},X^{-})}$with ${\displaystyle i\in X^{+}}$ if ${\displaystyle x}$ is on the positive side of ${\displaystyle H_{i}}$and ${\displays$$tyle i\in X^{-}$ $만약{\displaystyle }$ x ${\$$displaystyle x}$이(가) ${\displaystyle H_{}}$ i {\displaystyle $H_{i}}$의 음측에 있다면$$$$$$.이 서명된 집합의 집합은 이중 지향성 매트로이드의 벡터인 지향성 매트로이드의 탐촉자 집합을 정의한다.^[6]

볼록 폴리토프

Günter M. Ziegler는 볼록한 폴리토페스를 통해 지향적인 매트로이드를 소개한다.

결과.

방향성

표준 매트로이드는 그 회로가 어떤 지향적인 매트로이드의 서명된 회로의 지지라면 방향성이라고 불린다.실제 대표 가능한 모든 모성애가 방향을 잡을 수 있다고 알려져 있다.또한 미성년자를 대상으로 하여 오리엔테이블 매트로이드의 등급이 폐쇄되는 것으로 알려져 있으나 오리엔테이블 매트로이드의 금지된 미성년자 명단은 무궁무진하다고 알려져 있다.^[7]이런 의미에서, 지향적인 매트로이드는 일반 매트로이드보다 훨씬 엄격한 공식화다.

이중성

모성애들은 독특한 이중성을 가지고 있고, 지향적인 모성애들은 독특한 직교 이중성을 가지고 있다.이것이 의미하는 바는 기본 매트로이드가 이중이고 모든 회로에 직교하도록 코커큐가 서명되어 있다는 것이다.두 개의 부호 집합은 지지대의 교차점이 비어 있거나 교차점에 대한 양극 요소와 교차점에 대한 음극 요소의 제한이 두 개의 비식별 및 비-반복 부호 집합을 형성하는 경우 직교한다고 한다.이중 지향성 매트로이드의 존재와 고유성은 모든 서명 회로가 서명된 모든 코코아 과자와 직교한다는 사실에 달려 있다.^[8]특수성을 위해 왜 정형성이 필요한지 알기 위해서는 위의 디그라인 예만 보면 된다.평면 그래프의 경우 회로 매트로이드의 이중은 그래프의 평면 듀얼의 회로 매트로이드라는 것을 알고 있다.따라서 그래프와 그래프의 이중 방향을 지정하는 방법만큼 이중화된 다양한 지향성 매트로이드가 있다.

이 고유한 직교 이중 지향성 매트로이드의 명시적 구조를 보려면 지향성 매트로이드의 치로토프 $\chi {\displaystyle }$: ${\displaystyle {}^{}}$ ${\displaystyle r^{}}$→${\displaystyle }${${\displaystyle }$- ${\displaystyle 1}$,${\displaystyle 0,}$ ${\displaystyle 1}$ ${\displaystyle \}}$ ${\displaystyle \chi$:$E^{r}\rightarrow \{-1,0,1\}}$. If we consider a list of elements of ${\displaystyle x_{1},\dots ,x_{k}\in E}$ as a cyclic permutation then we define ${\displaystyle \operatorname {sgn} (x_{1},\dots ,x_{k})}$ to be the sign of the associated permutation.만약${\displaystyle {}^{}}\chi {\displaystyle {}^{}}$ : ${\displaystyle E^{}}$ ${\displaystyle {}^{}}$- ${\displaystyle r^{}}$→${\displaystyle }${${\displaystyle }$- ${\displaystyle 1}$,${\displaystyle 0}$, 1 ${\displaystyle \chi ^{*}:$$E^{$E$-r}\오른쪽$ 화살표 $\{-1,1\}$은(는) 다음과 같이 정의된다.

${\displaystyle \chi ^{*}(x_{1},\dots ,x_{r})\mapsto \chi(x_{r+1},\dots ,x_{E}}}\dots ,x_{r+1},\x_{E}),}$

그러면${\$는 고유한 직교 이중 지향성 매트로이드의 치로토프다$$.^[9]

위상적 표현

모든 지향성 모형이 표현 가능한 것은 아니다. 즉, 모든 것이 점 구성 또는 동등하게 하이퍼플레인 배열로 실현되는 것은 아니다.그러나 어떤 의미에서는 모든 지향적인 모성애가 하이퍼플레인 배열이라는 실현에 가깝다.특히, 포크맨-로렌스 위상학적 표현 정리에서는 어떤 지향적인 매트로이드도 유사체의 배열로서 실현을 가지고 있다고 기술하고 있다.$d{\displaystyle }$ $[\displaystyle d}$ -차원$$ 유사권은 $e{\displaystyle }$: ${\displaystyle {}^{}}$ ${\displaystyle d^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {\mathrm{d}}^{}}$+ 1 ${\$$S^{d}\hookrightarrow S^{d+1}}$ such that there exists a homeomorphism ${\displaystyle h:S^{d+1}\rightarrow S^{d+1}}$ so that ${\displaystyle h\circ e}$ embeds ${\displaystyle S^{d}}$ as an equator of ${\displaystyle S^{d+1}}$.이런 의미에서 유사권은 (야생구와 반대되는) 길들인 구에 불과하다.$S{\displaystyle {}^{}}$ ${\displaystyle d^{}}$ ${\$의 유사권 배열은 유사점을 따라 교차하는 유사권의 집합이다.마지막으로 포크맨 로렌스 위상학적 표현 정리에서는 등급 $1의$모든 지향적 $매트리노드$를 $S{\displaystyle {}^{}}$ ${\displaystyle d^{}}$ ${\$ S$^{d}}$의 유사권 배열에서 얻을 수 있다고$$ 명시하고 있으며$,$^[10] 1978년에 출판한 존 포크맨과 짐 로렌스의 이름을 따서 명명되었다.

기하학

지향성 매트로이드 이론은 결합 기하학, 특히 볼록 폴리토페스, 조노토페스 이론과 벡터 구성(과대 평면의 범위)의 개발에 영향을 미쳤다.^[11]캐러테오도리의 정리, 헬리의 정리, 라돈의 정리, 한-바나흐의 정리, 크레인-밀만 정리, 파르카스의 보조정리 등 많은 결과들이 적절한 지향의 매트로이드를 사용하여 공식화될 수 있다.^[12]

최적화

R에 의해 지향성 매트로이드에 대한 공리계통의 개발이 시작되었다. Tyrrell Rockafellar는 단치히의 심플렉스 알고리즘의 선회작전을 통해 발생하는 행렬의 기호 패턴을 묘사했다; Rockafellar는 Albert W로부터 영감을 받았다. 터커는 "터커 테이블로"에 나오는 그런 간판 패턴에 대한 연구를 했다.^[13]

지향성 매트로이드 이론은 결합 최적화에 획기적인 발전을 가져왔다.선형 프로그래밍에서, 그것은 Robert G. Bland가 그의 선회 규칙을 공식화한 언어였고, 단순 알고리즘이 사이클을 피했다.마찬가지로, 그것은 Terlaki와 Zhang에 의해 선형 프로그래밍 문제에 대한 그들의 크라이스 크로스 알고리즘이 유한 종료를 가지고 있다는 것을 증명하기 위해 사용되었다.Todd와 Terlaki의 볼록한 2차 프로그래밍에서도 비슷한 결과가 나왔다.^[14]선형 굴절 프로그래밍,^[15] 2차 프로그래밍 문제, 선형 보완성 문제에 적용했다.^[16][17][18]

조합 최적화의 외부에서는 OM 이론이 Rockafellar의 "단방성 프로그래밍" 이론과 "증가된 하강"^[19]이라는 관련 개념에서 볼록 최소화에 나타나기도 한다.이와 비슷하게, 모계종 이론은 결합 알고리즘, 특히 탐욕스러운 알고리즘의 개발에 영향을 주었다.^[20]보다 일반적으로 탐욕스러운 것은 알고리즘의 유한 종료를 연구하는 데 유용하다.

참조

추가 읽기

책들

• Bachem, Achim; Kern, Walter (1992). Linear Programming Duality: An Introduction to Oriented Matroids. Universitext. Springer-Verlag. doi:10.1007/978-3-642-58152-6. ISBN 978-3-540-55417-2. MR 1230380.
• Björner, Anders; Las Vergnas, Michel; Sturmfels, Bernd; White, Neil; Ziegler, Günter (1999). Oriented Matroids. Encyclopedia of Mathematics and Its Applications. Vol. 46 (2nd ed.). Cambridge University Press. ISBN 978-0-521-77750-6. Zbl 0944.52006.
• Bokowski, Jürgen (2006). Computational oriented matroids. Equivalence classes of matrices within a natural framework. Cambridge University Press. ISBN 978-0-521-84930-2. Zbl 1120.52011.
• Lawler, Eugene (2001). Combinatorial Optimization: Networks and Matroids. Dover. ISBN 978-0-486-41453-9. Zbl 1058.90057.
• Evar D. Nering과 Albert W. 1993년, Tucker, Linear Programs and Related Programs, Academic Press.(iii)
• Rockafellar, R. Tyrrell (1984). Network Flows and Monotropic Optimization. Wiley-Interscience. 1998년 디미트리 베르체카스의 아테나 사이언티픽에 의해 다시 출판되었다.
• Ziegler, Günter M. (1994). Lectures on Polytopes. New York: Springer-Verlag.
• Richter-Gebert, Jürgen; Ziegler, Günter M. (1997). "Oriented Matroids". In Goodman, Jacob E.; O'Rourke, Joseph (eds.). Handbook of Discrete and Computational Geometry. Boca Raton: CRC Press. pp. 111–132. ISBN 9780849385247.

기사들

• A. 바첼, A.Wanka, 지향적인 모성애에 대한 분리 이론, 이산 수학. 70 (1988) 303—310.
• 로버트 G. 블랑드, 심플렉스 방법인 수학의 새로운 유한 선회 규칙. 작전. 103–107. 103–107.
• Folkman, Jon; Lawrence, Jim (October 1978). "Oriented Matroids". J. Combin. Theory Ser. B. 25 (2): 199–236. doi:10.1016/0095-8956(78)90039-4.
• Fukuda, Komei; Terlaky, Tamás (1997). Thomas M. Liebling; Dominique de Werra (eds.). "Criss-cross methods: A fresh view on pivot algorithms" (PDF). Mathematical Programming, Series B. Amsterdam: North-Holland Publishing Co. 79 (1–3): 369–395. doi:10.1007/BF02614325. MR 1464775. S2CID 2794181.
• Fukuda, Komei; Namiki, Makoto (March 1994). "On extremal behaviors of Murty's least index method". Mathematical Programming. 64 (1): 365–370. doi:10.1007/BF01582581. MR 1286455. S2CID 21476636.
• Illés, Tibor; Szirmai, Ákos; Terlaky, Tamás (1999). "The finite criss-cross method for hyperbolic programming". European Journal of Operational Research. 114 (1): 198–214. CiteSeerX 10.1.1.36.7090. doi:10.1016/S0377-2217(98)00049-6. ISSN 0377-2217.
• R. Tyrrell Rockafellar.조합 수학 및 응용 프로그램, R. C. Bose 및 T. A. Dowling(eds), 노스캐롤라이나 출판사의 유니브, 1969년, 104-127년$,$ R ${\displaystyle n^{}}$ ${\$ R$^{n}}$의 하위 공간의 기본 벡터.
• Roos, C. (1990). "An exponential example for Terlaky's pivoting rule for the criss-cross simplex method". Mathematical Programming. Series A. 46 (1): 79–84. doi:10.1007/BF01585729. MR 1045573. S2CID 33463483.
• Terlaky, T. (1985). "A convergent criss-cross method". Optimization: A Journal of Mathematical Programming and Operations Research. 16 (5): 683–690. doi:10.1080/02331938508843067. ISSN 0233-1934. MR 0798939.
• Terlaky, Tamás (1987). "A finite crisscross method for oriented matroids". Journal of Combinatorial Theory. Series B. 42 (3): 319–327. doi:10.1016/0095-8956(87)90049-9. ISSN 0095-8956. MR 0888684.
• Terlaky, Tamás; Zhang, Shu Zhong (1993). "Pivot rules for linear programming: A Survey on recent theoretical developments". Annals of Operations Research. 46–47 (1): 203–233. CiteSeerX 10.1.1.36.7658. doi:10.1007/BF02096264. ISSN 0254-5330. MR 1260019. S2CID 6058077.
• 마이클 J.Todd, 선형 및 2차 프로그래밍(향상된 모종, J. Combin). 이론 서. B 39 (1985) 105—133.
• Wang, Zhe Min (1987). "A finite conformal-elimination free algorithm over oriented matroid programming". Chinese Annals of Mathematics (Shuxue Niankan B Ji). Series B. 8 (1): 120–125. ISSN 0252-9599. MR 0886756.

웹에서

• Ziegler, Günter (1998). "Oriented Matroids Today". The Electronic Journal of Combinatorics: DS4: Sep 10–1998. doi:10.37236/25.
• Malkevitch, Joseph. "Oriented Matroids: The Power of Unification". Feature Column. American Mathematical Society. Retrieved 2009-09-14.

외부 링크

• 후쿠다 고메이(ETH Zentrum, 취리히)와 함께 Oriented Matroid 프로그래밍을 포함한 출판물(1982년 박사 논문)
• 출판물이 있는 타마스 텔라키(레하이 대학)