파푸스 육각 정리
Pappus's hexagon theorem
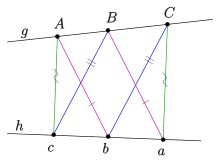
수학에서 파푸스의 육각 정리(알렉산드리아의 파푸스에게 귀속됨)는 다음과 같이 말합니다.
- given one set of collinear points and another set of collinear points then the intersection points of line pairs and and 과 는 파퍼스 선 위에 놓이면서 공선입니다. 이 세 점은 육각형 의 "반대" 면의 교차점입니다
모든 필드에 대한 투영 평면에서 유지되지만 비가환 분할 링에 대한 투영 평면에서는 실패합니다.[1] "정리"가 유효한 사영 평면을 파피안 평면이라고 합니다.
파퍼스 선 가 무한대의 선이 되도록 사영 평면을 제한하면 두 번째 다이어그램에 표시된 파퍼스 정리의 아핀 버전을 얻을 수 있습니다.
파퍼스 선 와 g g가 공통점을 가지면 이른바 작은 버전의 파퍼스 정리를 얻게 됩니다.[2]
이 입사 정리의 이중은 한 동시 선 A B A, 와 다른 동시 선 a b a, c가 주어지면 선 x, defined by pairs of points resulting from pairs of intersections and and and are concurrent. (Concurrent means that the lines pass through one point.)
파푸스의 정리는 원뿔에 대한 파스칼의 정리의 특별한 경우로, 원뿔이 2개의 직선으로 퇴화할 때의 한계 경우입니다. 파스칼의 정리는 차례로 케일리-바흐라흐 정리의 특별한 경우입니다.
파퍼스 구성은 파퍼스 정리에서 발생하는 9개의 선과 9개의 점으로 구성된 것으로 각 선은 점의 3개를 만나고 각 점은 3개의 선을 만나는 것입니다. 일반적으로 파퍼스 선은 와 의 교차점을 통과하지 않습니다[3] 이 구성은 셀프 듀얼입니다. 특히, 선 는 이중 정리의 x x,의 속성을 가지며, Z의 공선성은 의 동시성과 동일하므로 그러므로 이중 정리는 그 정리 자체와 똑같습니다. 파푸스 구성의 Levi 그래프는 18개의 꼭짓점과 27개의 모서리를 가진 이분법적 거리 규칙 그래프인 파푸스 그래프입니다.
증명 : 아핀폼

만약 진술의 아핀 형태가 증명될 수 있다면, 파퍼스 정리의 사영 형태가 증명되는데, 파퍼스 평면의 사영 평면으로의 확장은 독특하기 때문입니다.
아핀 평면에서의 평행성 때문에 ∦ h g\n 두 경우를 구별해야 합니다.\} 및 g h g\ h}입니다. 간단한 증명의 핵심은 "적절한" 좌표계를 도입할 수 있는 가능성입니다.
사례 1: g 는 S = ∩ h {\displaystyle S = g\cap}에서 교차합니다.
경우 S = A = (0, 1 ), c = (1, 0 ) {\displaystyle \;S = (0, 0),\;A = (0, 1),\;c = (1, 0)\;}와 같은 좌표가 도입됩니다(도형 참조). 의 좌표는 C = , δ ∉ {0, 1} {\displaystyle ;B = (0,\gamma),;C = (0,\)amma \n입니다.
선 C 의 평행도에서 =(δ γ, {\displaystyle b = ({\tfrac {\delta }{\gamma }, 0)}을 얻고 선 A b, B {\displaystyle Ab, Ba}의 평행도에서 a = (δ, 0) {\displaystyle a = (\delta, 0)을 얻을 수 있습니다. 따라서 선 의 기울기는 이며 평행선 입니다
사례 2: ∥ h h\} (작은 정리).
이 경우 좌표는 = b = (1, 0), A = (0, 1), B = (γ, 1), γ ≠ 0 {\displaystyle \;c = (0, 0),\;b = (1, 0),\;A = (0, 1),\;B = (\gamma,),\;\n gamma \n와 같이 선택됩니다. 0 From the parallelity of and one gets and , respectively, 적어도 병렬 ∥ Ca Ca\;}.
동차 좌표를 사용한 증명
동차 좌표를 선택합니다.
- .
A 선에서 x = x x = x x 2 = x 1 {\ x_{2} = x_{3},\;x_{1} = x_{3},\;x_{2} = x_{1}}} 선에서 점 B, Y, b {\displaystyle B,Y,b}를 선택합니다.
r 세 개의 선 {\는 = p x = 3 x 3 = x 1 r {\displaystyle x_{1} = x_{2}p,\;x_{2} = x_{3}q,\;x_{3} = x_{1}r}입니다. r p = {\display rqp = 1}인 경우에만{\ a 가 점을 통과합니다. 식 = x = 3 x 3 = x 2 r {\displaystyle x_{2} = x_{1} q,\;x_{1} = x_{3}의 세 선 b, 및 X XY에 대한 조건, to pass through the same point is . So this last set of three lines is concurrent if all the other eight sets are because multiplication is commutative, so . Equivalently, are collinear.
위의 증명은 또한 파푸스의 정리가 나눗셈 링 위의 사영 공간에 대해 성립하려면 나눗셈 링이 (가환)장이라는 것이 충분하고 필요하다는 것을 보여줍니다. 독일 수학자 게르하르트 헤센베르크는 파푸스의 정리가 데사르게스의 정리를 의미한다는 것을 증명했습니다.[4][5] 일반적으로 파푸스의 정리는 어떤 사영 평면이 교환장 위의 사영 평면인 경우에만 성립합니다. 파푸스의 정리가 성립하지 않는 사영 평면은 비가환 나눗셈 고리 위의 데사르게우스 사영 평면과 비 데사르게우스 평면입니다.
이(가) 공선인 경우 이 증명은 유효하지 않습니다. 이 경우, 예를 들어 다른 투영 참조를 사용하여 대안적인 증명을 제공할 수 있습니다.
이중정리
사영 평면에 대한 이중성의 원리 때문에 파푸스의 이중 정리는 참입니다.
c{\ b,a, B, {\displaystyle A, b, C, a, c 선을 이G, {\ G인 두 연필에서 번갈아 선택하면 선이 표시됩니다
는 동시에 발생합니다. 즉, 으로 점 U {\ U이(가 .
왼쪽 다이어그램은 투영 버전(오른쪽은 아핀 버전)을 보여주며, 점 H 는 무한대의 점입니다. 점 U가 선 위에 있으면 파퍼스 정리의 "듀얼 리틀 정리"를 얻을 수 있습니다.
- 이중 정리: 사영 형식
- 이중 정리: 아핀 형태
만약 이중 "작은 정리" 점 {\ U의 아핀 버전에서도 무한대의 점이 있다면, 삼각형의 변에 있는 6개의 점에 대한 진술인 톰센의 정리를 얻을 수 있습니다(그림 참조). 톰센 도형은 공리적으로 정의된 사영 평면을 조정하는 중요한 역할을 합니다.[6] 톰센 도형의 폐쇄에 대한 증명은 위에서 제시한 "작은 정리"에 대한 증명으로 덮여 있습니다. 하지만 간단한 직접적인 증거도 있습니다.
톰센 정리의 문장(그림의 종결)은 연결, 교차 및 평행이라는 용어만을 사용하기 때문에 문장은 유한 불변이며 P =( Q = (1, 0), R = (0, 1) {\displaystyle P = (0, 0),\;Q = (1, 0),\;R = (0, 1)}와 같은 좌표를 도입할 수 있습니다(오른쪽 다이어그램 참조). 화음 순서의 시작점은(λ)입니다. lambda)} 다이어그램에서 주어진 점들의 좌표를 쉽게 확인할 수 있는데, 이는 마지막 점이 첫 번째 점과 일치한다는 것을 보여줍니다.
- 파퍼스의 작은 정리의 이중 정리로서 ( 도 무한대입니다!), 탐슨 도형(삼각형 의 점 6 2, 3, 4, 5
- 톰센 도형: 증명
정리의 다른 문장

파푸스 정리와 그 이중성에 대한 위의 특징 외에도 다음과 같은 문장들이 있습니다.
- 육각형의 6개의 꼭짓점이 두 선 위에 교대로 놓이면, 서로 반대되는 변 쌍의 교점 세 점은 공선입니다.[7]
- (위의 그림과 설명처럼) 9개의 점으로 이루어진 행렬로 배열되고 영구적인 것을 평가하는 것으로 생각됩니다. 처음 두 행과 여섯 개의 "대각형" 삼각형이 일직선이 되면 세 번째 행은 일직선이 됩니다.
- 즉, Z, X Y, B \ 가 선일 경우, 파퍼스 정리에 따르면 는 선이어야 합니다. 또한( B, C 등이 동시선의 세 배일 때 정리의 이중 형식에도 동일한 행렬 공식이 적용됩니다.[8]
- 두 개의 서로 다른 선 각각에 세 개의 서로 다른 점이 주어지면 두 선 중 하나의 점과 다른 선의 점이 쌍을 이루면 쌍을 이루지 않는 점의 결합은 선을 따라 있는 점에서 (반대로) 쌍을 이루게 됩니다.[9]
- 두 개의 삼각형이 적어도 두 가지 다른 방식으로 원근법이라면, 그들은 세 가지 방식으로 원근법입니다.[4]
- If and are concurrent and and are concurrent, then and are concurrent.[8]
오리진스
파푸스의 정리는 파푸스 모음집 7권의 명제 138, 139, 141, 143입니다.[10] 유클리드의 포리스즘 세 권 중 첫 번째 책까지 레마로 구성된 제7권의 부분에 나오는 레마 12, 제13, 제15, 제17권이 그것입니다.
레마는 오늘날 4개의 공선점의 교차비로 알려진 측면에서 증명됩니다. 이전 세 개의 레몬이 사용되었습니다. 이들 중 첫 번째인 렘마 III는 아래 그림을 가지고 있습니다(파푸스의 글자를 사용하여 γ은 G, δ은 D, θ은 J, λ은 L입니다).
여기서 AB, AG 및 AD의 동시 직선 3개는 J에서 동시에 나타나는 JB 및 JE의 두 선으로 교차됩니다. 또한 KL은 AZ와 평행하게 그려집니다. 그리고나서
- KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB).
이러한 비율은 오늘날 방정식으로 기록될 수 있습니다.[11]
- KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB).
오늘날 공선점 J, G, D, B의 교차비는 (J, G, D, B)로 표시되며, 이 순서에 따라 J, G, D, B의 마지막 화합비(즉, JD: G & B)로 표시됩니다. 따라서 우리는 이것이 A에서 동시에 나타나는 세 직선을 가로지르는 특정 직선 JD의 선택과는 무관하다는 것을 보여주었습니다. 특히
- (J, G; D, B) = (J, Z; H, E).
직선 JE가 A의 어느 쪽에 떨어지든 상관없습니다. 특히 다음 그림, 즉 보조정리 X에 대한 그림과 같은 상황이 발생할 수 있습니다.
이전과 마찬가지로 (J, G; D, B) = (J, Z; H, E)가 있습니다. 파퍼스는 이를 명시적으로 증명하지는 않지만, 보조 X는 그 반대입니다. 즉, 이 두 교차비가 같고 직선 BE와 DH가 A에서 교차하면 점 G, A, Z가 일직선이 되어야 한다는 것입니다.
우리가 원래 보여준 것은 (J, ∞; K, L) = (J, G; D, B)로 적을 수 있으며, ∞는 JK와 AG의 (none 존재) 교차점을 대신합니다. 파푸스는 실제로 렘마 XI에서 이를 보여주지만, 그 도표는 다른 문자를 가지고 있습니다.
파퍼스가 보여주는 건 DE.ZH : EZ.HD :: GB : BE, 우리가 다음과 같이 쓸 수 있습니다.
- (D, Z; E, H) = (∞, B; E, G).
보조정리 X에 대한 도표II는.
보조정리 X에 대한 도표III는 동일하지만 BA와 DG는 N에서 만납니다. 어쨌든, G를 통과하는 직선들은 A를 통과하는 세 직선들에 의해 절단되고 (그리고 교차비의 방정식들은 원소들의 순열 후에도 유효하다는 것을 받아들임) 우리는 보조정리 III 또는 XI에 의해
- (G, J; E, H) = (G, D; ∞ Z).
D를 통과하는 직선을 B를 통과하는 세 직선으로 절단한 것을 고려하면, 우리는
- (L, D; E, K) = (G, D; ∞ Z).
따라서 (E, H; J, G) = (E, K; D, L), 따라서 보조정리 X에 의해 점 H, M, K는 일직선이 됩니다. 즉, 육각형 ADEGBZ의 양변 쌍의 교점은 일직선입니다.
Lemas XV와 XVII는 점 M이 HK와 BG의 교점으로 결정되면 점 A, M, D가 일직선을 이룬다는 것입니다. 즉, 육각형 BEKHZG의 양변 쌍의 교점은 일직선입니다.
메모들
- ^ 콕서터, 236-7쪽
- ^ 롤프 링겐베르크: 그룬들라겐 데어 지오메트리, BI-Taschenbuch, 1969, 페이지 93
- ^ 그러나 이는 {\와 {\가 원근법으로 볼 때 발생합니다. 즉, {\와 가 동시에 발생합니다.
- ^ a b 콕서터 1969, 238쪽
- ^ Hessenberg(1905)의 최초 증명은 완전하지 않으며, 그는 Desargues 구성에서 몇 가지 추가적인 사건이 발생할 수 있다는 가능성을 무시했습니다(Dembowski 1968, pg. 159, 각주 1). 완전한 증거는 1953년 Cronheim에 의해 제공됩니다.
- ^ W. Blaschke: 프로젝티브 지오메트리, 스프링어-베를라그, 2013, ISBN3034869320, S. 190
- ^ 콕서터, 231쪽
- ^ a b 콕서터, 233쪽
- ^ Whicher, 14장
- ^ 히스(Vol. II, 페이지 421)는 이러한 명제를 인용합니다. 후자의 두 가지는 전자의 두 가지 대화로 이해할 수 있습니다. 클라인(128쪽)은 명제 139만을 인용하고 있습니다. 명제의 번호는 Hultsch가 할당한 것과 같습니다.
- ^ 위의 표기법을 사용하는 이유는 고대 그리스인들에게 비율은 숫자나 기하학적 대상이 아니기 때문입니다. 오늘날 우리는 비율을 기하학적 대상 쌍의 등가 클래스로 생각할 수 있습니다. 또한 그리스인들에 대한 평등은 오늘날 우리가 합동이라고 부를 수 있는 것입니다. 특히, 별개의 선분은 동일할 수 있습니다. 이러한 의미에서 비율은 동일하지 않지만 동일할 수 있습니다.
참고문헌
- Coxeter, Harold Scott MacDonald (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50458-0, MR 0123930
- Cronheim, A. (1953), "A proof of Hessenberg's theorem", Proceedings of the American Mathematical Society, 4 (2): 219–221, doi:10.2307/2031794, JSTOR 2031794
- Dembowski, Peter (1968), Finite Geometries, Berlin: Springer-Verlag
- Heath, Thomas (1981) [1921], A History of Greek Mathematics, New York: Dover Publications
- Hessenberg, Gerhard (1905), "Beweis des Desarguesschen Satzes aus dem Pascalschen", Mathematische Annalen, Berlin / Heidelberg: Springer, 61 (2): 161–172, doi:10.1007/BF01457558, ISSN 1432-1807, S2CID 120456855
- Hultsch, Fridericus (1877), Pappi Alexandrini Collectionis Quae Supersunt, Berlin
{{citation}}: CS1 maint: 위치 누락 게시자(링크) - Kline, Morris (1972), Mathematical Thought From Ancient to Modern Times, New York: Oxford University Press
- Pambuccian, Victor; Schacht, Celia (2019), "The axiomatic destiny of the theorems of Pappus and Desargues", in Dani, S. G.; Papadopoulos, A. (eds.), Geometry in history, Springer, pp. 355–399, ISBN 978-3-030-13611-6
- Whicher, Olive (1971), Projective Geometry, Rudolph Steiner Press, ISBN 0-85440-245-4
외부 링크
- 절단 매듭에서 파푸스의 육각 정리
- 절단 매듭에서 파푸스의 육각 정리에 대한 이중
- 파푸스의 정리: 9개의 증명과 3개의 변량







 파퍼스 선 위에 놓이면서
파퍼스 선 위에 놓이면서 
 무한대의 선이 되도록 사영 평면을 제한하면 두 번째 다이어그램에 표시된 파퍼스 정리의 아핀 버전을 얻을 수 있습니다.
무한대의 선이 되도록 사영 평면을 제한하면 두 번째 다이어그램에 표시된 파퍼스 정리의 아핀 버전을 얻을 수 있습니다.  공통점을 가지면 이른바 작은 버전의 파퍼스 정리를 얻게 됩니다.
공통점을 가지면 이른바 작은 버전의 파퍼스 정리를 얻게 됩니다.










 기울기는
기울기는 평행선
평행선 






















 점
점 



 원근법이며
원근법이며

 선일 경우, 파퍼스 정리에 따르면
선일 경우, 파퍼스 정리에 따르면 
 동시선의 세 배일 때 정리의 이중 형식에도 동일한 행렬 공식이 적용됩니다.
동시선의 세 배일 때 정리의 이중 형식에도 동일한 행렬 공식이 적용됩니다.







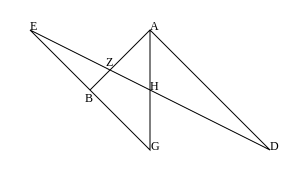


 동시에 발생합니다.
동시에 발생합니다.

