로젠브록 함수

수학적 최적화에서 로젠브록 함수는 하워드 H. 로젠브록스가 1960년에 도입한 비컨벡스 함수로 최적화 알고리즘의 성능시험 문제로 사용된다.^[1]로젠브록의 계곡이나 로젠브록의 바나나 기능으로도 알려져 있다.

전지구적 최소치는 길고 좁고 포물선 모양의 평평한 계곡 안에 있다.계곡을 찾는 것은 하찮은 일이다.그러나 세계 최소치로 수렴하는 것은 어렵다.

함수는 다음과 같이 정의된다.

${\displaystyle f(x,y)=(a-x)^{2}+b(y-x^{2})^{2}}$

$({\displaystyle x}$, ${\displaystyle y}$)${\displaystyle }$= ( , ${\displaystyle {2\mathrm{}}^{}}$)${\displaystyle (x,y)=($${\displaystyle a}$$,a^{$2$\})$에서 $글로벌$ 최소값을 가지며, 여기서 $f{\displaystyle }$ ( x${\displaystyle }$,${\displaystyle y}$) = ${\displaystyle 0}${\$displaystyle f(x,y)=0$ 일반적으로 이러한 파라미터는 $a{\displaystyle }$= ${\displaystyle 1}$ ${\$$displaystystyle$ a$=$$1$},$b$$=$과 같이 설정된다$.$$a{\displaystyle }$= ${\displaystyle 0}$ ${\displaystyle a=0}$이(가) 있는 사소한 경우에만 함수는$$ 대칭이고 최소값은 원점에 있다.

다차원 일반화

일반적으로 두 가지 변형이 있다.

하나는 $N{\displaystyle }$/ ${\displaystyle 2\mathrm{}}$ ${\displaystyle N/2}$의 결합되지$$ 않은 2D Rosenbrock 문제의 합이며, 다음 $N{\displaystyle }${\$displaystyle$N}$s$에 대해서만 정의된다.

${\displaystyle f(\mathbf {x} )=f(x_{1},x_{2},\dots ,x_{N})=\sum _{i=1}^{N/2}\left[100(x_{2i-1}^{2}-x_{2i})^{2}+(x_{2i-1}-1)^{2}\right].}$^[3]

이 변종에는 예측 가능한 간단한 해결책이 있다.

두 번째, 좀 더 관련이 있는 변종은

${\displaystyle f(\mathbf {x} )=\sum _{i=1}^{N-1}[100(x_{i+1}-x_{i}^{2})^{2}+(1-x_{i})^{2}]\quad {\mbox{where}}\quad \mathbf {x} =(x_{1},\ldots ,x_{N})\in \mathbb {R} ^{N}.}$^[4]

has exactly one minimum for ${\displaystyle N=3}$ (at ${\displaystyle (1,1,1)}$) and exactly two minima for ${\displaystyle 4\leq N\leq 7}$—the global minimum of all ones and a local minimum near ${\displaystyle {\hat {\mathbf {x} }}=(-1,1,\dots ,1)}$. This resUlt는 함수 구배를 0으로 설정하여 얻는다. 결과 $방정식$이 x$${\$displaystyle$ x$}$의 합리적인 함수임을 알아차린다$.$ $작은{\displaystyle }$ N ${\displaystyle N}$의 경우 다항식을$$ 정확하게 결정할 수 있고 Sturm의 정리를 사용하여 실제 뿌리의 수를 결정할 수 있다. 반면에 뿌리는 t로 경계할 수 있다. < ${\displaystyle x_{i} <2.$4^[5] . 더 큰 $N{\displaystyle }$ ${\displaystyle N}$의 경우 이 방법은$$ 관련된 계수의 크기 때문에 분해된다.

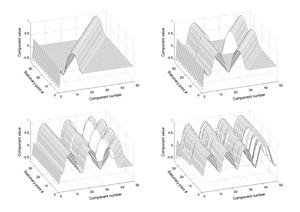
정지점

함수의 고정점 중 많은 부분이 플롯되었을 때 규칙적인 패턴을 보인다.^[5]이 구조물은 그들을 찾기 위해 이용될 수 있다.

최적화 예제

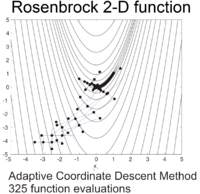
로젠브록 기능은 구배 정보를 사용하지 않고 국소 근사 모델을 구축하지 않고도 적절한 좌표계를 조정하여 효율적으로 최적화할 수 있다(많은 파생되지 않은 최적화자와 대조적으로).다음 그림은 시작점 ${\displaystyle {x\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$=${\displaystyle }$(${\displaystyle }$- 3${\displaystyle }$,${\displaystyle }$- ${\displaystyle 4}$) ${\displaystyle x_{0}=(-3,-4)}$에서 적응형 좌표 강하를 통한 2차원 로젠브록 함수 최적화의 예를 보여준다$.$함수 값 ${\displaystyle {10}^{}}$- ${\displaystyle {10}^{}}$ ${\$을 가진 용액은 325 함수 평가 후에 찾을 수 있다$$.

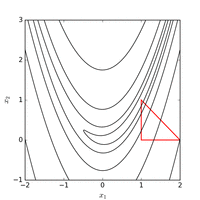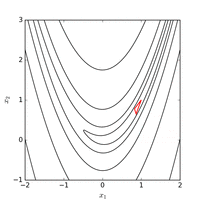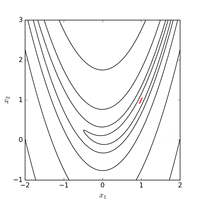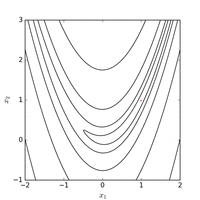
시작점 $x{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$=${\displaystyle }$(${\displaystyle }$- ${\displaystyle 1}$,${\displaystyle 1}$)${\displaystyle x_{0}=(-1,1)}$에서 Nelder-Mead 방법을 사용하여 185 기능 평가 후$$ $함수$ 값 1${\displaystyle .36}$⋅ ${\displaystyle {10}^{}}$- ${\displaystyle {10}^{}}$ ${\$로 최소값을 구한다.아래의 그림은 알고리즘의 진화를 시각화한다.

참고 항목

• 최적화를 위한 테스트 함수

참조

외부 링크

• 로젠브록 함수 3D
• Weisstein, Eric W. "Rosenbrock Function". MathWorld.