최적화를 위한 테스트 함수
Test functions for optimization응용수학에서 인공경관이라고 알려진 시험함수는 다음과 같은 최적화 알고리즘의 특성을 평가하는 데 유용하다.
- 수렴율.
- 정밀도
- 강건함.
- 일반 공연.
여기서 몇 가지 시험 기능은 최적화 알고리즘이 이러한 종류의 문제에 대처할 때 직면해야 하는 다양한 상황에 대한 아이디어를 제공하는 것을 목적으로 제시된다.첫 번째 파트에서는 단일 객관적 최적화 사례에 대한 일부 객관적 기능이 제시된다.두 번째 파트에서는 다중 객체 최적화 문제(MOP)에 대한 각각의 파레토 전선을 이용한 시험 기능이 제공된다.
단일 객관적 최적화 문제에 대해 여기에 제시된 인공적 경관은 Beck,[1] Haupt et al.[2] 및 Rody Oldenhuis 소프트웨어에서 가져온다.[3]문제 수(총 55개)를 감안할 때 여기서는 몇 가지 문제만 제시된다.
MOP에 대한 알고리즘 평가에 사용된 테스트 기능은 [4]Deb, Binh 등, Binh에서 가져갔다.[5][6]GA로 NSA-II 절차를 구현하는 [7]Deb이 개발한 소프트웨어나 ES로 NSA-II 절차를 구현하는 인터넷에 게시된 프로그램을 다운로드할 수 있다.[8]
여기에는 방정식의 일반적인 형태, 목적함수의 플롯, 객체 변수의 경계 및 전역 미니마의 좌표가 제시되어 있다.
단일 객체 최적화를 위한 테스트 함수
| 이름 | 플롯 | 공식 | 글로벌 최소값 | 도메인 검색 |
|---|---|---|---|---|
| 라스트리긴 함수 | 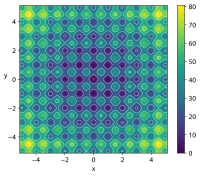 |
| ||
| 애클리 함수 | 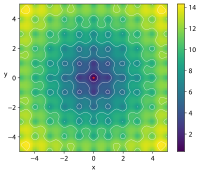 |
| ||
| 구체함수 |  | - i { {{ {\ -}\leq \ ≤ { { { { { { { { { { { { { 1 1 1 111 | ||
| 로젠브록 함수 |  | - i { {{ {\ -}\leq \ ≤ { { { { { { { { { { { { { 1 1 1 111 | ||
| 비일 함수 |  |
| ||
| 골드스타인-프라이스 함수 | 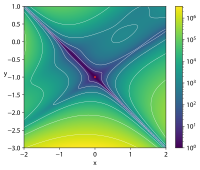 |
| ||
| 부스 함수 |  | |||
| 북인함수 N.6 |  | - x- y | ||
| 마트야스 함수 |  | |||
| 레비 함수 N.13 |  |
| ||
| 힘멜블라우의 기능 | 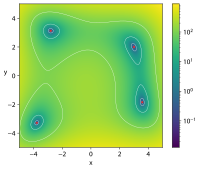 | |||
| 삼점프 낙타 함수 | 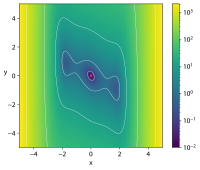 | |||
| 이솜함수 | 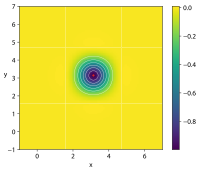 | |||
| 크로스인트레이 함수 |  | |||
| 에그홀더 함수[9] | 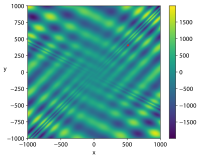 | |||
| 홀더 테이블 함수 |  | |||
| 매코믹 함수 |  | .5 x- y | ||
| 섀퍼 함수 N. 2 | 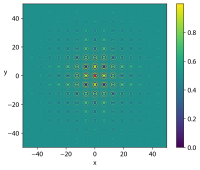 | |||
| 섀퍼 함수 N. 4 |  | |||
| 스티블린스키-탕 함수 | 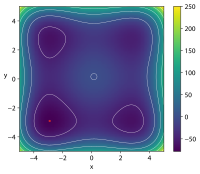 | ≤ {{ { { { { { - - i n { { { { 1 1 1 1 1 1 1 11 1 1 1 11 1 1 |
제한된 최적화를 위한 테스트 함수
| 이름 | 플롯 | 공식 | 글로벌 최소값 | 도메인 검색 |
|---|---|---|---|---|
| 큐빅과 라인으로 제약된 로젠브로크[10] 함수 |  | ( , )=( - ) 2+ - ) 대상: (- 1) 3 -y+ 0 + y- 0 0및 | .5 x 1.1.5- .5 .5 y2.5 | |
| 디스크에[11] 제한된 로젠브록 함수 | 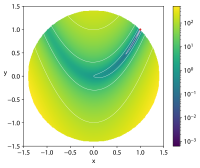 | ( , )=( - ) 2+ - ) 대상: + x} | .5 x.5 1.5 {\.5\ x 1- 1. { 1.5 {\ y1.5 | |
| 미샤의 새 기능 - 제한됨[12][13] |  | , : (x+ ) +( + ) < | ≤ x x- y | |
| 타운젠드 함수(수정)[14] |  | ( x, )=-[ (( x- 0.) ) - ( + ) 대상: x + <[ 2 t - 2 2 t - 2 cos - 4 t - + [ ] ] [\ x^{2]{}:{21}{ t = Atan2(x,y) | 2. x2.25 .25 x2.25 - .5 y | |
| 고메즈 및 레비 함수(수정)[15] |  | , y)= 4 - 2.1 x + 3 + + 1}{14 대상: - ( x)+ ( 2 y) .5 x y1.5 | ≤ - y | |
| 시미오네스쿠 함수[16] |  | ( x, )=.1 대상: 2+ y [ + S ( x ) x} 서 =, S = 0. = 8{\{\{}{}{} |
다중 목적 최적화를 위한 테스트 함수
| 이름 | 플롯 | 기능들 | 제약 | 도메인 검색 |
|---|---|---|---|---|
| 빈 및 코른 함수:[5] | 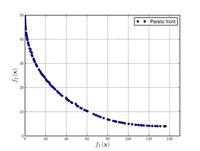 | 3 y | ||
| Chankong 및 Haimes 함수:[17] |  | |||
| 폰세카-플레밍 함수:[18] | 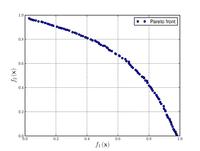 | ≤ 4 i | ||
| 테스트 기능 4:[6] | ![Test function 4.[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Test_function_4_-_Binh.pdf/page1-200px-Test_function_4_-_Binh.pdf.jpg) | |||
| 쿠르사위 함수:[19] | 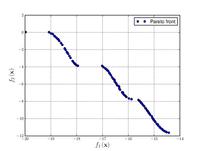 | ≤ 5 3 i | ||
| Schaffer 함수 N. 1:[20] | 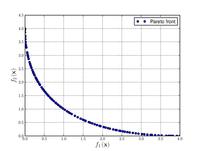 | x ~ A의 값이 성공적으로 사용됨 의 값이 클수록 문제의 난이도가 높아진다. | ||
| Schaffer 함수 N. 2: |  | x. | ||
| 폴로니의 두 가지 객관적인 기능: | 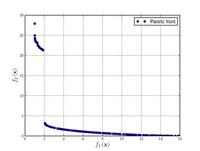 |
| ||
| 지츨러-뎁-Tiele의 함수 N. 1:[21] |  | 1 1 i i | ||
| 지츨러-뎁-Tiele의 함수 N. 2:[21] | 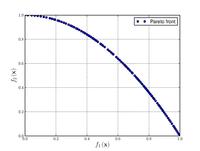 | 1 1 i i | ||
| 지츨러-뎁-Tiele의 함수 N. 3:[21] | 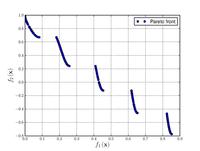 | 1 1 i i | ||
| 지츨러-뎁-Tiele의 함수 N. 4:[21] | 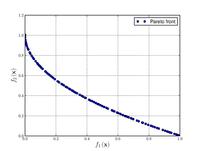 | ≤ - x 5 5 2 i | ||
| 지츨러-뎁-Tiele의 함수 N. 6:[21] |  | 1 1 i | ||
| Osyczka 및 Kundu 함수:[22] | 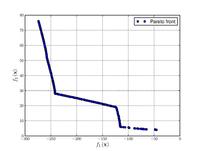 | , , . | ||
| CTP1 함수(2 변수):[4][23] | ![CTP1 function (2 variables).[4]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/CTP1_function_%282_variables%29.pdf/page1-200px-CTP1_function_%282_variables%29.pdf.jpg) | , y 1 . | ||
| 제약-Ex 문제:[4] | ![Constr-Ex problem.[4]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Constr-Ex_problem.pdf/page1-200px-Constr-Ex_problem.pdf.jpg) | .1 0 1 5 y | ||
| Viennet 함수: | 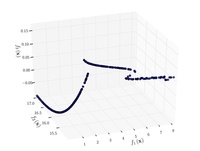 | , . |
참고 항목
| Wikimedia Commons에는 테스트 기능(수학적 최적화)과 관련된 미디어가 있다. |
참조
- ^ Bäck, Thomas (1995). Evolutionary algorithms in theory and practice : evolution strategies, evolutionary programming, genetic algorithms. Oxford: Oxford University Press. p. 328. ISBN 978-0-19-509971-3.
- ^ Haupt, Randy L. Haupt, Sue Ellen (2004). Practical genetic algorithms with CD-Rom (2nd ed.). New York: J. Wiley. ISBN 978-0-471-45565-3.
- ^ Oldenhuis, Rody. "Many test functions for global optimizers". Mathworks. Retrieved 1 November 2012.
- ^ a b c d e Deb, Kalyanmoy(2002) 진화 알고리즘을 사용한 다목적 최적화(Repr. ed.치커스터 [u.a]:와일리, ISBN 0-471-87339-X
- ^ a b Binh T.와 Korn U. (1997) MOBES: 제한된 최적화 문제에 대한 다목적 진화 전략.인: 제3차 유전자 알고리즘 국제회의의 진행.체코어 176-182페이지
- ^ a b c Binh T. (1999) 다목적 진화 알고리즘. 연구 사례.기술 보고서.자동화 통신 연구소.독일 바레벤
- ^ Deb K. (2011) C의 다목적 NSGA-II 코드용 소프트웨어.URL: https://www.iitk.ac.in/kangal/codes.shtml에서 이용 가능
- ^ Ortiz, Gilberto A. "Multi-objective optimization using ES as Evolutionary Algorithm". Mathworks. Retrieved 1 November 2012.
- ^ Vanaret C. (2015) 난해한 최적화 문제 해결을 위한 인터벌 방법과 진화 알고리즘의 하이브리드화.박사 논문.Ecole Nationale de l'Aviation Civille.프랑스 국립 폴리테크니크 드 툴루즈 연구소
- ^ Simionescu, P.A.; Beale, D. (September 29 – October 2, 2002). New Concepts in Graphic Visualization of Objective Functions (PDF). ASME 2002 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Montreal, Canada. pp. 891–897. Retrieved 7 January 2017.
- ^ "Solve a Constrained Nonlinear Problem - MATLAB & Simulink". www.mathworks.com. Retrieved 2017-08-29.
- ^ "Bird Problem (Constrained) Phoenix Integration". Archived from the original on 2016-12-29. Retrieved 2017-08-29.
{{cite web}}: CS1 maint : bot : 원본 URL 상태 미상(링크) - ^ Mishra, Sudhanshu (2006). "Some new test functions for global optimization and performance of repulsive particle swarm method". MPRA Paper.
- ^ Townsend, Alex (January 2014). "Constrained optimization in Chebfun". chebfun.org. Retrieved 2017-08-29.
- ^ Simionescu, P.A. (2020). "A collection of bivariate nonlinear optimisation test problems with graphical representations". International Journal of Mathematical Modelling and Numerical Optimisation. 10 (4): 365–398. doi:10.1504/IJMMNO.2020.110704.
- ^ Simionescu, P.A. (2014). Computer Aided Graphing and Simulation Tools for AutoCAD Users (1st ed.). Boca Raton, FL: CRC Press. ISBN 978-1-4822-5290-3.
- ^ Chankong, Vira; Haimes, Yacov Y. (1983). Multiobjective decision making. Theory and methodology. ISBN 0-444-00710-5.
- ^ Fonseca, C. M.; Fleming, P. J. (1995). "An Overview of Evolutionary Algorithms in Multiobjective Optimization". Evol Comput. 3 (1): 1–16. CiteSeerX 10.1.1.50.7779. doi:10.1162/evco.1995.3.1.1. S2CID 8530790.
- ^ F. Kursawe, PPSN I, Vol 496 Compute Sc의 "벡터 최적화를 위한 진화 전략의 변종".Springer-Verlag, 1991 페이지 193–197.
- ^ Schaffer, J. David (1984). "Multiple Objective Optimization with Vector Evaluated Genetic Algorithms". In G.J.E Grefensette; J.J. Lawrence Erlbraum (eds.). Proceedings of the First International Conference on Genetic Algorithms. OCLC 20004572.
- ^ a b c d e Deb, Kalyan; Thiele, L.; Laumanns, Marco; Zitzler, Eckart (2002). "Scalable multi-objective optimization test problems". Proceedings of the 2002 IEEE Congress on Evolutionary Computation. Vol. 1. pp. 825–830. doi:10.1109/CEC.2002.1007032. ISBN 0-7803-7282-4. S2CID 61001583.
- ^ Osyczka, A.; Kundu, S. (1 October 1995). "A new method to solve generalized multicriteria optimization problems using the simple genetic algorithm". Structural Optimization. 10 (2): 94–99. doi:10.1007/BF01743536. ISSN 1615-1488. S2CID 123433499.
- ^ Jimenez, F.; Gomez-Skarmeta, A. F.; Sanchez, G.; Deb, K. (May 2002). "An evolutionary algorithm for constrained multi-objective optimization". Proceedings of the 2002 Congress on Evolutionary Computation. CEC'02 (Cat. No.02TH8600). 2: 1133–1138. doi:10.1109/CEC.2002.1004402. ISBN 0-7803-7282-4. S2CID 56563996.
![f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa1c38ee739ca9cf4582867d74d469df4676cbc)



![{\displaystyle f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f00d1325d65d088f8ae6a96137e62021107921d)
![{\displaystyle -\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20}](https://wikimedia.org/api/rest_v1/media/math/render/svg/565ef43958a50fb0ef473bdd46e30bfc725604a7)





![{\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64863353dcdea2f0ed049cec3aea0a4284d4916a)





![{\displaystyle f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d020ed324ff07759faf17591157771b0e2cdf07)
![{\displaystyle \left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e562da4f3219f9d66e059441c59e1d299e8557)


















![{\displaystyle f(x,y)=-0.0001\left[\left|\sin x\sin y\exp \left(\left|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|+1\right]^{0.1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d591ae9bcf2feae162cd00398d78bb6870c82946)









![{\displaystyle f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/995008c6f10a14b44dac568cc544efb7d5ddd631)
![{\displaystyle f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left|x^{2}-y^{2}\right|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2458c352c0c0524648d8ef713bcea4e80df32fd8)









![{\displaystyle f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7987d4a794d861e7ccd0795265841d3ca172cfae)



![{\displaystyle f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dac25f97d0b720512d72c313000d5fb5c7d033a)
![{\displaystyle x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57168b192e685c6144e3a9527b12087ac7cb11b4)





![{\displaystyle x^{2}+y^{2}\leq \left[r_{T}+r_{S}\cos \left(n\arctan {\frac {x}{y}}\right)\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc42adcc2095ed0c0214a74799db7ee2fac9923)








![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\f_{2}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113203c5d455e0e1e6397d57094e80e527b34ba)




![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb9856144d9869aae4254892ece0fe894dfc152)







![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ee5df22af124899c1e268325017ea64e517b51e)









![{\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f03bdd2b0c7a5af33b0a0fc385f9a9c021635d6e)
















