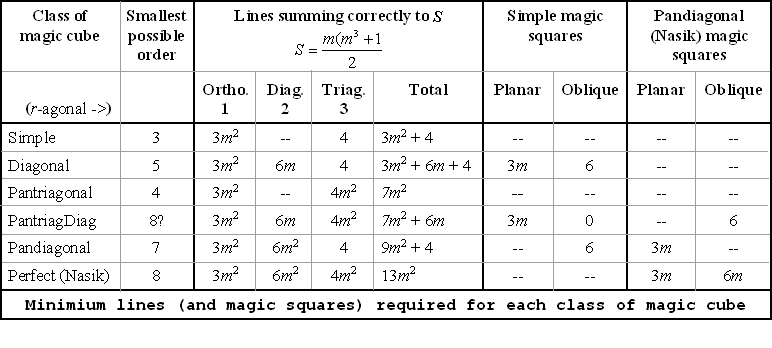
매직 큐브 클래스
Magic cube classes모든 매직 큐브는 큐브 특성에 따라 6개의 매직 큐브 클래스 중 하나에 할당될 수 있다.
이 새로운 시스템은 매직 큐브를 더 정확하게 정의한다.그러나 더 중요한 것은, 마법의 하이퍼큐브의 모든 주문과 모든 차원에 대해 일관성이 있다는 것이다.
큐브가 마법이 되기 위한 최소 요구 사항은 다음과 같다: 모든 행, 기둥, 기둥 및 4개의 3각형을 동일한 값으로 합해야 한다.
6학급
- 단순:
매직 큐브의 최소 요구 사항은 다음과 같다: 모든 행, 기둥, 기둥 및 4개의 3각형을 동일한 값으로 합해야 한다.단순한 마법의 큐브에는 마법의 사각형이 없거나 다음 클래스에 참가하기에 충분하지 않다.
가장 작은 일반적인 간단한 마법 큐브는 순서 3이다.최소 정확한 합계 = 3m2 + 4
- 대각선:
3m 평면 배열은 각각 단순한 마법의 사각형이어야 한다.6개의 사선 사각형도 단순한 마법이다.가장 작은 일반 사선 마법 큐브는 순서 5이다.
이 사각형들은 가드너와 다른 사람들에 의해 '퍼펙트'라고 불렸다!그와 동시에 그는 랭만의 1962년 판디각형 큐브를 '완벽한'이라고도 불렀다.
Christian Boyer와 Walter Trump는 이제 이것과 다음 두 클래스를 Perfect로 간주한다. (아래 대체 Perfect 참조)
A. H. 프로스트는 단순한 클래스를 제외한 모든 클래스를 나식 큐브라고 불렀다.
가장 작은 일반 사선 마법 큐브는 순서 5이다. 사선 마법 큐브를 참조하십시오.최소 정확한 합계 = 3m2 + 6m + 4
- 팬트리각형:
모든 4m2 팬트리곤은 정확하게 합해야 한다(즉, 1-세그먼트, 12(m-1) 2-세그먼트, 4(m-2)(m-1) 3-세그먼트).간단한 AND/OR 판디각형 마법 사각형이 있을 수 있지만 다른 분류를 만족시키기에는 충분하지 않다.
가장 작은 일반 팬트리각형 마법 큐브는 순서 4이다. 팬트리각형 마법 큐브를 참조하십시오.
필요한 최소 합계는 7m이다2.r = 1과 3에 대한 모든 범알-아곤의 합이 정확하다.
- PantriagDiag:
이 등급의 큐브는 나카무라 미쓰토시에 의해 2004년 말에 처음 만들어졌다.이 큐브는 팬트리각형 마법 큐브와 사선 마법 큐브를 결합한 것이다.따라서 모든 주삼각형 및 깨진 삼각형의 합이 정확하며, 3m 평면의 간단한 마법 광장을 포함하고 있다.게다가 6개의 사선 사각형은 모두 범각선 마법 사각형이다.지금까지 만들어진 큐브는 오더8밖에 없다.다른 어떤 주문이 가능한지 알 수 없다. 팬트리아그 매직 큐브를 참조하라.필요한 최소 합계는 7m2 + 6m이다.
- 판디각형:
3m 평면 배열은 모두 판디각형 마법 사각형이어야 한다.6개의 사선 사각형은 항상 마법(대개 간단한 마술)이다.그것들 중 몇 개는 범각선 마법일지도 모른다.가드너는 또한 이것을 '완벽한' 큐브라고 불렀는데, 아마도 마이어의 큐브보다 더 높은 등급이라는 것을 깨닫지 못했을 것이다.이전 노트 르 보이어와 트럼프를 참조하십시오.
가장 작은 일반 판디각형 마법 큐브는 순서 7이다. 판디각형 마법 큐브를 참조하라.
필요한 최소 합계는 9m2 + 4이다.r = 1과 2에 대한 모든 범-알-알-알-알-알-알-알-알-알-알의 합이
- 완벽:
3m 평면 배열은 모두 판디각형 마법 사각형이어야 한다.또한 모든 팬트리곤은 정확하게 합해야 한다.이 두 조건이 합쳐져 총 9m의 판디각형 마법 광장을 제공한다.
가장 작은 일반적인 완벽한 매직 큐브는 순서 8이다; Perfect magic cube를 참조하라.
나식; A.H. 프로스트(1866)는 단순한 마법의 큐브를 제외한 모든 것을 나식이라고 불렀다!
C. Planck(1905)는 Nasik을 가능한 모든 선이 정확하게 요약된 모든 주문이나 치수의 매직 하이퍼큐브를 의미하도록 재정의했다.
즉, 나식(Nasik)은 대체적으로 선호되는 용어로서, 완벽한 클래스를 위한 모호성이 덜하다.
필요한 최소 합계는 13m이다2.r = 1, 2 및 3에 대한 모든 범-알-알-알-알-알-알-알-알-알-알-알-알-알
Alternate Perfect는 위의 내용이 비교적 새로운 완벽의 정의라는 점에 주목한다.1995년경까지 무엇이 완벽한 매직 큐브를 구성했는지에 대해 많은 혼란이 있었다(Allight 아래 토론 참조).
아래에는 이전 정의의 논의에 대한 참조 및 링크가 포함되어 있다.
개인용 컴퓨터의 인기와 함께 마법 큐브의 더 미세한 디테일을 검사하는 것이 더 쉬워졌다.또한 점점 더 많은 작업이 고차원적인 매직 하이퍼큐브에 행해지고 있었다.예를 들어, 존 헨드릭스는 2000년에 세계 최초의 나시크매직 테세락트를 만들었다.헨드릭스 정의에 의해 완벽한 마법의 큐빅으로 분류되었다.
모든 차원에 대해 일반화됨
모든 범n-아곤을 정확하게 합친다면 n차원의 매직 하이퍼큐브는 완벽하다.그러면 그 안에 들어 있는 저차원 하이퍼큐브도 모두 완벽하다.
차원 2에서는 판디각형 마법 광장이 수년 동안 완벽하다고 불려왔다.이것은 큐브에 대해 위에 주어진 완벽한 (Nasik) 정의와 일치한다.이 차원에서는 단순하고 완벽한 두 부류의 마술 사각형만이 존재하기 때문에 애매함이 없다.
4차원의 경우, 마법의 큐브인 나카무라 미쓰토시(中村)는 18개 등급이 있다고 판단했다.그는 그들의 특징을 파악하고 각각의 예를 구성했다.그리고 이 차원에서도 퍼펙트(Nasik) 매직 테세락트는 가능한 모든 선이 정확하게 요약되어 있고 그 안에 포함된 모든 큐브와 사각형 역시 나식 마술이다.
다른 정의 및 표
적정: 적절한 매직 큐브는 6가지 등급의 매직 큐브 중 하나에 속하지만, 그 등급의 매직 큐브에 대한 최소 요구 조건을 정확히 포함하고 있다. 즉, 적절한 단순 또는 팬트리각형 매직 큐브는 매직 사각형을 포함하지 않으며, 적절한 대각선 매직 큐브는 정확히 3m + 6개의 매직 스퀘어를 포함할 것이다.이 용어는 2004년 4월에 나카무라 미쓰토시에 의해 만들어졌다.
표에 대한 참고 사항
- 대각선 또는 대각선 클래스의 경우, 6개의 사선 마법 사각형 중 하나 또는 두 개가 대각선 마법일 수 있다.사선 사각형 중 6개를 제외한 모든 것이 '파쇄'되어 있다.이것은 대각선 마법의 사각형에서 깨진 대각선과 유사하다. 즉, 깨진 대각선은 2-D 사각형에서 1-D이고, 깨진 사선 사각형은 3-D 큐브에서 2-D이다.
- 표에는 각 등급에 필요한 최소 선 또는 정사각형(즉, 적절한)이 표시된다.보통은 더 많지만 다음 수업에 참가하기엔 한 가지 유형이 충분하지 않다.
참고 항목
참조
추가 읽기
- 프로스트, 닥터 A. H. 나식 큐브의 일반적 특성에 관한 연구, QJM 15, 1878, 페이지 93–123
- Planck, C, 경로론 Nasik, 사적 순환을 위해 인쇄된 A.J. Lawrence, 프린터, 럭비, 1905년
- 하인즈, H.D. 그리고 헨드릭스, J. R., 매직 스퀘어 렉시콘:삽화.자체 출판, 2000, 0-9687985-0-0.
- 헨드릭스, 존 R, 팬-4-아곤 매직 테세락트, 미국 수학 월간지, 75권, 1968년 4월, 페이지 384.
- 헨드릭스, 존 R, 팬-3-아곤 매직 큐브, 레크리에이션 수학 저널, 5:1, 1972, pp51–52
- 헨드릭스, 존 R, 주문-5, JRM, 5:3, 1972, pp 205–206의 팬-3-아곤 매직 큐브
- 헨드릭스, 존 R, 컴퓨터 별 테세르텍트행 매직 스퀘어, 1999년 자체 발행. 0-9684700-0-9
- 헨드릭스, 존 R, 오더 2n의 퍼펙트 n차원 매직 하이퍼큐브, 셀프 출판 1999. 0-9684700-4-1
- 클리포드 A. 픽오버(2002년).마법의 광장, 원, 별의 선.프린스턴 유니브프레스, 2002, 0-691-07041-5. 페이지 101–121
외부 링크
큐브 클래스
퍼펙트 큐브
큐세랙트 클래스