구배 지수 광학
Gradient-index opticsGRIN(Gradient-Index) 광학은 재료의 굴절률의 구배에 의해 생성된 광학 효과를 다루는 광학 분야입니다.이러한 점진적인 변화는 평탄한 표면을 가진 렌즈 또는 전통적인 구형 렌즈의 전형적인 수차를 가지지 않는 렌즈를 생산하는 데 사용될 수 있다.구배지수 렌즈는 구면, 축면 또는 방사상의 굴절 구배를 가질 수 있습니다.
자연에서
눈의 렌즈는 자연에서 가장 명백한 구배지수 광학이다.사람의 눈에서 렌즈의 굴절률은 중앙층의 약 1.406에서 [1]렌즈의 밀도가 낮은 층의 약 1.386까지 다양하다.이를 통해 눈은 단거리와 [2]장거리 모두에서 뛰어난 해상도와 낮은 수차로 영상을 촬영할 수 있습니다.
자연경사지수광학의 또 다른 예는 더운 날 도로에 나타나는 물웅덩이의 일반적인 신기루이다.이 수영장은 실제로 하늘의 이미지이며, 정상적인 직선 경로에서 빛이 굴절(굴절)되고 있기 때문에 도로에 있는 것으로 보입니다.이는 도로 표면의 뜨겁고 밀도가 낮은 공기와 그 위의 더 밀도가 높은 차가운 공기 사이의 굴절률의 변화 때문이다.공기의 온도 변화(따라서 밀도)는 굴절률의 구배를 유발하여 [3]높이에 따라 증가시킵니다.이 지수 구배는 하늘에서 (도로에 대한 얕은 각도로) 광선을 굴절시켜 보는 사람의 눈으로 굴절시키고, 그 겉으로 보이는 위치는 도로 표면이다.
지구의 대기는 실제로 수평선 아래에 있는 몇 분 동안 태양을 볼 수 있게 해주는 GREN 렌즈 역할을 하며,[3] 관측자들은 또한 수평선 아래에 있는 별들을 볼 수 있다.이 효과는 또한 무선 엄폐 측정에서와 같이 위성이 수평선 아래로 하강한 후 위성의 전자파 신호를 관찰할 수 있게 한다.
적용들
GRIN 렌즈의 평평한 표면은 렌즈 장착을 용이하게 하기 때문에 복사기나 [4]스캐너와 같이 매우 작은 렌즈를 함께 장착해야 하는 경우에 유용합니다.또한 평평한 표면은 GRIN 렌즈를 광학적으로 섬유에 쉽게 정렬하여 시준된 출력을 생성함으로써 [5]내시경 검사 및 뇌 내 칼슘 이미징 및 광유전자 자극에 적용할 수 있습니다.
영상촬영 어플리케이션에서 GRIN 렌즈는 주로 수차를 줄이기 위해 사용됩니다.이러한 렌즈의 설계에는, 렌즈의 효율적인 제조 뿐만이 아니라, 수차의 상세한 계산도 포함됩니다.GRIN 렌즈에는 광학 안경, 플라스틱, 게르마늄, 셀렌화 아연, [4]염화나트륨 등 다양한 소재가 사용되고 있습니다.
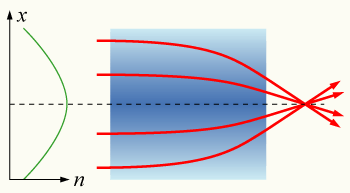
특정 광섬유(그레이드 지수 섬유)는 방사상 가변 굴절률 프로파일을 사용하여 제작됩니다.이 설계는 멀티 모드 광섬유의 모드 분산을 크게 줄입니다.굴절률의 방사상 변화는 섬유 내에서 광선의 사인파 높이 분포를 허용하여 광선이 코어에서 나가는 것을 방지합니다.이는 GRIN 파이버의 모든 모드가 같은 속도로 전파되어 [6]파이버의 시간 대역폭을 높일 수 있다는 점에서 전체 내부 반사에 의존하는 기존 광섬유와는 다릅니다.
반사 방지 코팅은 일반적으로 좁은 주파수 범위 또는 입사 각도에 효과적이다.그레이드 인덱스 재료는 제약이 [7]적습니다.
태양전지에 햇빛을 집중시키기 위해 축방향 구배 렌즈가 사용되어 태양이 최적의 [8]각도에 있지 않을 때 입사광의 90%를 포착했다.
제조하다
GRIN 렌즈는 몇 가지 기술로 제조됩니다.
- 중성자 조사 – 붕소가 풍부한 유리는 붕소 농도의 변화를 일으키기 위해 중성자의 충격을 받아 [6][9]렌즈의 굴절률이 변화한다.
- 화학 증기 증착 – 굴절률이 다양한 여러 유리를 표면에 증착하여 누적 굴절 [6][10]변화를 일으킵니다.
- 부분 중합 – 유기 모노머는 다양한 강도의 자외선을 사용하여 부분적으로 중합되어 굴절 [6][11]구배를 제공합니다.
- 이온 교환 – 유리를 리튬 이온과 함께 액체 용해액에 담급니다.확산에 의해 유리 중의 나트륨 이온이 리튬 이온과 부분적으로 교환되어 가장자리에서 교환량이 많아진다.따라서 샘플은 굴절률의 [6][12]구배 재료 구조와 그에 상응하는 구배를 구한다.
- 이온 스터핑 – 특정 유리의 상분리 때문에 모공이 형성되며, 모공은 나중에 다양한 염분 또는 염분 농도를 사용하여 채워질 수 있습니다.[6][13]
- 직접 레이저 쓰기 – 사전 설계된 구조를 하나하나 노출하는 동안 노출 선량이 변화합니다(스캔 속도, 레이저 전력 등).이는 공간적으로 조정 가능한 단량체 대 중합체 변환도에 대응하여 다른 굴절률을 발생시킨다.이 방법은 자유형 마이크로 광학 소자 및 다성분 [14]광학에 적용할 수 있습니다.
역사
1854년, J C 맥스웰은 굴절률 분포로 우주의 모든 영역을 선명하게 촬영할 수 있는 렌즈를 제안했다.맥스웰 어안 렌즈로 알려진 이 렌즈는 구면 지수 함수를 포함하며 모양도 [15]구면이어야 합니다.그러나 이 렌즈는 표면과 렌즈 내부의 점만 선명하게 촬영되고 확장된 물체는 극심한 이상 현상을 겪기 때문에 실용적이지 않고 실용성도 거의 없다.1905년 R. W. W. Wood는 축으로부터의 반경 거리에 따라 대칭적으로 변화하는 굴절률 구배를 가진 젤라틴 원통을 만드는 침지 기술을 사용했다.실린더의 원반 모양의 슬라이스는 나중에 방사형 지수 분포가 있는 평면면을 가진 것으로 나타났다.그는 렌즈의 표면이 평평하더라도 지수가 반지름 [16]거리에 비해 감소하는지 증가하는지 여부에 따라 수렴 및 분산 렌즈와 같은 역할을 한다는 것을 보여주었다.1964년, R. K. 뤼네부르크의 사후 책은 그가 입사한 평행한 [17]빛의 광선을 렌즈의 반대쪽 표면에 있는 한 점에 초점을 맞추는 렌즈를 기술한 것을 출판했다.이것은 또한 가시광선의 초점을 맞추기 위해 렌즈를 사용하는 것이 어려웠기 때문에 렌즈의 적용을 제한했지만, 마이크로파 적용에서는 어느 정도 유용했습니다.몇 년 후, Wood 타입의 렌즈를 제작하기 위한 몇 가지 새로운 기술이 개발되었습니다.그 이후로 적어도 얇은 GRIN 렌즈는 매우 단순한 기계적 구조를 고려할 때 놀라울 정도로 좋은 이미징 특성을 가질 수 있으며, 두꺼운 GRIN 렌즈는 예를 들어 Selfoc [18]로드에 적용되었습니다.
이론.
불균일 경사지수 렌즈는 매체 내 관심 영역의 좌표 함수 n 에 변화 굴절률을 가진다.페르마의 원리에 따르면 광로 적분(L)은 매체의 어떤 두 점을 접합하는 광선을 따라 두 점을 접합하는 어떤 인근 곡선의 값에 대해 정지되어 있다.광로 적분은 다음 식에 의해 주어진다.
- S s \ L = \_ { _ { } ^{ } , ds。여기서 n은 굴절률, S는 곡선의 호 길이이다.데카르트 좌표를 사용하는 경우, 이 방정식은 각 물리적 치수에 대한 구형 구배에서의 호 길이 변화를 통합하도록 수정된다.
여기서 prime은 d/[19]ds에 해당합니다.광로 적분은 렌즈를 통과하는 빛의 경로를 질적으로 특징지을 수 있어 향후 렌즈가 쉽게 재현될 수 있습니다.
GRIN 렌즈의 굴절률 구배는 사용된 생산 방법에 따라 수학적으로 모델링할 수 있습니다.예를 들어,[20] SELFOC Microlens와 같은 방사형 구배 지수 재료로 만들어진 GRIN 렌즈의 굴절률은 다음에 따라 달라집니다.
- r (1 - }=left 여기서 n은r 광축으로부터의 거리에서의 굴절률, n은o 광축상의 설계지수, A는 양의 상수이다.
「 」를 참조해 주세요.
레퍼런스
- ^ Hecht, Eugene; Zając, Alfred (1987). Optics (2nd ed.). Reading, Mass.: Addison-Wesley. p. 178. ISBN 978-0201116090. OCLC 13761389.
- ^ Shirk J S, Sandrock M, Scribner D, Fleet E, Stroman R, Baer E, Hiltner A. (2006) NRL 검토 페이지 53-61
- ^ a b Tsiboulia, A B(2003)."GRIN(Gradient Index) 렌즈"로널드 G. 드러거스에서요광학공학 백과사전 제1권뉴욕, 뉴욕: 마르셀 데커, 675-683ISBN 9780824742508.
- ^ a b "Gradient Index Lenses Selection Guide: Types, Features, Applications". Engineering360. Retrieved 2021-07-11.
- ^ "In Vivo Calcium Imaging: The Ultimate Guide". Mightex. 2019. Retrieved 2021-07-11.
- ^ a b c d e f Moore, Duncan T. (1980). "Gradient-index optics: a review". Applied Optics. 19 (7): 1035–1038. doi:10.1364/AO.19.001035.
- ^ Zhang, Jun-Chao; Xiong, Li-Min; Fang, Ming; He, Hong-Bo (2013). "Wide-angle and broadband graded-refractive-index antireflection coatings" (PDF). Chinese Physics B. 22 (4): 044201. Bibcode:2013ChPhB..22d4201Z. doi:10.1088/1674-1056/22/4/044201. Retrieved 13 May 2016.
- ^ Irving, Michael (2022-06-28). "Pyramid lenses catch light from any angle to boost solar cell efficiency". New Atlas. Retrieved 2022-06-28.
- ^ 시나이 P(1970).Applied Optics 10, 99-104
- ^ Keck D B와 Olshansky R, "Optimal Index Gradient를 가진 광학 도파관", 미국 특허 3,904,268(1975년 9월 9일).
- ^ 무어 RS, "굴절률 구배를 가진 플라스틱 광학 소자", 미국 특허 371만8383(1973년 2월).
- ^ Hensler J R, "유리에서 굴절률 구배를 생성하는 방법", 미국 특허 3,873,408(1975년 3월 25일).
- ^ Mohr, R K; Wilder, J A; Macedo, P B; Gupta, P K (1979). "Graded index lenses by the molecular stuffing process". A digest of technical papers presented at the Topical Meeting on Gradient Index Optical Imaging Systems, May 15-16, 1979, Rochester, New York. paper WA1. Washington, D C: Optical Society of America. OCLC 489755284.
- ^ Zukauskas, Albertas; Matulaitiene, Ieva; Paipulas, Domas; Niaura, Gedinimas; Malinauskas, Mangirdas; Gadonas, Roaldas (2015). "Tuning the refractive index in 3D direct laser writing lithography: towards GRIN microoptics". Laser & Photonics Reviews. 9 (6): 706–712. Bibcode:2015LPRv....9..706Z. doi:10.1002/lpor.201500170.
- ^ Maxwell, James Clerk (1854). "Solutions of problems: (prob. 3, vol. VIII. p. 188)". The Cambridge and Dublin Mathematical Journal. 9: 9–11. (참조자: )
- ^ Wood, Robert Williams (1905). Physical Optics. New York; London: Macmillan. p. 71.
- ^ Luneburg, Rudolf Karl (1964). Mathematical Theory of Optics. Berkeley: University of California Press. ISBN 978-0-5203-2826-6. OCLC 1149437946.
- ^ Marchand, E.W. (1976). "Third-order aberrations of the photographic Wood". Journal of the Optical Society of America. 66 (12): 1326–1330. doi:10.1364/JOSA.66.001326.
- ^ Marchand, Erich W. (1978). Gradient index optics. New York: Academic Press. ISBN 978-0124707504. OCLC 4497777.
- ^ Flores-Arias, M.T.; Bao, C.; Castelo, A.; Perez, M.V.; Gomez-Reino, C. (2006-10-15). "Crossover interconnects in gradient-index planar optics". Optics Communications. 266 (2): 490–494. Bibcode:2006OptCo.266..490F. doi:10.1016/j.optcom.2006.05.049. ISSN 0030-4018.