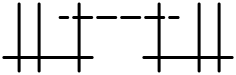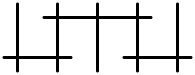타원면

수학에서 타원형 표면은 타원형 진동이 있는 표면으로, 다시 말해서 거의 모든 섬유들이 제1의 매끄러운 곡선이 되도록 대수곡선에 섬유들을 연결한 적절한 형태론이다.(복잡한 숫자와 같이 대수적으로 닫힌 장 위에, 이 섬유들은 아마도 선택된 기원이 없는 타원형 곡선이다.)이것은 속 1의 부드러운 곡선이 되는 일반 섬유와 같다.이것은 적절한 기저 변화에서 비롯된다.

표면과 베이스 곡선은 비곡선(복합 다지관 또는 맥락에 따라 규칙적인 구성)으로 가정한다.타원곡선이 아닌 섬유는 단수섬유라 불리며 고다이라 구니히코에 의해 분류되었다.타원형 섬유와 단수형 섬유 모두 끈 이론, 특히 F 이론에서 중요하다.

타원형 표면은 표면의 많은 흥미로운 예를 포함하고 있는 넓은 부류의 표면을 형성하며, 복잡한 다지관과 매끄러운 4-매니폴드의 이론에서 비교적 잘 이해된다.그것들은 숫자 필드 위에 타원형 곡선과 유사하다.

예

• 곡선이 있는 타원곡선의 산물은 타원 표면(단수 섬유가 없는)이다.
• 고다이라 치수 1의 모든 표면은 타원형 표면이다.
• 모든 복잡한 Enrique 표면은 타원형이며 투영 선 위에 타원형 진동이 있다.
• 고다이라 표면
• 돌가초프 표면
• 시오다 모듈식 표면

고다이라의 단수섬유표

타원형 진동의 섬유는 대부분 (비노래형) 타원형 곡선이다.남아 있는 섬유들을 단수섬유라고 한다. 단수섬유라고 한다. 단수섬유의 수는 유한하며, 단수성 또는 0이 아닌 승수를 가진 합리적 곡선의 조합으로 구성된다(그래서 섬유는 비축소성 계통일 수 있다).고다이라와 네론은 가능한 섬유를 독립적으로 분류했고, 테이트의 알고리즘을 사용하여 숫자장 위에 있는 타원곡선의 섬유의 종류를 찾을 수 있다.

다음 표에는 최소 타원형 진동의 가능한 섬유들이 나열되어 있다. ("소형"은 "소형"을 통해 인수될 수 없는 섬유들을 의미한다. 정확히 말하면, 단수 섬유들은 자기 절개 번호 -1로 매끄러운 이성적 곡선을 포함하지 않아야 한다.)다음과 같은 이점을 제공한다.

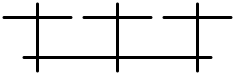
• 고다이라의 섬유 상징,
• 안드레 네론의 섬유 상징은
• 섬유에서 복구할 수 없는 성분 수(타입 I을₀ 제외한 모든 합리적)
• 성분의 교차로 행렬.이것은 1×1 영 매트릭스 또는 아핀 카르탄 매트릭스 중 하나로, Dynkin 도표가 주어진다.
• 각 섬유의 승수는 Dynkin 도표에 표시된다.

고다이라	네론	구성 요소들	교차로 행렬	딘킨 도표	섬유
I0	A	1(시크어)	0
I1	B1	1 (이중 포인트 포함)	0
I2	B2	2(2개의 개별 교차점)	A을1 붙이다
Iv (v≥2)	Bv	v(v 고유 교차점)	A을v-1 붙이다
mIv (v≥0, m≥2)		Iv with multiplicity m
II	C1	1 (정지 포함)	0
III.	C2	2(순서 1개 지점에 위치)	A을1 붙이다
IV	C3	3 (모두 1점에서 만나다)	A을2 붙이다
I0*	C4	5	D를4 붙이다
Iv* (v≥1)	C5,v	5+v	D를4+v 붙이다
IV*	C6	7	E를6 붙이다
III*	C7	8	E를7 붙이다
II*	C8	9	E를8 붙이다

이 표는 다음과 같이 찾을 수 있다.기하학적 인수는 섬유 성분의 교차 행렬이 음의 세미데마인이트여야 하고, 연결되고, 대칭이어야 하며, -1(최소성 기준)과 같은 대각선 항목이 없어야 한다는 것을 보여준다.그러한 행렬은 타입 ADE의 아핀 Dynkin 다이어그램의 카르탄 행렬의 0 또는 배수여야 한다.

교차로 행렬은 다음과 같은 세 가지 예외를 가진 섬유 유형을 결정한다.

• 교차로 행렬이 0이면 섬유는 타원 곡선(타입₀ I)이거나 이중 점(타입₁ I) 또는 정점(타입 II)일 수 있다.
• 교차로 행렬이 A를₁ 부착하는 경우 교차로 다중성 2를 갖는 2개의 구성요소가 있다.이들은 순서 1(타입₂ I)으로 2점 또는 순서 2(타입 III)로 한 지점에서 만날 수 있다.
• 교차로 행렬이 A에₂ 해당하는 경우, 각각 다른 두 개의 요소를 만족하는 3개의 구성요소가 있다.그들은 3개의 구별되는 지점(타입₃ I)에서 쌍으로 만날 수 있고, 또는 모두 같은 지점에서 만날 수 있다(타입 IV).

모노드로미

각 단수 섬유 주변의 모노드로미는 결정인자 1을 갖는 2×2 정수 행렬의 그룹 SL(2,Z)에서 잘 정의된 결합 등급이다.모노드로미는 우리가 단수섬유를 돌면서 매끄러운 섬유(Z에² 이형성)의 첫 번째 호몰로지 집단이 변화하는 방식을 설명한다.단수 섬유와 관련된 이러한 결합 등급의 대표자는 다음과 같다.^[1]

섬유	교차로 행렬	모노드로미	J자리의	부드러운 위치의 그룹 구조
Iν	A을ν-1 붙이다	${\displaystyle {\pmatrix}1&\nu \\0&1\end{pmatrix}}$	$\displaystyle \infit }$	${\displaystyle \mathbf {Z} /\nu \time \mathbf {C} ^*}$
II	0	${\displaystyle {\pmatrix}1&1\\-1&0\end{pmatrix}}$	0	${\displaystyle \mathbf {C} }$
III.	A을1 붙이다	${\displaystyle {\pmatrix}0&1\\-1&0\end{pmatrix}}$	1728	${\displaystyle \mathbf {Z} /2\times \mathbf {C} }$
IV	A을2 붙이다	${\displaystyle {\pmatrix}0&1\\-1\end{pmatrix}}$	0	${\displaystyle \mathbf {Z} /3\times \mathbf {C} }$
I0*	D를4 붙이다	${\displaystyle {\pmatrix}-1&0\\0&#1\end{pmatrix}}$	$C{\displaystyle \mathbf{}}$ ${\$에서	${\displaystyle(\mathbf {Z} /2)^{2}\times \mathbf {C}}$
Iν* (ν1)	D를4+ν 붙이다	${\displaystyle {\pmatrix}-1&-\nu \\0&-1\end{pmatrix}}$	$\displaystyle \infit }$	${\displaystyle (Z\mathbf{}}$/ ${\displaystyle 2\mathrm{}{}^{}}$) ${\displaystyle {2\mathrm{}}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle C\mathbf{}}$ ${\$가) 짝수일 $경우$ Z${\displaystyle }$/ ${\displaystyle 4\mathrm{}}$ ${\displaystyle \times }$ ${\displaystyle C\mathbf{}}$ ${\$
IV*	E를6 붙이다	${\displaystyle {\pmatrix}-1&-1\1&0\end{pmatrix}}$	0	${\displaystyle \mathbf {Z} /3\times \mathbf {C} }$
III*	E를7 붙이다	${\displaystyle {\pmatrix}0&-1\\1&0\end{pmatrix}}$	1728	${\displaystyle \mathbf {Z} /2\times \mathbf {C} }$
II*	E를8 붙이다	${\displaystyle {\pmatrix}0&-1\\1&1\end{pmatrix}}$	0	${\displaystyle \mathbf {C} }$

타입 II, III, IV, I₀^*, IV^*, III^* 또는 II의^* 단수 섬유의 경우, 모노드로미는 SL(2,Z)의 순서가 유한하다.이는 타원형 진동이 그러한 섬유에서 잠재적인 선량을 감소시킨다는 사실을 반영한다.즉, 베이스 곡선의 래미티드 유한 피복 후 단수섬유는 매끄러운 타원곡선으로 대체될 수 있다.부드러운 곡선이 나타나는 것은 표의 j-invariant에 의해 설명된다.복잡한 숫자에 걸쳐, j-invariant 0이 있는 곡선은 순서 6의 자동형성 집단을 갖는 고유한 타원곡선이고, j-invariant 1728이 있는 곡선은 순서 4. (다른 모든 타원곡선은 순서 2의 자동형 집단을 가진다.)

자코비안 타원 진동이라고 불리는 단면을 가진 타원형 진동의 경우, 각 섬유체의 매끄러운 진동은 그룹 구조를 가지고 있다.단수 섬유의 경우, 기초장이 복잡한 숫자라고 편의상 평활 로커스의 이 그룹 구조가 표에 설명되어 있다. (부호 Dynkin 다이어그램${\displaystyle \stackrel{}{}}\gamma {\displaystyle \stackrel{}{\mathrm{}}}$ ~ ${\$에 의해 주어진 교차로 행렬이 있는 단수 섬유에 대하여$,$ 평활 로커스의 이소몰피 성분들의 그룹.c 여기에 나열된 Dynkin 다이어그램 $\gamma {\displaystyle \mathrm{}}$ ${\displaystyle \Gamma }$과(와$)$ 단순하게 연결된 단순 Lie 그룹의 중앙으로.단수 섬유의 그룹 구조를 알면 타원형 진동(섹션 그룹)의 Mordell-Weil 그룹, 특히 비틀림 서브그룹의 계산에 유용하다.

로그 변환

타원 표면 또는 진동의 로그 변환(중앙 p를 갖는 순서 m)은 염기 공간의 점 p를 통해 1의 다중성 섬유로 변한다.역전될 수 있기 때문에 고다중성의 섬유는 모두 다중성 1의 섬유로 변질될 수 있으며, 이것은 모든 다중섬유를 제거하는 데 사용될 수 있다.

로그 변환은 상당히 폭력적일 수 있다. 코다이라 치수를 바꿀 수 있고 대수 표면을 비알골 표면으로 바꿀 수 있다.

예: L을 C의 격자 Z+iZ로 하고 E를 타원 곡선 C/L로 한다.그러면 E×C에서 C까지의 투영 지도가 타원형 진동이 된다.우리는 0 이상의 섬유소를 어떻게 다중성 2의 섬유로 교체하는지를 보여줄 것이다.

(c,s)를 (c+1/2, -s)에 매핑하는 순서 2의 E×C의 자동형이 있다.우리는 X를 이 집단행동에 의해 E×C의 몫이 되게 했다.우리는 (c,s)를 s에² 매핑하여 X를 C 위에 섬유 공간으로 만든다.우리는 (c,s)를 (c-log(s)/2ii,s²)로 매핑하여 X에서 0을 초과하는 섬유에서 0을 뺀 E×C까지 이형성을 구축한다.(0 이상의 두 섬유는 비이형 타원곡선이기 때문에, 진동 X는 확실히 C 전체에 걸쳐 진동 E×C에 이형성이 없다.)

그러면 진동 X는 2와 0의 다중의 섬유질을 가지고 있고, 그렇지 않으면 E×C처럼 보인다.X는 중심 0의 E×C에 순서 2의 로그 변환을 적용하여 얻는다고 한다.

참고 항목

• 엔리케스-고다이라 분류
• 네론 미니멀 모델

메모들

참조

• Barth, Wolf P.; Hulek, Klaus; Peters, Chris A.M.; Van de Ven, Antonius. Compact Complex Surfaces. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. Vol. 4 (2nd enlarged ed.). Berlin: Springer-Verlag. ISBN 3-540-00832-2. Zbl 1036.14016.
• Cossec, François; Dolgachev, Igor. Enriques Surfaces. Boston: Birkhäuser. ISBN 3-7643-3417-7. MR 0986969.
• Kodaira, Kunihiko (1964). "On the structure of compact complex analytic surfaces. I". Am. J. Math. 86: 751–798. doi:10.2307/2373157. Zbl 0137.17501.
• Kodaira, Kunihiko (1966). "On the structure of compact complex analytic surfaces. II". Am. J. Math. 88: 682–721. doi:10.2307/2373150. Zbl 0193.37701.
• Néron, André (1964). "Modèles minimaux des variétés abéliennes sur les corps locaux et globaux". Publications Mathématiques de l'IHÉS (in French). 21: 5–128. doi:10.1007/BF02684271. MR 0179172. Zbl 0132.41403.