주파수 응답 경계
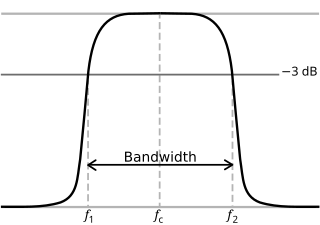
3dB 하한 컷오프1 주파수 f와 3dB 상한 컷오프 주파수2 f를 갖는 밴드패스 필터의 진폭 전달 함수 물리 및 전기공학에서 컷오프 주파수, 코너 주파수 또는 브레이크 주파수는 시스템을 통과하는 에너지가 아니라 감소하기 시작하는(감쇠 또는 반사) 시스템 주파수 응답의 경계입니다.
일반적으로 필터 및 통신 채널과 같은 전자 시스템에서 컷오프 주파수는 로우패스, 하이패스, 밴드패스 또는 밴드스톱 특성(패스밴드와 스톱밴드 사이의 경계를 특징짓는 주파수)의 에지에 적용됩니다.예를 들어, 트랜지션 대역과 패스 밴드가 만나는 필터 응답의 포인트가 되는 경우가 있습니다(회로의 출력이 공칭 패스 밴드 값의 -3 dB인 주파수).또는 트랜지션 대역과 스톱 밴드가 만나는 지점, 예를 들어 30dB 또는 100dB의 감쇠가 필요한 스톱 밴드 감쇠보다 큰 주파수로서 스톱 밴드 코너 주파수를 지정할 수 있다.
도파관 또는 안테나의 경우 컷오프 주파수는 하한 및 상한 컷오프 파장에 대응한다.
일렉트로닉스
전자제품에서 컷오프 주파수 또는 코너 주파수는 회선, 앰프 또는 전자 필터와 같은 회로의 출력이 패스 밴드 내 전력의 특정 비율로 떨어진 주파수입니다.대부분의 경우 이 비율은 패스밴드 전력의 절반입니다.이 비율은 3dB의 강하는 약 절반의 전력에 해당하기 때문에 3dB 포인트라고도 불립니다.전압비율로는 [1]패스밴드전압의1/.로 떨어집니다3dB 지점 이외의 다른 비율도 관련이 있을 수 있습니다(예: 아래 체비셰프 필터 참조).
떨어집니다3dB 지점 이외의 다른 비율도 관련이 있을 수 있습니다(예: 아래 체비셰프 필터 참조).
단극 전달 함수 예제
가장 단순한 저역 통과 필터의 전송 함수,


컷오프시

따라서 컷오프 주파수는 다음과 같이 지정됩니다.

여기서 s는 s-플레인 변수, θ는 각 주파수, j는 가상 단위입니다.
체비셰프 필터
때로는 다른 비율이 3dB 포인트보다 더 편리할 수 있습니다.예를 들어 체비셰프 필터의 경우 일반적으로 컷오프 주파수를 통과 대역 리플의 설계 값으로 레벨이 떨어진 주파수 응답의 마지막 피크 이후의 포인트로 정의합니다.이 필터 클래스의 리플 양은 설계자가 원하는 값으로 설정할 수 있으므로 사용되는 비율은 임의의 값이 [2]될 수 있습니다.
무선 통신
무선통신에서, 하늘파 통신은 전파가 하늘로 비스듬히 전송되어 전리층에 있는 하전입자 층에 의해 지구로 반사되는 기술이다.이 맥락에서 컷오프 주파수라는 용어는 최대 사용 가능한 주파수, 즉 층으로부터의 반사에 의한 2개의 특정 지점 간의 전송에 필요한 입사각에서 전파가 전리층에서 반사되지 않는 주파수를 말한다.
도파관
전자 도파관의 차단 주파수는 모드가 전파되는 최소 주파수입니다.광섬유에서는 광섬유 또는 도파관에서 전파되는 최대 파장인 컷오프 파장을 고려하는 것이 일반적입니다.차단 주파수는 전자파에 대한 헬름홀츠 방정식의 특성 방정식으로 구할 수 있는데, 이는 종파수를 0으로 설정하고 주파수를 푸는 방식으로 전자파 방정식에서 도출된다.따라서 컷오프 주파수보다 낮은 여자 주파수는 전파가 아니라 감쇠합니다.다음 도출은 무손실 벽을 가정한다.빛의 속도인 c 값은 도파관을 채우는 모든 재료에서 빛의 군속도로 간주해야 한다.
직사각형 도파관의 경우 컷오프 주파수는 다음과 같습니다.

 직사각형의 a {
직사각형의 a {  및 b { b 변
및 b { b 변 모드 번호입니다.TE 모드의 m, 0 { m , \ 0
모드 번호입니다.TE 모드의 m, 0 { m , \ 0 ( { m =n = n =}은
( { m =n = n =}은 허용되지 않습니다). TM 의 경우 m 1 { m 1
허용되지 않습니다). TM 의 경우 m 1 { m 1 } 입니다.
} 입니다.원형 단면의 도파관(각도의존성이 없고 반지름의존성이 가장 낮은 횡자기 모드)에서 TM01 모드의 차단 주파수(우성 모드11 TE 다음으로 높음)는 다음과 같이 주어진다.

 r {\r}은 도파관의 반지름이며, 01(\ \
r {\r}은 도파관의 반지름이며, 01(\ \ })은 0(의 첫 번째 루트(\displaystyle
})은 0(의 첫 번째 루트(\displaystyle  이며, 첫 번째 종류의 순서 1의 베셀 함수입니다.
이며, 첫 번째 종류의 순서 1의 베셀 함수입니다.지배 모드11 TE 컷오프 주파수는 다음과 같습니다[3].

단, 원형 단면 [4]도파관 내부에 배플을 도입함으로써 우위 모드 컷오프 빈도를 줄일 수 있다.싱글 모드 광섬유의 경우 컷오프 파장은 정규화된 주파수가 약 2.405인 파장입니다.
수학적 해석
시작점은 파동 방정식(Maxwell 방정식에서 파생됨)입니다.



 세로 방향의 벡터 성분이 없는 필드(전계 또는 자기장)를 가리킵니다. 즉, "횡" 필드입니다.두 필드 중 적어도 하나가 횡단하는 것은 전자 도파관의 모든 고유 모드의 특성입니다.z축은 도파관의 축을 따르도록 정의됩니다.
세로 방향의 벡터 성분이 없는 필드(전계 또는 자기장)를 가리킵니다. 즉, "횡" 필드입니다.두 필드 중 적어도 하나가 횡단하는 것은 전자 도파관의 모든 고유 모드의 특성입니다.z축은 도파관의 축을 따르도록 정의됩니다. 그 Laplacian의"세로"파생 상품 더 폼의 유일한 기능을 고려하여 줄일 수 있다.

 세로 파형 번호이며, 결과적으로
세로 파형 번호이며, 결과적으로





 전파와 감쇠 사이의 임계 주파수로, {\}}가
전파와 감쇠 사이의 임계 주파수로, {\}}가 0인 주파수에 해당합니다.에 의해 주어집니다.
0인 주파수에 해당합니다.에 의해 주어집니다.
「 」를 참조해 주세요.
레퍼런스
외부 링크

 이 문서에는 General Services Administration 문서의 퍼블릭 도메인 자료가 포함되어 있습니다(MIL-STD-188 지원).
이 문서에는 General Services Administration 문서의 퍼블릭 도메인 자료가 포함되어 있습니다(MIL-STD-188 지원).
 떨어집니다
떨어집니다

















 세로 방향의 벡터 성분이 없는 필드(전계 또는 자기장)를 가리킵니다. 즉, "횡" 필드입니다.두 필드 중 적어도 하나가 횡단하는 것은 전자 도파관의 모든 고유 모드의 특성입니다.z축은 도파관의 축을 따르도록 정의됩니다.
세로 방향의 벡터 성분이 없는 필드(전계 또는 자기장)를 가리킵니다. 즉, "횡" 필드입니다.두 필드 중 적어도 하나가 횡단하는 것은 전자 도파관의 모든 고유 모드의 특성입니다.z축은 도파관의 축을 따르도록 정의됩니다. 
 세로
세로 





 전파와 감쇠 사이의 임계 주파수로,
전파와 감쇠 사이의 임계 주파수로, 


