사각형의 원 패킹

정사각형의 원 패킹은 적용 수학에서 패킹 문제로, 여기서 목적은 가능한 가장 작은 정사각형 안에 단위 원 n개를 넣는 것이다. 또는 동등하게 단위 사각형에 n개의 점을 배열하여 점 사이의 최소 분리, d를_n 얻는 것을 목표로 한다.^[1] 이 두 가지 문제 공식 사이에서 변환하기 위해 단위 원의 사각형은 L${\displaystyle }$= ${\displaystyle 2}$+ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{n_{}}{}}$ ${\$이(가) 될 것이다$.$

솔루션(꼭 최적일 필요는 없음)은 모든 N$10,000에 대해 계산되었다.^[2] N=20까지의 솔루션은 다음과 같다.^[2]

원수(n)	정사각형 크기(측면 길이(L))	dn[1]	수밀도(n/L^2)	피겨
1	2	∞	0.25
2	${\displaystyle 2+{\sqrt{2}}$ ≈ 3.414...	${\displaystyle {\sqrt{2}}$ ≈ 1.414...	0.172...
3	${\displaystyle 2+{\frac {\sqrt{2}}:{2}}+{\frac {\sqrt{6}}{2}}:}$ ≈ 3.931...	${\displaystyle {\sqrt{6}-{\sqrt{2}}$ ≈ 1.035...	0.194...
4	4	1	0.25
5	${\displaystyle 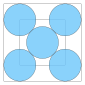2+2{\sqrt{2}}$ ≈ 4.828...	${\displaystyle {\frac {\sqrt{2}}:}$ ≈ 0.707...	0.215...
6	${\displaystyle 2+{\frac {12}{\sqrt{13}}}}}$ ≈ 5.328...	${\displaystyle {\frac {\sqrt{13}{6}}$ ≈ 0.601...	0.211...
7	${\displaystyle 4+{\sqrt{3}}$ ≈ 5.732...	${\displaystyle 4-2{\sqrt{3}}$ ≈ 0.536...	0.213...
8	${\displaystyle 2+{\sqrt{2}}+{\sqrt{6}}}$ ≈ 5.863...	${\displaystyle {\frac {\sqrt{6}}{2}}-{\frac {\sqrt{2}}:}}$ ≈ 0.518...	0.233...
9	6	0.5	0.25
10	6.747...	0.421... OEIS: A281065	0.220...
11	${\displaystyle 3+{\sqrt{2}}+{\frac{6}}{{2}}+{\sqrt{2+4{\sqrt{2}}:}}}}$ ≈ 7.022...	0.398...	0.223...
12	${\displaystyle 2+15{\sqrt{\frac {2}{17}}}}}$ ≈ 7.144...	${\displaystyle {\frac {\sqrt {34}{15}}$ ≈ 0.389...	0.235...
13	7.463...	0.366...	0.233...
14	${\displaystyle 6+{\sqrt{3}}$ ≈ 7.732...	${\displaystyle {\frac {8}{13}-{\frac {2}\sqrt{3}{13}}}}$ ≈ 0.349...	0.226...
15	${\displaystyle 4+{\sqrt{2}}+{\sqrt{6}}}$ ≈ 7.863...	${\displaystyle {\frac {1}{1}:{2}}: {\frac {\sqrt{2}}-{\frac {\sqrt{3}}:{2}}:}$ ≈ 0.341...	0.243...
16	8	0.333...	0.25
17	8.532...	0.306...	0.234...
18	${\displaystyle 2+{\frac {24}{\sqrt{13}}}}}}$ ≈ 8.656...	${\displaystyle {\frac {\sqrt{13}{12}}$ ≈ 0.300...	0.240...
19	8.907...	0.290...	0.240...
20	${\displaystyle {\frac{130}{17}}+{\frac {16}{17}}{\sqrt{2}}}$ ≈ 8.978...	${\displaystyle {\frac {3}{8}-{\frac {\sqrt{2}}{16}}}$ ≈ 0.287...	0.248...

분명한 정사각형 패킹은 1, 4, 9, 16, 25, 36개의 원(최소 6개의 정사각형 수)에 최적이지만 49개 이후부터는 더 큰 정사각형에 최적화가 중단된다.^[2]

사각형이나 다른 직사각형의 밀집된 원들이 많은 조사의 대상이 되어 왔다.^[3]

참조

이 초등 기하학 관련 기사는 단조롭다. 위키피디아를 확장하여 도울 수 있다.

• v
• t