균형유동
Balanced flow이 글은 검증을 위해 인용구가 추가로 필요하다.– · · 책· · (2018년 9월)(이 템플릿 |
대기 과학에서 균형 잡힌 흐름은 대기 운동의 이상화다. 이상화는 일정한 밀도를 갖는 한 고립된 공기의 구획의 거동, 그것에 작용하는 선택된 힘에 따라 수평면에서의 움직임, 그리고 마지막으로 정상 상태 조건을 고려하는 데 있다.
균형 잡힌 흐름은 종종 실제 흐름의 정확한 근사치로, 대기 운동에 대한 질적 이해와 해석을 개선하는 데 유용하다. 특히, 균형 잡힌 흐름 속도는 지구 표면의 대기압의 특정한 배치에 대한 풍속의 추정치로 사용될 수 있다.
자연좌표에서의 운동방정식
궤도
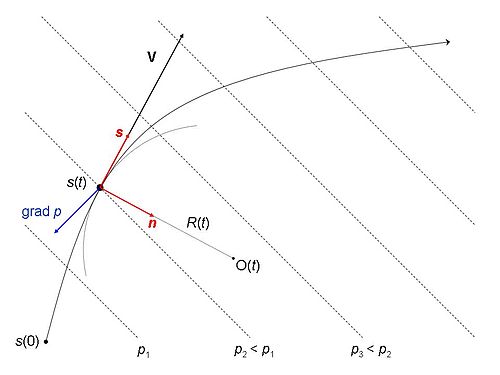
운동량 방정식은 주로 수평면에서 이동하는 흐름의 일반적인 궤적을 위해 작성되며 t라고 불리는 특정 경과 시간에 취해진다. 패킷의 위치는 시간 t로 이동한 궤적 s=s(t)의 거리로 정의된다. 그러나 실제로는 그 궤적이 입자에 대한 힘의 균형의 결과물이다. 이 절에서는 표현의 편의를 위해 처음부터 알고 있다고 가정한다. 다음에 선택한 힘에 의해 결정된 운동을 고려할 때, 우리는 어떤 종류의 궤적이 특정한 힘의 균형에 맞는지 단서를 얻을 것이다.
위치 s에서의 궤적은 항상 s의 성장 방향을 가리키는 하나의 접선 단위 벡터 s와 곡률 O의 국부 중심을 향하는 하나의 단위 벡터 n을 가지고 있다. 곡률의 중심은 커브 '내측'에서 발견되며, 그 모양에 따라 궤적의 양쪽으로 이동할 수 있다. 소포 위치와 곡률 중심 사이의 거리는 해당 위치에서 곡률 R의 반지름이다. 곡률 반경은 궤적이 곧게 되고 n의 포지티브 방향이 이 특별한 경우(지극성 흐름에서 논의)에 결정되지 않는 지점에서 무한 길이에 접근한다. 기준 프레임(s,n)은 그림의 빨간색 화살표로 표시된다. 이 틀은 축이 움직이는 소포에 지속적으로 조정되기 때문에 자연적 또는 내재적이라 불리며, 그 운명과 가장 밀접하게 연결되어 있다.
운동학
속도 벡터(V)는 s와 같이 방향을 잡고 강도(속도) V = ds/dt를 가진다. 이 속도는 소포가 자체 궤적을 따라 이동하기 때문에 항상 양수량이며, 증가 시간(dt>0)에는 트로이 목마 길이도 증가한다(ds >0).
소포의 가속 벡터는 s에 평행한 접선 가속도와 양의 n을 따라 구심 가속도에서 분해된다. 접선 가속은 속도 V만 변경하고 DV/Dt와 동일하며, 여기서 큰 d는 재료 파생물을 나타낸다. 구심 가속도는 항상 곡률 O의 중심을 가리키며, 소포가 이동하는 동안 전방 변위의 방향만 변경한다.
폭력
균형 흐름 이상화에서 우리는 다음과 같은 세 방향 힘의 균형을 고려한다.
- 압력력. 이것은 주변 기압 p의 공간적 차이에 의해 발생하는 소포에 대한 작용이다. (이곳에서는 일시적인 변화는 관심이 없다.) 압력의 공간적 변화는 등고선인 이소바를 통해 가시화된다. 등고선은 압력이 동일한 값을 갖는 위치에 결합한다. 그림에서 이것은 균일한 간격의 직선으로 단순하게 나타난다. 소포에 작용하는 압력력은 그림에서 파란색 화살표로 그려진 p의 구배 벡터를 뺀 값(기호: grad p)이다. 모든 점에서 압력 구배는 p의 최대 증가 방향을 가리키며 그 지점의 isobar에게는 항상 정상이다. 흐름 패킷이 높은 압력에서 낮은 압력까지 밀리는 것을 느끼기 때문에, 효과적인 압력 벡터 힘은 압력 구배와 반대로, 구배 벡터 앞에 마이너스 부호를 나타낸다.
- 마찰. 이것은 항상 전방 운동을 반대하며, 벡터는 반드시 음의 방향으로 작용하며 속도를 감소시킨다. 균형유동 모델에서 작용하는 마찰은 상공에서 지구 표면의 거칠기가 위쪽으로 더 높게 움직이면서 발휘되는 마찰이다. 단순성을 위해 여기서는 마찰력(단위 질량당)이 일정한 마찰계수 K를 통해 소포의 속도에 비례하여 조정된다고 가정한다. 보다 현실적인 조건에서는 느린 층류 흐름을 제외하고는 속도에 대한 마찰의존도가 비선형이다.
- 코리올리스 힘. 이 작용은 지구의 자전 때문에 북반구(남반구)에서 우측(왼쪽)으로 이동하는 모든 몸을 대체하는 경향이 있다. 단위 질량당 강도는 속도 V에 비례하며, 국부 코리올리스 주파수 f(적도의 북쪽과 음의 남쪽의 양수)에 비례하여 극성을 향해 적도(영점)에서 진도 증가한다. 따라서 코리올리스 벡터는 반드시 옆을 가리키며, 그것은 n축을 따라 있다. 코리올리 벡터는 지구 상에서 패킷의 위치에 기초하여 어느 한 쪽을 가리키는 반면, 곡률만을 기반으로 한 궤적의 오른쪽과 왼쪽 사이에 nf의 양적인 방향은 흐르기 때문에 균형 방정식에서 그것의 부호는 바뀔 수 있다. 코리올리 힘의 정확한 표현은 코리올리 파라미터와 소포의 속도보다 조금 더 복잡하다. 그러나 이 근사치는 지구 표면의 곡률을 무시한 것과 일치한다.
그림에서 그려지는 가공적인 상황에서, 압력력은 소포를 곡선을 따라 앞으로 밀고 안으로 굽힘에 대하여 밀어 넣으며, 코리올리 힘은 북반구(남반구)의 굽힘의 안쪽으로 (밖으로) 밀어 넣으며, 마찰은 뒤쪽으로 (필요하게) 당겨진다.
지배 방정식
소포의 동적 평형에서, 소포의 질량 시간 중 어느 한 요소는 동일한 방향으로 작용하는 외부 힘의 구성 요소와 동일하다. 소포의 평형 방정식은 자연 좌표로 작성되므로 단위 질량 당 수평 운동량에 대한 성분 방정식은 다음과 같이 표현된다.
=- p ± pressstyle {\ {\ nfV
③전방 방향과 측방 방향 각각, 여기서 ③은 공기의 밀도다.
용어는 다음과 같이 나눌 수 있다.
- / t {DV은(는) 소포에 대한 속도 변화의 임시 속도(접선 가속도)이다.
- - / 는 궤적을 따라 단위 부피 당 압력력의 구성 요소임.
- 은(는) 마찰로 인한 감속이다.
- / 은(는) 구심 가속이다.
- - / n은(는) 궤적에 수직인 단위 부피 당 압력력의 구성 요소임.
- 은 단위 질량당 코리올리 힘(징후 모호성은 힘 벡터와 n의 상호 방향에 따라 다름)이다.
정상 상태 가정
다음 논의에서 우리는 정상 상태의 흐름을 고려한다. 따라서 속도는 시간에 따라 변할 수 없으며 접선 가속을 생성하는 구성 요소 힘은 0까지 합해야 한다. 즉, D t = 0 을(를) 위해서는 능동력과 저항력이 전방 방향으로 균형을 이루어야 한다 중요한 것은, 거기에서 우측 힘이 유의하거나 무시할 수 있는 크기인지에 대해서는 아직 추정이 이루어지지 않고 있다. 더욱이 궤적과 흐름은 일정한 상태 조건에서 일치하며, 접선/정규형과 스트림/크로스스트림 형용사의 쌍은 서로 교환할 수 있게 된다. 접선 가속도가 무시할 수 없는 대기 흐름을 알리소바르식이라고 한다.
속도 방향은 관성 흐름을 제외하고 압력 패턴에 의해 설정된 궤적을 따라 여전히 공간 내에서 변할 수 있다.
일반 프레임워크
그 도식들은
접선 및 정규 균형 방정식에서 특정 용어를 제외하고, 우리는 다음과 같은 5개의 이상적인 흐름 중 하나를 얻는다: 반정립적 흐름, 측위적 흐름, 사이클로스트루시브 흐름, 관성 흐름, 그리고 구배 흐름. 나머지 용어들의 균형을 추론함으로써 우리는 이해할 수 있다.
- 압력장의 배열이 그러한 흐름을 지원하는 것.
- 항공기의 소포가 이동하는 궤적을 따라
- 어느 정도 속도라면 그렇게 할 수 있다.
다음 예/아니요 표는 각 이상화에서 어떤 기여를 고려하는지 보여준다. 에크만 층의 도식화 역시 완전성을 위해 언급되며, 공기와 지면 사이의 도식화보다는 공기의 내부 마찰이 수반되기 때문에 별도로 취급한다.
| 반정형 흐름 | 지압류 | 사이클로스트루시스 흐름 | 관성 흐름 | 그라데이션 흐름 | 에크만 흐름 | |
|---|---|---|---|---|---|---|
| 곡면성 | N | N | Y | Y | Y | N |
| 마찰의 | Y | N | N | N | N | Y |
| 압력을 가하다 | Y | Y | Y | N | Y | Y |
| 코리올리 | N | Y | N | Y | Y | Y |
제한 사항
공기 특성의 수직적 차이
이 방정식은 수평면에서 이동하는 공기의 소포에 적용된다고 한다. 실제로 대기열을 고려할 때 온도 및 수분 함량, 즉 밀도는 높이에 따라 변화하기 때문에 공기 밀도가 상승 높이와 동일한 경우는 드물다. 그러한 기둥 안에 있는 모든 소포는 그 자체의 높이에 있는 공기 특성에 따라 움직인다.
균일한 공기 층이 다른 층 위로 미끄러질 수 있으므로, 무거운 공기 위에 있는 가벼운 공기의 안정적인 층화가 잘 분리된 층으로 이어지는 한. 그러나 어떤 공기가 주변 공기보다 무겁거나 더 작다면 수직 운동이 일어나 수평 운동을 차례대로 수정한다. 자연에서 다운드래프트와 업드래프트는 때때로 지면에 평행한 움직임보다 더 빠르고 강렬할 수 있다. 균형 흐름 방정식은 침몰/부유 작용을 나타내는 힘 또는 속도의 수직 성분을 포함하지 않는다.
또한 압력이 일반적으로 지면/해면 수준 근처의 기기(기압계)를 통해 알려져 있다는 점도 고려하십시오. 보통 날씨 차트의 Isobar는 표시의 균일성을 위해 평균 해수면으로 조정된 이러한 압력 측정을 특정 시간에 요약한다. 이러한 값은 공기의 특정 중량 오버헤드 변경에 대한 세부 사항을 표시하지 않고 공기 기둥 오버헤드의 무게를 나타낸다. 또한 베르누이의 정리에 의해 측정된 압력은 공기의 상당한 수직 운동이 일어난다면 정확히 공기 기둥의 무게가 아니다. 따라서 높이가 다른 개별 공기 구획에 작용하는 압력력은 측정값을 통해 실제로 알려져 있지 않다. 표면 압력 차트에서 얻은 정보를 균형 흐름 제형으로 사용할 때, 힘은 전체 공기 기둥에 적용되는 것으로 가장 잘 보인다.
그러나 모든 공기 기둥의 공기 속도의 한 가지 차이는 변함없이 땅/바다 근처에서 발생한다. 또한 공기 밀도가 어디에서나 동일하고 수직 운동이 발생하지 않는 경우에도 발생한다. 거기서 접촉면의 거칠기는 위의 공기 운동을 느리게 하고, 이 지각 효과는 높이와 함께 서서히 사라진다. 예를 들어 행성 경계층을 참조하십시오. 마찰 반정형 흐름은 지면 근처에서 적용되는 반면, 다른 도식들은 지면에서 충분히 멀리 떨어져서 그것의 "브레이킹" 효과(자유 공기 흐름)를 느끼지 못할 정도로 적용된다. 두 집단을 개념적으로 분리해야 하는 이유다. 저유량에서 고유량 도식으로의 전환은 공대공 마찰, 코리올리, 압력력이 균형을 이루고 있는 에크만과 같은 도식으로 연결된다.
요약하면, 균형유속 속도는 균질(정수밀도, 수직운동 없음) 또는 기껏해야 안정적 층화(비정수밀도, 수직운동 없음)로 간주될 수 있는 공기열에 잘 적용된다. 만약 우리가 이러한 조건들이 발생하는지 확인할 수 없다면 추정치의 불확실성은 발생한다. 또한 마찰력의 온오프 처리로 인해 지구와의 접촉 표면에서 외부 대기까지 전체 기둥의 움직임을 설명할 수 없다.
공기 특성의 수평적 차이
공기 기둥이 높이와 균일하더라도 각 기둥이 위치별로 밀도가 변할 수 있는데, 첫째, 기단이 기원에 따라 온도와 수분 함량이 다르기 때문이다. 그 다음 기단이 지구 표면 위를 흐를 때 그 특성을 수정하기 때문이다. 예를 들어, 열대외 사이클론에서 낮은 압력 주위로 순환하는 공기는 일반적으로 차가운 공기 내에 온열온도의 섹터가 결합되어 있다. 사이클론 순환의 구배-흐름 모델은 이러한 특징을 허용하지 않는다.
균형 흐름 도식은 지구 표면의 위도 몇 도에 걸친 공기 흐름의 풍속을 추정하는 데 사용될 수 있다. 그러나 이 경우 일정한 코리올리스 파라미터를 가정하는 것은 비현실적이며, 균형유속은 국지적으로 적용할 수 있다. 위도 변화가 동적으로 효과적인 경우의 예로서 로스비 파장을 참조한다.
불안정성
균형유동 접근방식은 균형유동 압력패턴에서 도출된 대표적인 궤적과 정상상태 풍속을 파악한다. 실제로 기체의 축적(또는 밀도 증가)은 지상의 압력을 증가시키고, 그 반대로 기체의 운동과 압력 패턴은 서로 연결되어 있다. 어떤 새로운 압력 구배도 새로운 공기의 변위를 야기할 것이고, 따라서 연속적인 재배치를 야기할 것이다. 날씨 자체가 보여주듯이, 정상 상태의 상태는 예외적이다.
마찰력, 압력구배력, 코리올리스 힘이 반드시 균형을 이루는 것은 아니기 때문에 공기 질량은 실제로 가속하고 감속하기 때문에 실제 속도도 과거의 가치에 따라 달라진다. 다음에 보듯이 압력장과 유량 궤적을 평행이든 직각이든 간에 균형 잡힌 흐름으로 깔끔하게 배열하는 것은 꾸준한 유량을 가정하는 데서 비롯된다.
정상 상태 균형 유동 방정식은 애초에 흐름이 어떻게 동작하도록 설정되었는지 설명하지 않는다. 또한 압력 패턴이 충분히 빠르게 변화한다면, 균형 잡힌 흐름 속도는 단지 소포가 이동되는 동안 소포가 느끼는 힘이 변했다는 이유만으로 장거리 비행 구획을 추적할 수 없다. 이 입자는 원래 압력 패턴을 따랐던 경우와 비교해서 다른 곳으로 귀결될 것이다.
요약하면, 균형유동 방정식은 일정한 순간과 일정한 장소에서 상황을 추정할 수 있는 일관된 정상상태 풍속을 제공한다. 이러한 속도는 장기적으로 공기가 어디로 이동하는지 이해하기 위해 자신 있게 사용할 수 없다. 왜냐하면 강제력은 자연스럽게 변화하거나 압력 패턴에 대해 궤적이 왜곡되기 때문이다.
반정형 흐름
반정형 흐름은 다음과 같은 경우 공간적으로 변화하는 압력장 내에서 정상 상태 흐름을 설명한다.
- 전체 압력 구배는 마찰만으로 정확하게 균형을 맞춘다.
- 곡면성을 촉진하는 모든 조치는 무시된다.
이 이름은 그리스어 '안티'(반대, 반대)와 '트리프타인'(비비는 쪽)에서 유래했는데, 이는 이러한 흐름이 마찰에 대항하여 진행됨을 의미한다.
공식화
스트림 와이즈 모멘텀 방정식에서 마찰은 무시할 수 없는 압력 그라데이션 요소(K≠0)의 균형을 유지한다. 압력 그라데이션 벡터는 궤적 접선 s를 따라 구성 요소에 의해서만 만들어진다. 스트림와이즈 방향의 균형은 다음과 같이 정반대 속도를 결정한다.
긍정적인 속도는 사실이 너무 수학적으로 p/∂의<>∂이antitriptic이 흐르는 압력장의 아래쪽 비탈을,;0{\displaystyle{\partial p}{s\partial}<. 0}일 경우 이주간다면 보장되는 제품형 운동 에너지 탄두와ρ 일정은 그대로, 선형 s에 따라 달라지고 시간이 바꿔 궤도는 그러한 것이다.parce나는 같은 거리를 커버하는 동안 동등한 압력이 떨어지는 것을 느낀다. (이것은 물론, 다른 표면 거칠기를 허용하기 위해 공간에서 변화하는 마찰의 비선형 모델이나 마찰 계수를 사용할 때 변화한다.)
크로스스트림 운동 방정식에서 코리올리 힘과 정상 압력 구배가 모두 무시할 수 있어 순 굴절 작용이 없다. 원심용어 / 는 속도가 0이 아닌 상태에서 사라지므로 곡률 반경은 무한대로 가고 궤적은 직선이어야 한다. 또한 / = 0 이후 궤적은 이소바에 수직이다 n 방향이 이소바르의 방향일 때 s가 이소바에 수직이다. 따라서, 반정형 이소바는 등분 원 또는 직선이 되어야 한다.
적용
조건이 상당히 엄격하기 때문에, 반정형 흐름은 아마도 5개의 균형 흐름 이상화 중에서 가장 적게 이용될 것이다. 그러나 그 밑의 마찰이 일차적인 기여로 간주되는 유일한 것이다. 따라서, 반독점 도식은 지구 표면 근처에서 일어나는 흐름, 즉 일정 스트레스 층으로 알려진 지역에 적용된다.
사실, 상수압 층의 흐름은 종종 더 빠른 흐름 오버헤드에 의해 구동되기 때문에 이소바와 평행한 구성 요소를 가지고 있다. 이는 이소바와 평행하는 경향이 있는 높은 따옴표에서의 이른바 자유공기 흐름과 중간 따옴표에서의 에크만 흐름 때문에 발생하며, 이로 인해 자유공기 속도가 감소하고 표면에 접근하는 동안 방향이 전환된다.
코리올리 효과는 무시되기 때문에 정전기류와는 반대로, 에크만 흐름의 숫자가 클 때마다 적도 부근이나 그 밖의 다른 곳(운동의 길이 척도와 무관하게), 또는 (보통 소규모 공정의 경우) 정전기류 흐름이 발생한다.
대초원의 바닷바람, 에크만 펌프질, 저준위 제트기와 같은 일부 경계층 현상을 설명하는 데 반정형 흐름을 사용할 수 있다.[1]
지압류
지리적 흐름은 공간적으로 변화하는 압력장 내에서 일정한 상태의 흐름을 말한다.
- 마찰 효과는 무시된다. 그리고:
- 전체 압력 구배는 정확하게 코리올리 힘만 균형 잡는다(곡률 없이 결과).
'지극성'이라는 이름은 그리스어 'ge'(지구)와 'strepein'(회전하기 위해)에서 유래한다. 이 어원은 궤도의 회전을 암시하는 것이 아니라 지구 주위를 도는 것을 암시한다.
공식화
스트림과 같은 운동 방정식에서, 무시해도 될 마찰은 K=0으로 표현되며, 정상 상태 균형을 위해 무시할 수 있는 스트림과 같은 압력력이 따른다.
이 균형으로는 속도를 알 수 없다. 그러나 / = 0 에는 궤적이 이소바를 따라 흐르지 않으면 이동 소포에 대한 압력의 변화가 발생한다. 따라서 이소바가 첫 번째 경우 직선일 때만 벤딩이 가능하지 않다. 그래서 지리적 흐름은 그러한 이소바를 따라 흐르는 시냇물의 모습을 취한다.
교차 스트림 운동 방정식에서 비굴착 코리올리 힘은 소포가 어떠한 굽힘 작용도 경험하지 않는 방식으로 압력력에 의해 균형을 이룬다. 궤적이 구부러지지 않기 때문에, 곡률 중심 부재로 n의 포지티브 방향을 결정할 수 없다. 이 경우 정상 벡터 성분의 기호는 불확실해진다. 그러나 어쨌든 기압력은 코리올리 힘의 균형을 정확히 맞춰야 하기 때문에 기압의 측면 경사도가 줄어드는 것과는 반대로 기압의 소포는 코리올리 힘과 함께 이동해야 한다. 따라서 단위 벡터 n을 공식적으로 설정하는 불확실성과 관계없이 소포는 항상 북반구(남반구)에서 왼쪽(우측)에 낮은 압력으로 이동한다.
정지신속도는
= 1 {\{1.
정지궤도 속도의 표현은 정반대 속도의 표현과 유사하다. 여기서 속도는 이소바르를 따라 발달하는 궤적을 가로지르는 압력 경사의 크기에 의해 결정된다.
적용
모델러, 이론가 및 운영 예측자는 지리적/지리적 근사치를 자주 사용한다. 마찰은 중요하지 않기 때문에, 지구 표면 위로 충분히 높이 흐른다. 코리올리 힘은 관련성이 있기 때문에 일반적으로 로스비 수가 적은 공정에 적합하며, 일반적으로 길이 눈금이 크다. 정전기적 조건 또한 정전기적 조건과 반대로 Ekman 수가 적은 흐름의 경우 실현된다.
잘 정의된 한 쌍의 고압과 저압 사이에서 지압 조건이 발달하거나, 주요 지압류가 그 양쪽에 있는 몇 개의 고압과 저압으로 옆을 이루는 경우가 빈번하다(이미지 참조). 균형유량방정식은 내부(공대공) 마찰이 허용되지 않지만, 지반하천과 인근 회전계통의 흐름 방향도 이들 사이의 전단 접촉과 일치한다.
지압류 흐름의 속도는 같은 압력 구배를 가진 낮은 압력(높음) 주위의 곡선 흐름에서보다 더 크다(작다). 이 특성은 보다 일반적인 구배류 도식으로 설명된다. 이는 보다 복잡한 배열의 역추정으로서 지리적 근위축 속도를 사용하는 데 도움이 된다. 아래 비교한 균형 잡힌 흐름 속도도 참조한다.
표시된 어원과 압력 차트는 반드시 그렇지는 않지만, 지리적 흐름이 다소 큰 스케일로 대기 운동을 설명할 수 있음을 시사한다.
사이클로스트루시스 흐름
사이클로스트루시브 흐름은 다음과 같은 경우에 공간적으로 변화하는 압력장에서 정상 상태 흐름을 나타낸다.
- 마찰 및 코리올리 작용은 무시된다.
- 구심 가속도는 압력 경사로 인해 완전히 유지된다.
궤도는 구부러진다. '사이클로스트로시브'라는 이름은 그리스어 '키클로스'(순환)와 '스트레페인'(회전하기 위해)에서 유래했다.
공식화
지압 균형에서와 마찬가지로 흐름은 마찰이 없고, 정상 상태의 움직임을 위해 궤도는 이소바를 따른다.
크로스스트림 운동 방정식에서는 코리올리스 힘만 버려 구심 가속도는 단위 질량 당 크로스스트림 압력 힘일 뿐이다.
=- p frac {\
이는 궤적이 굽힘 작용의 대상이 되며, 사이클로스트루시스 속도는 휨 작용의 대상이 된다는 것을 의미한다.
=- p {\V={\{R}{\{\ p
그래서 사이클로스트루시스 속도는 궤적을 가로지르는 압력 경사의 크기와 이소바르의 곡률 반경에 의해 결정된다. 그 흐름은 더 빠르며, 비록 선형은 아니지만 곡률 중심에서 더 멀리 떨어져 있다.
크로스스트림 운동 방정식의 또 다른 함축적 의미는 사이클로스트루시브 흐름이 저압 영역 옆에서만 발달할 수 있다는 것이다. 이는 제곱근 아래의 수량이 양수라는 요건에 함축되어 있다. 사이클로스트루시스 궤적이 이소바르인 것으로 밝혀졌음을 상기하라. 압력이 곡률 중심에서 바깥쪽으로 상승하고, 압력 유도체가 음이고, 제곱근을 잘 정의할 경우에만 곡률 중심 압력이 낮아야 한다. 위의 수학은 사이클로스트루시스 회전이 시계방향으로 끝나는지 반시계방향으로 끝나는지의 실마리를 주지 못하는데, 이는 결국 배열이 관계에서 허용되지 않는 효과의 결과, 즉 모세포 회전이 된다는 것을 의미한다.
적용
사이클로스트로이드 도식화는 코리올리와 마찰력이 둘 다 무시할 수 있을 때, 즉 로스비 숫자와 작은 에크만 숫자를 가진 흐름을 위한 것이다. 코리올리 효과는 보통 낮은 위도나 작은 규모에서 무시해도 좋다. 토네이도, 더스트 데블, 워터프루프 같은 시스템에서는 사이클로스트로이드 균형이 달성될 수 있다. 사이클로스트루시스 속도도 다음에 나타낸 것처럼 구배 균형 속도의 기여 중 하나로 볼 수 있다.
사이클로스트로이드 도식을 이용한 연구들 중 레노와 블루스타인은 사이클로스트로이드 속도 방정식을 사용하여 물웅덩이에 대한 이론을 수립하고 윈, 후냐디, 울리치는 사이클로스트로이드 근사치를 사용하여 1995년 6월 8일 텍사스주 앨리슨 근처에서 지나간 대형 토네이도의 최대 접선 바람을 계산한다.
관성 흐름
다른 모든 흐름과 달리 관성 균형은 균일한 압력장을 의미한다. 이러한 이상화에서:
- 흐름이 무마찰이다.
- 압력 구배(및 힘)가 전혀 존재하지 않는다.
유일하게 남은 작용은 궤도에 곡률을 전해주는 코리올리 힘이다.
공식화
전과 같이 정상 상태 조건에서의 무마찰 흐름은 ∂ / = 을 의미하지만, 이 경우 이소바는 애초에 정의되지 않는다 우리는 압력장의 배열로부터 궤적에 대한 어떠한 기대도 이끌어 낼 수 없다.
크로스 스트림 운동 방정식에서 압력력을 생략한 후 구심 가속도는 단위 질량 당 코리올리 힘이다. 휨은 오로지 곡률의 측면을 도전하지 않고 설정하는 코리올리 힘에 의해 결정되기 때문에 부호 모호성은 사라진다. 따라서 이 힘은 항상 긍정적인 부호를 가진다. 관성 회전은 북반구(남반구)에서 시계방향(반시계방향)으로 한다. 모멘텀 방정식
= {V
우리에게 관성 속도를 준다.
= R
관성 속도의 방정식은 한 번 다른 것이 주어지면 속도나 곡률 반경을 결정하는 데 도움이 된다. 이 움직임에서 비롯된 궤적을 관성 원이라고도 한다. 균형 흐름 모델은 일부 외부 섭동에 의해 촉발되어야 하는 관성 원의 초기 속도에 대한 단서를 제공하지 않는다.
적용
대기 운동은 주로 압력 차이에 기인하기 때문에 관성 흐름은 대기 역학에서 그리 적용할 수 없다. 그러나 관성 속도는 구배 속도의 해법에 기여하는 것으로 나타난다(다음 참조). 더욱이 관성 흐름은 높은 밀도로 인해 공기보다 압력 차이에 의해 움직이는 흐름이 적은 해양 흐름에서 관찰된다. 즉, 표면 바람에 의해 전달되는 마찰이 아래로 사라지도록 깊숙한 곳에서 내부 균형이 발생할 수 있다.
그라데이션 흐름
구배 흐름은 곡률도 고려하기 때문에 지반성 흐름의 연장선으로, 이는 상층 대기의 흐름에 대한 보다 정확한 근사치가 된다. 그러나 수학적으로 구배 흐름은 약간 더 복잡하고, 지리적 흐름은 상당히 정확할 수 있기 때문에 구배 근사치가 자주 언급되지는 않는다.
그라데이션 흐름은 또한 사이클로스트루시브 밸런스의 연장선이기도 한데, 코리올리 힘의 효과를 가능케 하기 때문에 로스비 번호로 어떤 흐름에도 적합하다.
마지막으로, 관성 균형의 확장인데, 그것은 흐름을 움직이는 압력력을 허용하기 때문이다.
공식화
반정형 균형을 제외한 모든 것과 마찬가지로 흐름의 운동 방정식에서 마찰력과 압력력은 무시되므로, 흐름이 이소바와 평행하다는 것은 / = 0 p로부터 따르게 된다.
V 수율에 대한 2차 방정식으로 전체 교차 스트림 모멘텀 방정식 해결
.
구배 풍속의 모든 해결책이 물리적으로 타당한 결과를 산출하는 것은 아니다. 즉, 우측 전체는 속도의 정의 때문에 양수여야 하며, 제곱근 아래의 양은 음수여야 한다. 첫 번째 부호 모호성은 코리올리 힘과 단위 벡터 n의 상호 방향에서 오는 반면, 두 번째 부호는 제곱근에서 오는 것이다.
싸이클론적 순환과 반사이클로닉적 순환의 중요한 경우들은 다음에 논의된다.
압력 낮음 및 사이클론
일반 사이클론(압력저하 주위의 공기 순환)의 경우, 기압력은 반구와 무관하게 내부(양수기), 코리올리 힘은 외부(음수기)이다. 교차 대상 운동 방정식은 다음과 같다.
= - { n - f }{\ p}\ {\partial p}{\p}\partial n
양쪽을 f V로 나누면, 라는 것을 인식하게 된다.
,
여기서 사이클론 구배 속도 V는 해당 측위성 및 정확도가 낮은 추정치보다 작으며 곡률 반경이 증가함에 따라 자연스럽게 접근한다(관성 속도가 무한대로 이동함에 따라). 그러므로 사이클론에서는 곡률로 인해 정지궤도 속도의 무곡선 값에 비해 흐름이 느려진다. 아래 비교한 균형 흐름 속도도 참조하십시오.
사이클론 방정식의 양근은
.
이 속도는 제곱근 아래의 양이 항상 양이기 때문에 항상 잘 정의된다.
압력 최고치 및 부동액
앤티시클론(압력높이 주변의 공기 순환)에서 코리올리 힘은 항상 안쪽으로(그리고 양성으로), 압력력은 반구와 관계없이 바깥쪽으로(그리고 음으로) 나간다. 교차 대상 운동 방정식은 다음과 같다.
=- p + f fracp}}{\ F
양쪽을 f V로 나누면, 우리는 얻는다.
,
여기서 반냉동 구배 속도 V는 정지영역 값보다 크며 곡률 반경이 커질 때 접근한다. 따라서 안티사이클론에서는 (기후성) 무커버 값에 비해 이소바 곡률로 인해 공기 흐름이 빨라진다. 아래 비교한 균형 흐름 속도도 참조하십시오.
V에는 두 가지 양의 뿌리가 있지만, 지구온난화의 한계와 일치하는 유일한 뿌리는
이 al 2 c o y c l t p i{\는 의미가 있어야 한다. 이 조건은 특정 위도에서 일정한 압력 기울기를 갖는 고압 구역을 감안할 때 바람이 없는 고도를 중심으로 원형 지역이 있어야 한다는 요건에서 해석할 수 있다. 그 둘레에서 공기는 해당 관성 속도의 절반(사이클론스트루시브 속도로)으로 불고, 반경은 다음과 같다.
= R{\{\ p n
R에 대한 위의 불평등을 해결함으로써 얻어진다. 이 원을 벗어나면 곡률 반경이 증가함에 따라 속도가 정지영역 값으로 감소한다. 이 반지름의 폭은 압력 경사의 강도에 따라 증가한다.
적용
Gradient Flow는 Rossby 숫자가 작은 고압 및 저압 중심 주위를 회전하는 대기 흐름을 연구하는데 유용하다. 이것은 압력 중심부 주위의 흐름의 곡률 반경이 작고, 유용한 정도의 정확도를 가지고 더 이상 지리적 흐름이 적용되지 않는 경우다.
균형 흐름 속도 비교
각 균형 흐름 이상화는 동일한 조건에서 풍속에 대해 다른 추정치를 제공한다. 여기서 우리는 대기권 상층부에서 유효한 도식에 초점을 맞춘다.
첫째로, 해면 500미터 상공에서 샘플 공기 소포가 흐르므로 마찰 효과는 이미 무시할 수 있다고 상상해보자. 평균 해발 500m 상공의 (건조) 공기의 밀도는 상태 방정식에 따라 1.167kg/m이다3.
둘째, 유량을 구동하는 압력력을 1hPa/100km(평균값)의 변화율로 측정하도록 한다. 그것이 중요한 것은 압력의 가치가 아니라 그것이 궤도에 걸쳐 변화하는 경사라는 것을 상기하라. 이 경사는 직선 이소바(지반성 유량) 또는 곡선 이소바(지반성 유량 및 구배 유량)의 간격에도 동일하게 잘 적용된다.
셋째, 소포를 남반구나 북반구 중 어느 쪽이든 위도 45도의 위도로 이동시켜 코리올리 힘은 코리올리 매개변수 0.000115Hz로 작용한다.
균형 흐름 속도도 궤적/이소바의 곡률 반경 R에 따라 변화한다. 도식화된 사이클론이나 앤티시클론처럼 원형 이소바의 경우 곡률 반경도 각각 낮은 압력과 높은 압력으로부터의 거리가 된다.
100km와 300km의 거리 R 중 2개를 차지하면 속도는 (m/s 단위)
| 지오스트레시브 | 사이클로스트루시브 | 관성체 | 구배(H-압력) | 구배(L-압력) | |
|---|---|---|---|---|---|
| R=100km | 7.45 | 9.25 | 11.50 | 해당 없음 | 5.15 |
| R=300km | 7.45 | 16.00 | 34.50 | 10.90 | 6.30 |
이 차트는 위에서 선택한 조건과 곡률 반경이 증가하면서 서로 다른 속도가 어떻게 변화하는지 보여준다.
정지신속(핑크라인)은 곡률에 전혀 의존하지 않고 수평선으로 나타난다. 그러나 곡률 반경이 무한히 커짐에 따라 사이클론 및 반발성 경사도 속도에 접근한다. 즉, 지반성 균형은 실제로 소멸하는 구심 가속(즉, 압력과 코리올리스 힘이 정확히 균형을 유지하는 경우)에 대한 구심 흐름의 제한적인 경우다.
사이클로스트루시브 속도(검은색 선)는 0에서 증가하며, R에 따른 성장률은 선형보다 낮다. 실제로 유량을 지탱하는 조건이 어느 정도 거리에서는 변화하기 때문에 무한의 속도 성장이 불가능하다. 또한 사이클로스트루시스 조건이 소규모 공정에 적용되므로 더 높은 방사선에 대한 외삽은 물리적으로 무의미하다는 것을 기억하라.
우리가 선택한 압력 구배와 무관한 관성 속도(녹색선)는 0에서 선형적으로 증가하며 곧 다른 어떤 것보다 훨씬 커진다.
구배 속도는 압력 낮음(파란색)과 압력 높음(빨간색) 주위의 속도에 유효한 두 개의 곡선과 함께 제공된다. 사이클론 순환에서의 풍속은 반경이 증가함에 따라 0에서 증가하며 항상 정지궤도 추정치보다 낮다.
냉동기 순환 예에서, 260 km (지점 R*)의 거리 내에 바람이 없다 – 이곳은 높은 압력 주변의 바람이 불지 않는/낮은 지역이다. 그 거리에서 첫 번째 반냉풍은 사이클로스트루시브 바람(점 Q)과 속도가 같고 관성 바람(점 P)의 절반이다. R* 지점에서 더 멀리 떨어진 곳에서, 반냉풍은 속도가 느려지고 속도가 감소할 정도로 큰 지리적 값에 접근한다.
또한 곡선에는 관성, 사이클로스트루시브 및 정지스트루시브 속도가 동일한 S로 표시된 또 다른 주목할 점이 있다. S의 반지름은 항상 R*의 4분의 1로 여기서 65km이다.
일부 도식화의 한계도 명백해진다. 예를 들어, 자오선을 따라 곡률 반경이 증가함에 따라, 해당 위도의 변화는 코리올리 매개변수의 다른 값과, 나아가 힘을 암시한다. 반대로 반경이 평행하면 코리올리 힘은 그대로 유지된다. 따라서, 원형의 흐름의 경우, 공기 소포는 다른 위도를 가로질러 이동할 때 코리올리 힘의 다른 강도를 느낄 것이기 때문에, 소포의 속도가 전체 원을 중심으로 시간적으로 변하지 않을 가능성이 낮다. 또한 압력장은 원주위를 모두 같은 간격을 유지하는 깔끔한 원형 이소바 형태를 취하는 경우는 거의 없다. 또한, 밀도의 중요한 차이는 수평 계획에서도 발생한다. 예를 들어, 따뜻한 공기가 사이클론 순환과 결합할 때, 따라서 한랭과 따뜻한 전선 사이에 따뜻한 구역을 형성한다.
참고 항목
참조
- ^ Schaefer Etling, J.; C. Doswell (1980). "The Theory and Practical Application of Antitriptic Balance". Monthly Weather Review. 108 (6): 746–756. Bibcode:1980MWRv..108..746S. doi:10.1175/1520-0493(1980)108<0746:TTAPAO>2.0.CO;2. ISSN 1520-0493.
- ^ Rennó, N.O.D.; H.B. Bluestein (2001). "A Simple Theory for Waterspouts". Journal of the Atmospheric Sciences. 58 (8): 927–932. Bibcode:2001JAtS...58..927R. doi:10.1175/1520-0469(2001)058<0927:ASTFW>2.0.CO;2. ISSN 1520-0469.
- ^ Winn, W.P.; S.J. Hunyady G.D. Aulich (1999). "Pressure at the ground in a large tornado". Journal of Geophysical Research. 104 (D18): 22, 067–22, 082. Bibcode:1999JGR...10422067W. doi:10.1029/1999JD900387.
추가 읽기
- 홀튼, 제임스 R: 2004년 동적 기상학 소개 ISBN 0-12-354015-1
외부 링크
- 미국기상학회 용어집
- NE Atlantic 및 Europe의 Met Office 영국 압력도
- 플리머스 주 기상센터 균형 잡힌 흐름 자습서 2007년 7월 8일 웨이백 기계에 보관



 궤적을 따라 단위 부피 당 압력력의 구성 요소임.
궤적을 따라 단위 부피 당 압력력의 구성 요소임. (는) 마찰로 인한 감속이다.
(는) 마찰로 인한 감속이다. (는) 구심 가속이다.
(는) 구심 가속이다. (는) 궤적에 수직인 단위 부피 당 압력력의 구성 요소임.
(는) 궤적에 수직인 단위 부피 당 압력력의 구성 요소임.

