점성성

점탄성은 고체의 속도에 의존하는 비탄성 행동을 설명하는 연속역학 이론이다. 이 맥락에서 비율 의존성은 재료의 변형이 하중을 가하는 속도에 따라 결정된다는 것을 의미한다.^[1] 점탄성의 주체인 비탄성 거동은 소성변형으로, 하중 수준에 도달했을 때 물질이 회복 불가능한 변형을 겪게 된다는 것을 의미한다. 일시적인 가소성 계산에는 요율 의존적 가소성이 중요하다. 비율에 독립적인 플라스틱 모델과 점성 물질 모델의 주요 차이점은 후자가 하중을 적용한 후 영구적인 변형을 보일 뿐만 아니라 가해진 하중의 영향을 받아 시간의 함수로서 계속 크리프 흐름을 겪는다는 것이다.

점성물질의 탄성반응은 후크 스프링 원소에 의해 일차원적으로 표현될 수 있다. 속도 의존성은 점탄성과 유사한 방식으로 비선형 대시팟 요소로 나타낼 수 있다. 가소성은 그림 1과 같이 슬라이딩 마찰 요소를 추가하여 설명할 수 있다.^[2] 그림 E는 탄성계수, λ은 점성계수, N은 비선형 대시팟[σ(dε/dt)= σ = λ(dε/dt)]^(1/N)을 나타내는 파워로법형 매개변수다. 슬라이딩 요소는 그림 1c와 같이 변형률에 의존하거나 심지어 일정한 항복 응력(수율_y)을 가질 수 있다.

점성성은 보통 Perzyna 또는 Dubaut-Lions 유형의 오버스트레스 모델을 사용하여 3차원 모델링.^[3] 이러한 모델에서 응력은 하중을 가할 때 요율 독립적인 항복 표면 이상으로 증가하도록 허용되었다가 시간이 지남에 따라 항복 표면으로 되돌아갈 수 있다. 수율 표면은 일반적으로 그러한 모델에서 요율에 의존하지 않는 것으로 가정된다. 대안적 접근방법은 수율 스트레스에 변형률 의존성을 추가하고 비율 독립적인 가소성 기법을 사용하여 재료의^[4] 반응을 계산하는 것이다.

금속과 합금의 경우, 점탄성은 곡물의 탈구 이동과 연계된 메커니즘에 의해 야기되는 거시적 행동이며, 결정간 활공(crystaline gliding)의 초점화 효과를 가진다. 이 메커니즘은 보통 절대 용해 온도의 약 1/3보다 큰 온도에서 지배적이 된다. 그러나 특정 합금은 상온(300K)에서 점성성을 나타낸다. 폴리머, 목재, 비투멘의 경우 탄력성이나 점탄성의 한계를 벗어난 행동을 기술하기 위해서는 점탄성 이론이 필요하다.

일반적으로 점성 이론은 다음과 같은 분야에서 유용하다.

• 영구 변형 계산,
• 구조물의 플라스틱 붕괴 예측,
• 안정성의 조사,
• 충돌 시뮬레이션,
• 엔진의 터빈과 같은 고온에 노출된 시스템(예: 발전소)
• 높은 변형률에 노출된 동적 문제 및 시스템

역사

가소성 이론에 대한 연구는 1864년 앙리 트레스카,^[5] 세인트 베넌트(1870), 레비(1871년)^[6]의 최대 전단 기준에 대한 연구로 시작되었다.^[7] 향상된 가소성 모델은 1913년 폰 미제스에^[8] 의해 제시되었는데, 현재 폰 미제스의 항복 기준으로 언급되고 있다. 본능적으로, 수학 모델의 개발은 안드레드의 법칙에 의한 1차 크리프의 표현과 함께 1910년으로 거슬러 올라간다.^[9] 1929년 노튼은^[10] 2차 크리프의 비율을 스트레스와 연계한 1차원 대시팟 모델을 개발했다. 1934년, 오드크비스트는^[11] 다축 케이스에 노턴의 법칙을 일반화했다.

수율표면에 대한 플라스틱 흐름의 정규성, 플라스틱성에 대한 흐름 규칙과 같은 개념은 프란틀(1924년)^[12]과 러스(1930년)에 의해 도입되었다.^[13] 1932년, 호헤넴서와 프라거는^[14] 느린 점성 흐름의 첫 번째 모델을 제안했다. 이 모델은 압축 불가능한 빙엄 고체에^[15] 대한 일탈 스트레스와 변형률 사이의 관계를 제공했다. 그러나 이러한 이론의 적용은 한계 이론이 발견된 1950년 이전에는 시작되지 않았다.

In 1960, the first IUTAM Symposium “Creep in Structures” organized by Hoff^[16] provided a major development in viscoplasticity with the works of Hoff, Rabotnov, Perzyna, Hult, and Lemaitre for the isotropic hardening laws, and those of Kratochvil, Malinini and Khadjinsky, Ponter and Leckie, and Chaboche for the kinematic hardening laws. 1963년 페르지나는 온도와 시간에 의존하는 점성 계수를 도입했다.^[17] 공식화된 모델은 되돌릴 수 없는 과정의 열역학 및 현상학적 관점에 의해 뒷받침되었다. 이 작품들에서 제시된 아이디어들은 요율 의존적 플라스틱성에 대한 대부분의 후속 연구의 기초가 되어 왔다.

현상학

정성적 분석을 위해 점성 물질의 현상학을 설명하기 위해 몇 가지 특성 시험을 수행한다. 이러한 테스트의 몇 가지 예는 다음과 같다.

1. 일정한 스트레스 또는 변형률의 강화 시험,
2. 일정한 힘으로 소름끼치는 시험과
3. 끊임없는 긴장의 스트레스 완화

변형경화시험

항복의 한 가지 결과는 플라스틱 변형이 진행됨에 따라 추가적인 변형을 생성하기 위해 응력의 증가가 요구된다는 것이다. 이러한 현상을 스트레인/작업 경화라고 한다.^[18] 점성 재료의 경우 강화 곡선은 비율에 독립적인 플라스틱 재료와 유의하게 다르지 않다. 그럼에도 불구하고 세 가지 본질적인 차이를 관찰할 수 있다.

1. 같은 변종에서 변형률이 높을수록 스트레스도 높아진다.
2. 시험 중 변형률의 변화는 응력-변형 곡선에 즉각적인 변화를 가져온다.
3. 플라스틱 수율 한도의 개념은 더 이상 엄격하게 적용할 수 없다.

탄성 부분과 플라스틱 부분을 분리하여 균주를 분할한다는 가설은 균주가 작은 곳에서도 여전히 적용된다.^[3]

${\displaystyle {\barembol {\barepsilon }={\mathrm {e}+{\mathsymbol {\vp}}}}}}}}{\mathrm {vp}}}}}}}}}$

$여기$서 $\epsilon {\displaystyle {\mathit{}}_{}}$ ${\$은 탄력성 변형이고 ${\displaystyle {\mathrm{}}_{}}$ v ${\displaystyle {\mathrm{p}}_{}}$ ${\$은 점성 변형이다. 그림에서 파란색으로 표시된 응력 변형률을 얻기 위해 재료는 처음에 0.1/s의 변형률로 적재된다. 그런 다음 변형률은 즉시 100/s로 상승하고 한동안 그 값으로 일정하게 유지된다. 이 기간이 끝나면 스트레인율은 0.1/s로 즉시 감소하고 스트레인 값을 증가시키기 위해 사이클을 계속한다. 변형률 변화와 스트레스 반응 사이에는 분명한 차이가 있다. 이 지연은 과압 모델(예: Perzyna 모델)에 의해 상당히 정확하게 모델링되지만, 요율 의존적인 항복 응력을 갖는 요율 독립적인 가소성 모델에는 모델링되지 않는다.

크리프 테스트

그림 3a. 크리프 테스트

그림 3b. 크리프 테스트에서 시간의 함수로서 스트레인.

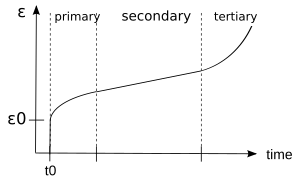
크리프는 고체 물질이 일정한 스트레스에 의해 영구적으로 천천히 움직이거나 변형되는 경향이다. 크리프 시험은 그림 3과 같이 일정한 스트레스로 인한 변형 반응을 측정한다. 고전적인 크리프 곡선은 일정한 온도에서 단축 응력을 받는 물질에서 시간의 함수로서 스트레인의 진화를 나타낸다. 예를 들어 크리프 시험은 일정한 힘/스트레스를 적용하고 시스템의 변형률 반응을 분석하여 수행한다. 일반적으로 이 곡선은 그림 3b에 나타난 바와 같이 보통 3상 또는 동작^[9] 기간을 나타낸다.

1. 과도 크리프라고도 알려진 1차 크리프 단계는 재료의 경화가 처음에는 매우 높은 흐름 속도의 감소로 이어지는 시작 단계다. ${\displaystyle (0}$ ${\displaystyle \le }$ ${\displaystyle \epsilon \mathit{}}$ ${\displaystyle \le }$ ${\displaystyle {\mathit{}}_{}}$ $1$ 1${\displaystyle {}_{}}$) ${\displaystyle (0\leq {\barembol {\barembol }}\barembol {\barembol$ $\}\}\}.$
2. 안정상태라고도 알려진 2차 크리프 단계는 변형률이 일정한 곳이다. ${\displaystyle ({\mathit{}}_{}}$ ${\displaystyle {}_{}}$≤ ${\displaystyle \epsilon \mathit{}}$ ${\displaystyle \le }$ 2 2 2 ${\displaystyle {\mathit{}}_{}}$ $2$2$$) {\$displaystyle ({\\boldsymbol {\\barepsilon }}{1}\\\boldsymbol {\\varepsilon$ $\}\}\}.$
3. 파단 변형률까지 변형률이 증가하는 3차 크리프 단계. ${\displaystyle ({\mathit{}}_{}}$ ${\displaystyle {}_{}}$≤ ${\displaystyle \epsilon \mathit{}}$ ${\displaystyle \le }$ ε$$ $r$ ${\displaystyle {}_{}}$ R$$) {\$displaystyle({\boldsymbol {\barebsylon }}{2}}\leq {\boldsymbol {\baldsylon$ $\}\}\}.$

이완시험

그림 4와 같이 이완시험은^[19] 일정기간 지속적인 스트레스로 인한 응력반응으로 정의된다. 점성 재료에서 이완 테스트는 일정한 변형률에서 단축하중의 응력 완화를 입증한다. 사실, 이러한 테스트는 점도의 특성을 나타내며 스트레스와 점성 변형률 사이에 존재하는 관계를 결정하는 데 사용될 수 있다. 변형률의 분해는

${\displaystyle {\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}}{\mathrm {d} t}}={\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {e} }}{\mathrm {d} t}}+{\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {vp} }}{\mathrm {d} t}}~.}$

변형률의 탄성 부분은 다음과 같다.

${\displaystyle {\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {e} }}{\mathrm {d} t}}={\mathsf {E}}^{-1}~{\cfrac {\mathrm {d} {\boldsymbol {\sigma }}}{\mathrm {d} t}}}$

변형 시간 곡선의 평평한 부분의 경우, 총 변형률은 0이다. 그래서 우리는,

${\displaystyle {\cfrac {\mathrm {d} {\boldsymbol {\varepsilon }}_{\mathrm {vp} }}{\mathrm {d} t}}=-{\mathsf {E}}^{-1}~{\cfrac {\mathrm {d} {\boldsymbol {\sigma }}}{\mathrm {d} t}}}$

따라서 이완 곡선을 사용하여 1차원 점성 재료 모델에서 점성 변형률과 대시팟의 점도를 결정할 수 있다. 이완 시험의 마지막에 스트레스가 고원되었을 때 도달하는 잔존값은 탄성 상한에 해당한다. 암염과 같은 일부 물질의 경우, 그러한 탄성 상한은 스트레스라는 매우 작은 값에서 발생하며 이완 테스트는 스트레스에서 관찰할 수 있는 고원 없이 1년 이상 지속할 수 있다.

이완 테스트는 시험에서$$ ${\displaystyle \frac{d\mathrm{}}{}}$ ${\displaystyle \frac{=}{}}$ d ${\displaystyle \frac{t}{}}$ = ${\displaystyle 0}$ ${\dplaystyle {\cfrac {\cfrac$ {$d}{\boldsymbol {\varepsilon }}}{\mathrm {d} t}=0}$ 상태를 유지하는 것은 상당한 섬세함이 필요하기 때문에 수행하기가 매우 어렵다는 점에 유의해야 한다.^[20]

점성성의 Rheological models of viscaplasticity.

스프링-대시팟-슬라이더 요소에 기초한 점성성을 위한 1차원 구성 모델에는 완벽한 점성 고형, 탄성 완벽한 점성 고형, 탄성 완전 점성 경화 고형이 포함된다^[3]. 원소는 직렬 또는 병렬로 연결할 수 있다. 요소들이 직렬로 연결된 모델에서 스트레스는 각 요소에서 동일한 반면 스트레스는 첨가된다. 병렬 연결에서 응력은 가법적인 반면 스트레인은 각 원소에서 동일하다. 이러한 1차원 모델들 중 다수는 작은 변형률 체계에 대해 3차원까지 일반화할 수 있다. 이후 논의에서 시간률의 변형률과 스트레스는 각각 $\$ {\$displaystyle {\dot {\boldsymbol {\varepsilon }}},$ ${\displaystyle \stackrel{}{\{}}${\$dot {\dot$ {\$boldsymbol$ {\$sigma$로 기재된다.

완벽한 점성 고체(Norton-Hoff 모델)

점성성의 노턴-호프 모델이라고도 불리는 완벽하게 점성 고체에서 응력(점성 유체에 대한 경우)은 영구 변형률의 함수다. 탄성 효과는 ${\displaystyle \mathrm{모델}}$에서 무시되며, 즉$$ $\epsilon {\displaystyle {\mathit{}}_{}}$ ${\displaystyle e_{}}$${\displaystyle {}_{}}$= 0 ${\displaystyle {\boldsymbol {\$boldsymbol {\$valdsymbol$ $}}_{e}=0})$ $따라서{\displaystyle {}_{}}$ 초기 항복 응력은 없다$.$ 점성 대시보드의 응답은

${\displaystyle {\boldsymbol {\sigma }}=\eta ~{\dot {\boldsymbol {\varepsilon }}}_{\mathrm {vp} }\implies {\dot {\boldsymbol {\varepsilon }}}_{\mathrm {vp} }={\cfrac {\boldsymbol {\sigma }}{\eta }}}$

여기서 $\eta {\displaystyle }$ ${\displaystyle \eta }$은(는) 대시 포트의 점성이다. Norton-Hoff 모델에서 점성 $\eta {\displaystyle }$ ${\displaystyle \eta }$은(는) 적용된 응력의 비선형 함수로서$$ 다음과 같이 주어진다.

${\displaystyle \eta =\lambda \left[{\cfrac {\lambda }{{\boldsymbol{}}}}}}}{{N-1}$

where ${\displaystyle N}$ is a fitting parameter, λ is the kinematic viscosity of the material and ${\displaystyle {\boldsymbol {\sigma }} ={\sqrt {{\boldsymbol {\sigma }}:{\boldsymbol {\sigma }}}}={\sqrt {\sigma _{ij}\sigma _{ij}}}}$. 그 다음에 점성 변형률은 관계에 의해 주어진다.

${\displaystyle {\dot {\boldsymbol {\varepsilon }}}_{\mathrm {vp} }={\cfrac {\boldsymbol {\sigma }}{\lambda }}\left[{\cfrac { {\boldsymbol {\sigma }} }{\lambda }}\right]^{N-1}}$

1차원 형태로 노턴-호프 모델은 다음과 같이 표현할 수 있다.

${\displaystyle \sigma =\lambda ~\좌측({\dot {\barepsilon }}}_{\mathrm {vp}}}\우측)^{1/N}}$

$N{\displaystyle }$= ${\displaystyle 1}$.0${\displaystyle N=1.0}$일 때 고체는$$ 점탄성이 있다.

만약 우리가 플라스틱 흐름이 이소콜릭(볼륨 보존)이라고 가정한다면, 위의 관계는 보다 친숙한 형태로^[21] 표현될 수 있다.

${\displaystyle {\boldsymbol{s}}=2K~\왼쪽({\sqrt{3}}}{\dot {eq}\오른쪽)^{m-1}~{\dot {\boldsymbol{\vpsylon}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}"{\matmathmathrmathrmathrmathrmathrmathrmatm$

여기서 $s{\displaystyle \mathit{}}$ ${\$은(는) 일탈 스트레스 텐서, $\epsilon {\displaystyle {\stackrel{}{}}_{\mathrm{eq}}}$ ${\dot$ {\$dot {\varepsilon }}_{\mathrm${$eq$$}}}}}$은(는) 폰 미제스 등가 변형률이고$,$ $K{\displaystyle }$ , ${\displaystyle m}${\$disstyparam$. 등가 변형률은 다음과 같이 정의된다.

${\dot}{\bar {\bar {\epsilon }}={\sqrt {{}{2}{3}}{\bar {\bar {\epsilon }}}}}}은(는) {\bar {\bar {\bar {\epsilon }}}}}}}}}}}}}$

이러한 모델은 절대 용해점(켈빈 단위)의 3분의^[21] 2 이상의 온도에서 금속과 합금에 적용되며, 높은 온도에서 폴리머/아스팔트에도 적용할 수 있다. 그러한 물질의 변형률 강화, 크리프 및 이완 시험에 대한 반응은 그림 6에 나타나 있다.

그림 6: 경화, 크리프 및 이완 테스트에 대한 완벽한 점성 고체의 반응.

탄성 완전 점성 고체(Bingham-Norton 모델)

탄성-완벽하게 점성 모드를 구축하기 위해 두 가지 유형의 기본 접근법을 사용할 수 있다. 첫 번째 상황에서는 슬라이딩 마찰 요소와 대시팟이 병렬로 배열된 다음 그림 7과 같이 탄성 스프링에 직렬로 연결된다. 이 모델을 빙엄-맥스웰 모델(맥스웰 모델 및 빙엄 모델과 유사하게) 또는 빙엄-노튼 모델이라고 한다.^[22] 두 번째 상황에서는 세 가지 요소가 모두 병렬로 배치된다. 이러한 모델을 켈빈 모델과 유추하여 빙엄-켈빈 모델이라고 한다.

탄성-완벽한 점성 재료의 경우 탄성 스트레인은 더 이상 무시할 수 없는 것으로 간주되지 않지만 플라스틱 스트레인의 비율은 초기 항복 응력의 함수일 뿐 경화의 영향은 없다. 슬라이딩 요소는 변형률에 관계 없이 탄성 한계를 초과할 때 일정한 항복 응력을 나타낸다. 모델은 다음과 같이 표현될 수 있다.

${\displaystyle{\begin{정렬}&,{\boldsymbol{\sigma}}={\mathsf{E}}~{\boldsymbol{\varepsilon}}&&\mathrm{를}~\{\boldsymbol{\sigma}})<>\sigma _{y}\\&,{\dot{\boldsymbol{\varepsilon}}}={\dot{\boldsymbol{\varepsilon}}}_{\mathrm{e}}+{\dot{\boldsymbol{\varepsilon}}}_{\mathrm{vp}}={\mathsf{E}}^{)}~{\dot{\boldsymb.올{\sigma}}}와{\cfrac{\\chmbol{\eta }}}{{\\eta }}}왼쪽[1-{\\na _\na _{y}}\\\\\mathrm {for}~\\\\\\\\chibmbol {\}}\geq \y}\end{y}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 $\eta {\displaystyle }$ ${\displaystyle \eta }$은(는) 대시포트 요소의 점성이다. 대시보트 요소가 노턴 형식의 반응을 갖는 경우

${\displaystyle {\cfrac{\cfrac{\boldsymbol{\eta}}={\cfrac {\\lambda }}}}}{\cfrac {\\\boldsymbol{\}}}}{\lambda rigma ^{{{{N-}-}-N-}$

Bingham-Norton 모델을 구입하십시오.

${\displaystyle {\dot {\boldsymbol {\varepsilon }}}={\mathsf {E}}^{-1}~{\dot {\boldsymbol {\sigma }}}+{\cfrac {\boldsymbol {\sigma }}{\lambda }}\left[{\cfrac {\ {\boldsymbol {\sigma }}\ }{\lambda }}\right]^{N-1}\left[1-{\cfrac {\sigma _{y}}{\ {\boldsymbol {\sigma }}\ }}\right]\quad \mathrm {for} ~\ {\boldsymbol {\sigma }}\ \geq \sigma _{y}}$

변형률에 대한 다른 표현은 일반 형식을 가진 문헌에서도^[22] 관찰할 수 있다.

${\displaystyle {\dot {\boldsymbol {\varepsilon }}}={\mathsf {E}}^{-1}~{\dot {\boldsymbol {\sigma }}}+f({\boldsymbol {\sigma }},\sigma _{y})~{\boldsymbol {\sigma }}\quad \mathrm {for} ~\ {\boldsymbol {\sigma }}\ \geq \sigma _{y}}$

그러한 물질의 변형률 강화, 크리프 및 이완 시험에 대한 반응은 그림 8에 나타나 있다.

그림 8. 경화, 크리프 및 이완 테스트에 대한 탄성 완전 점성 고체의 반응.

탄소성 경화 고체

변형 경화가 있는 탄성-비스코플라스틱 소재는 완벽한 가소성을 가진 탄성-비스코플라스틱 소재와 유사한 방정식으로 설명된다. 그러나 이 경우 스트레스는 플라스틱 변형률과 플라스틱 변형률 자체에 따라 달라진다. 탄소성 탄소의 경우 항복 응력을 초과한 후 응력은 초기 항복점을 넘어 계속 증가한다. 이는 슬라이딩 요소의 항복응력이 스트레인에 따라 증가하며 모델은 다음과 같이 일반적인 용어로 표현될 수 있음을 의미한다.

ε)ε e)Er마다<>σ, σ yε ˙ = ε ˙ e+ε ˙ vp)E1σ ˙ −+f(σ,σ는 y,ε vp)σ frσ ≥σ는 y{\displaystyle{\begin{정렬}&, 거예요{\boldsymbol{\varepsilon}}){\boldsymbo 1σ)ε f−.L{\varepsilon}}_{\mathrm{e}}={\mathsf{E}}^{)}~{\boldsymbol{\sigma}}=~{\boldsymbol{\varepsilon}}&&\mathrm{를}일{\boldsymbol{\sigma}}<>\sigma _{y}\\&,{\dot{\boldsymbol{\varepsilon}}}={\dot{\boldsymbol{\varepsilon}}}_{\mathrm{e}}+{\dot{\boldsymbol{\varepsilon}}}_{\mathrm{vp}}={\mathsf{E}}^{)}~{\dot{\bolds.ymbol{\sigma}$}}}+f({\boldsymbol {\sigma }},\mama _{y}}{\\barembol {vp}}}}~{\boldsymbol {\\sigmatmembol}{\\mama}}{\geq$\ \$ma _{y}}}}}정렬$

이 모델은 금속과 합금이 중온 및 고온일 때 채택되고 높은 부하 하중의 목재일 때 채택된다. 그러한 소재의 변형률 강화, 크리프 및 이완 시험에 대한 반응은 그림 9와 같다.

그림 9. 경화, 크리프 및 이완 테스트에 대한 탄소성 경화의 반응.

변형률 종속 가소성 모델

작은 변종에 대한 고전적 현상학적 점성 모델은 보통 두 가지 유형으로 분류된다.^[3]

• 페르지나 제형
• 듀보-라이온스 공식

퍼지나 제형

Perzyna 공식에서 플라스틱 변형률은 형식의 구성적 관계에 의해 주어지는 것으로 가정한다.

${\displaystyle{\dot{\varepsilon}}_{\mathrm{vp}}={\cfrac{\left\langle f({\boldsymbol{\sigma}},{\boldsymbol{q}})\right\rangle}{\tau}}{\cfrac{\partial f}{\partial{\boldsymbol{\sigma}}}}={\begin{경우}{\cfrac{f({\boldsymbol{\sigma}},{\boldsymbol{q}})}{\tau}}{\cfrac{\partial f}{\partial{\boldsymbol{\sigma}}}}&{\rm{만약}}~f({\b.청소년들ymbol {\jamma }},{\\bmsymbol {q}})0\\\0&{\rm}\\case}}}$

where ${\displaystyle f(.,.)}$ is a yield function, ${\displaystyle {\boldsymbol {\sigma }}}$ is the Cauchy stress, ${\displaystyle {\boldsymbol {q}}}$ is a set of internal variables (such as the plastic strain ${\displaystyle {\boldsymbol {\varepsilon }}_{\mathrm {vp} }}$), ${\displa$$ystyle \tau }$은(는) 휴식 시간이다. 표기법 $⟨{\displaystyle }$… $⟩$ {\$displaystyle \langle \dots \rangele}$은 맥컬레이 대괄호를 나타낸다. 차보체 모델의 다양한 버전에서 사용되는 흐름 규칙은 페르지나의 흐름 규칙의^[23] 특수한 경우로서 그 형태를 가지고 있다.

${\dot}{\dot}}{\mathrm {vp}}}=\좌측\langle {\flac {f}{0}}\우측\rangele ^{n}({\mbcymbol {\}-{\chibmbol {\\chi }}}}}}}}}$

여기서 $f{\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은 $f{\displaystyle }$ ${\displaystyle f}$의 quasistatic 값이며$$, $\chi {\displaystyle \mathit{}}$ ${\$은(는) 백스트레스(백스트레스)이다$$. 백스트레스 모델도 차보체 모델이라는 이름으로 통한다.

듀보-리온스 공식화

듀보-라이온스 공식은 페르지나 공식과 동일하며 다음과 같이 표현될 수 있다.

${\displaystyle {\dot {\varepsilon }}_{\mathrm {vp} }={\begin{cases}{\mathsf {C}}^{-1}:{\cfrac {{\boldsymbol {\sigma }}-{\mathcal {P}}{\boldsymbol {\sigma }}}{\tau }}&{\rm {{if}~f({\boldsymbol {\sigma }},{\boldsymbol {q}})>0}}\\0&{\rm {otherwise}}\end{cases}}}$

여기서 $C{\displaystyle \mathsf{}}$ ${\$은(는) 탄성 강성 텐서, P ${\displaystyle \sigma \mathit{}}${\$displaystyle${\$mathcal{P}{\\boldsymbol{\sigma}}}$은 가능한 모든 탄성 응력 상태를 경계로 하는 영역의 경계에서 스트레스 상태의 가장 가까운 점 투영이다. $일반적$으로 P ${\${\$mathcal{P}{\boldsymbol{\sigma}}}$의 양은 비율에 구애받지 않는 솔루션에서 가소성 문제에 이르는 것으로 확인된다$$.

흐름 응력 모델

수량 $f{\displaystyle (\sigma \mathit{}}$,${\displaystyle q\mathit{}}$) ${\displaystyle f({\boldsymbol {\sigma }},{\boldsymbol{q})$는 항복면의 진화를 나타낸다$$. 항복함수 $f{\displaystyle }$ ${\displaystyle f}$은 종종 응력의 일부 불변성과 항복응력(또는 플라스틱 흐름응력)에 대한 모델로 구성된 방정식으로 표현된다$$. 폰 미제스(${\displaystyle {Von\mathrm{}}_{}}$Mises) $또는$ J 2 {\displaystyle $J_{2$} 가소성이$$ 그 예다. 그러한 상황에서 플라스틱 변형률은 비율에 독립적인 가소성과 같은 방식으로 계산된다. 다른 상황에서 항복 응력 모델은 플라스틱 변형률을 계산하는 직접적인 수단을 제공한다.

수많은 경험적 및 반감기적 흐름 응력 모델이 계산적 가소성을 사용한다. 다음 온도 및 변형률 종속 모델은 현재 사용 중인 모델의 샘플링을 제공한다.

1. 존슨-쿡 모델
2. 스타인버그-코크란-기난-룬드 모델
3. 제릴리-암스트롱 모델
4. 기계적 임계값 응력 모델
5. 프레스턴-양국-Tonks-Wallace 모델.

존슨-쿠크(JC) 모델은 순수하게 경험적이며 5개 모델 중 가장 널리 사용된다. 그러나 이 모델은 고온에서 비현실적으로 작은 변형률 의존성을 보인다. 스타인버그-코크란-기난-룬드(SCGL) 모델은 반감광적이다. 그 모델은 순전히 경험적이고 높은 변형률에서 독립적이다. 에 기초한 탈구 기반 확장은 낮은 변형률에서 사용된다. SCGL 모델은 충격물리학계에서 광범위하게 사용된다. Zerilli-Armstrong(ZA) 모델은 물리적으로 간단한 기반 모델로 광범위하게 사용되어 왔다. 탈구 역학으로부터 아이디어를 기반으로 한 보다 복잡한 모델은 MTS(Mechanical Threshold Stress) 모델이다.^[29] 이 모델은 구리, 탄탈룸,^[30] 강철 합금,^[31][32] 알루미늄 합금의 소성변형을 모형화하는 데 사용되어 왔다.^[33] 그러나 MTS 모델은 약 10⁷/s 미만의 변형률로 제한된다. 프레스턴-Tonks-Wallace(PTW) 모델도 물리적으로 기반을 두고 있으며 MTS 모델과 유사한 형태를 가지고 있다. 단, PTW 모델에는 과구동 충격 시스템(스트레인 레이트가 10⁷/s 이상)에서 소성 변형을 모델링할 수 있는 구성 요소가 있다. 따라서 이 모델은 5가지 흐름 응력 모델 중 가장 큰 범위의 변형률에 유효하다.

Johnson-Cook 흐름 응력 모델

존슨-쿡(JC) 모델은 순전히 경험적이며 흐름 스트레스에 대해 다음과 같은 관계를 제공한다(${\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\$

${\displaystyle {\text{(1)}}\qquad \sigma _{y}(\varepsilon _{\rm {p}},{\dot {\varepsilon _{\rm {p}}}},T)=\left[A+B(\varepsilon _{\rm {p}})^{n}\right]\left[1+C\ln({\dot {\varepsilon _{\rm {p}}}}^{*})\right]\left[1-(T^{*})^{m}\right]}$

여기서 $\epsilon {\displaystyle {}_{}}$ ${\displaystyle {p\mathrm{}}_{}}$ ${\$ {$p}}$은(는) 동등한 플라스틱 변형률이고, ${\displaystyle \epsilon }$ ${\displaystyle \stackrel{}{{p\mathrm{}}_{}}}$ ${\displaystyle \stackrel{}{{\dot{}}_{}}}$ p$display$ {\$dot {\varepsilon _{\rm{p}}}}$은(는) 플라스틱 변형률이며, $A{\displaystyle }$,${\displaystyle }$B ,${\displaystyle C}$ , ${\displaystyle m}$, C , m ${\displaystystystydisplaystytype A,$ C, C$,n}$은 ${\displaystyle \mathrm{물질}}$ 상수이다$$.

(1)식의 정규화된 변형률과 온도는 다음과 같이 정의된다.

${\displaystyle {\dot {\varepsilon _{\rm {p}}}}^{*}:={\cfrac {\dot {\varepsilon _{\rm {p}}}}{\dot {\varepsilon _{\rm {p0}}}}}\qquad {\text{and}}\qquad T^{*}:={\cfrac {(T-T_{0})}{(T_{m}-T_{0})}}}$

여기서 $\epsilon {\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{p\mathrm{}}_{}}}$ $˙{\$은 수율 및 경화 매개변수 A,B 및 n을 결정하는 데 사용되는 준 정전기 시험의 유효 플라스틱 변형률이다$$. 흔히 $just{\displaystyle {\stackrel{}{{}_{}}}^{}}$ ${\displaystyle {\stackrel{}{{p\mathrm{}}_{}}}^{}}$ ${\displaystyle {\ast }^{}}$ $∗{\$ 비차원을$$ 만들기 위한 매개 변수만 생각되는 경우가 많기 때문에 이것은 아니다.^[35] ${\displaystyle T_{}}$ ${\$은(는) 기준온도, ${\displaystyle {Tm}_{}}$ ${\$은(는) 기준용융온도다. < ${\displaystyle T^{*}<0}$이(가) 있는 조건의 경우 ${\displaystyle \mathrm{m}}$= 1 ${\displaystyle m=1}$이라고 가정한다$.$

스타인버그-코크란-기난-룬드 흐름 응력 모델

스타인버그-코크란-귀난-룬드(SCGL)^[25] 모델은 높은 변형률 상황을 위해 스타인버그 외가 개발한 반감광 모델이며, 스타인버그와 룬드가 저변형률 및 BCC 재료로 확장했다.^[26] 이 모델의 흐름 스트레스는

${\displaystyle {\text{(2)}}\qquad \sigma _{y}(\varepsilon _{\rm {p}},{\dot {\varepsilon _{\rm {p}}}},T)=\left[\sigma _{a}f(\varepsilon _{\rm {p}})+\sigma _{t}({\dot {\varepsilon _{\rm {p}}}},T)\right]{\frac {\mu (p,T)}{\mu _{0}}};\quad \sigma _{a}f\leq \sigma _{\text{max}}~~{\text{and}}~~\sigma _{t}\leq \sigma _{p}}$

where ${\displaystyle \sigma _{a}}$ is the athermal component of the flow stress, ${\displaystyle f(\varepsilon _{\rm {p}})}$ is a function that represents strain hardening, ${\displaystyle \sigma _{t}}$ is the thermally activated component of the flow stress, ${\displaystyle \mu (p$$,T)}$은 압력과 온도에 의존하는 전단계수이며, $\mu {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$ 스타일 $\mu _{0}$은 표준$$ 온도와 압력의 전단계수다. 피부 스트레스의 포화값은 $\sigma {\displaystyle {}_{}}$ ${\displaystyle {\text{max}}_{}}$ ${\$ 입니다$.$ 열활성 응력의 포화도는 Peierls 스트레스( ${\displaystyle {is}_{}}$ ${\displaystyle {}_{}}$ ${\$이다.$$ 이 모델의 전단 계수는 보통 스타인버그-코크란-기난 전단 계량 모델로 계산된다.

변형률 강화 함수(${\displaystyle }$ ${\displaystyle f}$)에는 다음 형식이 있음

${\displaystyle f(\varepsilon _{\rm {p})=[1+\barepsilon _{\rm {p}+\barepsilon _{\rm {p}i)]^{n}}}$

여기서 $\beta {\displaystyle }$, ${\displaystyle n}$ ${\displaystyle \beta,n}$은(는) 작업 강화 매개 ${\displaystyle {변수}_{}}$이고, $\epsilon {\displaystyle {}_{}}$ ${\displaystyle {p\mathrm{}}_{}}$ i ${\displaystyle \var렙실론 _{\rm {p}i}$은(는) 초기 동등한 플라스틱 변형률이다.

열성분(${\displaystyle {}_{}}$ ${\displaystyle {tt}_{}}$ ${\$은 다음 방정식의 이분법 알고리즘을 사용하여 계산한다.^[26][27]

${\dottyle {\dot {\barepsilon _{\rm {p}}=\좌측[{\frac {1}{1}}}\exp \좌측[{\frac {2]U_{k}}{k_{b}~T}}\{{\frac{\sigma _{t}{\sigma _{p}}\right)^{2}\p}+{\frac {C_{2}}:{\sigma _{t}\{t}}}\quad \sigma _{t}\leq \sigma _{p}}}}}}}}}}}}}}}}}}}}}}}}}}$

여기서 $2{\displaystyle \mathrm{}}$ ${\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$${k$$}}$는 길이 ${\displaystyle L_{}}$ $d {\$의 탈구 부분에서 꼬임 구멍을 형성하는 에너지$$,$$${\displaystyle k_{}}$ b ${\$는 볼츠만 상수, ${\displaystyle {\sigma }_{}}$ p ${\$는 피에를 응력한다. 상수 $C{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}은 관계에 의해 주어진다$$.

${\displaystyle C_{1}:={\frac {\rho_{d}ab^{2}\nu{2w^{2}}:\quad C_{2}:={\frac {D}{\rho_{d}b^{2}}:}}}}}}$

여기서 ${\displaystyle {\rho }_{}}$ d ${\$는 탈구 밀도, ${\displaystyle L_{}}$ d ${\$는 탈구 세그먼트의 길이$$, ${\displaystyle$a}은 Peierls 계곡 사이의 거리, $b{\displaystyle }$ ${\$$displaystyle$$b}$은 버거 벡터의 크기, $\nu {\displaystyle }$ ${\$daystyeprequeneprequenepreadquenc$.$${\displaystyle w}$ ${\displaystyle w}$은(는) 꼬임 루프의 폭이고, $D{\displaystyle }$ ${\displaystyle D}$은(는) 드래그 계수다.

제릴리-팔스트롱 흐름 응력 모델

Zerilli-Armstrong(ZA) 모델은 단순화된 탈구 역학을 기반으로 한다. 흐름 응력에 대한 방정식의 일반적인 형태는

${\displaystyle {\text{}}}\qquad \sigma _{{\rm {p},{\rm {p},T)=\sigma _{a}+B\exp(-\beta T)++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++B_{0}{\sqrt}{\barepsilon _{\rm {p}}}\exp(-\alpha T)~~}$

이 모델에서 ${\$는 흐름 응력의 피부 성분이다$$.

$\displaystyle \sigma _{a:=\sigma _{g}+{\frac {k_{h}{\sqrt{l}}+K\varepsilon _{\rm{p}^{n}}}}$

여기서 $\sigma {\displaystyle {}_{}}$ ${\displaystyle g_{}}$ ${\$$displaystyle$ $\sigma_{g}$는 용액과 초기 탈구 밀도에 의한 기여, ${\displaystyle k_{}}$ h ${\$는 미세구조 응력 강도, $l{\displaystyle }$ ${\displaystyle l}$은 평균 곡물 직경, $K{\displaystyle }$ ${\displaystystyle K}$은 FC 소재는 0, $B{\displaystyle ,}$ ${\displaystyle {B\mathrm{}}_{}}$, B, B, B, B, B, B,$B_{0$}$}}}$은(는) 재료 상수다.

열활성 항에서 지수 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$ 및$$ $\beta {\displaystyle }$ ${\displaystyle \beta }$의 함수 형태는 다음과$$ 같다.

${\displaystyle \cHB =\l0}-\cHB _{0}-\lndot\dot{\rm{p}}};\cHB \cHB _{0}-\ln\\dot{\barepsilon _{\rm {p}};;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;}$

여기서 $\alpha {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}{}_{}{}_{}}$ 1 , ${\displaystyle {\beta \mathrm{}}_{}}$ 0${\displaystyle {}_{}}$ ${\displaystyle {\beta \mathrm{}}_{}}$ 1$${\$displaystyle$\ _ $_{0$}, $},_{$1},$beta_{0$}, beta_{0$}, beta_{1$}는 재료 유형( (, bccp, hcp, 합금)에 따라 달라지는 재료 매개변수다$$. Zerilli-Armstrong 모델은 고온에서 더 나은 성능을 위해 변형되었다.

기계적 임계값 응력 흐름 응력 모델

MTS(Mechanical Threshold Stress) 모델에는 다음과 같은 형식이 있다.

${\displaystyle {\text{}}\qquad \sigma _{{\rm{p}},{\dot {\barepsilon }}},T)=\sigma _{a}+(S_{i}\sigma_{i}+)S_{e}\sigma _{e}{\frac {\mu(p,T)}{\mu _{0}}}}{\mu _{0}}}}}}}$

여기서 ${\$는 기계적 임계값 응력의 피부 성분이고, ${\displaystyle i_{}}$ i$${\$displaystyle \mama _{$i}는 열활성$$ 탈구 운동과 탈구-탈구 상호작용에 대한 내적 장벽으로 인한 흐름 응력의 성분이며, , ${\displaystyle e_{}}$ ${\${e_{e_{$e}$은 c이다$$.변형(스트레인 강화)이 증가하는 미세구조적 진화로 인한 흐름 응력을 배제하고(${\displaystyle {Si}_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$는 온도 및 변형률에 따른 스케일링 인자로, μ ${\displaystyle {0\mathrm{}}_{}}$ ${\$은 0K 및 주변 압력에서의 전단계수이다.

스케일링 요인은 Arrhenius 형태를 취한다.

${\displaystyle {\reasoned}S_{i}&=\좌측[1-\좌측({\frac {k_{b}).T}{g_{0i}b^{3}\mu(p,T)}}}\ln {\frac {\barepsilon _{0}}{\rm{0}}}{\\dot{\varepsilon }}}}}}}^{1/q_{i}\}\}\\\\\S_{e}&=\좌측[1-\좌측({\frac {k_{b}).T}{g_{0e}b^{3}\mu(p,T)}}\ln {\frac {\dot {\varepsilon _{0}}{\rm{0}}}{\barepsilon }}}\right)^{1/q_{e}}^{1/p_{e}}}}}}}}}}}}}}}}}}}}}{liged}}}}}}{liged}}}}}}}}}}}}}}}}}}}}}}$

where ${\displaystyle k_{b}}$ is the Boltzmann constant, ${\displaystyle b}$ is the magnitude of the Burgers' vector, (${\displaystyle g_{0i},g_{0e}}$) are normalized activation energies, (${\displaystyle {\dot {\varepsilon }},{\dot {\varepsilon _{\rm {0}}}}}$) are 변형률 및 기준 변형률 및 (${\displaystyle {qi}_{}}$, ${\displaystyle p_{}}$ ${\displaystyle {}_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle e_{}}$, ${\displaystyle {}_{}}$ e , p ${\displaystyle e_{}}$ ${\$p_${e$은 상수다.

기계적 임계값 응력의 변형률 강화 성분(${\displaystyle {}_{}}$ ${\displaystyle e_{}}$ ${\$은 경험적으로 수정된 Voce 법칙에 의해 주어진다.

${\displaystyle {\text{}}}\qquad {d\pamma_{e}{d\varepsilon _{\rm{p}}}=\theta(\chma _{e}})}$

, where

${\displaystyle {\begin}\theta(\sigma _{e})\theta_{0}[1-F(\sigma _{e})]+\theta_{0}&=a_{0}+a_{1]}}\ln {\dot {\varepsilon _{\rm{p}}}+a_{2}}}{\sqrt {\dot {\bar렙실론 _{\rm {p}}}-a_{3}T\\F(\sigma _{e})&={\cfrac {\tanh \left(\alpha {\cfrac {\sigma _{e}}{\sigma _{es}}}\right)}{\tanh(\alpha )}}\\\ln({\cfrac {\sigma _{es}}{\sigma _{0es}}})&=\left({\frac {kT}{g_{0es}b^{3}\mu(p,T)}}}\right)\ln \ln({\cfrac {\dot {\varepsilon _{\rm{p}}}}{\barepsilon _{\rm{p}}}}}\ended}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

$and{\displaystyle {}_{}}$ ${\$는 탈구 축적으로 인한 경화, $\theta {\displaystyle {}_{}}$ ${\displaystyle I_{}}$ ${\displaystyle V_{}}$ ${\$$IV}}$ is the contribution due to stage-IV hardening, (${\displaystyle a_{0},a_{1},a_{2},a_{3},\alpha }$) are constants, ${\displaystyle \sigma _{es}}$ is the stress at zero strain hardening rate, ${\displaystyle \sigma _{0es}}$ is the saturation threshold stress for 0K에서의 $변형{\displaystyle {}_{}}$, ${\displaystyle {g\mathrm{}}_{}}$ ${\displaystyle 0_{}}$ ${\displaystyle e_{}}$s {\$displaystyle g_${0es$}}$은 상수, $and{\displaystyle \stackrel{}{{}_{}}}$ ${\displaystyle \stackrel{}{{p\mathrm{}}_{}}}$ ${\displaystyle \stackrel{}{{\dot{}}_{}}}$ p p ${\dot {\varepsilon _{\rm{p}}}}$은 최대 변형률이다. 최대 변형률은 보통 약 ${\displaystyle {10\mathrm{}}^{}}$ 7 ${\$s로 제한된다.

프레스턴-Tonks-Wallace 흐름 응력 모델

프레스턴-Tonks-Wallace(PTW) 모델은 극한 변형률(최대 10¹¹/s)과 용해까지의 온도에 대한 흐름 응력에 대한 모델을 제공하려고 시도한다. 모델에는 선형 Voce 강화 법칙이 사용된다. PTW 흐름 응력은 다음에 의해 주어진다.

${\displaystyle{\text{(6)}}\qquad \sigma _ᆮᆪ=ᆯ2\left[\tau_{s}+\alpha\ln \left는 경우에는 1-\varphi \exp \left(-\beta-{\cfrac{\theta \varepsilon_{\rm{p}}}{\alpha \varphi}}\right)\right]\right]\mu(p,T)&,{\text{열적 정권}}_{s}\mu(p,T)& \\2\tau,{\text{충격 체제}}\end{ca.이}}}$

와 함께

${\displaystyle \prox :={\frac {s_{0}-\tau _{y}}{s}-\tau _{s}-{s}}};\parpi :=\exp(\cHB )-1}$

where ${\displaystyle \tau _{s}}$ is a normalized work-hardening saturation stress, ${\displaystyle s_{0}}$ is the value of ${\displaystyle \tau _{s}}$ at 0K, ${\displaystyle \tau _{y}}$ is a normalized yield stress, ${\displaystyle \theta }$ is the hardening constant in the Voce harde닝 법칙, $d{\displaystyle }$ ${\displaystyle d}$은(는) Voce 강화 법칙을 수정하는 치수 없는 재료 매개 변수다.

포화 응력 및 항복 응력은 다음에 의해 주어진다.

${\displaystyle{\begin{정렬}\tau _{s}&, =\max \left\ᆭ-ᆩᆮ\left[\kappa{\hat{T}}\ln \left({\cfrac{\gamma{\dot{\xi}}}{\dot{\varepsilon_{\rm{p}}}}}\right)\right],s_ᆯ\left({\cfrac{\dot{\varepsilon_{\rm{p}}}}{\gamma{\dot{\xi}}}}\right)^{s_{1}}}}\right\}\\\tau _{y}&, =\max \left\{y_{0}-(y_{0}-y_{\in.fty}){)rm {{erf}\left[\kappa {\hat {T}}\ln \left({\cfrac {\gamma {\dot {\xi }}}{\dot {\varepsilon _{\rm {p}}}}}\right)\right],\min \left\{y_{1}\left({\cfrac {\dot {\varepsilon _{\rm {p}}}}{\gamma {\dot {\xi }}}}\right)^{y_{1},s_{0}\좌측\({ac {\dot{p}}}{\rm {p}}}{\barepsilon _{\rm {p}}}}}{\dot{\xi }}\right\}}^{s_}}}}$

where ${\displaystyle s_{\infty }}$ is the value of ${\displaystyle \tau _{s}}$ close to the melt temperature, (${\displaystyle y_{0},y_{\infty }}$) are the values of ${\displaystyle \tau _{y}}$ at 0 K and close to melt, respectively, ${\displaystyle (\kappa ,\gamma )}$$$ 재료 상수, $T{\displaystyle \stackrel{}{}^}$ =${\displaystyle T}$ / ${\displaystyle T_{}}$ m$${\$displaystyle {\T}=T_{m$ (${\displaystyle {s\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ 1, ${\displaystyle {}_{}}$ 1,${\displaystyle {}_{}}$y ${\displaystyle {2\mathrm{}}_{}}${\$displaystyle s_{1},y_{1},y_{$2$\}\})$는 높은 변형률 체계에 대한 재료 매개변수이며,

${\dot {\xi }={\frac {1}{1}:{2}}:\왼쪽 사진\pi \rho}{3}M}\오른쪽)^{1/3}\왼쪽({\cfrac {\mu(p,T)}{\rho }}}{\rho }}{1/2}}$

$여기$서 $\rho {\displaystyle }$ ${\displaystyle \rho }$은$$ 밀도, M ${\displaystyle M}$은 원자 질량이다.

참고 항목

• 점탄성
• 빙엄 플라스틱
• 대쉬팟
• 크리프(변형)
• 가소성(물리학)
• 연속체 역학
• 준고체

참조