다면군

3차원의 점 그룹
다면군, [n,3], (*n32)
비자발적 대칭 C_s, (*) [ ] =	순환 대칭 C_nv, (*n) [n] =	치측 대칭 D_nh, (*n22) [n,2] =
사면 대칭 T_d, (*332) [3,3] =	팔면 대칭 O_h, (*432) [4,3] =	이코사면 대칭 I_h, (*532) [5,3] =

기하학에서 다면체는 플라토닉 고형물의 대칭 그룹 중 하나이다.

무리

3개의 다면체 그룹이 있다.

순서 12의 사면 그룹, 일반 사면체의 회전 대칭 그룹. 그것은₄ A와 이형이다.
- T의 결합 등급은 다음과 같다.
  - 정체성
  - 4 × 120° 회전, 주문 3, cw
  - 4 × 120° 회전, 주문 3, ccw
  - 3 × 180° 회전, 순서 2
순서가 24인 팔면 그룹, 큐브의 회전 대칭 그룹 및 정규 팔면 그룹. 그것은₄ S와 이형이다.
- O의 결합 등급은 다음과 같다.
  - 정체성
  - 정점을 중심으로 ±90°만큼 6 × 회전, 순서 4
  - 8 × 삼각형 중앙을 중심으로 ±120° 회전, 순서 3
  - 3 × 정점을 중심으로 180° 회전, 순서 2
  - 6 × 가장자리 중간점 주위로 180° 회전, 순서 2
순서가 60인 이도사면군, 일반 도두면체와 일반 이도사면체의 회전대칭군. 그것은₅ A와 이형이다.
- 내가 배우는 연애 수업은 다음과 같다.
  - 정체성
  - 12 × ±72° 회전, 순서 5
  - 12 × ±3° 회전, 5를 주문하다
  - 20 × ±120° 회전, 3번 주문하다
  - 15 × 180° 회전, 순서 2

이러한 대칭은 전체 반사 그룹에 대해 각각 24, 48, 120으로 두 배가 된다. 반사 대칭은 각각 6, 9, 15개의 거울을 가지고 있다. 팔면 대칭인 [4,3]은 6개의 사면 대칭[3,3] 거울과 3개의 이면 대칭 Dih₂, [2,2]의 결합으로 볼 수 있다. 화두 대칭은 사두 대칭의 또 다른 두 배다.

완전 사면 대칭의 결합 등급인_d TsS는₄ 다음과 같다.

정체성
8××120° 회전
3 × 180° 회전
두 개의 회전 축을 통한 평면에서의 6 × 반사
6 × 회전 선택 X 90°

피리토헤드 대칭의 결합 등급 T는_h T의 결합 등급을 포함하며, 4의 두 등급이 결합되고 각각은 반전된다.

정체성
8××120° 회전
3 × 180° 회전
역전의
8 × 60° 회전 선택
평면에 3 × 반사

전체 팔면체군(O_h,S₄ × C)의₂ 결합 등급은 다음과 같다.

역전의
6 × 회전 선택 X 90°
8 × 60° 회전 선택
4배 축에 수직인 평면에서 3 × 반사
2-폴드 축에 수직인 평면에서 6 × 반사

완전 동면 대칭의 결합 등급인_h IaA₅ × C도₂ 각각 반전된 것을 포함한다.

역전의
12 × 108° 회전 선택, 주문 10
12 × 36° 회전 선택, 10 주문
20 × 60° 회전 선택, 주문 6
15 × 반사, 순서 2

키랄 다면체군

키랄 다면체군
이름 (오르브)	콕시터 표기법	주문	추상적 구조화하다	회전 포인트 #_valence	도표
이름 (오르브)	콕시터 표기법	주문	추상적 구조화하다	회전 포인트 #_valence	직교	입체적
T (332)	[3,3]⁺	12	A을₄	4₃ 3₂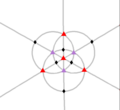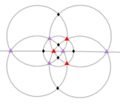
T_h (3*2)	[4,3⁺]	24	A₄×2	4₃ 3_*2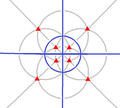
O (432)	[4,3]⁺	24	S₄	3₄ 4₃ 6₂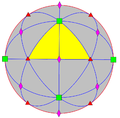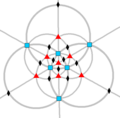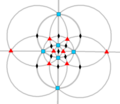
I (532)	[5,3]⁺	60	A을₅	6₅ 10₃ 15₂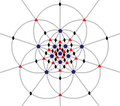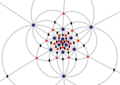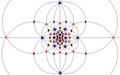

전체 다면체 그룹

전체 다면체 그룹
바일 쇼에. (오르브)	콕시터 표기법	주문	추상적 구조화하다	콕시터 번호를 붙이다 (h)	거울 (m)	미러 다이어그램
바일 쇼에. (오르브)	콕시터 표기법	주문	추상적 구조화하다	콕시터 번호를 붙이다 (h)	거울 (m)	직교	입체적
A을₃ T_d (*332)	[3,3]	24	S₄	4	6
B₃ O_h (*432)	[4,3]	48	S₄×2	8	3 6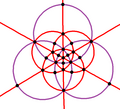
H₃ I_h (*532)	[5,3]	120	A₅×2	10	15