최적성 이론

이 글에는 국제음반문자(IPA)의 음성 표기가 실려 있다. IPA 기호에 대한 소개 가이드는 도움말을 참조하십시오.IPA. [ ], / 및 ⟨ ⟩의 구별은 IPA § 브래킷 및 전사 구분자를 참조하십시오.

언어학에서 Optimality 이론(자주 OT로 약칭)은 관찰된 형태의 언어가 상충되는 제약조건의 최적의 만족도에서 발생한다는 것을 제안하는 언어학 모델이다. OT는 일반적으로 제약보다는 규칙을 사용하는 자동분할음운학, 선형음운학(SPE)과 같은 음운학적 분석에 대한 다른 접근법과 다르다. OT 모델은 입력에서 출력까지의 매핑을 제공하는 시스템으로서 그래머를 사용한다. 일반적으로 입력은 기초적인 표현으로, 출력은 표면 실현으로 간주된다. 그것은 생성 문법의 더 큰 틀 안에서 접근하는 것이다.

언어학에서 Optimality 이론은 Alan Prince와 Paul Smolensky가 1991년에^[1] 한 강연에서 기원을 두고 있으며, 후에 1993년에 같은 작가들에 의해 책 원고로 개발되었다.^[2]

개요

그 이론에는 세 가지 기본 요소가 있다.

제너레이터 (Gen)을 입력하여 가능한 출력물 또는 지원자의 목록을 생성한다.
구속조건 구성요소(Con)는 엄격히 분류된 위반 가능한 제약조건의 형태로 후보자 간 결정에 사용되는 기준을 제공한다.
평가자(Evaluator)는 제약조건에 따라 최적의 후보를 선택하며, 이 후보가 산출물이다.

Optimality 이론은 이러한 요소들이 보편적이라고 가정한다. 문법의 차이는 보편적 제약 조건인 Con의 다른 순위를 반영한다. 언어 습득의 일부는 이러한 제약조건의 순위를 조정하는 과정이라고 설명할 수 있다.

언어에 적용되는 Optimality 이론은 원래 언어학자 Alan Prince와 Paul Smolensky에 의해 1991년에 제안되었고, 후에 Prince와 John J. McCarthy에 의해 확대되었다. Optimality 이론에 대한 많은 관심은 Optimality 이론이 처음 적용된 영역인 음운학에서 그것의 사용과 관련이 있지만, 이 이론은 언어학의 다른 하위 분야(예: 구문 및 의미론)에도 적용된다.

Optimality 이론은 보편적 원리, 언어 유형학, 언어 습득의 연구에 초점을 맞춘 다른 생성 문법 이론과 같다.

Optimality 이론은 신경망 연구에도 뿌리를 두고 있다. 1990년 제랄딘 레전드레, 미야타 요시로, 폴 스몰렌스키가 개발한 하모니크 문법의 연결론 대안으로 부분적으로 생겨났다. 연결론적 가중 제약조건을 가진 최적성 이론의 변형은 보다 최근의 연구에서 계속 추구되고 있다(Pater 2009).

입력 및 일반: 후보 세트

Optimality 이론은 입력에 언어별 제한이 없다고 가정한다. 이것을 기지의 풍요로움이라고 한다. 모든 문법은 가능한 모든 입력을 처리할 수 있다. 예를 들어 복잡한 클러스터가 없는 언어는 /flask/와 같은 입력을 처리할 수 있어야 한다. 복잡한 클러스터가 없는 언어는 이 문제를 어떻게 해결할지에 따라 다르다; 어떤 언어는 이 문제를 어떻게 해결할 것인가에 따라 에펜스(예: [팔라삭], 또는 모든 코다가 금지된 경우 [팔라사카])를 할 것이고, 어떤 언어는 삭제(예: [fas], [fak]), [las], [lak]를 할 것이다.

Gen은 입력에서 많이 벗어나더라도 출력 후보를 얼마든지 생성할 수 있다. 이것을 분석의 자유라고 한다. 언어의 문법(제한조건의 순위)에 따라 Eval에서 최적으로 평가할 대상자가 결정된다.^[3]

Con: 제약 조건 집합

최적성 이론에서는 모든 제약이 보편적이다. Con은 모든 언어에서 동일하다. 구속조건에는 두 가지 기본적인 유형이 있다.

충실도 제약조건은 관찰된 표면 형태(출력)가 어떤 특정한 방법으로 기초 또는 어휘 형태(입력)와 일치하도록 요구한다. 즉, 이러한 제약조건은 입력과 출력 형태 사이의 정체성을 요구한다.
표시성 제약조건은 출력의 구조적 양호한 형태에 대한 요건을 부과한다.

각자가 그 이론에서 결정적인 역할을 한다. 표시성 제약조건은 기초적인 형태로부터의 변화에 동기를 부여하며, 충실성 제약조건은 모든 입력이 완전히 표시되지 않은 형태(예: [ba])로 실현되는 것을 방지한다.

Con의 보편적인 성격은 언어유형에 대한 몇 가지 즉각적인 예측을 한다. 만약 그 문법이 Con의 다른 순위를 가짐으로써만 다르다면, 가능한 인간 언어의 집합은 존재하는 제약조건에 의해 결정된다. Optimality 이론은 Con의 순위에 대한 순열보다 더 많은 그래머가 있을 수 없다고 예측한다. 가능한 순위의 수는 총 제약 조건 수의 요인 수와 같으므로 요인 유형이라는 용어를 발생시킨다. 그러나 모든 제약조건이 모든 언어에서 관찰 가능한 효과를 보장하지는 않기 때문에 이러한 잠재적 문법들을 모두 구별하는 것은 불가능할 수 있다. Con의 제약조건에 대한 두 개의 총 주문은 동일한 범위의 입력-출력 매핑을 생성할 수 있지만, 서로 충돌하지 않는 두 제약조건의 상대적 순위는 다르다. 이 두 순위를 구분할 방법이 없기 때문에 그들은 같은 문법에 속한다고 한다. OT의 문법은 항이마트로이드(Merchant & Riggle 2016)에 해당한다. 동점 순위가 허용될 경우, 가능성 수는 요인보다는 순서가 정해진 벨 번호로, 훨씬 더 많은 수의 가능성을 허용한다.^[4]

충실도 제약

매카시 앤 프린스(1995)는 다음과 같은 충실한 제약을 받는 세 가지 기본 가문을 제안한다.

Max는 ("최대"에서) 삭제를 금지한다.
Dep은 ("의존적"으로부터) 경구(epential)를 금지한다.
식별자(F)는 형상 F의 값에 대한 변경을 금지한다("동일적"에서).

각 제약조건의 명칭은 "-IO" 또는 "-BR"로 혼합될 수 있으며, 각각 입력/출력 및 베이스/저감제(원하는 경우 후자는 환원분석에 사용된다)를 나타낸다. Identity-IO(음성)에서와 같이 Identified(F)에서 F는 구별되는 형상의 이름으로 대체된다.

맥스와 뎁은 프린스앤스몰렌스키(1993)가 제안한 파스와 필을 대체하며, '하위 세그먼트는 음절 구조로 구문 분석해야 한다'와 '표현 가능한 포지션은 기초 세그먼트로 채워져야 한다'고 각각 명시했다.^[5]^[6] 파스(Parse)와 채우기(Fill)는 기본적으로 맥스(Max)와 디프(Dep)와 동일한 기능을 제공하지만, 입력과 출력 사이의 관계가 아닌 출력만을 평가한다는 점에서 차이가 있으며, 이는 오히려 표시성 제약의 특징이다.^[7] 이것은 격납 이론으로 알려진 Prince & Smolensky가 채택한 모델에서 비롯된다. 이 모델은 출력에 의해 실현되지 않은 입력 세그먼트가 제거되는 것이 아니라 음절로 "비포장된 채로 내버려둔다"고 가정한다.^[8] 대응 이론으로 알려진 매카시 앤 프린스(1995, 1999년)가 내놓은 모델은 이후 이를 표준 틀로 대체했다.^[6]

매카시 앤 프린스(1995)도 다음과 같이 제안한다.

단어 또는 형태소 내부 세그먼트를 삭제할 때 위반되는 I-Contig. ("입력-내부"에서)
세그먼트를 단어 또는 형태소(내부적으로 "출력-내용"에서) 삽입할 때 위반되는 O-Contigue;
일부 세그먼트의 순서를 변경할 때 위반되는 선형성(즉, 메타텍스 금지)
둘 이상의 세그먼트가 하나로 실현될 때 위반되는 균일성(즉, 융합을 금지)
한 세그먼트가 여러 세그먼트로 실현될 때 위반되는 무결성(즉, Unpacking 또는 모음 파괴 금지 - Uniformity of Uniformity)

표시성 제약 조건

Prince & Smolensky(1993)에 의해 도입된 현저성 제약조건은 다음과 같다.

이름	성명서	기타 이름
누크	음절은 핵이 있어야 한다.
-코다	음절에는 코다가 없어야 한다.	노코다
온스	음절은 반드시 상쇄가 있어야 한다.	시작
HNuc	핵 부분은 ("화핵"으로부터) 다른 부분보다 더 음성이 높아야 한다.
*복잡한	음절은 V, CV 또는 VC여야 한다.
코다콘드	코다 자음은 시작 자음으로 공유되지 않는 특징을 가질 수 없다.	코다컨덕트
비Finality	단어의 마지막 음절(또는 발)은 스트레스를 받아서는 안 된다.	논핀
ftBin	발은 두 음절이어야 한다.	풋비너리티
Pk-Prom	가벼운 음절은 강조되어서는 안 된다.	피크프로맨스
WSP	중음절은 반드시 강조되어야 한다("무게 대 스트레스 원리").	무게-스트레스

문학의 정확한 정의는 다양하다. 일부 제약조건은 "커버 제약조건"으로 사용되기도 하는데, 이는 완전히 알려져 있지 않거나 중요하지 않은 제약조건의 집합에 해당한다.^[9]

일부 표시성 제약조건은 문맥이 없고 다른 것은 문맥에 민감하다. 예를 들어, *V는_nasal 모음이 어떤 위치에서 비음이어서는 안 되며 따라서 문맥이 없어야 한다고 말하는 반면, *VN은_oral 모음이 tautosyellabic 비음 앞에 있을 때는 구강이어서는 안 되며 따라서 문맥에 민감하다고 말한다.^[10]

정렬 제약 조건

로컬 접속사

두 제약조건은 하나의 제약조건으로 결합될 수 있는데, 이 제약조건은 지역 접속사라 불리며, 세그먼트, 음절 또는 단어와 같이 주어진 영역 내에서 두 제약조건이 모두 위반될 때마다 하나의 위반만을 준다. 예를 들어, [NoCoda & VOP]_segment는 코다에서 음성 산부인과당 한 번 위반되며("VOP"는 "음성 산부인과 금지"를 나타냄), *VoiseCoda로 동등하게 표기될 수 있다.^[11]^[12] 국소 접속사는 체인 이동을 분석할 때 발생하는 음운론적 불투명성 문제를 회피하는 방법으로 사용된다.^[11]

평가: 최적성 정의

원안에서는 A와 B 두 후보를 놓고 볼 때 A가 B보다 위반 횟수가 적으면 B가 구속조건인 것보다 낫거나 '화합성'이 더 낫다. A 후보가 A와 B를 구분하는 최상위 구속조건의 위반이 적은 경우 전체 구속조건 계층에서 B 후보보다 조화롭다. A는 다른 모든 후보들보다 제약 서열에서 더 나은 경우 후보 집합에서 "최적"이다. 그러나 이 평가의 정의는 규칙성을 초과하는 관계를 모델링할 수 있다.^[13]

For example, given the constraints C₁, C₂, and C₃, where C₁ dominates C₂, which dominates C₃ (C₁ ≫ C₂ ≫ C₃), A beats B, or is more harmonic than B, if A has fewer violations than B on the highest ranking constraint which assigns them a different number of violations (A is "optimal" if A beats B and the candidate set comprises only A and B). 만약 A와 B가₁ C에 동점이지만 A가 C에₂ B보다 더 잘한다면, A가 B보다₃ C에 대한 위반이 더 많더라도 A가 최적이다. 이 비교는 흔히 탁자와 함께 설명된다. 포인팅 핑거는 최적의 후보를 표시하며, 각 셀에는 주어진 후보 및 제약조건에 대한 위반별 별표가 표시된다. 후보자가 자신을 구분하는 최상위 제약조건에서 다른 후보보다 못한 행동을 하면 치명적인 위반(표에는 느낌표와 하위 제약조건에 대한 음영 셀로 표시)을 발생시킨다. 일단 한 후보가 치명적인 위반을 일으킨다면, 그것이 나머지 콘의 다른 후보들을 능가한다고 해도, 그것은 최적이 될 수 없다.

탁아우
입력		제약조건 1	제약2길	제약3길
a. ☞	A 후보	*	*	***
b	B 후보	*	**!

기타 공칭적 규약에는 순위가 정해지지 않았거나 같은 등급의 제약조건 열을 구분하는 점선, 잠정 순위 표고에 손가락 대신 체크 표시 ✔, 승자의 위반을 나타내는 동그라미 모양의 별표가 있다. 출력 후보에서 각괄호 ⟨ ⟩ ⟩은 세그먼트 e를 나타낸다.음성 인식에 편중되어 있으며, □와 □는 각각 인식 자음과 모음의 의미를 나타낸다.^[14] "much than" 기호 sign(때로는 내포된 ⪢)은 다른 것("C₁ ≫ C₂" = "C가₁ C를₂ 지배한다")에 대한 제약의 지배를 나타내는 반면, "수행" 연산자 ≻는 출력 후보("A ≻ B" = "A가 B보다 더 조화롭다")^[15]에 비해 우수한 조화를 나타낸다.

제약은 엄격한 지배의 서열로 분류된다. 엄격한 지배의 엄격함은 비록 두 번째 후보가 다른 모든 하위권 제약에 대해 더 나쁘게 평가했더라도 상위권 제약만을 위반하는 후보가 하위권 제약에 대해 더 나쁜 평가를 내리더라도 그렇지 않은 후보보다 계층에 더 나쁜 영향을 끼친다는 것을 의미한다. 이것은 또한 제약조건을 위반할 수 있다는 것을 의미한다; 어떤 제약조건에서 승리자보다 더 잘 하는 어떤 경쟁후보에 한해서, 승리자(즉, 가장 조화로운) 후보는 모든 제약조건을 만족시킬 필요가 없다. 승자가 그 경쟁자보다 더 잘 하는 상위권 제약조건이 있다. 언어 내에서 제약조건은 항상 준수될 정도로 충분히 높은 순위를 매길 수 있고, 관찰할 수 있는 효과가 없을 정도로 낮은 순위를 매길 수 있다. 또는 중간 순위를 매길 수 있다. 표시되지 않은 상태의 출현이라는 용어는 표시성 제약이 중간 순위를 가지므로 어떤 형태로든 위반되지만 그럼에도 불구하고 상위 제약 조건이 무관할 때 관측 가능한 효과를 갖는 상황을 기술한다.

매카시앤프린스(1994)가 제시한 초기 예는 음절이 자음으로 끝나는 것을 금지하는 제약 노코다다다(NoCoda)이다. 발랑가오에서 노코다는 타이난(입력을 충실히 이행하면 최종 /n/이 삭제되지 않음)과 같은 뿌리에서 보듯이 항상 복종할 만큼 순위가 높지 않다. 그러나 축소된 형태인 ma-tayna-taynan '반복적으로 뒤에 남겨져 있다'에서는 최종 /n/은 복사되지 않는다. 매카시 앤 프린스의 분석에 따르면, 이는 입력에 대한 충실도가 환원 재료에는 적용되지 않기 때문이며, 따라서 노코다는 가상의 마타이난-타이난(노코다 추가 위반이 있는)보다 마타이나-타이난(ma-tayna-taynan)을 자유롭게 선호하기 때문이다.

일부 최적성 이론가들은 프린스(2002b)에서 설명한 바와 같이 비교 표고의 사용을 선호한다. 비교 테이블aux는 고전 또는 "플라이스펙" 테이블aux와 동일한 정보를 표시하지만, 정보는 가장 중요한 정보를 강조할 수 있는 방식으로 제시된다. 예를 들어, 위의 표는 다음과 같은 방식으로 제공될 것이다.

비교 테이블라우
	제약조건 1	제약2길	제약3길
A~B	e	W	L

비교표에서 각 행은 개별 후보가 아닌 승자와 로저 쌍을 나타낸다. 제약조건이 승자와 로저 쌍을 평가하는 셀에서, 해당 열의 제약조건이 승자를 선호할 경우 "W"를, 제약조건이 패자를 선호할 경우 "L"을, 제약조건이 쌍을 구별하지 못할 경우 "e"를 배치한다. 이러한 방식으로 데이터를 제시하면 일반화를 쉽게 할 수 있다. 예를 들어, 일관된 순위를 가지기 위해서는 일부 W가 모든 L을 지배해야 한다. 브라조바누와 프린스(2005)는 주어진 논거에 필요한 충분한 조건을 달성하기 위해 퓨전이라고 알려진 과정과 데이터를 비교 표로 제시하는 다양한 방법을 설명한다.

예

간단한 예로서 영어 복수형의 발현을 고려한다.

/dɒɡ/ + /z/ → [dɒɡz](수치)
/kæt/ + /z/ → [kæts](수치)
/dɪʃ/ + /z/ → [dɪʃɪz](수치)

지배의 내림차순으로 다음과 같은 제약조건도 고려한다.

유형	이름	설명
표시성	*SS	두 개의 연속 시빌란트는 금지되어 있다. 출력물의 인접한 시빌란트 쌍에 대해 하나의 위반.
표시성	동의(음성)	출력부문은 [±음성] 규격에 동의한다. 음성이 일치하지 않는 출력 내 인접 장애물 쌍에 대한 하나의 위반.
충실함	맥스.	출력의 모든 입력 세그먼트 최대화 출력에 나타나지 않는 입력의 각 세그먼트에 대해 하나의 위반. 이 제약조건은 삭제를 방지한다.
	디프	출력 부문은 입력 통신원이 있느냐에 달려 있다. 입력에 나타나지 않는 출력의 각 세그먼트에 대해 하나의 위반. 이 제약조건은 삽입을 방지한다.
	식별자(음성)	[±음성] 규격의 정체성을 유지한다. 입력과 출력 간에 음성이 다른 세그먼트마다 하나의 위반.

/dɒɡ/ + /z/ → [dɒɡz]
/dɒɡ/ + /z/		동의하다	맥스.	디프	식별
a. ☞	드즈
b	dds.	*!			*
c	드즈			*!
d	dds.			*!	*
e	dɒɡ		*!

/kæt/ + /z/ → [kæts]
/kæt/ + /z/		동의하다	맥스.	디프	식별
a	kæz	*!
b. ☞	케츠				*
c	케츠			*!
d	æss.			*!	*
e	kæ		*!

/dɪʃ/ + /z/ → [dɪʃɪz]
/dɪʃ/ + /z/		*SS	동의하다	맥스.	디프	식별
a	드즈	*!	*
b	dds.	*!				*
c. ☞	드즈				*
d	dds.				*	*!
e	dɪʃ			*!

제약조건이 어떻게 재순번 되든 간에, 모든 종류의 [ss]는 항상 [zz]에게 질 것이다. 이것을 조화경계라고 한다. [dɒɡzz] 후보자에 의해 발생하는 위반행위는 [dɒ]s]에 의해 발생한 위반행위의 하위집합으로, 특히 모음의 어음을 인식한다면 형태소의 음성을 변경하는 것은 불필요한 제약조건 위반이다. /dɒɡ/ + /z/ tableau에는 어떠한 위반도 일으키지 않는 후보자[dɒɡz]가 있다. 문제의 제약조건 내에서 [dɒz]는 다른 모든 가능한 후보를 조화롭게 경계한다. 이는 다른 후보를 조화롭게 묶기 위해 후보가 승자가 될 필요가 없음을 보여준다.

위의 tableaux는 비교 tableaux 형식을 사용하여 아래와 같이 반복한다.

/dɒɡ/ + /z/ → [dɒɡz]
/dɒɡ/ + /z/	*SS	동의하다	맥스.	디프	식별
Dɒɡz ~ Dɒɡs	e	W	e	e	W
데즈 ~ 데즈	e	e	e	W	e
Dɒɡz ~ Dɒɡɪs	e	e	e	W	W
Dzz ~ Dɒɡ	e	e	W	e	e

/kæt/ + /z/ → [kæts]
/kæt/ + /z/	*SS	동의하다	맥스.	디프	식별
kæts ~ kæz	e	W	e	e	L
kæts ~ kætɪz	e	e	e	W	L
kæts ~ kæts	e	e	e	W	e
kæts ~ ktt	e	e	W	e	L

/dɪʃ/ + /z/ → [dɪʃɪz]
/dɪʃ/ + /z/	*SS	동의하다	맥스.	디프	식별
데즈 ~ 데즈	W	W	e	L	e
Dɪʃɪz ~ Dɪʃs	W	e	e	L	W
Dɪʃɪz ~ Dɪʃɪs	e	e	e	e	W
Dzz ~ Dɪʃ	e	e	W	L	e

/dɒɡ/ + /z/에 대한 비교 테이블au에서, 이러한 제약조건의 순위는 관측된 출력[dɒz]을 산출할 것이라는 것을 관찰할 수 있다. 패배자 선호 비교가 없기 때문에, [dzz]는 이러한 제약조건의 어떤 순위에서도 승리한다. 이는 이 입력에 기초하여 어떤 순위도 설정될 수 없다는 것을 의미한다.

/kæt/ + /z/의 테이블au에는 단일 W 및 단일 L의 행이 포함되어 있다. 이것은 동의, 최대, 그리고 디프가 모두 식별을 지배해야 한다는 것을 보여준다. 그러나, 이 입력에 기초하여 그러한 제약조건들 사이에 어떤 순위도 설정될 수 없다. 이 tableau를 기준으로 다음과 같은 순위가 설정되었다.

동의, Max, Dep ≫ Identification.

/dɪʃ/ + /z/에 대한 표는 원하는 결과를 예측하기 위해 몇 개의 순위가 더 필요하다는 것을 보여준다. 첫 번째 줄은 아무 말도 하지 않고, 첫 번째 줄에는 패배자 선호 비교가 없다. 두 번째 행은 [dɪɪz]와 [dɪʃz]의 비교를 근거로 *SS 또는 동의가 Dep를 지배해야 함을 나타낸다. 세 번째 행은 맥스가 Dep를 지배해야 한다는 것을 보여준다. 마지막 행은 *SS 또는 Identity가 Dep를 지배해야 함을 보여준다. /kæt/ + /z/ tableau로부터 Dep가 Ident를 지배한다는 것이 확립되었다. 이는 *SS가 Dep를 지배해야 한다는 것을 의미한다.

지금까지 다음과 같은 순위가 필요한 것으로 나타났다.

*SS, Max dep Dep ≫ ID

동의가 Dep를 지배할 수 있는 것은 가능하지만, 그럴 필요는 없다; 위에서 주어진 순위는 [ddʃɪz]가 나타나기에 충분하다.

표의 순위를 합치면 다음과 같은 순위 요약을 제공할 수 있다.

*SS, Max ≫ 동의, Dep ≫ ID

또는

*SS, Max, 동의서 ≫ DEP ID

순위를 선형적으로 작성할 때 동의서를 넣을 수 있는 두 개의 장소가 있다. 둘 중 어느 것도 정말로 정확하지 않다. 첫 번째는 *SS와 Max가 Associate를 지배해야 한다는 것을 암시하고, 두 번째는 Associate가 Dep를 지배해야 한다는 것을 암시한다. 이 두 가지 모두 진실하지 못하기 때문에 이렇게 선형적으로 순위를 작성하는데 실패하는 것이다. 이러한 종류의 문제들은 대부분의 언어학자들이 아래 나온 것처럼 필요하고도 충분한 순위를 나타내기 위해 격자 그래프를 사용하는 이유다.

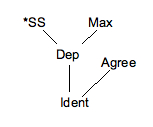
이 스타일에서 제약조건의 필수 순위를 나타내는 도표는 하세 도표다.

비판

Optimality 이론은 상당한 양의 비판을 끌어냈으며, 그 대부분은 음운론(구문이나 다른 분야보다는)에 응용하는 것에 초점을 맞추고 있다.^[16]^[17]^[18]^[19]^[20]^[21]

Optimality 이론은 음운론적 불투명성을 설명할 수 없다고 주장한다(예: Idsardi 2000 참조). 유도음운학에서는 표면 수준에서 설명할 수 없지만 "불투명한" 규칙 순서를 통해 설명할 수 있는 효과를 볼 수 있지만, 규칙이 작동하기 위한 중간 수준이 없는 최적성 이론에서는 이러한 효과를 설명하기 어렵다.

예를 들어, 퀘벡 프랑스어의 경우, 높은 전면 모음은 /t/, (예: /tipik/ → [tɪp]k])의 부착을 유발했지만, 높은 모음의 손실(표면 수준에서 볼 수 있음)은 명백한 원천이 없는 결합을 남겼다. 파생음운학에서는 모음시스코프(모음 손실) "반전" 결합 즉, 모음시스코프가 발생하고 "피어짐"(즉, 예방) 대신 모음시스코프 이전에 결합이 적용되어 높은 모음시스코프가 제거되고 발생된 환경이 파괴된다고 기술함으로써 이를 설명할 수 있다. 결속 따라서 그러한 역블레딩 규칙 순서는 표면 수준에서 효과가 보이지 않기 때문에 불투명(투명하지 않음)으로 불린다.

이론적 중간 형태에 접근할 수 없기 때문에(불투명성은 표면 형태 및/또는 기초 형태만 참조) 그러한 현상의 불투명성은 Optimality 이론에서 직접적인 설명을 찾지 못한다. 이를 설명하기 위해 고안된 여러 제안들이 있었지만, 대부분의 제안들은 Optimality 이론의 기본 구조를 현저하게 변화시켜, 따라서 크게 논란이 되는 경향이 있다. 이러한 변경은 종종 새로운 유형의 제약 조건(범용 충실도 또는 표시성 제약 조건이 아님)을 추가하거나 Gen의 속성(예: 직렬 파생 허용) 또는 Eval을 변경한다. 이것들의 예로는 존 J. 매카시의 동정론과 후보 사슬론을 들 수 있다.

관련 문제는 순환 체인 전환의 존재, 즉 입력 /X/가 출력[Y]에 매핑되지만 입력 /Y/가 출력[X]에 매핑되는 경우다. Optimality 이론의 많은 버전은 이것이 불가능하다고 예측한다(Moreton 2004, Prince 2007 참조).

Optimality 이론은 또한 언어 생산/인식의 불가능한 모델이라는 비판을 받고 있다: 무한한 수의 가능한 후보자들을 계산하고 비교하는 것은 처리하는데 무한히 오랜 시간이 걸릴 것이다. 다른 언어학자들이며, 최적성 이론의 보다 온건한 예시(Kornai(2006년 보)과 하인츠, Kobele & 그런 중요한 계산 문제도 제기하지 않는 이유로 이 주장은 Idsardi 제약 조건은 집합과 후보자들에 대해 터무니 없는. 가정을 만든다 분쟁 Idsardi(2006년),;Riggle(2009년))이 위치한다고 주장했다.. 이러한 최적성 이론의 비판에 대한 또 다른 일반적인 반박은 그 틀이 순수하게 대표적이라는 것이다. 이러한 관점에서 Optimality 이론은 언어 능력의 모델로 받아들여지고 따라서 언어 수행의 구체적인 사항을 설명하려는 의도는 아니다.^[22]^[23]

최적성 이론에 대한 또 다른 반대는 그것이 거짓으로 예측하지 않는다는 점에서 기술적으로 이론이 아니라는 것이다. 이 문제의 근원은 용어일 수 있다: 여기서 이론이라는 용어는 물리학, 화학 및 다른 과학에서와 다르게 사용된다. 최적성 이론의 특정 인스턴스화는 다른 언어 체계 내에서 특정 제안이 할 수 있는 것과 같은 방식으로 거짓으로 가능한 예측을 할 수 있다. 어떤 예측을 할 것인지, 그리고 그 예측이 시험 가능한지는 개별 제안의 구체적 내용에 달려 있다(가장 일반적으로 이것은 분석에 사용된 제약조건의 정의에 관한 문제다). 따라서 틀로서의 최적성 이론은 과학적 패러다임으로 가장^{[according to whom?]} 잘 묘사된다.^[24]