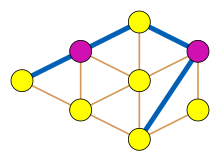
발톱이 없는 그래프

Claw-free graph
발톱

수학 영역인 그래프 이론에서 발톱 없는 그래프는 유도 하위그래프로 발톱이 없는 그래프다.

발톱은 완전한 초당적 그래프 K1,3(즉, 세 개의 가장자리, 세 개의 잎, 그리고 중심 꼭지점으로 구성된 별 그래프)의 다른 이름이다.집게가 없는 그래프는 유도 하위 그래프가 집게가 아닌, 즉 4개의 꼭지점 중 어떤 부분집합도 이 패턴에서 이들을 연결하는 세 개의 가장자리만 가지고 있다.마찬가지로, 집게가 없는 그래프는 어떤 꼭지점 근처가 삼각형이 없는 그래프의 보완인 그래프다.

집게 없는 그래프는 처음에 선 그래프의 일반화로 연구되었고, 그것들에 대한 세 가지 주요 발견을 통해 추가적인 동기부여를 얻었다: 짝수 순서의 모든 집게 없는 그래프들이 완벽하게 일치한다는 사실, 집게 없는 그래프에서 최대 독립 집합을 찾기 위한 다항 시간 알고리즘의 발견, 그리고 charac.발톱이 없는 완벽한 그래프의 [1]termination이들은 수백 개의 수학 연구 논문과 여러 설문 조사의 대상이다.[1]

예

정점과 가장자리가 발톱이 없는 그래프를 형성하는 다면체인 일반 이코사면체.
  • 어떤 그래프의 선 그래프 L(G)G;L(G)G의 모든 가장자리에 대한 꼭지점이 있고, 다른 가장자리 때문에 만일 세개의 가장자리 e1, e2, G에 e3 모두가 공유하는 엔드 포인트 e4 다음 우편함도 최소한 원칙적으로는 둘 때마다 해당 가장자리, G.A라인 그래프 L(G)에 있는 끝점이 발톱을 모시기에 공유하는 vertices L(G)에 바로 인접해 있claw-free 있다. e1의, e2 및 e는3 이러한 엔드포인트 중 하나를 서로 공유해야 한다.선 그래프는 9개의 금지된 하위 그래프로 특징지어질 수 있다;[2] 집게발은 이 9개의 그래프 중에서 가장 간단하다.이러한 특성화는 발톱이 없는 그래프를 연구하는 초기 동기를 제공했다.[1]
  • de Bruijn 그래프(일부 n의 경우 정점이 n비트 이진 문자열을 나타내고 가장자리가 (n - 1)비트가 두 문자열 사이에 겹치는 그래프)는 발톱이 없다.이를 보여주는 한 가지 방법은 (n - 1)비트 문자열에 대한 de Bruijn 그래프의 선 그래프로 n비트 문자열에 대한 de Bruijn 그래프를 구성하는 것이다.
  • 삼각형이 없는 그래프의 보완점은 발톱이 없다.[3]이 그래프들은 특별한 경우 전체 그래프를 포함한다.
  • 네 개의 적절히 교차하는 구간이 집단의 교차 그래프로 형성된 구간 그래프인 적절한 구간 그래프는 집게의 패턴에서 교차할 수 없기 때문에 집게가 없다.[3]적절한 원형 아크 그래프에서도 더 일반적으로 마찬가지다.[4]
  • 모저 스핀들(Moser Spindle)은 평면의 색수 하한을 제공하기 위해 사용되는 7Vertex 그래프로서, 발톱이 없다.
  • 여러 다면체 및 다면체의 그래프를 포함하여, 4면체 그래프와 더 일반적인 모든 단순체(완전한 그래프), 8면체 그래프 및 더 일반적인 교차 폴리토프(완전한 그래프에서 완벽한 일치를 제거하여 형성된 칵테일 파티 그래프에 대한 이형성), 정규의 그래프 등 여러 개의 다면체체체형 그래프에서 발톱이 없다.이코사헤드론,[5] 그리고 16세포의 그래프.
  • 슐레플리 그래프는 27개의 정점을 가진 강력하고 정규적인 그래프로서, 발톱이 없다.[5]

인식

정점의 각 4-튜플을 테스트하여 정점들이 집게를 유도하는지 여부를 확인함으로써 정점과 m 가장자리가 있는 주어진 그래프가 시간 O(n4)에 집게가 없는지 확인하는 것이 간단하다.[6]효율성이 높아지고 복잡성이 커지면 그래프의 각 꼭지점에 대해 인접 그래프의 보완 그래프에 삼각형이 포함되어 있지 않은지 확인하여 그래프의 집게 없는지를 테스트할 수 있다.그래프는 인접 행렬의 입방체가 0이 아닌 대각선 요소를 포함하는 경우에만 삼각형을 포함하므로, 삼각형을 찾는 것은 n × n 행렬 곱셈과 동일한 점근 시간 바인딩으로 수행될 수 있다.[7]따라서 Coppersmith-Winograd 알고리즘을 사용하여 이 집게 없는 인식 알고리즘의 총 시간은 O(n3.376)가 될 것이다.

클록스, 크래치 & 뮐러(2000년)는 어떤 발톱 없는 그래프에서 각 꼭지점에는 최대 2㎛의 이웃이 있다고 관찰한다. 그렇지 않으면 투란의 정리로는 정점 부근에 삼각 자유 그래프의 보완을 형성하기에 충분한 남은 가장자리가 없을 것이다.이 관찰을 통해 위에서 설명한 빠른 매트릭스 곱셈 기반 알고리즘의 각 근린 확인을 2㎛ × 2㎛ 매트릭스 곱셈과 동일한 점증 시간 범위로 수행하거나, 더 낮은 도수의 정점에 대해 더 빠르게 수행할 수 있다.이 알고리즘의 최악의 경우는 Ω((m) 정점들이 각각 Ω(mm)의 인접성을 가지고 있고, 나머지 정점들은 인접성이 거의 없기 때문에 총 시간은 O(m3.376/2) = O(m1.688)이다.

열거

발톱 없는 그래프에는 삼각형이 없는 그래프의 보완이 포함되기 때문에, n 정점에 있는 발톱 없는 그래프 수는 최소한 n의 제곱에서 기하급수적으로 삼각형이 없는 그래프의 수만큼 빠르게 증가한다.n = 1, 2, ...에 대한 n개 노드의 연결된 집게 없는 그래프 수는 다음과 같다.

1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184749, ... (시퀀스 A022562 in OEIS)

그래프의 연결을 끊을 수 있는 경우 그래프의 수는 훨씬 더 커진다.

1, 2, 4, 10, 26, 85, 302, 1285, 6170, ...(시퀀스 A086991 in OEIS).

Palmer, Read & Robinson(2002)의 기법은 이례적으로 그래프 열거 문제에 대해 발톱이 없는 입방 그래프의 수를 매우 효율적으로 계산할 수 있게 한다.

매치즈

짝수 순서의 집게가 없는 연결 그래프는 완벽한 일치를 가지고 있다는 섬너의 증거는 u로부터 가장 먼 두 개의 인접한 정점 v와 w를 제거하면 연결된 서브그래프가 남게 되는데, 그 안에서 동일한 제거 과정이 반복될 수 있다.

섬너(1974)와 독립적으로, 라스 베르기나스(1975)는 정점 수가 짝수인 모든 발톱 없는 연결 그래프가 완벽하게 일치한다는 것을 증명했다.[8]즉, 그래프에는 각 꼭지점이 정확히 일치하는 가장자리 중 하나의 끝점이 되도록 일련의 가장자리가 있다.선 그래프에 대한 이 결과의 특별한 경우는 짝수 수의 가장자리가 있는 그래프에서 가장자리를 길이 2의 경로로 분할할 수 있다는 것을 의미한다.완벽한 일치가 발톱 없는 그래프의 또 다른 특성화를 제공하는 데 사용될 수 있다. 즉, 그것들은 정확히 짝수 순서의 모든 연결된 유도 하위 그래프가 완벽한 일치를 갖는 그래프다.[8]

섬너의 증거는, 더 강하게, 연결된 집게가 없는 그래프에서, 한 쌍의 인접한 정점을 찾을 수 있고, 그 정점을 제거하면 나머지 그래프가 연결된 상태를 유지할 수 있다는 것을 보여준다.이를 보여주기 위해 섬너는 그래프에서 가능한 한 멀리 떨어져 있는 정점 u와 v의 쌍을 찾아 w를 가능한 한 u에서 멀리 있는 v의 이웃으로 선택한다. 그가 보여주는 것처럼 v와 w는 다른 노드에서 u까지의 어떤 최단 경로에도 놓여 있을 수 없으므로 v와 w의 제거는 연결된 채로 남겨둔다.이와 같은 방법으로 일치하는 쌍의 정점을 반복적으로 제거하면 주어진 집게 없는 그래프에서 완벽한 일치를 형성한다.

동일한 증명 아이디어는 만약 당신이 어떤 꼭지점이고, v는 u로부터 최대 멀리 있는 어떤 꼭지점이고, w는 u로부터 최대 멀리 있는 v의 어떤 이웃이다.또한 그래프에서 v와 w를 제거해도 u와의 다른 거리는 변경되지 않는다.따라서 u에서 최대한 멀리 떨어져 있는 쌍vw를 찾아 제거함으로써 일치를 형성하는 과정은 u에 뿌리를 두고 있는 그래프의 넓은 첫 번째 검색 트리의 단일 포스트오더 횡단에 의해 선형 시간 내에 수행될 수 있다.Chrobak, Naor & Novick(1989)은 같은 문제에 대한 효율적인 병렬 알고리즘뿐만 아니라 깊이 우선 검색에 기초한 대체 선형 시간 알고리즘을 제공한다.

그 다음을 포함한 Faudree, Flandrin &, Ryjáček(1997년)리스트 여러개의 관련 결과,:주문의(r1−)-connectedK1,r-free 그래프는 r≥ 2;이상한 주문의 최대 한개 degree-one 꼭지점claw-free 그래프는 특이한 주기와 그에 어울리는 분단 수도 있고 그것은 어떤 k에서 대부분의 절반의 최소 정도 o. 완벽한 matchings다f는 clak 또는 정점 수가 짝수인 w-free 그래프에는 k-through가 있고, cloe-free 그래프가 (2k + 1) 연결되면 어떤 k-edge 매칭도 완벽한 매칭으로 확장될 수 있다.

독립 집합

최대값이 아닌 독립 세트(보라색 노드 2개) 및 증가 경로

선 그래프의 독립형 집합은 기본 그래프에서 일치하는데, 두 개의 가장자리 집합 중 끝점을 공유하지 않는다.Edmonds(1965)의 Blooming 알고리즘은 다항식 시간에서 어떤 그래프에서든 최대 일치를 찾는데, 이것은 선 그래프에서 최대 독립 집합을 계산하는 것과 같다.이것은 Sbihi(1980)와 Minty(1980)에 의해 모든 발톱 없는 그래프에 대한 알고리즘으로 독립적으로 확장되었다.[9]

두 가지 접근법 모두 집게가 없는 그래프에서 정점은 독립된 집합에서 둘 이상의 이웃을 가질 수 없으며, 따라서 두 독립 집합의 대칭적 차이는 최대 두 개에서 정도(즉, 경로와 주기의 결합)의 하위 그래프를 유도해야 한다는 관측을 사용한다.특히, 내가 최대가 아닌 독립 집합인 경우, 그것은 짝수 사이클에 의한 어떤 최대 독립 집합과 다른 것으로서, 즉 I에서 정점이 아닌 정점과 I에서 정점 사이에 교대하는 유도 경로와 I에서 두 끝점 모두 I에서 이웃이 하나만 있는 유도 경로와 다르다.증가 경로에 대한 I의 대칭적 차이가 더 큰 독립 집합을 제공하므로 최대 일치 항목을 찾는 알고리즘에서와 유사하게 더 이상 찾을 수 없을 때까지 증가 경로 검색으로 작업이 감소한다.

스비히의 알고리즘은 에드몬드의 알고리즘의 꽃 수축 단계를 재현하고 유사하지만 더 복잡한 클릭 수축 단계를 추가한다.문제 인스턴스를 보조 선 그래프로 변환하고, 증분 경로를 찾기 위해 에드몬드의 알고리즘을 직접 사용하는 것이 민티의 접근법이다.나카무라 & 타무라 2001의 수정 후, 민티의 결과는 또한 다항 시간 내에 최대 중량의 독립된 집게를 찾는 일반적인 문제를 해결하는 데 사용될 수 있다.이러한 결과를 더 넓은 등급의 그래프로 일반화하는 것도 알려져 있다.[9]새로운 구조 정리를 보여줌으로써 Faenza, Oriolo & Stauffer(2011)는 큐빅 타임 알고리즘을 주었고, 이 알고리즘은 가중치 설정에서도 작용한다.

색칠, 패거리 및 지배

완벽한 그래프는 색수와 최대 클라이크의 크기가 동일하고, 이 균등이 유도된 모든 서브그래프에서 지속되는 그래프를 의미한다.완벽한 그래프가 홀수 사이클이나 홀수 사이클의 보완( 소위 홀수 홀수) 중 하나로 유도된 하위 그래프가 없는 그래프로 특징지어질 수 있다는 것이 현재 알려져 있다.[10]그러나, 수년 동안 이것은 여전히 풀리지 않은 추측으로 남아 있었으며, 오직 그래프의 특별한 하위 분류에서만 증명되었다.이러한 하위 클래스 중 하나는 발톱 없는 그래프 제품군이었는데, 여러 저자에 의해 발톱 없는 그래프가 홀수 사이클과 홀수 홀수 홀수 없이 완벽하다는 사실이 밝혀졌다.완벽한 발톱 없는 그래프는 다항식 시간에 인식될 수 있다.완벽한 발톱 없는 그래프에서, 정점 부근은 초당적 그래프의 보완점을 형성한다.완벽한 집게발 없는 그래프에 색상을 입히거나, 다항식 시간 내에 최대 집게를 찾을 수 있다.[11]

수학의 미해결 문제:

발톱이 없는 그래프에는 항상 목록 색도 번호가 색도 번호와 동일한가?

(수학에서 더 풀리지 않은 문제)

일반적으로 집게발 없는 그래프에서 가장 큰 집단을 찾는 것은 NP-hard이다.[12]또한 (선 그래프를 통해) 이 문제는 그래프의 색지수 계산의 NP-hard 문제를 일반화하기 때문에 그래프의 최적 색상을 찾는 것도 NP-hard이다.[6]같은 이유로 4/3 이상의 근사비를 달성하는 색소를 찾는 것은 NP-힘든 일이다.그러나 집게가 없는 그래프의 색수가 최대 도수의 절반 이상이기 때문에 탐욕스러운 색상 알고리즘을 통해 근사비를 2로 달성할 수 있다.가장자리 목록 색소 추측을 일반화하면, 발톱이 없는 그래프의 경우 목록 색소 번호는 색소 번호와 같으며, 이 두 숫자는 다른 종류의 그래프에서 멀리 떨어져 있을 수 있다.[13]

발톱이 없는 그래프는 χ 경계로, 큰 색수의 발톱이 없는 그래프마다 큰 클라이크가 포함되어 있다는 것을 의미한다.더욱 강하게, 큰 정도의 발톱 없는 그래프마다 그 정도의 제곱근에 대략 비례하는 크기의 큰 패거리가 들어 있다는 것은 램지의 정리로부터 따르게 된다.적어도 하나 이상의 3-Vertex 독립된 집합을 포함하는 연결된 집게 없는 그래프의 경우 색수와 클릭 크기 사이의 더 강한 관계가 가능하다. 이 그래프에는 색수의 절반 이상의 크기의 집단이 존재한다.[14]

모든 발톱 없는 그래프가 완벽한 것은 아니지만, 발톱 없는 그래프는 완벽함과 관련된 또 다른 속성을 만족시킨다.그래프는 독립된 최소 지배 집단을 가지고 있고 동일한 속성이 유도된 모든 하위 그래프에 포함된다면 지배완료라고 불린다.발톱이 없는 그래프에는 이러한 속성이 있다.이를 보려면 D를 발톱이 없는 그래프에서 지배적인 집합으로 하고, v와 w가 D에서 인접한 두 정점이라고 가정한다. 그러면 v가 지배하지만 w가 지배하지 않는 정점 집합은 클라이크여야 한다(엘세 v는 발톱의 중심이 될 것이다).만약 이 집단의 모든 꼭지점이 이미 D의 다른 구성원 한 명 이상에 의해 지배되고 있다면, v는 더 작은 독립적 지배 세트를 생산하면서 제거될 수 있고, 그렇지 않으면 v는 그 집단의 지배력이 없는 정점들 중 하나로 대체될 수 있다.이 교체 과정을 반복함으로써 결국 D보다 크지 않은 지배 세트에 도달하게 되므로, 특히 출발 세트 D가 최소 지배 세트일 때 이 프로세스는 똑같이 작은 독립적인 지배 세트를 형성한다.[15]

이러한 지배적 완벽성 특성에도 불구하고, 발톱이 없는 그래프에서 최소 지배력 설정의 크기를 결정하는 것은 NP-힘들다.[6]그러나, 더 일반적인 등급의 그래프와는 대조적으로, 집게가 없는 그래프에서 최소 지배 집합이나 최소 연결 지배 집합을 찾는 것은 고정 매개변수 추적가능하다. 즉, 지배적인 집합 크기의 지수 함수를 곱한 그래프 크기의 다항식으로 경계한 시간에 해결할 수 있다.[16]

구조

Chudnovsky &, 시모어는 그들이claw-free 그래프에 대한 구조체 이론,minor-closed 그래프 가족 로버트슨과 시모어에서 증명된 그래프 구조 정리, Chudnovsky, 시모어와 그들의 공동 저자의 강력한 perfe을 입증할 때 이러한 사용되는 완벽한 그래프에 대한 구조를 이론에 유사하다는 것을 증명한 서류 시리즈 개요(2005년).ct g랩 [10]정리그 이론은 여기서 자세히 설명하기에는 너무 복잡하지만, 그 맛을 내기 위해서는 그들의 결과 중 두 가지를 개략적으로 설명하기에 충분하다.첫째, 그들이 준선 그래프라고 부르는 발톱 없는 그래프의 특별한 하위 분류에 대해, 그들은 그러한 모든 그래프는 두 가지 형태 중 하나를 가지고 있다고 명시한다.

  1. 퍼지 원형 구간 그래프, 원의 점과 호로 기하학적으로 표현되는 그래프의 클래스로 적절한 원형 호 그래프를 일반화한다.
  2. 퍼지 선형 간격 그래프로 각 가장자리를 대체하여 다중 그래프로 구성된 그래프.이것은 여러 글자의 모든 가장자리가 꼭지점으로 대체되는 선 그래프의 구성을 일반화한다.퍼지 선형 구간 그래프는 퍼지 원형 구간 그래프와 같은 방식으로 구성되지만 원보다는 선에 생성된다.

추드노브스키와 세이모어는 임의로 연결된 발톱 없는 그래프를 다음 중 하나로 분류한다.

  1. 6가지 특정 등급의 발톱 없는 그래프.이 중 3개는 선 그래프, 적절한 원형 호 그래프, 그리고 이코사면체의 유도 하위 그래프들이다. 나머지 3개는 추가적인 정의를 포함한다.
  2. 그래프는 더 작은 발톱 없는 그래프에서 네 가지 간단한 방법으로 형성되었다.
  3. 반정점 그래프(Antirismatic graph)는 4개의 꼭지점마다 최소 2개의 가장자리가 있는 하위 그래프를 유도하는 집게 없는 그래프로 정의된다.

그들의 구조 이론에 있는 대부분의 작업은 항정신병 그래프의 추가 분석을 포함한다.Srg(27,16,10,8) 매개변수를 가진 집게가 없는 정규 그래프인 Schléfli 그래프는 분석의 이 부분에서 중요한 역할을 한다.이 구조 이론은 다면 결합기의 새로운 진보와 발톱 없는 그래프의 색도 수에 대한 새로운 한계뿐만 아니라 [5][17]발톱 없는 그래프에서 세트를 지배하기 위한 새로운 고정 매개변수-추적 알고리즘으로 이어졌다.[18]

메모들

  1. ^ a b c Faudree, Flandrin & Ryjahchek(1997), 페이지 88.
  2. ^ 베인케(1968년).
  3. ^ a b Faudree, Flandrin & Ryjahchek(1997), 89페이지.
  4. ^ 추드노브스키 & 시모어(2008).
  5. ^ a b c 추드노브스키 & 시모어(2005년).
  6. ^ a b c Faudree, Flandrin & Ryjahchek(1997), 페이지 132.
  7. ^ 이타이 & 로데 (1978년)
  8. ^ a b Faudree, Flandrin & Ryjahchek(1997), 페이지 120–124.
  9. ^ a b Faudree, Flandrin & Ryjahchek(1997), 페이지 133–134.
  10. ^ a b 추드노브스키 외 (2006).
  11. ^ Faudree, Flandrin & Ryjahchek(1997), 페이지 135–136.
  12. ^ Faudree, Flandrin & Ryjahchek(1997)는 132페이지에, 발톱이 없는 그래프에서 NP-hard의 NP-hardity는 폴작(1974)에 의해 입증된 NP-hard의 독립 세트 문제의 NP-hard에서 나온다고 관찰한다.
  13. ^ 그라비어 & 매프레이(2004년).
  14. ^ 추드노브스키 & 시모어(2010년).
  15. ^ Faudree, Flandrin & Ryjahchek(1997), 페이지 124–125.
  16. ^ Cygan 외 연구진(2011년)헤르멜린 외(2011년).
  17. ^ 킹& 리드(2015년).
  18. ^ 헤르멜린 외(2011년).

참조

  • Beineke, L. W. (1968), "Derived graphs of digraphs", in Sachs, H.; Voss, H.-J.; Walter, H.-J. (eds.), Beiträge zur Graphentheorie, Leipzig: Teubner, pp. 17–33.
  • Chrobak, 마레크;Naor, 조셉, 노빅, 마크 B(1989년),"효율적인 알고리즘의 설계에claw-free 그래프에 한정적 정도 신장 트리를 사용하여", Dehne, F.;약탈, J.-R.;산토로 N(eds.), 알고리즘 및 데이터 구조에:.워크숍 WADS 89, 오타와, 캐나다, 8월 1989년, 회보, 강의 노트 Comput에.Sci., 382vol., 베를린:스프링거,를 대신하여 서명함. 147–162, doi:10.1007/3-540-51542-9_13, hdl:1813/6891.
  • Chudnovsky, Maria; Robertson, Neil; Seymour, Paul; Thomas, Robin (2006), "The strong perfect graph theorem" (PDF), Annals of Mathematics, 164 (1): 51–229, arXiv:math/0212070, doi:10.4007/annals.2006.164.51, S2CID 119151552.
  • Chudnovsky, Maria; Seymour, Paul (2005), "The structure of claw-free graphs" (PDF), Surveys in combinatorics 2005, London Math. Soc. Lecture Note Ser., vol. 327, Cambridge: Cambridge Univ. Press, pp. 153–171, MR 2187738.
  • Chudnovsky, Maria; Seymour, Paul (2008), "Claw-free graphs. III. Circular interval graphs" (PDF), Journal of Combinatorial Theory, Series B, 98 (4): 812–834, doi:10.1016/j.jctb.2008.03.001, MR 2418774.
  • Chudnovsky, Maria; Seymour, Paul (2010), "Claw-free graphs VI. Colouring", Journal of Combinatorial Theory, Series B, 100 (6): 560–572, doi:10.1016/j.jctb.2010.04.005, MR 2718677.
  • Cygan, Marek; Philip, Geevarghese; Pilipczuk, Marcin; Pilipczuk, Michał; Wojtaszczyk, Jakub Onufry (2011), "Dominating set is fixed parameter tractable in claw-free graphs", Theoretical Computer Science, 412 (50): 6982–7000, arXiv:1011.6239, doi:10.1016/j.tcs.2011.09.010, MR 2894366, S2CID 16339210.
  • Edmonds, Jack (1965), "Paths, Trees and Flowers", Canadian Journal of Mathematics, 17: 449–467, doi:10.4153/CJM-1965-045-4, MR 0177907.
  • 파엔차:이탈리아 북부, 유리, Oriolo, 잔 파 올로, Stauffer, 고티에(2011년),"한 연산 분해 Claw-free Graphs의 가중 안정적인 설정 문제에 대한 O(n3)-algorithm 하게 해", 22회 ACM-SIAM 심포지엄 이산화 이론을 회보(PDF), SODA '11, 샌 프란시스코, 캘리포니아:SIAM,를 대신하여 서명함. 630–646,. doi:10.1137/1.9781611973082.49, S2CID 13353335.
  • Faudree, Ralph; Flandrin, Evelyne; Ryjáček, Zdeněk (1997), "Claw-free graphs — A survey", Discrete Mathematics, 164 (1–3): 87–147, doi:10.1016/S0012-365X(96)00045-3, MR 1432221.
  • Goldberg, Andrew V.; Karzanov, Alexander V. (1996), "Path problems in skew-symmetric graphs", Combinatorica, 16 (3): 353–382, doi:10.1007/BF01261321, S2CID 16308467.
  • Gravier, Sylvain; Maffray, Frédéric (2004), "On the choice number of claw-free perfect graphs", Discrete Mathematics, 276 (1–3): 211–218, doi:10.1016/S0012-365X(03)00292-9, MR 2046636.
  • Hermelin, 대니, Mnich, 마티아스, 밴 레이우엔, 에릭은 1월;Woeginger, 게르하르트(2011년),"통일 천하 때 별이 나오다", 자동자, 언어와 프로그래밍:38국제 콜로퀴움, ICALP 2011년 스위스 취리히, 7월 4-8 2011집, PartI, 강의 노트 컴퓨터 과학으로,. 462–473, 6755, 취리히, 스위스,를 대신하여 서명함 vol.. ArXiv:1012.0012, doi:10.1007/978-3-642-22006-7_39, S2CID 3080073.
  • Itai, Alon; Rodeh, Michael (1978), "Finding a minimum circuit in a graph", SIAM Journal on Computing, 7 (4): 413–423, doi:10.1137/0207033, MR 0508603.
  • King, Andrew D.; Reed, Bruce A. (2015), "Claw-free graphs, skeletal graphs, and a stronger conjecture on ω, Δ, and χ", Journal of Graph Theory, 78 (3): 157–194, arXiv:1212.3036, doi:10.1002/jgt.21797, S2CID 7385598.
  • Kloks, Ton; Kratsch, Dieter; Müller, Haiko (2000), "Finding and counting small induced subgraphs efficiently", Information Processing Letters, 74 (3–4): 115–121, doi:10.1016/S0020-0190(00)00047-8, MR 1761552.
  • Las Vergnas, M. (1975), "A note on matchings in graphs", Cahiers du Centre d'Études de Recherche Opérationnelle, 17 (2–3–4): 257–260, MR 0412042.
  • Minty, George J. (1980), "On maximal independent sets of vertices in claw-free graphs", Journal of Combinatorial Theory, Series B, 28 (3): 284–304, doi:10.1016/0095-8956(80)90074-X, MR 0579076.
  • Nakamura, Daishin; Tamura, Akihisa (2001), "A revision of Minty's algorithm for finding a maximum weighted stable set of a claw-free graph", Journal of the Operations Research Society of Japan, 44 (2): 194–204, doi:10.15807/jorsj.44.194.
  • Palmer, Edgar M.; Read, Ronald C.; Robinson, Robert W. (2002), "Counting claw-free cubic graphs" (PDF), SIAM Journal on Discrete Mathematics, 16 (1): 65–73, doi:10.1137/S0895480194274777, MR 1972075.
  • Poljak, Svatopluk (1974), "A note on stable sets and colorings of graphs", Commentationes Mathematicae Universitatis Carolinae, 15: 307–309, MR 0351881.
  • Sbihi, Najiba (1980), "Algorithme de recherche d'un stable de cardinalité maximum dans un graphe sans étoile", Discrete Mathematics, 29 (1): 53–76, doi:10.1016/0012-365X(90)90287-R, MR 0553650.
  • Sumner, David P. (1974), "Graphs with 1-factors", Proceedings of the American Mathematical Society, American Mathematical Society, 42 (1): 8–12, doi:10.2307/2039666, JSTOR 2039666, MR 0323648.

외부 링크